当前位置：文档之家 › 工程力学第4节 圆轴扭转时横截面上的应力

工程力学第4节 圆轴扭转时横截面上的应力

  • 格式：ppt
  • 大小：668.00 KB
  • 文档页数：6

下载文档原格式

  / 6

合集下载

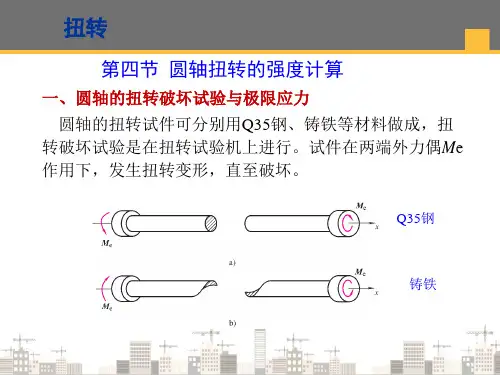
扭转—扭转轴的应力及强度计算(建筑力学)

扭转—扭转轴的应力及强度计算(建筑力学)
1.5 10 6


MPa 51.4MPa
4
WP
2.92 10
扭转
(2) 求空心轴的内径
因为要求实心轴和空心轴的扭转强度相同，故两轴的最
大切应力相等，即
'max max 51.4MPa

max
Tmax
Tmax


WP
D23 1 4 16


6
16Tmax
16
变形的能力。单位GPa，其数值可由试验测得。
切应变的其单位是 弧度（rad）
扭转
二、圆轴扭转时横截面上的应力
从几何关系、物理关系和静力学关系这三个方面来分析圆
轴受扭时横截面上的应力。
1. 几何变形方面
取一圆轴进行扭转试验
试验现象表明，圆轴表面上各点的变形与薄壁圆筒扭转
时的变形一样。
扭转
由观察到的现象，对圆轴内部的变形可做如下假设：扭转
截面（危险截面） 边缘点处。因此，强度条件也可写成 maxFra bibliotekTmax

[ ]
W
圆轴强度条件可以解决圆轴扭转时的三类强度问题，即
进行扭转强度校核、圆轴截面尺寸设计及确定许用荷载。
扭转
例9-6 一实心圆轴，承受的最大扭矩Tmax=1.5kN•m，轴
的直径d1=53mm。求：（1）该轴横截面上的最大切应力。
扭转
第四节 圆轴扭转的强度计算
一、圆轴的扭转破坏试验与极限应力
圆轴的扭转试件可分别用Q35钢、铸铁等材料做成，扭
转破坏试验是在扭转试验机上进行。试件在两端外力偶Me
作用下，发生扭转变形，直至破坏。
Q35钢
铸铁

材料力学-第4章圆轴扭转时的强度与刚度计算

材料力学-第4章圆轴扭转时的强度与刚度计算
B
I
C
A
II
D
III
I
II
III
M
x
0
确定各段圆轴内的扭 矩。
第4章 圆轴扭转时的强度与刚度计算
外加扭力矩、扭矩与扭矩图
3 ． 建立 Mx － x 坐 标系，画出扭矩图 建 立 Mx － x 坐 标 系，其中x轴平行于 圆轴的轴线，Mx轴垂 直于圆轴的轴线。将 所求得的各段的扭矩 值，标在 Mx － x 坐标 系中，得到相应的点 ，过这些点作x轴的 平行线，即得到所需 要的扭矩图。
P M e 9549 [N m] n
其中P为功率，单位为千瓦（kW）；n为轴的转速，单位为转/ 分（r/min）。 如果功率P的单位用马力（1马力=735.5 N•m/s），则
P[马力] M e 7024 [N m] n[r / min]
第4章 圆轴扭转时的强度与刚度计算
外加扭力矩、扭矩与扭矩图
第4章 圆轴扭转时的强度与刚度计算
工程中承受扭转的圆轴 外加扭力矩、扭矩与扭矩图 剪应力互等定理 剪切胡克定律
圆轴扭转时横截面上的剪应力分析 与强度设计 圆杆扭转时的变形及刚度条件 结论与讨论
第4章 圆轴扭转时的强度与刚度计算
工程中承受扭转的圆轴
第4章 圆轴扭转时的强度与刚度计算
绘出扭矩图：
第4章 圆轴扭转时的强度与刚度计算
B C
I
外加扭力矩、扭矩与扭矩图 A III D II
I 扭矩Mn-图
II
III
159.2
（+）
（-）
63.7 159.2
M n,max 159.2( N m)
（在CA段和AD段）

圆轴扭转横截面上的应力

圆轴扭转横截面上的应力
140 N.m，Ip= 3105 mm4，l = 2 m，G = 80 GPa，[] = 0.5 ()/m 。AC=? ，校核轴的刚度。
解：1. 变形分析
T1 MA 180 N m

AB

T1l GIp

1.5010-2
rad
T2 MC 140 N m
BC

T2l GIp
例 5-1 已知 T=1.5 kN . m，[ ] = 50 MPa，试根据强度条 件设计实心圆轴与 = 0.9 的空心圆轴，并进行比较。
解：1. 确定实心圆轴直径
max [ ]
max

T Wp

T πd 3
16
T πd
3

[
]
16
d
3

16T
π[ ]
3

16(1.5103Nm) π(50106Pa)
3. 计算支座约束力偶矩
联立求解方程 (a) 与 (b)
MA

Mb ， ab
MB

Ma ab
总结
• 圆轴扭转强度计算 • 圆轴扭转刚度计算
本章结束！

0.0535
m
取： d 54 mm
2. 确定空心圆轴内、外径
Wp

πdo3 16
14
16T [ ]
π 16
do3
(1

4)
do

3
16T
π(1 4)[
]

76.3
mm
di do 68.7mm
取：do 76 mm， di 68 mm 3. 重量比较

7-3圆轴扭转时的应力及强度条件

7-3圆轴扭转时的应力及强度条件
第三节
圆轴扭转时的应力及强 度条件
一、圆轴扭转时的应力
1、扭转变形 平面假设：圆周扭转变形后各个横截面仍为平 面，而且其大小、形状以及相邻两截面之间的 距离保持不变，横截面半径仍为直线。
推断结论：

横截面上各点无轴向变形，故 横截面上没有正应力。
横截面绕轴线发生了旋转式的 相对错动，故横截面上有剪应 力存在。 各横截面半径不变，所以剪应 力方向与截面径向垂直
解：传动轴的外力偶矩为：
P 80 M 9549 9549 1317.1N.m n 580
工作切应力的最大值：
3 T M 1317 . 1 10 3 39.58MPa [ ] 50MPa m ax 3 W p 0 . 2 d 0 . 2 55
强度足够！

带入数据后得：τ max＝50.33MPa<[τ ]＝60MPa;强度足够 2、设计实心轴直径D1（两轴的最大工作切应力相等) 3、两轴重量比 T T 2 G A L D m ax ；即 实心轴 1 1 3 2 W 0 .2D P G空心轴 A2 L D d 2 6 T 1 . 5 10 D3 3 53 .03 mm 532 0 .2 m ax 0.250 .3 2 3.21 2 90 85
6 T 5 10 AB 48 . 83 MPa AB max 3 W . 2 80 AB 0
6 T 1 . 8 10 BC 72 MPa BC max 3 W . 2 50 BC 0
二、圆轴扭转的强度条件
1、圆轴扭转的强度条件
纯扭圆轴横截面切应力分布
d1
A
解： 1.外力
C
M e2
d2

工程力学教案-圆轴扭转

工程力学教案-圆轴扭转

工程力学教案理、工科】4-1扭转的概念和实例工程上的轴是承受扭转变形的典型构件，如图4-1所示的攻丝丝锥，图4-2所示的桥式起重机的传动轴以及齿轮轴等。

扭转有如下特点：1.受力特点：在杆件两端垂直于杆轴线的平面作用一对大小相等，方向相反的外力偶■-扭转力偶。

其相应力分量称为扭矩。

图4-1攻锂2.变形特点横截面绕轴线发生相对转动，出现扭转变形。

假设杆件横截面上只存在扭矩这一个力分量那么这种受力形式称为纯扭转。

图42桥式起重机的传动轴■■§4-2扭矩扭矩图1.外力偶矩如图4-3所示的传动机构，通常外力偶矩用不是直接给出的，而是通过轴所传递的功=殖——〔KW 〕时有关系60，即率H 和转速n 计算得到的。

如轴在m 作用下匀速转动炉角，那么力偶做功为山=哪，由功率定义dAdN=——=m■—-=vn m dtdt角速度型(单位：弧度/秒，rad/s)与转速n (单位：转/分，r/min)的关系为①=?曲50。

因此功率N 的单位用千瓦恥=9550—(^'^(4-1a)式中："-传递功率〔千瓦，KW 〕，段-转速〔r/min 〕如果功率单位是马力(PS),由于1KW=1000N ・m/s=1.36PS,式〔4-1a 〕成为=7024—、(4-1b)式中："-传递功率〔马力，PS 〕 槪-转速〔r/min 〕2.扭矩求出外力偶矩用后，可进而用截面法求扭转力--扭矩。

如图4-4所示圆轴，由，从而可得A-A 截面上扭矩T7-^=0T=mF 称为截面A-A 上的扭矩；扭矩的正负号规定为：按右手螺旋法那么，T 矢量离开马力，从动轮B 、截面为正，指向截面为负。

或矢量与横截面外法线方向一致为正，反之为负。

【例4-4】传动轴如图4-5a 所示，主动轮A 输入功率虬 C 、D 输出功率分别为=马力，氏=20马力，轴的转速为ra=300r/mln 。

试画出轴的扭矩图。

Tin 凹(d)A —46S Nm©F7351hJm02Ntn图4-5【解】按外力偶矩公式计算出各轮上的外力偶矩叫=7024^=1170N'm=m c =7024^-=351N'm=7024^-=468Nm从受力情况看出，轴在BC ，CA ，AD 三段的扭矩各不相等。

工程力学-圆轴扭转变形分析

工程力学-圆轴扭转变形分析

P=7.5kW,轴的转速n=80r/min。试选择实心圆轴的直径d和空心圆轴的外
径d 2。己知空心圆轴的内外径之比=d 1/d 2=0.8,许用扭转切应力 [τ]=40MPa。
解：（1）外力偶矩为
M e 9550 7.5 N m 895 .3 N m 80
（2）扭矩为 T = Me = 895.3N· m （3）实心圆轴直径 根据强度条件
各点切应力的大小与该点到圆心的距离成正比，其分布 规律如图
圆轴扭转时，最大切应力 max 发生在圆轴表面。当ρ=R 时，其值为：
TR T max Ip IP / R
令 Wp
Ip R
max
T Wp
Wp称为扭转截面系数，它表示截面抵抗扭转破坏的能 力，单位是（mm）3。
工程中承受扭转的圆轴通常采用实心圆轴和空心圆轴两种形
max
T 16T 3 Wp πd
16 T 3 16 895.3 d 3 m 0.048m 48mm 6 [ ] 3.14 40 10
（4）空心圆轴外径
根据强度条件
max
T 16T 3 4 Wp πd 2 (1 )
16 T 16 895.3 3 d2 m 4 6 4 [ ](1 ) 3.14 40 10 (1 0.8 )
3
0.058m 58m m
内径d 1=α×d 2= 0.8×58 mm = 46.4mm
（5）比较重量
在长度相等、材料相同的情况下，空心圆轴与实心圆 轴重量之比等于横截面面积之比，即
四、圆轴扭转时的强度 计算
圆轴的扭转的强度条件
max
Tmax Wp

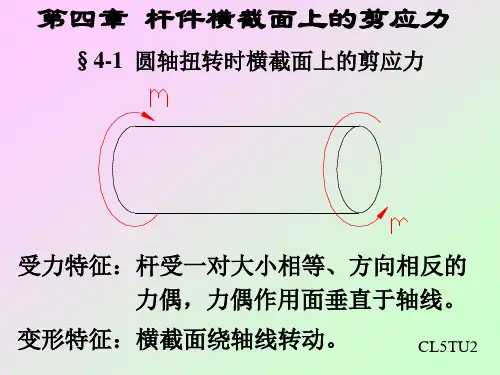
第四章杆件横截面上的剪应力(材料力学课件)

第四章杆件横截面上的剪应力(材料力学课件)

剪切胡克定律:


CL5TU8
薄壁圆筒的实验, 证实了剪应力与剪应变之间 存在着象拉压胡克定律类似的关系, 即当剪应力 不超过材料的剪切比例极限τp时,剪应力与剪应 变成正比
G
G称为材料的剪切弹性模量。上式关系称为剪切 胡克定律
剪切弹性模量G 材料常数：拉压弹性模量E
泊松比μ
对于各向同性材料,可以证明:E、G、μ 三个弹 性常数之间存在着如下关系:
CL5TU14
解：外管与内轴承受的扭矩相等，设为T
m
ml
Tl
Tl


G I p内 G I p内 G I p外
例：两端固定的圆截面等直杆AB，在截面 C受外力偶矩m作用，试求杆两端的支座反力 偶矩。
CL5TU15
解：
静力平衡方程为： mA mB m
变形协调条件为： AB AC CB 0
CL5TU12
解：
CV
AB a
Pal a GIp
32 Pa 2l
G d4
例：已知一直径d=50mm的钢制圆轴在扭
转角为 6°时，轴内最大剪应力等于90MPa，
G=80GPa。求该轴长度。
解： T l (1)
GIp
max

T Wt
(2)
(1) (2)
得：l
16
(1 4 )
二、圆轴扭转时的变形
d T
d x GI p
d T d x
GI p
T d x
l GI p
d
CL5TU5
若T const，则 T l
GIp l N l
EA
圆轴扭转时的强度条件和刚度条件

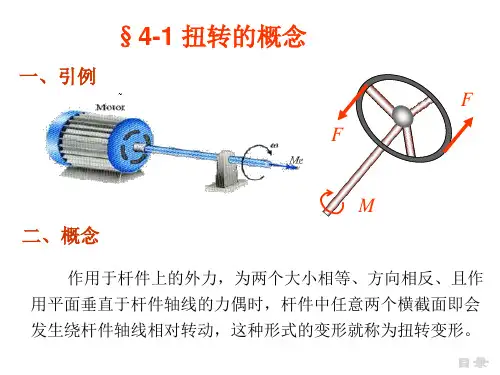
园轴扭转横截面上剪应力计算

园轴扭转横截面上剪应力计算

于是单元体abcd的ab边相对于cd也发生了微小的相对错 动，引起单元体abcd的剪切变形。
如图所示：ab边对cd 边相对错动的距离是：
m
n aa' Rd
d c
a
a
b
eR e
d
b
m
n
dx
e
e d
m
n
d c
a
a
b
eR e
d
b
m
n
dx
aa' R d 直角abc的角度改变量： ad dx
e
§4-1 扭转的概念
一、引例 F
F
M 二、概念
作用于杆件上的外力，为两个大小相等、方向相反、且作 用平面垂直于杆件轴线的力偶时，杆件中任意两个横截面即会 发生绕杆件轴线相对转动，这种形式的变形就称为扭转变形。
目录
• 受扭转构件的受力特点
——在垂直于杆轴的两平面内分别作用两个 等值，反向的力偶。 m m
处作用有载荷P。求：C点水平及铅垂位移
B
解：
a
A
C
aP a
C/
复习
§4-1 扭转的概念
1 扭转 2 轴
§4-2 外力偶矩的计算 扭矩和扭矩图
1 两个公式
2 扭矩的正负规定
§4-3 薄壁圆筒扭转时的应力 剪切虎克定律 1 应力计算方法和公式 2 剪切虎克定律公式 3 E G μ之间的关系
§4-4 圆轴扭转时的应力和强度条件
e d
—（a）
——圆截面a点处的剪应变，在垂直于半径oa的平面内。
同样道理：在距离圆心为处的剪应变为：
p
d
dx
—（b）
讨论：由图中可看出：（a）(b)两式中的

理论力学第四章扭转

理论力学第四章扭转
由 M x 0, T Me 0 得T＝M e
内力T称为截面n-n上的扭矩。
Me
Me
x T
Me
扭矩的符号规定：按右手螺旋法则判断。
右手的四指代表扭矩的旋转方向，大拇指代表其矢量方向，若 其矢量方向与截面的外法线方向相同，则扭矩规定为正值，反之为 负值。
+
T
-
扭矩图：表示沿杆件轴线各横截面上扭矩变化规律的图线。
4
32 7640180 80109 π 2 1
86.4 103 m 86.4mm
d1 86.4mm
4.直径d2的选取
按强度条件
A M e1 d1
B d2 C
M e2
M e3
3 16T 3 16 4580
②各纵向线均倾斜了同一微小角度 。
③所有矩形网格均歪斜成同样大小的平行四边形。
结论：
0, 0
横截面上
0 0
根据对称性可知切应力沿圆周均匀分布；
t D, 可认为切应力沿壁厚均匀分布, 且方向垂直于其半径方向。
t
D
微小矩形单元体如图所示：
①无正应力
②横截面上各点处，只产生垂 直于半径的均匀分布的剪应力
强度计算三方面：
① ②
校核强度：
max
Tm a x WP
设计截面尺寸：
WP
Tmax
[ ]
[ ]
Wt
实：D3 16 空：1D6（3 1 4）
③ 计算许可载荷： Tmax WP[ ]
例4.2 图示阶梯状圆轴，AB段直径 d1=120mm，BC段直径
d2=100mm 。扭转力偶矩 MA=22 kN•m， MB=36 kN•m， MC=14 kN•m。 材料的许用切应力[t ] = 80MPa ，试校核该轴 的强度。

圆轴扭转时的强度和刚度计算

圆轴扭转时的强度和刚度计算

A1 / A2 = [π (D 2 − d 2 ) / 4] /(πD 2 2 / 4) = (90 2 − 852 ) / 612 = 0.235
传动轴满足强度要求。 2)刚度校核 传动轴的极惯性矩为
I P = 0.1D 4 (1 − a 4 ) = {0.1 × 90 4 [1 − (85 / 90 ) 4 ]}mm 4 = 134 × 10 4 mm 4 θ max = 180 M n /(πGI P )
= (180 × 1500 × 10 3 / 80 × 10 3 × 134 × 10 4 π ) × 10 3 °/m
= 0.8°/m ＜ [θ ]
传动轴满足刚度要求。 (2)计算实心轴的直径
1)按强度条件设计(设直径为D1)。若实心轴与空心轴强 度相同，当材料相同时，它们的抗扭截面系数应相等，即
W n = πD 13 / 16 = πD 3 (1 Βιβλιοθήκη a 4 ) / 16由此得
D 1 = D3 1 − a 4 = [90 × 3 1 − (85 / 90) 4 ]mm = 53mm
根据扭转刚度条件，可以解决三类问题， 即校核刚度、 设计截面和确定许可载荷 。
例6-5 汽车传动轴AB由45号无缝钢管制成，外径D=90mm,
[ 内径d=85mm，许用切应力 [τ ]=60MPa，θ ] =1.0°/m，工作时最
大力偶矩M =1500N·m，G =80GPa。 (1)试校核其强度及刚度。 (2)若将AB轴改为实心轴，试求其直径。 (3)比较空心轴和实心轴的重量。 解 (1)试校核其强度及刚度。 1) 强度校核 传动轴各截面上的扭矩均为
θ max = 180M n /(πGI P ) ≤ [θ ]
(6-13)

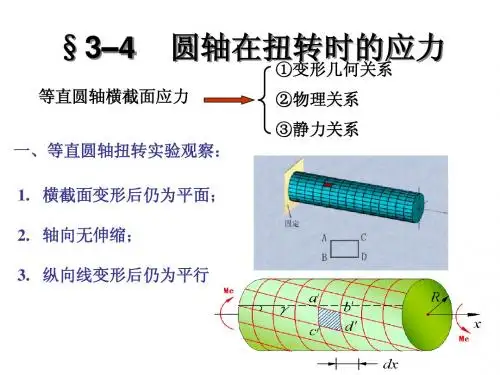
3–4 圆轴在扭转时的应力3-5 3-6 3-7

3–4 圆轴在扭转时的应力3-5 3-6 3-7

d1
l
(b)
d 2 D2
d13
16

3 D2 (1 4 )
l
16
D2 3 1 1.194 4 d1 1 0.8
§3–5 圆杆在扭转时的变形
一、扭转变形
1、圆轴扭转时的变形是用相对扭转角 来度量的
d T dx GI p
其中 d 代表相距为 dx 的两横截面间的相对扭转角。 长为 l 的一段杆两端面间的相对扭转角 可按下式计算
2
D 2 d 2


32 4 D 4 (1 ) 32
(D d )
4 4
d ( ) D
④ 应力分布
（实心圆截面）
（空心圆截面）
工程上采用空心截面构件：提高强度，节约材料，重量轻， 结构轻便，应用广泛。
⑤ 确定最大剪应力： 由
T Ip
知：当
d R , max 2
精确值：（修正公式，考虑弹簧曲率及剪力的影响）
max 4C 1 0.615 8DP K 8DP 4C 4 C d 3 d 3
D 其中： C 称为弹簧指数。 d 4C 1 0.615 K 称为曲度系数。 4C 4 C
弹簧丝的强度条件:
C
B
a
b
l
§3–6 圆柱形密圈螺旋弹簧的应力和变形
一、应力的计算
螺旋弹簧簧丝的轴线是一条空间螺旋 线，当螺旋角很小时（如小于5°）， 即可忽略其影响，认为簧丝的横截面 与弹簧的轴线在同一平面内，该种弹 簧称为密圈螺旋弹簧。当簧丝横截面 直径远小于弹簧圈的直径时，可近似 的用直杆公式计算。
T Q
=
Q
+

圆截面轴的扭转应力与变形

圆截面轴的扭转应力与变形

对应拉压问题 与轴力图
q
F 3ql
l
l/2 l/2
FN ql
x
2ql
Page 7
第四章 扭转
3. 轴的动力传递
已知传动构件的转速与所传递的 功率，计算轴所承受的扭力矩。
电机
联轴器
A
B
P M
角速度 2 n
60
n : 转速 (r min) 功率：KW 力偶矩：N.m
P 103 M 2 n
60
T1 ( x)
ml
2ml
在AB、BC和CD段分别由三截面 x 切开，考察左（或右）段平衡
D
AB段： T1 x mx
BC段： T2 ml
CD段： T3 2ml
画扭矩图
x
•试与轴力图比较，
考察对应关系。
Page 6
2.扭矩图对应的轴力图
M 3ml
m
A
B
C
D
l
l/2 l/2
T ml
x
2ml
第四章 扭转
R1
R2
O
T
空心轴
O
T
IP
空心圆能用？
思考:同样横截面积S的实心圆与空心圆,哪个强度性能好
实心圆 S D02
4
D 4S
空心圆
D2(12 )
S
4
4S D
12
Page23
实心圆 空心圆
D0
4S
D
4S
1 2
实心圆
Wp
D03
16
S
空心圆 Wp
4 D0
Wp S (1 2 )D
4
第四章 扭转
三、圆轴合理截面与减缓应力集中

圆轴纯扭转时横截面上的正应力研究

圆轴纯扭转时横截面上的正应力研究

0. 34
40. 0
130
1. 62
0. 85
乙烯塑料
0. 35
3. 5
30
0. 47
1. 56
混凝土
0. 17
18. 0
26
0. 05
0. 20
聚碳酸酯
0. 50
4. 0
50
1. 41
2. 81
·28 ·
集美大学学报 (自然科学版)
第6卷
2 结论
1) 圆轴扭转时 , 横截面上确实存在正应力 , 对于各向同性材料 , 横截面上的最大正应 力与同截面上的最大剪应力的平方成正比 , 而与材料的纵弹性模量 E 成反比.
集美大学学报 (自然科学版)
Journal of Jimei University(Natural Science)
[ 文章编号 ] 1007 - 7405 (2001) 01 - 0025 - 04
Vol. 6 No. 1 Mar. 2001
圆轴纯扭转时横截面上的正应力研究
张晓明
(集美大学机械工程学院 , 福建 厦门 361021)
文章编号1007740520010104圆轴纯扭转时横截面上的正应力研究集美大学机械工程学院福建厦门361021摘要以平面假设为基础分析圆轴扭转时横截面上的正应力分布以及最大正应力与最大剪应力的相对比值的影响因素并对强度计算时是否必须考虑扭转正应力提供了判断依据
第 6 卷 第 1 期
2001 年 3 月
规律如图 (3) 所示. 在圆轴周边上
各点拉应力最大 , 而在轴心压应力
最大.
(σ′) max = Eτ2max/ 4 G2 (σ′) mim = - Eτ2max/ 4 G2 (12)

讨论圆轴扭转时的应力状态

讨论圆轴扭转时的应力状态

130一、讨论圆轴扭转时的应力状态，并分析铸铁试件受扭时的破坏现象。

解 根据第十九章讨论，圆轴扭转时，在横截面的边缘处剪应力最大，其数值为:n n W M=τ (e )在圆轴的最外层，按图22-5(a )，所示方式取出单元体ABCD ，单元体各面上的应力如图22-5(b )所示。

在这种情况下，ττσσ===xy y x ，0 （f ）单元体侧面上只有剪应力作用，而无正应力作用的这种应力状态称为纯剪切应力状态。

把(f )式代入公式(22-6)得:min maxσσ ττσσσσ±=+-±+=22)2(2xy y x y x 由公式（22-5）：yx xytg σστα--=220 →∞-所以 2709020--=或α450-=α 或 1350-=α以上结果表明，从x 轴量起，由 450-=α(顺时针方向)所确定的主平面上的主应力为max σ；而由 1350-=α所确定的主平面上的主应力为min σ。

按照主应力的记号规定：τσσστσσ-=====min 32max 10所以，纯剪切是二向应力状态，两个主应力的绝对值相等，都等于剪应力τ，但一个为拉应力，一个为压应力。

圆截面铸铁试件扭转时，表面各点max σ所在的主平面联成倾角为︒45的螺旋面[图22-5（a ）]。

由于铸铁抗拉强度较低，试件将沿这一螺旋面因拉伸而发生断裂破坏，如(a )(c ) 图22-5131图22-5（c ）所示。

二、 图22-6（a ）所示为一横力弯曲下的梁，求得截面m －n 上的弯矩M 及剪力Q 后，算出截面上一点A 处弯曲正应力和剪应力分别为：MPa MPa 50,70=-=τσ[图22-6（b ）]试确定A 点处的主应力及主平面的方位，并讨论同一横截面上其它点处的应力状态。

解 把从A 点处截取的单元体放大如图22-6（c ）所示。

选定x 轴的方向垂直向上，则0=x σ MPa y 70-=σ MPa xy 50-=τ由公式（22-5）得： 429.1)70(0)50(2220=----=--=yx xytg σστα︒=5520α或︒235 ︒=5.270α或︒5.117从x 轴量起，按逆时针方向量取的角度︒5.27，确定max σ所在主平面，以同一方向量取的角度,5.117︒确定min σ所在的另一主平面。

精编工程力学教学课件 第4章 扭转

精编工程力学教学课件 第4章 扭转

6 103 0.083 1 (3
16 87.3106 Pa 4)4

4
D02

762 682 542
0.395
§4. 5 圆轴扭转时的变形和刚度条件
一、扭转角的计算
转第
4 章
扭
由上节知
T

GI P
d
dx
，所以 d T dx ，于是
GI P



d


T GI
P
dx
对于扭矩为常数的等截面圆轴，扭转角为
Tl
GI P 称为截面的抗扭刚度。
GI P
内径d2=60mm，外径D=80mm，所受外力偶矩如图。各
段杆的容许剪应力为 100 MPa 。（1）试校核该轴的
强度；（2）如材料的剪切弹性模量 G 8104 MPa ，求
此轴总扭转角。
解：（1）作扭矩图如图 所示。
4kNm 10kN m
A
BC
6kN m D
（2）强度校核
布可视作均匀的，切应力沿圆周切
线，方向与扭矩转向一致。 MK
（1）横截面上只有剪应力， 没有正应力；（2）剪应力的方向 沿圆周的切线方向。

r
MK

x
§4.3 薄壁圆管的扭转
A dA r0 T
转第
4
r0 AdA r0 2 r0 t T
该定理具有普遍性，不仅对纯剪切应力状态下成立，对 正应力和剪应力同时作用的单元体亦成立。
§4. 3 薄壁圆管的扭转
三、剪切虎克定律
´
转第
单元体ab 的倾角 称为切应变，
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。


T WP
三、圆截面极惯性矩 及抗扭截面模数
实心圆截面
d
IP A 2dA 02 2 2 d
d 4
32
WP

D3
16
空心圆截面
O d
D
令内外径比为 =d/D，则有：
Ip

D/2
d/2
2 2
d
D4 (1 4 )
32
WP

D3
16
2、物理关系
剪切胡克定律 G
各点的切应力


G

G
d
dx
3、静力关系
dA

R

dA
取dA为距截面中心 处的微面积，则dA为作
用在微面积上的力dA对截面中心之距，整个横截面
上这些力矩的合成结果应等于扭矩T：
横截面积
T

A

dA

AG 2
d
dx
dA

G
d
dx
A

2dA
T

G
d
dx
A
2dA
极惯性矩 IP A 2dA
则得： TFra bibliotekGIP
d
dx
物理关系式 比较


G
d
dx


T
IP
等直圆轴扭转时横截面上 任一点处切应力的计算公式
二、最大扭转切应力
max

TR IP
令 WP IP / R 称为抗扭截面模数

max
一、扭转切应力的一般公式
1、变形的几何关系 试验观测：取一易变形的 圆形截面直杆，在此圆轴 的表面各画几条相平行的 圆周线和纵向线；在轴的 两端施加一对力偶矩 M 使 其产生扭转变形。
观测结果
1）圆周线的形状和大小不变，两相邻圆周线的间距 保持不变，仅绕轴线作相对转动。
2）纵向线均倾斜了一个角度 。
平面截面假设：圆轴扭转变形后，横截面仍保持为 平面，且其形状大小不变，横截面上的半径仍保持 为直线，即横截面刚性地绕轴线作相对转动。
圆轴扭转时横截面上 的应力关系


tan

AA KA

R
d
dx
K
A A'
LB B'


tan

BB LB


d
dx
d/dx=/R，所以在同一横截面上d/dx是一个常数， 因此各点的切应变与该点到圆心的距离 成正比。
D4
Pa
5.84 MP
32

max

T WP

T
D3

742
0.060 3
Pa
17.5 MP
16
16
(1 4 )
例7-3 已知实心轴的直径 D 60 mm，轴的转速 n 450 r/min，传递的功率 P 35 kW，试求：距圆
心为 10 mm处的切应力，以及最大切应力。
解：1）计算外力偶矩
T

MA
9550
P n
742 N m


T
IP

74210103