线性系统理论(参考答案)(1)

R C 2《线性系统理论》试卷及答案1、（20分）如图所示RLC 网络,若e(t ）为系统输入变量r （t)，电阻R 2两端的电压为输出量y(t),选定状态变量为 x 1（t)=v 1（t ），x 2(t ）=v 2(t)，x 3（t)=i （t)要求列写出系统的状态空间描述。

2、(15分)求出下面的输入输出描述的一个状态空间描述。

y （4)+4y （3）+3y （2）+7y （1）+3y=u (3）+ 2u （1）+ 3u3、（15分）计算下列线性系统的传递函数。

[]210X 13101X y -⎡⎤⎡⎤=+⎢⎥⎢⎥-⎣⎦⎣⎦=4、(10分）分析下列系统的能控性.0111X X u a b •⎡⎤⎡⎤=+⎢⎥⎢⎥-⎣⎦⎣⎦5、（10分）分析下列系统的能观性。

[]1110a X X y Xb •⎡⎤==-⎢⎥⎣⎦6、（15分)判断下列系统的原点平衡状态x e 是否大范围渐近稳定。

12221123x x x x x x==--7、（15分）已知系统的状态方程为221012000401X X u •--⎡⎤⎡⎤⎢⎥⎢⎥=-+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦试确定一个状态反馈阵K,使闭环极点配置为λ1*=—2、λ2*=-3、λ3*=—4.答案：1、（20分）如图所示RLC 网络，若e （t ）为系统输入变量r （t ）,电阻R 2两端的电压为输出量y （t ），选定状态变量为 x 1(t)=v 1（t)，x 2(t ）=v 2（t ）,x 3（t)=i （t ）要求列写出系统的状态空间描述。

2、（15分）求出下面的输入输出描述的一个状态空间描述。

列出向量表示形式解出解出解出r x x x L R x x x rx LR x x x xx x C R x x x C xC x r x R x L L LL⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+--=-=+=+==++1321113211311132122222112211333113000xy x xLy （4）+4y (3）+3y （2)+7y (1）+3y=u （3）+ 2u （1)+ 3u[]得出了状态空间表达式列出向量表示形式，就求导，有选取状态变量令有令⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=++=⎪⎪⎩⎪⎪⎨⎧+----=========⎩⎨⎧++==++++++++=++++++===43211025233375y ~y ~x y ~x y ~...y ~x y ~x y ~3y ~2y ~y ~3y ~7y ~3y ~4y ~u 3734p 1y ~3734p 32p y d/dtp 4214321(4)43(2)22(1)1(3)4(1)21(1)(3)(1)(2)(3)(4)2342343x x x x x x x y u x x x x x x x x y u p p p u p p p p(完整word 版)《线性系统理论》试卷及答案3、(15分）计算下列线性系统的传递函数.[]Xy u X 10103112X =⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=[][][]计算得出传递函数⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-------=-=⎥⎦⎤⎢⎣⎡-------=⎥⎦⎤⎢⎣⎡--=--==⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡--==⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=----1021131)3)(2(110)()(21131)3)(2(13112)()()(1010311210103112X 1111s s s s B A Is C s G s s s s s s A Is BA Is C s G CB A Xy u X(完整word 版)《线性系统理论》试卷及答案4、（10分）分析下列系统的能控性。

x&1 x&2
=
−7
0
x&3 0
0 −5 0
0 x1 0
0
x2
+
4
−1 x3 7
0
0 5
u1 u2
解：由于对角规范型中 B 包含元素全为零的行，故系统不完全能控。
3．（约当规范形判据的应用）判断下面系统的能控性和能观性
1 1 0 0 0 1
x&
=
0 0
1 0
0 1
u = e(t)，输出变量 y = uc。
解：
e
=
uc
+
R
⋅C
duc dt
, x& = − 1 x + 1 u RC RC
, y=x
2．(由输入输出描述建立状态空间描述)系统的传递函数如下，求系统的状态空 间描述
G(s)
=
s3
s2 + s + 5 + 6 s2 + 12 s
+
4
0 解：可控标准形， x& = 0
s −1 0 1 det(sI − A) = 0 s −1 0 = (s −1)2 (s − 2) = 0
0 0 s−2
则系统特征值为 λ1 = 1（ λ1 的代数重数 σ1 = 2 ）， λ2 = 2 （ λ2 的代数重数 σ 2 = 1 ）。 （2）有重特征值，判断是否可以化为对角规范形
对于 2 重特征值 λ1 = 1，它所对应的特征矩阵
1 0
υ11
= 1,υ22
= 1 ，得到
2
个属于二重特征值 λ1
= 1的特征向量υ1
=
0

若 li 是 A 的特征值，试证 [1 li li 2 li n -1 ]T 是属于 li 的特征向量。 1—2 若 li 是 A 的一个特征值，试证 f (li ) 是矩阵函数 f (A) 的一个特征值。 1—3 试求下列矩阵的特征多项式和最小多项式
é l1 1 0 0 ù ê ú ê 0 l1 1 0 ú ê ú ê ú ê 0 0 l1 0 ú ê ú ê 0 0 0 l1 ú ë û é l1 1 0 0 ù ê ú ê 0 l1 0 0 ú ê ú ê ú ê 0 0 l1 0 ú ê ú ê 0 0 0 l1 ú ë û é l1 1 0 0 ù ê ú ê 0 l1 0 0 ú ê ú ê ú ê 0 0 l1 1 ú ê ú ê 0 0 0 l1 ú ë û
y =
t
ò0 g(t - t )u(t )d t
若脉冲响应 g 由图 1—12(a)给定。试问，由图 1—12(b)所示的输入而激励的输出为何？ g(t) 1 1 (a) 图 1—12 脉冲响应和输入作用 1—12 试求图 1—13 所示系统的动态方程式(略)
29
u(t) 1 2 t 1 2 (b) t
n >m
试证，给定初始状态 x(m ) = x0 下，时刻 n 的状态为 x(n )=F(n, m )x(0) 。若 A 与 n 无关，则
F(n, m ) 为何？
1—27 证明 x(n + 1) = A(n )x(n ) + B(n )u(n ) 的解为
n -1
x(n ) = F(n, m )x(m ) +
1 ù ú s+3ú 5s + 1 úú s + 2 úû
的实现，并画出其模拟图。 1—25 设{ A , B , C , D }和{ A , B , C , D }是两个线性时不变系统，其维数不一定相同。证明当 且仅当

2．(根据框图写出状态空间描述) 图2.2中描述了列车悬浮系统的工作原理，其中，1、2、3、 4为电磁装置，车辆通过电磁力的作用，悬浮于轨道上。磁悬浮控制系统的目的是通过调整 电磁作用力的输入，保证列车在运行过程中的平稳。这里我们考虑车辆运行过程中产在x和y 轴两个方向的位移，给出其线形化系统框图如图2.1所示
描述，其中g 是重力加速度常数，如图3所示，h 是自行车质心距地面高度，w 是两个轮子 与地面接触点的距离， b 是自行车质心投影与后轮和地面接触点的距离。 试给出该线性系统 的一个状态空间描述。
图3 参考文献： [3.1] Bicycles, motorcycles, and models-single-track vechicle modeling and control, IEEE Control Systems Magazine, October, 2006. 参考解答：
作业一
1．（线性化）已知倒立摆系统满足如下非线性状态方程
1 (t ) x2 (t ) x 2 (t ) ( g / l ) sin x1 (t ) u (t ) x
通过线性化给出系统在平衡解 [ x1 (), x2 ()] [0,0] ， u () 0 的邻域内的线性模型。 参考解答：
图 2.2
参考解答：
注意状态变量的维数. 3． （从传递函数得到状态方程描述）图3中给出了解释自行车姿态动态平衡的原理图示。在 前进速度保持为定常v 的假设下，车把转角 对车身姿态角 的作用在平衡点（ ＝0， ＝0）附近范围内可用微分方程

g v2 bv h hw wh
图2.1 这里A11=[100 0；0 200] B21=[10 -3；-5 16] C22=[1 1；1 -1]。 这里输入向量u是控制的作用力， 也就是车辆的加速度量， 输出向量y是车辆在两个轴方向的 位移量，通过间隙传感器测量。试列写出系统的状态空间模型。 参考文献： [2.1] H2 and H∞ control for MagLev vehicles，IEEE Control System Magazine, 1998 [2.2] Experimental comparison of linear and nonlinear controllers for a magnetic suspension, Proceedings of the 2000 IEEE International Conference on Control Applications，2000 [2.3] 广义线性磁悬浮对象的H∞控制问题，西安交通大学学报，Feb，2000

⎡ − 1 1 0⎤ ⎥ =⎢ ⎢ 0 − 1 1⎥ ⎢ 1 1⎥ ⎣1 ⎦
T ⎡ s3 ⎤ ⎡− 2 − 1 1⎤ ⎢ T ⎥ 1⎢ P = ⎢ s3 A ⎥ = ⎢ 1 − 1 1⎥ ⎥ 3 ቤተ መጻሕፍቲ ባይዱ 2⎥ ⎢ s3 ⎢ ⎥ A 1 2 1 ⎣ ⎦ ⎣ ⎦
P
−1
A = PAP
9－13
−1
⎡0 1 0 ⎤ ⎥ =⎢ ⎢0 0 1 ⎥ ⎢ ⎣1 0 0 ⎥ ⎦
由约当形可控性判据知系统不可控，因为特征值 λ1 对应两个约当块。
4
9－9
若 R,T 可逆，试证明分块矩阵的下列恒等式
⎡R M ⎤ ⎢0 T ⎥ ⎣ ⎦
证明
−1
⎡ R −1 =⎢ ⎣ 0
− R −1 MT −1 ⎤ ⎥ T −1 ⎦
− R −1 MT −1 ⎤ ⎡ R M ⎤ ⎡ I 0⎤ ⎥×⎢ ⎥=⎢ ⎥ T− ⎦ ⎣ 0 T ⎦ ⎣0 I ⎦
2
③可控性矩阵为
3
S= b
[
Ab
⎡0 1 − 1⎤ ⎥ A b =⎢ ⎢1 − 1 0 ⎥ ⎢ 1⎥ ⎣1 1 ⎦
2
]
rankS = 3
−1
可控
0 ⎤ ⎡s − 1 −1 ⎢ G ( s ) = c(sI − A) b = [1 0 1]⎢1 s + 1 0 ⎥ ⎥ ⎢ ⎥ s − 0 0 1 ⎣ ⎦
& = Ax + bi u x
⎡ − 2 2 − 1⎤ A= ⎢ 0 −2 0 ⎥ ⎢ ⎥ 1 − 4 0 ⎢ ⎥ ⎣ ⎦
试判定 [ A , 解
（ i = 1,2,3 ）
⎡0⎤ b1 = ⎢0⎥ ⎢ ⎥ ⎢ ⎣1 ⎥ ⎦
⎡0⎤ b2 = ⎢ 1 ⎥ ⎢ ⎥ ⎢ ⎣0⎥ ⎦

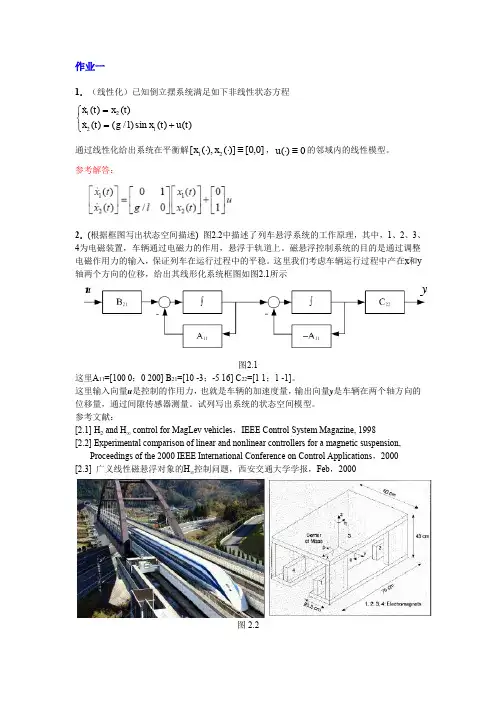
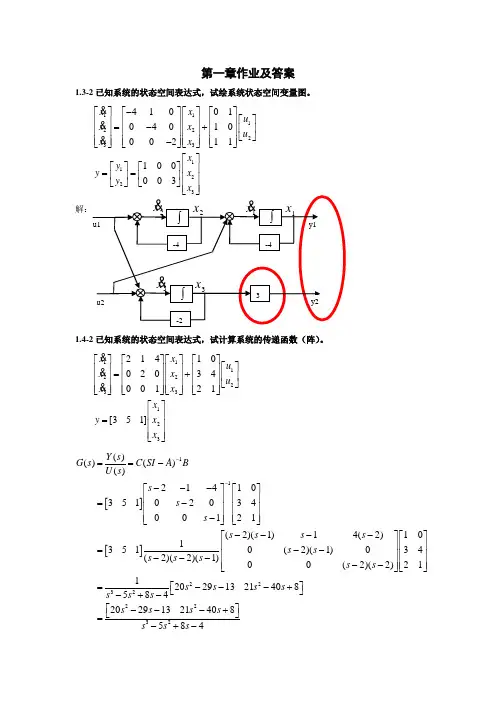
第一章作业及答案1.3-2已知系统的状态空间表达式，试绘系统状态空间变量图。

11122233112241001040100021110003xx u x x u x x x y y x y -⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=-+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎣⎦⎡⎤⎡⎤⎡⎤⎢⎥==⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦1.4-2已知系统的状态空间表达式，试计算系统的传递函数（阵）。

11122233123214100203400121[351]xx u x x u x x x y x x ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦[][]112232()()()()21410351020340121(2)(1)14(2)1013510(2)(1)034(2)(2)(1)00(2)(2)21120291321408584Y s G s C SI A B U s s s s s s s s s s s s s s s s s s s s s s --==----⎡⎤⎡⎤⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦----⎡⎤⎡⎤⎢⎥⎢⎥=--⎢⎥⎢⎥---⎢⎥⎢⎥--⎣⎦⎣⎦⎡⎤=---+⎣⎦-+-223220291321408584s s s s s s s ⎡⎤---+⎣⎦=-+-注意：也可写做[][][]23220212940138584s s s s s +--+--+-1.5-1已知系统传递函数，试用传递函数求出系统的状态空间模型。

2()35()()(3)(2)Y s s G s U s s s +==++解：通过赋予研究对象不同的内部结构可将传递函数转换成不同的状态空间模型。

（1）求出上述传递函数能控标准型表示由已知条件可知该传递函数为严格真分式，且该系统为单入单出（SISO ）三阶系统。

根据公式10111()...(),(1)()...mm mn n nY s b s b s b G s n m U s s a sa --+++===++++其中，可将传递函数写为223235035()(3)(2)82118s s s G s s s s s s +++==+++++其中，123012a 8,21,18,0,3,5a a b b b ======。

x 11 e t x 21 , 21 0 , x
x11 ( t 0 ) 1 x 21 ( t 0 ) 0
，
x 12 e t x 22 , 22 0 , x
x12 ( t 0 ) 0 x 22 ( t 0 ) 1
解得
x12 e t e t 0 x11 1 ， x 21 0 x 21 1 1 (t ) x 0 e
( sI A )
1
s ( s 1) 0 2 det( sI A ) s ( s 1) 0 adj ( sI A ) 1
s 1 ( s 1) 0
2
s ( s 1) 1 s ( s 1) 1 s 1 1
2
所以 e
。
可以看出， f ( i ) 是 f ( A ) 的一个特征值。
1-3 解：(1) 特征多项式为 1 ( ) ( 1 ) .
4
验证
A 1 I 0 , ( A 1 I ) 2 0 , ( A 1 I ) 3 0 , ( A 1 I ) 4 0
At
e t 1 1 L [( sI A ) ] 0 0
e 1 1 0
t
t t 1 e te t e 1 。 t e
1-5 证明：因为 D 1 存在，所以由 D R p p
A det C B IA det D 0 BD A I D C
c
k 0
k
A
k
设 x 是属于 i 的一个非零特征向量，故
A x i x
.
2 2 因此 A x A Ax A i x i Ax i i x i x .

2-17 证明：①首先证明()T T T B C A ，，是()s G 的不可简约实现（该题有问题，不是()TT TCB A，，）。

由于()s G 是对称传递函数阵，故有()()T T T C sI B B A sI C 1-1-A --=，所以()TT TBC A，，是()s G 的实现。

又因为()[]n CA CA Crank CA C A C rank n Tn TT T T =⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=1-1- ，其可控； 同理可证其可观，故系统()T T T B C A ，，是可控可观的。

所以其是()s G 的不可简约实现。

②证明P 的对称性。

由题设易知，由于()T T T B C A ，，是()s G 的不可简约实现，则存在非奇异阵P ，使得TT T BCPC PB A PAP===--11，，。

由T T T T T T P P I P P P CP P B C C PB =⇒=⇒==⇒=--11 所以P 是非奇异对称阵。

③证明P 的唯一性。

由T C PB =，很容易知道1-=B C P T ，故知P 是唯一的。

综上可知，命题得证。

2-18 解：[]1 1 3- 4 2301 4 0 2- 3-0 3 2- 6-0 02 0 0 0 0 1 -=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=C B A 。

a.① ><B A |由[]⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡==65 17 5 2 3 3 3 3 00 0 0 1 1 1 1 32B A B A AB B U 所以)53012301(|⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡>=<，span B A 。

② η()⇔⋂=kCAker η064 27 118- 145-16 9 34- 43-4 3 10- 13-1 1 3- 4 032=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-⇔=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡x x CACA CA C故)12101301(⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=，span η ③ ><⋂B A |η即任意>⇔<⋂∈B A x |η2153012301x x x ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=，同时有4312101301x x x ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=故0--1 1 5 22 3 3 31 0 0 00 1 1 14321=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡x x x x ，有)1301(|⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡>=<⋂span B A η ④ ⊥><⋂B A |η 易知，⇔>∈<⊥B A x |[]065 17 5 2 3 3 3 3 0 0 0 0 1 1 1 1 32=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=T TxB A B A AB B x，即 065 3 0 117 3 0 15 3 0 12 3 0 1=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡x 所以)0103-0010(|⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=><⊥，span B A 同③，可知⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=><⋂⊥0000|B A η⑤ ><⋂⊥B A |η)101-1-0123(⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=⊥，span η同③可知⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡>=<⋂⊥0000|B A η⑥ ⊥⊥><⋂B A |η易知)0123(|⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=><⋂⊥⊥span B A η 综上可知，上述空间的维数加起来不等于4，故在上述空间的直和空间中不能取到状态空间的基底。

2008级综合大题[]400102110010112x x u y x⎡⎤⎡⎤⎢⎥⎢⎥=-+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦=1 能否通过状态反馈设计将系统特征值配置到平面任意位置？2 控规范分解求上述方程的不可简约形式？3 求方程的传递函数；4 验证系统是否渐近稳定、BIBO 稳定、李氏稳定；（各种稳定之间的关系和判定方法！）5 可能通过状态反馈将不可简约方程特征值配置到-2，-3？若能，确定K ，若不能，请说明理由；6 能否为系统不可简约方程设计全阶状态观测器，使其特征值为-4，-5； 7画出不可简约方程带有状态观测器的状态反馈系统结构图。

参考解答： 1.判断能控性：能控矩阵21416124,() 2.000M BABA B rank M ⎡⎤⎢⎥⎡⎤==-=⎣⎦⎢⎥⎢⎥⎣⎦系统不完全可控，不能任意配置极点。

2按可控规范型分解取M 的前两列，并加1与其线性无关列构成1140120001P -⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦，求得1203311066001P ⎡⎤⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦进行变换[]1120831112,0,22260001A PAP B PB c cP --⎡⎤⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥=-====⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦所以系统不可简约实现为[]08112022x x u y x ⎧⎡⎤⎡⎤=+⎪⎢⎥⎢⎥⎨⎣⎦⎣⎦⎪=⎩3.12(1)(1)2(1)()()(4)(2)(1)(4)(2)s s s G s c sI A B s s s s s --+-=-==-++-+4.det()(4)(2)(1)sI A s s s -=-++，系统有一极点4，位于复平面的右部，故不是渐近稳定。

12(1)()()(4)(2)s G s c sI A B s s --=-=-+，极点为4，-2，存在位于右半平面的极点，故系统不是BIBO 稳定。

系统发散，不是李氏稳定。

5.可以。

令11228,12Tk k k k A Bk k +⎡⎤⎡⎤=+=⎢⎥⎢⎥⎣⎦⎣⎦则特征方程[]2112()det ()(2)28f s sI A Bk s k s k k =-+=-++--期望特征方程*2()(2)(3)56f s s s s s =++=++比较上两式求得：728Tk -⎡⎤=⎢⎥-⎣⎦6.可以。

《线性系统理论》作业参考答案1-1 证明：由矩阵úúúúúúûùêêêêêêëé----=--121000001000010a a a a A n n nL M O M M M L L L则A 的特征多项式为nn n n n n n n n n n n n n n n n n na a a a a a a a a a a a a a a a a A I +++==+--++--=--++--=+--=--------+-----L L L M O MM ML LL L M O M M M L L L L M O MMM L L L112114322111321121)1()1(00001001)1()1(000010001000010001l l l l l l ll l l l l l l l l ll 若i l 是A 的特征值，则00001000010001)(1112121=úúúúúúûùêêêêêêëé+++=úúúúúúûùêêêêêêëéúúúúúúûùêêêêêêëé+--=-----n n i n i n i i i in n ni i i i i a a a a a a A I L M M L M O M M M L L L l l l l l l l l l u l 这表明[]Tn ii i121-l l l L 是i l 所对应的特征向量。

2、①确定特征多项式：
s s 2 s 1 3 ( s) det( sI A) det s 2 s 1 s 1 s 5s 4 s s 2 s 1 2 0, 1 5, 0 4
②确定常数：
2 CB 3
1 CAB 2CB 4
{ 0 CA B 2CAB 1CB 0
2
③确定能控标准型:
0 x 0 0
{ ④线性变换表达式：
1 0 1
y 0
0 0 1 0 0 1 x Bu 0 0 1 x 0 u 2 4 5 0 1
1 2 x 0 4 3 x
0 4 3 1 0 0 5 2 1 0 1 1
p A B
2
1 0 AB B 2 1 1 2
1 4 1 p 0 0
1 7 1 7 1 7
3、 由状态转移矩阵与矩阵指数函数之间的关系 由 (t ) e At A=(0) 二、 1、判断系统能控性
Qc B AB 1 3 1 A B 2 5 10 r Qc 3 故系统能控。 1 1 5
2
1 13 2 7 4 22
④ 全维状态观测器为：
1 0 14 A LC 186 6 1 1220 0 12
1 0 14 14 0 ˆ ( A LC ) x ˆ Ly Bu 186 6 1 x ˆ x 186 y 0 u 1220 0 12 1220 1
四、

标准答案(一)一、填空题（每空1分，共30分）1、无线电通信中，信号是以电磁波形式发射出去的。

它的调制方式有调幅、调频、调相。

2、针对不同的调制方式有三种解调方式，分别是检波、鉴频、和鉴相。

3、在单调谐放大器中，矩形系数越接近于1、其选择性越好；在单调谐的多级放大器中，级数越多，通频带越窄、（宽或窄），其矩形系数越（大或小）小。

4、调幅波的表达式为：uAM（t）= 20（1 +0.2COS100πt）COS107πt（V）；调幅波的振幅最大值为24V，调幅度Ma为20℅，带宽fBW为100Hz，载波fc为5*106Hz。

5、在无线电技术中，一个信号的表示方法有三种，分别是数学表达式、波形、频谱。

6、调频电路有直接调频、间接调频两种方式。

7、检波有同步、和非同步检波两种形式。

8、反馈式正弦波振荡器按照选频网络的不同，可分为LC、RC、石英晶振等三种。

9、变频器可由混频器、和带通滤波器两部分组成。

10、列出三个常见的频谱搬移电路调幅、检波、变频。

11、用模拟乘法器非线性器件实现调幅最为理想。

二、选择题（每小题2分、共20分）将一个正确选项前的字母填在括号内1、下列哪种信号携带有调制信号的信息（C ）A、载波信号B、本振信号C、已调波信号2、小信号谐振放大器的主要技术指标不包含（B ）A、谐振电压增益B、失真系数C、通频带D、选择性3、丙类谐振功放其谐振回路调谐于（ A ）分量A、基波B、二次谐波C、其它高次谐波D、直流分量4、并联型石英晶振中，石英谐振器相当于（C ）元件A、电容B、电阻C、电感D、短路线5、反馈式正弦波振荡器的起振条件为（ B ）A、|AF|=1，φA+φF= 2nπB、|AF| >1，φA+φF = 2nπC、|AF|>1，φA+φF ≠2nπD、|AF| =1，φA+φF ≠2nπ6、要实现集电极调制特性应使功放工作在（B ）状态A、欠压状态B、过压状态C、临界状态D、任意状态7、自动增益控制可简称为（ B ）A、MGCB、AGCC、AFCD、PLL8、利用非线性器件相乘作用来实现频率变换其有用项为（ B ）A、一次方项B、二次方项C、高次方项D、全部项9、如右图所示的电路是（D ）A、普通调幅电路B、双边带调幅电路C、混频器D、同步检波器10、在大信号包络检波器中，由于检波电容放电时间过长而引起的失真是（B）A、频率失真B、惰性失真C、负峰切割失真D、截止失真三、判断题，对的打“√”,错的打“×”（每空1分，共10分）1、谐振放大器是采用谐振回路作负载的放大器。

第一章测试1.研究线性系统的运动规律即系统的分析分为（）分析和（）分析两种( )。

A:非线性B:定性C:定量D:线性答案:BC2.建立线性系统数学模型时，系统中的变量通常有（）。

A:状态变量，输入量，输出量，扰动量四种B:状态变量，输出量，扰动量三种C:状态变量，输入量，扰动量三种答案:A3.数学模型的建立方法有解析法和实验法。

（）A:错B:对答案:B4.传递函数只能描述线性系统。

（）A:对B:错答案:A5.线性系统理论的发展经历了经典线性控制理论和现代线性系统理论两个阶段。

（）A:错B:对答案:B第二章测试1.环境对系统的作用，用（）来表示，系统对环境的作用，用（）来表示，体现系统行为的用（）表示。

A:输入变量输出变量状态变量B:输入变量状态变量输出变量C:输出变量状态变量输入变量D:输出变量输入变量状态变量答案:A2.由方块图描述导出状态空间描述时，我们选取状态变量选取（）作为状态变量。

A:一阶惯性环节的输入端B:一阶惯性环节的输出端答案:B3.线性时不变系统传递函数矩阵在非奇异线性变换下保持不变。

（）A:错B:对答案:B4.由两个或两个以上子系统联接构成的系统称为组合系统，基本组合方式分为串联、并联和反馈联接三种。

（）A:错B:对答案:B5.对于一个系统，建立状态空间表达式时，只有一种状态变量选择。

（）A:错B:对答案:A第三章测试1.系统的强迫运动是指在初始状态为零的情况下系统在外施输入作用下的运动。

（）A:对B:错答案:A2.线性时不变系统的运动响应与初始时刻的选择无关。

（）A:对B:错答案:A3.零初态响应只与系统的输入作用有关。

（）A:对B:错答案:B4.系统的自由运动方程为。

（）A:错B:对答案:A5.系统的状态转移矩阵就等于矩阵指数函数。

（）A:错B:对答案:A第四章测试1.从物理直观性上来看，能控性反映系统的内部状态是否能由输出反映的问题。

（）A:对答案:B2.能达性是指系统的零初始状态在有限时间区间内，通过一个无约束容许控制达到任意指定状态。

C 2《线性系统理论》试卷及答案1、（20分）如图所示RLC 网络，若e(t)为系统输入变量r(t)，电阻R 2两端的电压为输出量y(t)，选定状态变量为 x 1(t)=v 1(t),x 2(t)=v 2(t),x 3(t)=i(t) 要求列写出系统的状态空间描述。

2、（15分）求出下面的输入输出描述的一个状态空间描述。

y (4)+4y (3)+3y (2)+7y (1)+3y=u (3)+ 2u (1)+ 3u3、（15分）计算下列线性系统的传递函数。

[]210X 13101X y -⎡⎤⎡⎤=+⎢⎥⎢⎥-⎣⎦⎣⎦=4、（10分）分析下列系统的能控性。

0111X X u a b ∙⎡⎤⎡⎤=+⎢⎥⎢⎥-⎣⎦⎣⎦5、（10分）分析下列系统的能观性。

[]1110a X X y Xb ∙⎡⎤==-⎢⎥⎣⎦6、（15分）判断下列系统的原点平衡状态x e 是否大范围渐近稳定。

12221123x x x x x x==--7、（15分）已知系统的状态方程为221012000401X X u ∙--⎡⎤⎡⎤⎢⎥⎢⎥=-+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦试确定一个状态反馈阵K ，使闭环极点配置为λ1*=-2、λ2*=-3、λ3*=-4。

答案：1、（20分）如图所示RLC 网络，若e(t)为系统输入变量r(t)，电阻R 2两端的电压为输出量y(t)，选定状态变量为x 1(t)=v 1(t),x 2(t)=v 2(t),x 3(t)=i(t) 要求列写出系统的状态空间描述。

列出向量表示形式解出解出解出r x x x L R x x x rx LR x x x xx x C R x x x C xC x r x R x L L LL⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+--=-=+=+==++1321113211311132122222112211333113000xy x xL2、（15分）求出下面的输入输出描述的一个状态空间描述。

第一章 数学基础1、加法不变性：R(S)中存在零元0，使得对()()S R s f ∈∀，都有()()s f s f =+0成立。

乘法不变性：R(S)中存在单位元1，使得对()()S R s f ∈∀，都有()()()s f s f s f =⋅=⋅11成立。

2、反证法证明：(1)加法不变性的唯一性假设在域F 中，存在0和0’，0≠0’，..t s αααα=+=+'0,0,对F ∈∀α成立。

以α+0=α为例，取α=0’，则0’+0=0’ 因为0’为零元，所以0’+0=0 所以0’=0，与假设矛盾。

（2）乘法不变性的唯一性假设在域F 中，存在1和1’，'11≠，..t s αααααα=⋅=⋅=⋅=⋅'1'1,11,对F ∈∀α成立。

以ααα=⋅=⋅11为例，取'1=α，则有'1'111'1=⋅=⋅ '1为单位元1'111'1=⋅=⋅∴'11=∴ 与假设矛盾3、试用反例证明你对下列问题的回答域交换环 环 []R s 是是 是 n n R *是是 元素[]R s ∈的对角矩阵是是 是 []p R s 是 是 是[]n np R s *是是其中：()p R s 是元素为常态的实有理分式（当s →∞，()R s 有界）；()n n p R s ⨯是元素属于()p R s 的n n ⨯矩阵证明：⑴[]R s 不是域。

如 ()1f +=s s ，显然()[]s R s f ∉-1。

（2）n nR* 不是交换环。

如⎥⎦⎤⎢⎣⎡=1010α，⎥⎦⎤⎢⎣⎡=0101β，显然22⨯∈R βα、。

但是βααβ≠。

（3）不是域。

如⎥⎦⎤⎢⎣⎡+=0001s α，1-α不存在。

（4）()p R s 不是域。

如∈+=1s 1α()p R s ，1-α=s+1.∞→∞→-1α时，s , 所以1-α∉()p R s 。

给定图P2.1(町和(b)所示两个电路，试列写岀其状态方程和输出方程。

其中, 分別指定：⑹状态变II组廿二陀・输入变量“ = 输出变畳尸=f(b)状态变量组齐= u c2 >输入变量输出变量y =(a) O)图P21解本题属于由物理系统尊立状态令间描述的基本题.意在训练正确和熟练运用电路定律列写出电路的状态方程和输出方程。

W列写P2.1(a)电路的状态方程和输川方程。

首先.考虑到电容C和电感I为给定电路中仅有的两个储能元件，电容端电压弋和流经电感电流/构成此电路的线性无关极人变裁组.从而选取状态变量组召=陀和勺符合定义耍求o基此，利用电路元件关系式利回路基尔霍夫定律.定出电路方程为cS d/再由上述电路方程导出状态变量陀和i的导数项..可得到状态变屋方程规范形式,dx 1 & 1丁二一"V u c —匸t + ~e d/ L c L L表u c x<to c/d/和i = d//dn并将上述方程组表为向量方程，就得到此电路的状态方程:继而，按约定输出y =几可直接得到此电路的输出方程：”[0 1卄(b)列写P2.1(b)电路的状态方程和輸出方程。

类似地，考虔到电容C]和C?为给定电路中仅有的两个储能元件，电容端电压呵和叱构成此电路的线性无关极大妾量组，选取状态变量组刁二呵和帀二叱2符合定义要求丿基此，利用电路元件关系式和回路基尔霍夫定律，定出电路方程为du cC&才4匕+七=€++M Q =€再由上述电路方程导出状态变最叱和叱:的导数项，可得到状态变量方程规范形式:表％二血c/击和击，并将上述方程组表为向最方程，就得到此电路的状态方程:继而，按约定输出y讥，可由电路导出:尸％% +七将其表为向量方程，就得到此电路的输出方程！T 1］卜融2・6求岀下列各输入输出描述的一个状态空树描述：⑴笳)—2?十18$+如1 i(s) ?+6?+11J 4-6(ii) 叫 n龜)(g+3)2(zl)解本题属于由传递函数型输入输出描述导出状态空间描述的基本题。