工程力学复习题(静力学部分)说课讲解

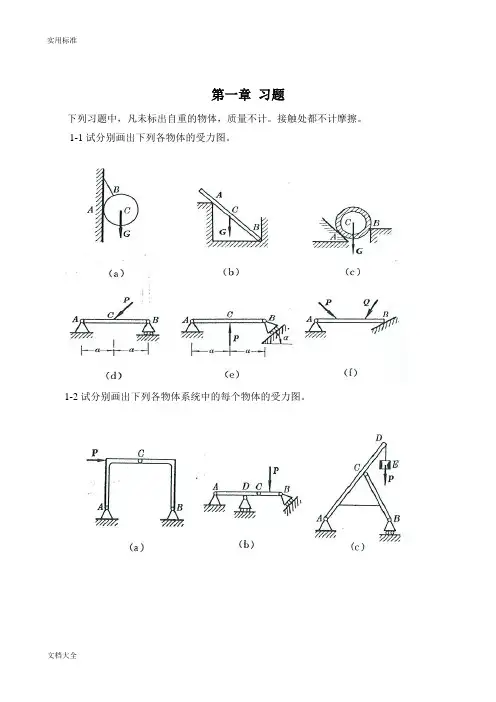
第一章习题下列习题中，凡未标出自重的物体，质量不计。

接触处都不计摩擦。

1-1试分别画出下列各物体的受力图。

1-2试分别画出下列各物体系统中的每个物体的受力图。

1-3试分别画出整个系统以及杆BD，AD，AB（带滑轮C，重物E和一段绳索）的受力图。

1-4构架如图所示，试分别画出杆HED，杆BDC及杆AEC的受力图。

1-5构架如图所示，试分别画出杆BDH，杆AB，销钉A及整个系统的受力图。

1-6构架如图所示，试分别画出杆AEB，销钉A及整个系统的受力图。

1-7构架如图所示，试分别画出杆AEB，销钉C，销钉A及整个系统的受力图。

1-8结构如图所示，力P作用在销钉C上，试分别画出AC，BCE及DEH部分的受力图。

参考答案1-1解：1-2解：1-3解：1-4解：1-5解：1-6解：1-7解：1-8解：第二章 习题参考答案2-1解：由解析法，23cos 80RX F X P P Nθ==+=∑12sin 140RY F Y P P Nθ==+=∑故： 22161.2R RX RY F F F N=+=1(,)arccos2944RYR RF F P F '∠==2-2解：即求此力系的合力，沿OB 建立x 坐标，由解析法，有123cos45cos453RX F X P P P KN==++=∑13sin 45sin 450RY F Y P P ==-=∑故： 223R RX RY F F F KN=+=方向沿OB 。

2-3解：所有杆件均为二力杆件，受力沿直杆轴线。

（a ） 由平衡方程有：0X =∑sin 300ACAB F F -=0Y =∑cos300ACFW -=联立上二式，解得：0.577AB F W =（拉力）1.155AC F W=（压力）（b ） 由平衡方程有：0X =∑cos 700ACAB F F -=0Y =∑sin 700ABFW -=联立上二式，解得：1.064AB F W=（拉力）0.364AC F W=（压力）（c ） 由平衡方程有：0X =∑cos 60cos300ACAB FF -=0Y =∑sin 30sin 600ABAC FF W +-=联立上二式，解得：0.5AB F W=(拉力)0.866AC F W=（压力）（d ） 由平衡方程有：0X =∑sin 30sin 300ABAC F F -=0Y =∑cos30cos300ABAC FF W +-=联立上二式，解得：0.577AB F W =(拉力)0.577AC F W=(拉力)2-4解：（a）受力分析如图所示：由x=∑224cos45042RAF P⋅-=+15.8RAF KN∴=由Y=∑222sin45042RA RBF F P⋅+-=+7.1RBF KN∴=(b)解：受力分析如图所示：由0x =∑3cos 45cos 45010RA RB F F P ⋅--= 0Y =∑1sin 45sin 45010RA RB F F P ⋅+-=联立上二式，得：22.410RA RB F KN F KN==2-5解：几何法：系统受力如图所示三力汇交于点D ，其封闭的力三角形如图示所以： 5RA F KN=（压力）5RB F KN=（与X 轴正向夹150度）2-6解：受力如图所示：已知，1R F G = ，2AC F G =由x =∑cos 0AC r F F α-=12cos G G α∴=由0Y =∑sin 0AC N F F W α+-=22221sin N F W G W G G α∴=-⋅=--2-7解：受力分析如图所示，取左半部分为研究对象由x =∑cos 45cos 450RA CB P F F --=0Y =∑sin 45sin 450CBRA F F '-=联立后，解得：0.707RA F P=0.707RB F P=由二力平衡定理 0.707RB CB CBF F F P '===2-8解：杆AB ，AC 均为二力杆，取A 点平衡由x =∑cos 60cos300AC AB F F W ⋅--=0Y =∑sin 30sin 600ABAC FF W +-=联立上二式，解得：7.32AB F KN =-（受压）27.3AC F KN=（受压）2-9解：各处全为柔索约束，故反力全为拉力，以D ，B 点分别列平衡方程（1）取D 点，列平衡方程由x =∑sin cos 0DB T W αα-=DB T Wctg α∴==（2）取B 点列平衡方程由0Y =∑sin cos 0BD T T αα'-=230BDT T ctg Wctg KN αα'∴===2-10解：取B 为研究对象：由0Y =∑sin 0BC F P α-=sin BC PF α∴=取C 为研究对象：由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑sin cos cos 0BC DC CE F F F ααα--+=联立上二式，且有BCBC F F '= 解得：2cos 12sin cos CE P F ααα⎛⎫=+⎪⎝⎭取E 为研究对象：由0Y =∑cos 0NH CE F F α'-=CECE F F '=故有：22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解：取A 点平衡：0x =∑sin 75sin 750ABAD FF -=0Y =∑cos 75cos 750ABAD FF P +-=联立后可得：2cos 75AD AB PF F ==取D 点平衡，取如图坐标系：0x =∑cos5cos800ADND F F '-=cos5cos80ND ADF F '=⋅由对称性及ADAD F F '=cos5cos5222166.2cos80cos802cos 75N ND AD PF F F KN'∴===⋅=2-12解：整体受力交于O 点，列O 点平衡由x=∑cos cos300RA DCF F Pα+-=Y=∑sin sin300RAF Pα-=联立上二式得：2.92RAF KN=1.33DCF KN=（压力）列C点平衡x=∑405DC ACF F-⋅=Y=∑305BC ACF F+⋅=联立上二式得： 1.67ACF KN=（拉力）1.0BCF KN=-（压力）2-13解：（1）取DEH 部分，对H 点列平衡0x =∑205RD REF F '⋅-= 0Y =∑105RD F Q ⋅-=联立方程后解得： 5RD F Q =2REF Q '=（2）取ABCE 部分，对C 点列平衡0x =∑cos 450RERA FF -= 0Y =∑sin 450RBRA FF P --=且RE REF F '=联立上面各式得： 22RA F Q =2RB F Q P=+（3）取BCE 部分。

工程力学（静力学部分）资料工程力学作业（静力学）班级学号姓名静力学公理和物体的受力分析一、是非题1、在理论力学中只研究力的外效应。

（）2、在平面任意力系中，若其力多边形自行闭合，则力系平衡。

（）3、约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。

（）4、共面三力若平衡，则该三力必汇交于一点。

（）5、当刚体受三个不平行的力作用时，只要这三个力的作用线汇交于同一点，则该刚体一定处于平衡状态。

（）二、选择题1、在下述原理，法则、定理中，只适用于刚体的有_______________。

①二力平衡原理；②力的平行四边形法则；③加减平衡力系原理；④力的可传性原理；⑤作用与反作用定理。

2、三力平衡汇交定理所给的条件是_______________。

①汇交力系平衡的充要条件；②平面汇交力系平衡的充要条件；③不平行的三个力平衡的必要条件。

3、人拉车前进时，人拉车的力_______车拉人的力。

①大于；②等于；③远大于。

三、填空题1、作用在刚体上的两个力等效的条件是：___________________________。

2、二力平衡和作用反作用定律中的两个力，都是等值、反向、共线的，所不同的是：____________________________________________ ______。

3、书P24，1-8题4、画出下列各图中A、B两处反力的方向（包括方位和指向）。

5、在平面约束中，由约束本身的性质就可以确定约束力方位的约束有____________________________________ ____，方向不能确定的约束有______________________________________ ___ (各写出两种约束)。

平面汇交力系与平面力偶系一、是非题1、只要两个力大小相等、方向相反，该两力就组成一力偶。

（）2、用解析法求平面汇交力系的合力时，若选用不同的直角坐标系，则所求得的合力不同。

工程力学复习题跟答案1. 静力学基础- 题目：解释什么是静力平衡，并给出一个简单的例子。

- 答案：静力平衡是指物体在受到多个外力作用下，其合力为零，物体保持静止或匀速直线运动的状态。

例如，悬挂的物体在重力和绳索的拉力作用下保持静止，这两种力相互平衡。

2. 材料力学- 题目：简述材料的弹性模量和屈服强度的概念。

- 答案：弹性模量是材料在弹性范围内应力与应变比值的物理量，它反映了材料的刚性。

屈服强度是指材料在受到外力作用时，从弹性变形过渡到塑性变形的临界应力值。

3. 结构力学- 题目：什么是弯矩，它对结构的影响是什么？- 答案：弯矩是作用在梁或结构上的力矩，它导致结构产生弯曲。

弯矩对结构的影响包括引起结构的变形和应力分布，过大的弯矩可能导致结构的破坏。

4. 动力学- 题目：描述牛顿第二定律，并给出一个应用实例。

- 答案：牛顿第二定律指出，物体的加速度与作用在其上的合力成正比，与物体的质量成反比。

公式为 F = ma。

例如，汽车在加速时，发动机产生的力（F）与汽车的质量（m）和加速度（a）有关。

5. 流体力学- 题目：解释伯努利定律，并说明它在工程中的应用。

- 答案：伯努利定律表明，在理想流体中，流速增加时，流体的静压会减小。

这个原理在飞机的机翼设计中得到应用，通过改变机翼上下方的空气流速，产生升力。

6. 振动分析- 题目：什么是自由振动和阻尼振动，它们有何不同？- 答案：自由振动是指没有外力作用下，系统在初始位移和初始速度下产生的振动。

阻尼振动是指在振动过程中，由于外部阻力（如空气阻力、摩擦力等）的存在，振动幅度逐渐减小的振动。

7. 疲劳分析- 题目：简述什么是疲劳失效，并解释疲劳寿命的基本概念。

- 答案：疲劳失效是指材料在反复加载和卸载过程中，经过一定次数后突然断裂的现象。

疲劳寿命是指材料在反复加载下能够承受的最大循环次数。

8. 非线性力学- 题目：解释什么是非线性力学，并给出一个实际的例子。

- 答案：非线性力学是指那些不遵循线性关系（即应力与应变成正比）的力学现象。

❑第一章静力学基础教学要求：1、熟悉工程力学的研究对象、内容，2、掌握刚体、平衡、力的概念3、掌握五个公理第1、2学时绪论第一篇静力学第1章静力学的基本概念1.1 力的概念1.2 静力学公理1.3 力对点之矩❑刚体▪在力的作用下，其物体内部任意两点之间的距离始终保持不变▪刚体是静力学中对物体进行分析所简化的力学模型❑力▪力是物体间的相互机械作用▪力对物体作用效应➢外效应：使物体的运动状态发生改变；➢内效应：使物体的形状发生改变▪力是矢量▪力的三要素：力的大小、方向、作用线▪力的单位：牛[顿]（N）或千牛（kN）▪分布力和集中力力系❑合力：▪若一个力和一个力系等效，则这个力就称为该力系的合力；力系中的每个力就称为力系的分力；▪将一个复杂力系简化为一个简单力系或一个力的过程，称为力系的简化。

❑力系的分类：▪平面力系：力的作用线均在同一个平面内❑汇交力系：力的作用线汇交于一点；❑平行力系：力的作用线相互平行；❑一般力系：力的作用线既不完全汇交，又不完全平行；▪空间力系❑汇交力系❑平行力系❑一般力系平衡❑定义：▪物体相对于惯性参考系处于静止或匀速直线运动状态。

▪建立在地球上，并相对于地球不动的参考系称为惯性参考系。

❑平衡力系：▪一个物体受某力系作用而处于平衡，则此力系称为平衡力系。

▪力系成为平衡力系而需要满足的条件称为平衡条件。

静力学公理一，❑公理一：力的平行四边形公理▪作用在物体上同一点的两个力可以合成为一个力，合力的作用点仍作用在这一点，合力的大小和方向由这两个力为邻边所构成的平行四边形的对角线确定。

▪矢量表示法：FR=F1+F2❑静力学公理二、三❑公理二：二力平衡公理▪作用于刚体上的两个力使刚体平衡的必要和充分条件是：这两个力的大小相等、方向相反、作用线重合。

▪矢量表示法：F1=－F2；❑公理三：加减平衡力系公理▪在一个刚体上加上或减去一个平衡力系，不改变刚体的原状态。

▪力的可传性原理❑作用于刚体的力可以沿其作用线滑移至刚体的任意点，不改变原力对该刚体的作用效应▪力的三要素：❑力的大小、方向、作用线▪三力平衡条件❑公理四：作用于反作用公理▪任何两个物体相互的作用力和反作用力总是大小相等，方向相反，沿着同一条直线，分别作用在这两个物体上。

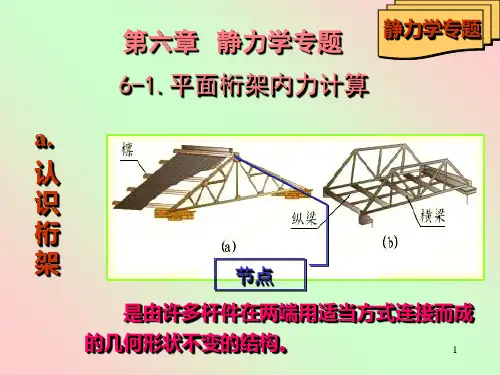
静力学高考研究一、正交分解在平衡分析中的应用【例1】如图所示，质量为m的光滑楔形物块，在水平推力F作用下，静止在倾角为θ的固定斜面上。

则楔形物块受到的斜面支持力大小为( )A．Fsinθ B．mgcosθ C．F/tanθ D．mg/cosθ【例2】如图所示，轻绳MO和NO共同吊起质量为m的重物。

MO与NO垂直，MO与竖直方向的夹角θ ＝30°。

已知重力加速度为g。

则( )【例3】两个相同的小球A和B，质量均为m，用长度相同的两根细线把A、B两球悬挂在水平天花板上的同一点O，并用长度相同的细线连接A、B两小球。

然后用一水平方向的力F作用在小球A上，此时三根线均处于直线状态，且OB线恰好处于竖直方向，如图所示。

如果不考虑两球的大小，两小球均处于静止状态，则力F的大小为( )【例4】如图所示，置于水平地面的三脚架上固定着一质量为m的照相机，三脚架的三根轻质支架等长，与竖直方向均成30°角，则每根支架中承受的压力大小为( )如图所示，一物块置于水平地面上。

当用与水平方向成60°角的力F1拉物块时，物块做匀速直线运动；当改用与水平方向成30°角的力F2推物块时，物块仍做匀速直线运动。

若F1和F2的大小相等，则物块与地面之间的动摩擦因数为( )【例6】L型木板P(上表面光滑)放在固定斜面上，轻质弹簧一端固定在木板上，另一端与置于木板上表面的滑块Q 相连，如图所示。

若P、Q一起沿斜面匀速下滑，不计空气阻力。

则木板P 的受力个数为( )A．3 B．4 C．5 D．6【例7】一质量为m的物块恰好静止在倾角为θ的斜面上。

现对物块施加一个竖直向下的恒力F，如图所示。

则物块( )A．仍处于静止状态B．沿斜面加速下滑C．受到的摩擦力不变D．受到的合外力增大二、关于弹簧问题【例8】如图所示，四个完全相同的弹簧都处于水平位置，它们的右端受到大小皆为F的拉力作用，而左端的情况各不相同：①中弹簧的左端固定在墙上，②中弹簧的右端受大小也为F的拉力作用，③中弹簧的左端拴一小物块，物块在光滑的桌面上滑动，④中弹簧的左端拴一小物块，物块在有摩擦的桌面上滑动。

第一章静力学根底P20-P23 习题：1-1、：F1=2000N，F2=150N， F3=200N， F4=100N，各力的方向如图1-1所示。

试求各力在x、y轴上的投影。

解题提示:计算方法：F x= + F cosαF= + F sinαy注意：力的投影为代数量；式中：F x、F y的“+〞的选取由力F的指向来确定；α为力F与x轴所夹的锐角。

图1-11-2、铆接薄钢板在孔A、B、C、D处受四个力作用，孔间尺寸如图1-2所示。

：F=50N，F2=100N， F3=150N， F4=220N，求此汇交力系的合力。

1解题提示:——计算方法。

一、解析法F=F1x+F2x+……+F n x=∑F xR xF=F1y+F2y+……+F ny=∑F yR yF= √ F R x2+ F R y2Rtanα=∣F R y/ F R x∣二、几何法按力多边形法那么作力多边形，从图1-2图中量得F R的大小和方向。

1-4、求图1-4所示各种情况下力F对点O的力矩。

图1-4解题提示:——计算方法。

①按力矩的定义计算M O〔F〕= + Fd②按合力矩定理计算M O〔F〕= M O〔F x〕+M O〔F y〕1-5、求图1-5所示两种情况下G与F对转心A之矩。

解题提示：此题按合力矩定理计算各力矩较方便、简捷。

以图1-5a为例：力F、G至A点的距离不易确定，如按力矩的定义计算力矩图1-5既繁琐，又容易出错。

假设将力F、G分别沿矩形两边长方向分解，那么各分力的力臂不需计算、一目了然，只需计算各分力的大小，即可按合力矩定理计算出各力的力矩。

M〔F〕= -F cosαb- F sinαaAM〔G〕= -G cosαa/2 - G sinαb/2A1-6、如图1-6所示，矩形钢板的边长为a=4m，b=2m，作用力偶M〔F，F′〕。

当F=F′=200N时，才能使钢板转动。

试考虑选择加力的位置与方向才能使所费力为最小而到达使钢板转一角度的目的，并求出此最小力的值。

工程力学（1）习题全解第4章 刚体静力学专题4－1 塔式桁架如图所示，已知载荷F P 和尺寸d 、l 。

试求杆1、2、3的受力。

解：截面法，受力如图（a ） dl=αtan ，22cos dl d +=α0=∑x F ，0cos 2P =−αF FP 222F dd l F +=（拉） 0=∑AM ，02P 1=⋅−l F d FP 12F dlF =（拉）0=∑y F ，0sin 231=++αF F FP 33F dlF −=（压）4－2 图示构件AE 和EQ 铰接在一起做成一个广告牌。

它承受给定的分布风载。

试求解：（1）先将分布载荷合成于E 点88894.2)7.7402963(8.47.740=×−+×=F N由节点C ，显然 F CQ = 0 （1） （2）截面法，图（a ）0=∑D M ，08.4538.4=××+×−QG F F ，F QG = 14815 N （拉） （2）0=∑B M ，F QD = 00=∑y F ，054=+×BC QG F F ，11852−=BC F N （压） （3） （3）截面法，图（b ）习题4-3图习题4-4图0=∑E M ，08.04.2)7.7402963(212.14.27.7404.253=××−−××−××−AB F2963−=AB F N （压） （4） （4）节点B ，图（c ）0=∑y F ，05454=−−′BQ BC AB F F F ，05411852296354=−+×−BQ F F BQ = 11852 N （拉）（5）0=∑x F ，0)(53=++′BE BQ ABF F F ，0)118522963(53=++−BE F ，5333−=BE F N （压） （6） 又 11852−==BC CD F F N （压）（7）4－3 桁架的载荷和尺寸如图所示。

1 静力学内容讲解1静力学内容讲解1[静力学]内容讲解第一章静力学【竞赛知识要点】重心共点力作用下物体的平衡物体平衡的种类力矩刚体的平衡流体静力学（静止流体中的压强）【内容讲解】一.物体的战略重点1.常见物体的重心：质量均匀分布的三角板的重心在其三条中线的交点；质量均匀分布的半径r的半球体的重心在其对称轴上距球心3r/8处；质量均匀分布的高为h的圆锥体的重心在其对称轴上距顶点为3h/4处。

2.战略重点：在xyz三维坐标系中，将质量为m的物体分割为质点m1、m2、m3……mn.设重心坐标为（x0,y0，z0）,各质点座标为（x1,y1,z1）,(x2,y2,z2)……(xn,yn,zn).那么：mx0=∑miximy0=∑miyimz0=∑mizi【例题】1、（1）存有一质量均匀分布、厚度光滑的直角三角板abc，∠a=30°∠b=90°，该三角板水平置放，被a、b、c三点下方的三个支点提振着，三角板恒定时，a、b、c三点受到的支持力各就是na、nb、nc，则三力的大小关系就是.（2）半径为r的均匀球体，球心为o点，今在此球内挖去一半径为0.5r的小球，且小球恰与大球面内切，则挖去小球后的剩余部分的重心距o点距离为.2、如图所示，质量原产光滑、厚度光滑的梯形板abcd，cd=2ab，求该梯形的战略重点边线。

3、在质量分布均匀、厚度均匀的等腰直角三角形abc（角c为直角）上，切去一等腰三角形apb，如图所示。

如果剩余部分的重心恰在p点，试证明：△apb的腰长与底边长的比为4、（1）质量分别为m,2m,3m……nm的一系列小球（可以视作质点），用长均为l的细绳相连，用短也就是l的细绳立于天花板上，如图所示。

谋总战略重点的边线5、如图所示，质量均匀分布的三根细杆围成三角形abc，试用作图法作出其重心的位置。

6、如图所示，半径为r圆心角为θ的一段质量均匀分布的圆弧，谋其战略重点边线。

第一章静力学基本概念与物体的受力分析下列习题中，未画出重力的各物体的自重不计，所有接触面均为光滑接触。

1.1试画出下列各物体（不包括销钉与支座）的受力图。

解：如图1.2画出下列各物体系统中各物体（不包括销钉与支座）以及物体系统整体受力图。

解：如图F B F Ax A---- M\—2>C 談F N F CFAyBF B (a) FAx J' CF B• %(b)x-7丫AFaFC(d)(C)(e) (f)(g)(h)OAF12 ◎F F(i)1.3铰链支架由两根杆AB、CD和滑轮、绳索等组成，如题 1.3图所示。

在定滑轮上吊有重为W的物体H。

试分别画出定滑轮、杆CD、杆AB和整个支架的受力图。

解：如图1.4题1.4图示齿轮传动系统，O i为主动轮，旋转方向如图所示。

试分别画出两齿轮的受力图。

解: Bxo2y1.5结构如题1.5图所示，试画出各个部分的受力图。

解：第二章汇交力系2.1在刚体的A点作用有四个平面汇交力。

其中F i = 2kN , F2=3kN , F3=lkN , F4=2.5kN , 方向如题2.1图所示。

用解析法求该力系的合成结果。

F1 = 1kN , F2=2kN , F3=|.5kN。

求该力系解F RX=' X = F J COS300 F4 COS450 - F2 COS600 - F3 COS450 = 1.29KN F R y 八丫=F1 sin300 -F4cos450 F2 sin600 - F3 cos450 = 2.54KNF R - F RX F Ry =2.85KN(F R,X)二arctan^ =63.0702.2题2.2图所示固定环受三条绳的作用，已知的合成结果。

解：2.2图示可简化为如右图所示F R^ \ X -F2 F3COS60° =2.75KNF Ry 二'丫二F i —F s Sin600= —0.3KNF R— F RX F Ry =2.77KNF3FRy 0W(F R ,X)二 arctan6.2F Rx2.3力系如题2.3图所示。