电阻混联电路讲解

电阻的混联电路概述电阻混联电路是电路中常见的一种连接方式。

在混联电路中，多个电阻通过并联的方式连接在一起，共享相同的电压源。

本文将对电阻的混联电路进行全面、详细、完整和深入的探讨。

什么是混联电路混联电路是指多个电阻以并联的形式连接在一起，共享相同的电压源。

在混联电路中，电流分流到不同的电阻路径中，然后再汇集到一起。

混联电路的特点是电阻值较小，总电流较大。

混联电路的特性1.并联电阻的总电阻值可以通过公式计算：1 R总=1R1+1R2+1R3+⋯+1R n其中，R总表示并联电阻的总电阻值，R1,R2,R3,…,R n表示每个并联电阻的电阻值。

2.并联电阻的总电流等于各个电阻上的电流之和：I总=I1+I2+I3+⋯+I n其中，I总表示并联电阻的总电流，I1,I2,I3,…,I n表示各个电阻上的电流。

3.并联电阻的总功率等于各个电阻的功率之和：P总=P1+P2+P3+⋯+P n其中，P总表示并联电阻的总功率，P1,P2,P3,…,P n表示各个电阻的功率。

为什么使用混联电路混联电路具有以下几个优点： 1. 降低总电阻：并联电阻的总电阻值小于其中任何一个电阻的电阻值，因此可以有效降低电路的总电阻。

这对于需要大电流通过的电路尤为重要。

2. 分流电流：并联电阻的电流可以分流到不同的路径中，对电路中的各个部分提供所需的电流。

这样可以确保各个电阻和其他电子元件能够正常工作。

3. 共享电压：并联电阻之间共享相同的电压源，这意味着它们可以同时使用相同的电压进行工作，简化了电路设计和布线。

混联电路的应用混联电路广泛应用于各种电子设备和电路中，以下是一些常见的应用场景： 1. 电子元件：在电子元件中，常常需要对不同的部分提供不同的电流，通过混联电路可以实现电流的分流，确保各个部分正常工作。

2. 家庭电路：在家庭电路中，混联电路可以用于将多个电器设备连接到同一个电源插座上，共享电压源，方便使用和管理。

3. 汽车电路：在汽车电路中，混联电路被广泛应用于车载设备和照明系统，可以使多个设备同时使用相同的电源，提供所需的电流。

《电路基础》阻抗的串联、并联和混联实验一. 实验目的1. 通过对电阻器、电感线圈、电容器串联、并联和混联后阻抗值的测量，研究阻抗串、并、混联的特点。

2. 通过测量阻抗，加深对复阻抗、阻抗角、相位差等概念的理解。

3. 学习用电压表、电流表结合画向量图法测量复阻抗。

二. 原理说明1. 交流电路中两个元件串联后总阻抗等于两个复阻抗之和，即：Z总=Z1+Z2两个元件并联，总导纳等于两个元件的复导纳之和，即：Y总=Y1+Y2两个元件并联，然后再与另一个元件串联，则总阻抗应为：Z总=Z3+2121ZZZZ2. 在实验十六中，用V、A、φ表法或V、A、W表法测元件阻抗是很方便的，但如果没有相位表和功率表，仅有电压表和电流表而又欲测复阻抗，则可以用下面所述的画向量图法来确定相位角。

如果图16-1的电阻器和电感线圈的复阻抗有待测量，可以用电压表分别测出有效值U、UR 、UrL，用电流表测出电流有效值I，（电阻R的感性分量可忽略不计，阻性分量计算根据实验十六实际值代入。

）图16-1绘制向量图如图16-2所示。

在绘制向量图时，由于相位角不能测出，只好利用电压U、UR、U rL 组成闭合三角形，根据所测电压值按某比U rLU L U例尺（如每厘米表示3V）截取线段，用几何φφrL方法画出电压三角形，然后根据电阻器的电压R r 与电流同相位，确定画电流向量的位置，电流的图16-2 比例尺也可以任意确定（如每厘米0.1A）。

根据电压表、电流表所测得的值以及从画出的向量图用量角器量出的相位角值，显然可得出复阻抗ZAB 、ZBC及串联后的总阻抗ZAC，从而得出R、L的值。

这种方法也适用于阻抗并联，可以根据上述相似的办法画出电流三角形，再根据其中一支路元件的电压与电流相位关系确定电压向量。

为了使从图中量出的角度精确，建议作图应大一些，即选取电流比例尺小一些，如每厘米代表0.1A 或0.05A。

三. 仪器设备名称数量型号1. 调压器 1台 0-24V2. 相位表/电量仪 1台3. 交流电压、电流表/电量仪 1套4. 万用表 1个5. 电阻器 1个 15Ω*16．电感线圈 1个 28mH*17．电容器 1个 220μF*1四. 任务与步骤1. 研究阻抗的串联、并联和混联（说明：以下所说的电阻器、电感线圈和电容器是指在实验十六中测试过的元件根据实验十六的表1可计算出它们的复阻抗Z1、Z2、Z3或复导纳Y。

电阻混联在电路中的作用全文共四篇示例，供读者参考第一篇示例：电阻的混联是电路中常见的一种连接方式，通过将电阻器并联连接在一起，可以达到一些特定的电路设计要求。

电阻混联的作用是在电路中改变电阻值、调节电流分布等，具有重要的作用。

下面将就电阻混联在电路中的作用进行详细的介绍。

在电阻混联中，电压相同混联是指将多个电阻器并联连接在一起，这些电阻器共享相同的电压源。

这种混联方式可以改变电路的总电阻值，使电路的阻值更贴近设计要求。

在电路设计中，有时会需要增加或减小电阻值，此时可以通过电压相同混联的方式来实现。

电压相同混联还可以调节电路中各个支路的电压分配，使电流分布更加均匀，保证电路正常运行。

除了改变电路的总电阻和调节电流分布外，电阻混联还可以实现功率的分配。

在某些功率较大的电路中，为了保护电阻器不过热，可以采用电压或电流相同混联的方式，将功率均匀分布到各个电阻器中，避免出现局部过载的情况。

第二篇示例：电路中电阻混联是一种常见的电路连接方式，它可以有效地调节电路中的电阻值，起到控制电流、电压和功率的作用。

在实际的电路设计和应用中，电阻混联是非常常见的设计技巧，在各种电子设备和电路中都得到了广泛的应用。

电阻混联是指将多个电阻器以一定的方式连接在一起，形成一个整体电路。

通过调节每个电阻器的阻值，可以实现所需的电路输入输出特性。

电阻混联有两种基本形式：并联和串联。

在并联电路中，电阻器的两端都与电路的两端相连接，而在串联电路中，多个电阻器依次连接在一起，形成一个电阻链条。

电阻混联在电路中起着重要的作用，它可以实现以下几个方面的功能：1. 调节电路的阻值：通过混联多个电阻器，可以实现电阻阻值的调节。

这对于需要调节电路中电流大小或功率的应用非常有用。

通过改变电路中的电阻混联方式，可以实现对电路的性能进行调节。

2. 均压分压：在电路中，混联电阻还可以用于进行均压分压。

通过混联电阻器，可以实现不同电压信号的衰减和分压，使电路可以适应不同的输入和输出信号。

一、实训目的本次实训旨在通过实际操作，加深对电阻混联电路的理解，掌握混联电路的等效电阻计算方法，并学会使用伏安法测量电阻。

通过实训，我们能够提高电路分析能力，增强实际操作技能。

二、实训原理1. 电阻混联电路：在电路中，既有电阻串联又有电阻并联的情况称为电阻的混联。

混联电路的等效电阻可以通过串并联电阻的计算公式进行求解。

2. 等效电阻：等效电阻是指将电路中的多个电阻替换为一个电阻，使电路在功能上等效的电阻值。

对于简单的混联电路，可以使用以下公式计算等效电阻：- 对于串联电路，等效电阻 \( R_{\text{eq}} = R_1 + R_2 + \ldots + R_n \)- 对于并联电路，等效电阻 \( \frac{1}{R_{\text{eq}}} = \frac{1}{R_1} + \frac{1}{R_2} + \ldots + \frac{1}{R_n} \)- 对于串并联混合电路，需要先分别计算串联和并联部分的等效电阻，再进行组合。

3. 伏安法测电阻：伏安法是一种通过测量电阻两端的电压和流过电阻的电流来计算电阻值的方法。

根据欧姆定律 \( R = \frac{U}{I} \)，通过测量电压 \( U \) 和电流 \( I \)，可以计算出电阻值 \( R \)。

三、实训过程1. 实验准备：首先，我们根据实验要求搭建了电阻混联电路，并准备了直流电源、电压表、电流表、电阻等实验器材。

2. 电路搭建：按照电路图连接好电路，确保连接正确无误。

3. 测量电压和电流：打开直流电源，调节电压至适当值，使用电压表测量电阻两端的电压 \( U \)，同时使用电流表测量流过电阻的电流 \( I \)。

4. 计算等效电阻：根据测得的电压和电流值，使用欧姆定律 \( R = \frac{U}{I} \) 计算出电阻值。

5. 多次测量：为了提高实验结果的准确性，我们对电路进行了多次测量，并记录了数据。

6. 数据处理：对实验数据进行处理，求出等效电阻的平均值。

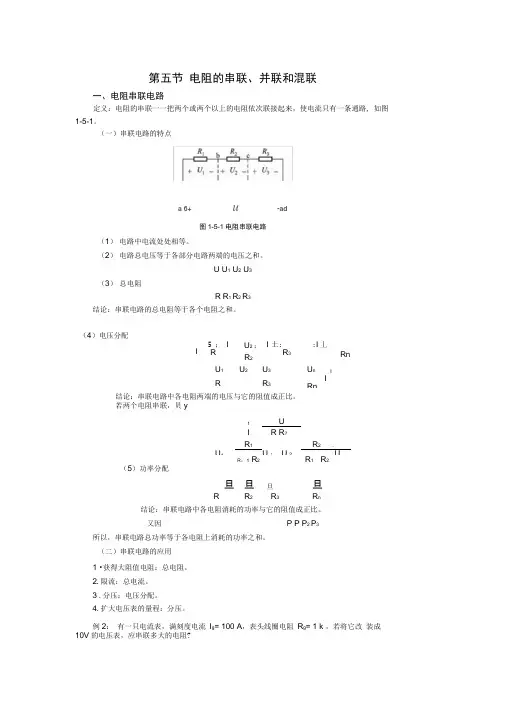
第五节电阻的串联、并联和混联一、电阻串联电路定义：电阻的串联一一把两个或两个以上的电阻依次联接起来，使电流只有一条通路, 如图1-5-1。

（一）串联电路的特点a 6+ u-ad图1-5-1电阻串联电路（1）电路中电流处处相等。

（2）电路总电压等于各部分电路两端的电压之和。

U U1 U2 U3（3）总电阻R R1 R2 R3结论：串联电路的总电阻等于各个电阻之和。

（4）电压分配I 5 ；IRU2 ；R2I 土;R3;I丄Rn U1U2U3U n IR R3I Rn结论：串联电路中各电阻两端的电压与它的阻值成正比。

若两个电阻串联，贝y1UI R R?R1R2 ..U1U ；U 2UR，1 R2R1 R2（5）功率分配旦旦旦旦R R2R3R n结论：串联电路中各电阻消耗的功率与它的阻值成正比。

又因P P P2 P3所以，串联电路总功率等于各电阻上消耗的功率之和。

（二）串联电路的应用1 •获得大阻值电阻：总电阻。

2.限流：总电流。

3 .分压：电压分配。

4.扩大电压表的量程：分压。

例2：有一只电流表，满刻度电流I g= 100 A，表头线圈电阻R g= 1 k ，若将它改装成10V的电压表，应串联多大的电阻?11I、电阻并联电路电阻的并联：把若干个电阻一端连在一起，另一端连接在一起，如图1-5-3。

A A尬r* --- L卜 --------- ---------- [[—-I】 -----------------N A _A0+u—u何（b ）图1-5-3 电阻并联电路（一）并联电路的特点（1）电路中各支路两端的电压相等。

U 1 U 2 U 3（2）电路中总电流等于各支路的电流之和I I 1 I2 13（3）总电阻设电压为U ，根据欧姆定律，则1 = U ； IU ； I U ； I UR 丨1R R 2R n所以1 111 1R瓦瓦R3Rn结论: 并联电路总电阻的倒数，等于各个电阻的倒数之和。

（4）电流分配U =丨1 R 1 = I 2 R 2= I 3 R 3结论：并联电路中通过各个电阻的电流与它的阻值成反比。

混联电路等效电阻的计算混合联接电路是指由串联和并联组成的复杂电路。

在这样的电路中，电流和电压的分布相对复杂，因此需要计算等效电阻来简化电路分析。

计算混合电路的等效电阻需要考虑两种情况：串联情况和并联情况。

下面将分别介绍这两种情况的计算方法。

1.串联情况：在串联电路中，电流只能沿着一条路径流动，因此等效电阻等于电路中各个电阻之和。

例如，如果电路中有3个串联电阻R1、R2和R3，那么等效电阻R等于R1+R2+R3一般来说，如果电路中有n个串联电阻，则等效电阻R等于电路中所有电阻的和，即R=R1+R2+...+Rn。

2.并联情况：在并联电路中，电流可以拆分为多个分支，每个分支通过一个电阻。

等效电阻是并联电阻的倒数之和的倒数。

例如，如果电路中有3个并联电阻R1、R2和R3，那么等效电阻R等于(1/R1+1/R2+1/R3)^(-1)。

一般来说，如果电路中有n个并联电阻，则等效电阻R等于(1/R1+1/R2+...+1/Rn)^(-1)。

当混合电路中既有串联又有并联电阻时，可以按照以下步骤计算等效电阻：步骤1：将电路中的并联电阻用等效电阻替代，这样就可以将电路简化为一个等效串联电路。

步骤2：计算串联电路的等效电阻。

步骤3：将步骤2中计算得到的等效电阻替代原来的并联电阻，这样就可以得到整个混合电路的等效电阻。

需要注意的是，计算混合电路的等效电阻可能会涉及到一些电路定理和公式，例如欧姆定律、基尔霍夫定律等。

在具体计算时还需要考虑电路的性质，如温度、功率、电流方向等。

总结起来，计算混合电路的等效电阻需要先计算串联部分的等效电阻，再计算并联部分的等效电阻，最后将它们组合在一起得到整个电路的等效电阻。

通过这样的计算，可以简化电路的分析和计算。

混联电路小结混联电路是指由多个电阻器组成的电路，其中电阻器并联连接在一起。

混联电路常用来调整电阻的阻值、分压和分流。

混联电路有很多重要的应用，如电子电路、通信系统和电源系统等。

混联电路的特点是可以根据需要调整电路的电压和电流。

在混联电路中，电阻器的总电阻等于各个电阻器的倒数之和的倒数。

这个公式可以简化为：Rt = 1/(1/R1 + 1/R2 + 1/R3 + …)，其中Rt为总电阻，R1、R2、R3等为各个电阻器的电阻。

混联电路实际上是将电流分成几个分支，而每个分支中的电流又根据电阻的大小进行分流。

混联电路的应用有很多。

在电子电路中，混联电路可以用来调整电路的增益和频率响应。

例如，在放大器电路中，可以通过调整混联的电阻值来改变放大器的增益。

在通信系统中，混联电路可以用来进行线路的匹配和调整信号的幅度。

在电源系统中，混联电路可以用来平衡负载和实现电流分配。

混联电路的设计需要考虑多个因素。

首先，需要确定电路的总电阻，以满足需要的电压和电流。

其次，需要选择合适的电阻值，以满足电路的要求。

还需要考虑电阻器的功率耗散，以避免因功率过大而损坏电阻器。

对于混联电路的分析，可以使用基尔霍夫定律和欧姆定律等基本电路定律。

基尔霍夫定律可以应用于电流的分配和电压的分压。

欧姆定律可以应用于电阻器的电压和电流之间的关系。

总之，混联电路是由多个电阻器组成的电路，具有调整电阻的阻值、分压和分流的特点。

混联电路在电子电路、通信系统和电源系统中有重要的应用。

混联电路的设计需要考虑多个因素，并可以使用基尔霍夫定律和欧姆定律等基本电路定律进行分析。