超静定多跨梁的计算

结构力学静定多跨梁例题一个结构力学静定多跨梁例题如下：假设有一根静定多跨梁，有三个等距的支点，梁长为L，弯矩载荷为M。

梁的截面形状为矩形，宽度为b，高度为h。

梁的材料为钢材，弹性模量为E。

求解该横梁在每个支点的支反力。

解题步骤如下：1. 画出梁的剪力图和弯矩图，在每个支点处标注支反力Ra、Rb和Rc。

2. 针对每个支点，应用力平衡条件，即对于任意截面处的受力情况进行分析。

a) 在支点A处，由于该支点不受水平力的作用，只有垂直支反力Ra。

根据力平衡条件，有：Ra = M/L。

b) 在支点B处，有垂直支反力Rb和水平支反力Hb。

由于该支点不受竖直力的作用，有：Rb = Ra + M/L，Hb = 0。

c) 在支点C处，有垂直支反力Rc和水平支反力Hc。

由于该支点不受竖直力的作用，有：Rc = Rb + M/L，Hc = 0。

3. 再应用弯矩平衡条件，根据剪力图和弯矩图的关系求解支反力。

a) 在悬臂端A处，由于支反力Ra是唯一的垂直力，可以得到弯矩方程：Ma = -M。

b) 在支点B处，可以得到弯矩方程：Ma + Mb = 0，即-M + Rb*(L/2) = 0。

c) 在支点C处，可以得到弯矩方程：Ma + Mb + Mc = 0，即-M + Rb*(L/2) + Rc*L = 0。

4. 将以上三个方程联立求解，即可得到支反力Ra、Rb和Rc的具体数值。

需要注意的是，在实际求解过程中，可能还需要考虑其他因素，如材料的应力和变形等。

此处只给出了一个简化的静定多跨梁的例题。

真实的工程问题可能更为复杂，需要综合考虑不同因素进行分析和计算。

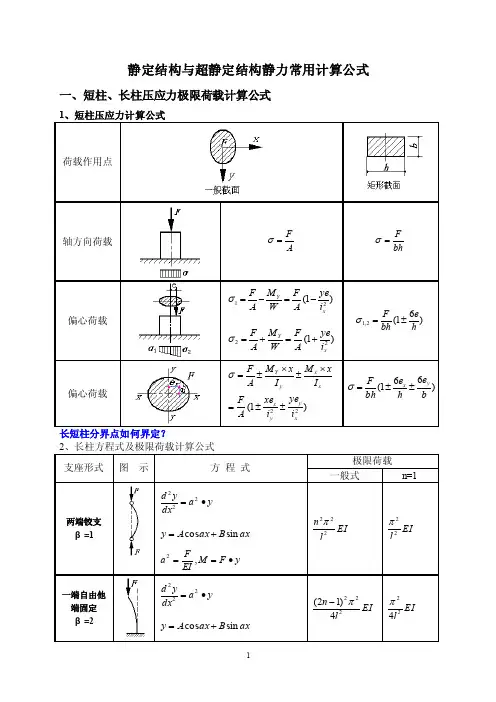
静定结构与超静定结构静力常用计算公式一、短柱、长柱压应力极限荷载计算公式1、短柱压应力计算公式荷载作用点轴方向荷载AF =σ bhF =σ 偏心荷载)1(21xY i ye A F W M A F -=-=σ )1(22xY i ye A F W M A F +=+=σ )61(2,1hebh F ±=σ 偏心荷载)1(22xy y x xx y Y i ye i xe A FI xM I x M A F ±±=⨯±⨯±=σ )661(beh ebh F yx ±±=σ长短柱分界点如何界定？2、长柱方程式及极限荷载计算公式 支座形式图 示方 程 式极限荷载 一般式 n=1两端铰支 β=1y a dxy d ∙=222 ax B ax A y sin cos +=y F M EIFa ∙==,2 EI ln 222π EI l 22π一端自由他端固定β=2y a dxyd ∙=222 ax B ax A y sin cos +=EI l n 2224)12(π-EI l 224πy F M EIFa ∙==,2 两端固定 β=0.50)(22=-+F M y a dxyd A FM ax B ax A y A++=sin cos A M y F M EIFa +∙-==,2 EI l 224π EI l 224π 一端铰支他端固定 β=0.75)(222x l EI Q y a dx y d -=∙+)(sin cos x l FQax B ax A y -++=水平荷载-=Q EIFa ,2 ——EI l227778.1π注：压杆稳定临界承载能力计算公式：EI l P cr 22)(βπ=二、单跨梁的反力、剪力、弯矩、挠度计算公式 1、简支梁的反力、剪力、弯矩、挠度计算公式荷载形式M 图V 图反力 2F R R B A == L Fb R A =L Fa R B =2qL R R B A == 4qL R R B A == 剪力V A =R A V B =-R B V A =R A V B =-R B V A =R A V B =-R BV A =R A V B =-R B弯矩4max FL M =LFabM =max 82maxqL M = 122maxqL M = 挠度EIFL 483max=ω 若a ＞b 时，3)2(932maxab a EIL Fb +=ω（在)2(3b a ax +=处） EIqL 84max=ω EIqL 1204max=ω 注：1、弯矩符号以梁截面下翼缘手拉为正（+），反之为负（—）。

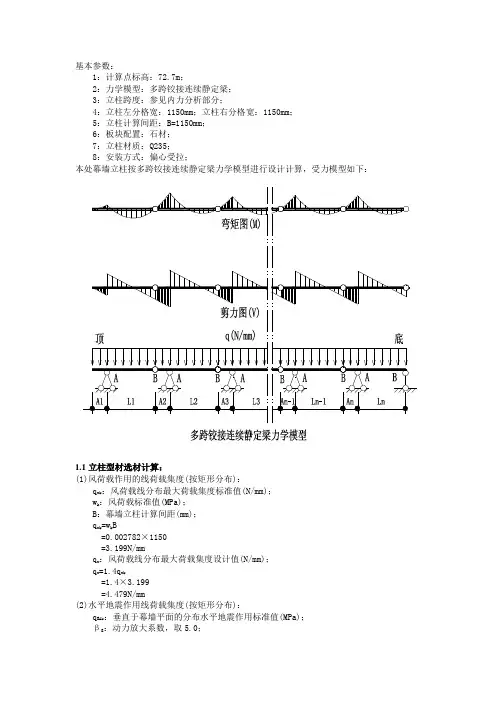
基本参数：1：计算点标高：72.7m；2：力学模型：多跨铰接连续静定梁；3：立柱跨度：参见内力分析部分；4：立柱左分格宽：1150mm；立柱右分格宽：1150mm；5：立柱计算间距：B=1150mm；6：板块配置：石材；7：立柱材质：Q235；8：安装方式：偏心受拉；本处幕墙立柱按多跨铰接连续静定梁力学模型进行设计计算，受力模型如下：1.1立柱型材选材计算：(1)风荷载作用的线荷载集度(按矩形分布)：q wk：风荷载线分布最大荷载集度标准值(N/mm)；w k：风荷载标准值(MPa)；B：幕墙立柱计算间距(mm)；q wk=w k B=0.002782×1150=3.199N/mmq w：风荷载线分布最大荷载集度设计值(N/mm)；q w=1.4q wk=1.4×3.199=4.479N/mm(2)水平地震作用线荷载集度(按矩形分布)：q EAk：垂直于幕墙平面的分布水平地震作用标准值(MPa)；βE：动力放大系数，取5.0；αmax：水平地震影响系数最大值，取0.12；G k：幕墙构件的重力荷载标准值(N)，(含面板和框架)；A：幕墙平面面积(mm2)；q EAk=βEαmax G k/A ……5.3.4[JGJ102-2003]=5×0.12×0.0011=0.00066MPaq Ek：水平地震作用线荷载集度标准值(N/mm)；B：幕墙立柱计算间距(mm)；q Ek=q EAk B=0.00066×1150=0.759N/mmq E：水平地震作用线荷载集度设计值(N/mm)；q E=1.3q Ek=1.3×0.759=0.987N/mm(3)幕墙受荷载集度组合：用于强度计算时，采用S w+0.5S E设计值组合：……5.4.1[JGJ102-2003]q=q w+0.5q E=4.479+0.5×0.987=4.972N/mm用于挠度计算时，采用S w标准值：……5.4.1[JGJ102-2003]q k=q wk=3.199N/mm1.2选用立柱型材的截面特性：按上一项计算结果选用型材号：矩形钢管100×50×4型材的抗弯强度设计值：f s=215MPa型材的抗剪强度设计值：τs=125MPa型材弹性模量：E=206000MPa绕X轴惯性矩：I x=1441300mm4绕Y轴惯性矩：I y=473700mm4绕X轴净截面抵抗矩：W nx1=28830mm3绕X轴净截面抵抗矩：W nx2=28830mm3型材净截面面积：A n=1136mm2型材线密度：γg=0.089176N/mm型材截面垂直于X轴腹板的截面总宽度：t=8mm型材受力面对中性轴的面积矩：S x=18060mm3塑性发展系数：对于钢材龙骨，按JGJ133或JGJ102规范,取1.05；对于铝合金龙骨，按最新《铝合金结构设计规范》GB 50429-2007，取1.00；此处：γ=1.051.3立柱的内力分析：第1跨内力分析：R Bi=qL i×[1-(A i/L i)2]/2-P i×(A i/L i)，i=1=5.026×3060×[1-(800/3060)2]/2-0×(800/3060)=7164NM i=qL i2×[1-(A i/L i)2]2/8，i=1=5.026×30602×[1-(800/3060)2]2/8=5106004N·mm第2跨内力分析：P i=R Bi-1，i=2=7164NR Bi=qL i×[1-(A i/L i)2]/2-P i×(A i/L i)，i=2=5.026×3200×[1-(700/3200)2]/2-7164×(700/3200)=6090NM i=qL i2×[1-(A i/L i)2]2/8-P i×A i×[1-(1+(A i/L i))2/2+A i/L i]，i=2=5.026×32002×[1-(700/3200)2]2/8-7164×700×[1-(1+(700/3200)2/2+700/3200] =3444909N·mmM A2=-(P i×A i+qA i2/2)，(i=2)=-6246170N·mm第3跨内力分析：P i=R Bi-1，i=3=6090NR Bi=qL i×[1-(A i/L i)2]/2-P i×(A i/L i)，i=3=5.026×3200×[1-(700/3200)2]/2-6090×(700/3200)=6325NM i=qL i2×[1-(A i/L i)2]2/8-P i×A i×[1-(1+(A i/L i))2/2+A i/L i]，i=3=5.026×32002×[1-(700/3200)2]2/8-6090×700×[1-(1+(700/3200)2/2+700/3200] =3802821N·mmM A3=-(P i×A i+qA i2/2)，(i=3)=-5494370N·mm第4跨内力分析：P i=R Bi-1，i=4=6325NR Bi=qL i×[1-(A i/L i)2]/2-P i×(A i/L i)，i=4=5.026×3200×[1-(700/3200)2]/2-6325×(700/3200)=6273NM i=qL i2×[1-(A i/L i)2]2/8-P i×A i×[1-(1+(A i/L i))2/2+A i/L i]，i=4=5.026×32002×[1-(700/3200)2]2/8-6325×700×[1-(1+(700/3200)2/2+700/3200] =3724507N·mmM A4=-(P i×A i+qA i2/2)，(i=4)=-5658870N·mm第5跨内力分析：P i=R Bi-1，i=5=6273NR Bi=qL i×[1-(A i/L i)2]/2-P i×(A i/L i)，i=5=5.026×3200×[1-(700/3200)2]/2-6273×(700/3200)=6285NM i=qL i2×[1-(A i/L i)2]2/8-P i×A i×[1-(1+(A i/L i))2/2+A i/L i]，i=5=5.026×32002×[1-(700/3200)2]2/8-6273×700×[1-(1+(700/3200)2/2+700/3200] =3741836N·mmM A5=-(P i×A i+qA i2/2)，(i=5)=-5622470N·mm第6跨内力分析：P i=R Bi-1，i=6=6285NR Bi=qL i×[1-(A i/L i)2]/2-P i×(A i/L i)，i=6=5.026×3200×[1-(700/3200)2]/2-6285×(700/3200)=6282NM i=qL i2×[1-(A i/L i)2]2/8-P i×A i×[1-(1+(A i/L i))2/2+A i/L i]，i=6=5.026×32002×[1-(700/3200)2]2/8-6285×700×[1-(1+(700/3200)2/2+700/3200] =3737837N·mmM A6=-(P i×A i+qA i2/2)，(i=6)=-5630870N·mm第7跨内力分析：P i=R Bi-1，i=7=6282NR Bi=qL i×[1-(A i/L i)2]/2-P i×(A i/L i)，i=7=5.026×3200×[1-(700/3200)2]/2-6282×(700/3200)=6283NM i=qL i2×[1-(A i/L i)2]2/8-P i×A i×[1-(1+(A i/L i))2/2+A i/L i]，i=7=5.026×32002×[1-(700/3200)2]2/8-6282×700×[1-(1+(700/3200)2/2+700/3200] =3738837N·mmM A7=-(P i×A i+qA i2/2)，(i=7)=-5628770N·mm第8跨内力分析：P i=R Bi-1，i=8=6283NR Bi=qL i×[1-(A i/L i)2]/2-P i×(A i/L i)，i=8=5.026×3200×[1-(700/3200)2]/2-6283×(700/3200)=6282NM i=qL i2×[1-(A i/L i)2]2/8-P i×A i×[1-(1+(A i/L i))2/2+A i/L i]，i=8=5.026×32002×[1-(700/3200)2]2/8-6283×700×[1-(1+(700/3200)2/2+700/3200] =3738504N·mmM A8=-(P i×A i+qA i2/2)，(i=8)=-5629470N·mm第9跨内力分析：P i=R Bi-1，i=9=6282NR Bi=qL i×[1-(A i/L i)2]/2-P i×(A i/L i)，i=9=5.026×3200×[1-(700/3200)2]/2-6282×(700/3200)=6283NM i=qL i2×[1-(A i/L i)2]2/8-P i×A i×[1-(1+(A i/L i))2/2+A i/L i]，i=9=5.026×32002×[1-(700/3200)2]2/8-6282×700×[1-(1+(700/3200)2/2+700/3200] =3738837N·mmM A9=-(P i×A i+qA i2/2)，(i=9)=-5628770N·mm第10跨内力分析：P i=R Bi-1，i=10=6283NR Bi=qL i×[1-(A i/L i)2]/2-P i×(A i/L i)，i=10=5.026×3200×[1-(700/3200)2]/2-6283×(700/3200)=6282NM i=qL i2×[1-(A i/L i)2]2/8-P i×A i×[1-(1+(A i/L i))2/2+A i/L i]，i=10=5.026×32002×[1-(700/3200)2]2/8-6283×700×[1-(1+(700/3200)2/2+700/3200] =3738504N·mmM A10=-(P i×A i+qA i2/2)，(i=10)=-5629470N·mm第11跨内力分析：P i=R Bi-1，i=11=6282NR Bi=qL i×[1-(A i/L i)2]/2-P i×(A i/L i)，i=11=5.026×3200×[1-(700/3200)2]/2-6282×(700/3200)=6283NM i=qL i2×[1-(A i/L i)2]2/8-P i×A i×[1-(1+(A i/L i))2/2+A i/L i]，i=11=5.026×32002×[1-(700/3200)2]2/8-6282×700×[1-(1+(700/3200)2/2+700/3200] =3738837N·mmM A11=-(P i×A i+qA i2/2)，(i=11)=-5628770N·mm第12跨内力分析：P i=R Bi-1，i=12=6283NR Bi=qL i×[1-(A i/L i)2]/2-P i×(A i/L i)，i=12=5.026×3200×[1-(700/3200)2]/2-6283×(700/3200)=6282NM i=qL i2×[1-(A i/L i)2]2/8-P i×A i×[1-(1+(A i/L i))2/2+A i/L i]，i=12=5.026×32002×[1-(700/3200)2]2/8-6283×700×[1-(1+(700/3200)2/2+700/3200] =3738504N·mmM A12=-(P i×A i+qA i2/2)，(i=12)=-5629470N·mm第13跨内力分析：P i=R Bi-1，i=13=6282NR Bi=qL i×[1-(A i/L i)2]/2-P i×(A i/L i)，i=13=5.026×3200×[1-(700/3200)2]/2-6282×(700/3200)=6283NM i=qL i2×[1-(A i/L i)2]2/8-P i×A i×[1-(1+(A i/L i))2/2+A i/L i]，i=13=5.026×32002×[1-(700/3200)2]2/8-6282×700×[1-(1+(700/3200)2/2+700/3200] =3738837N·mmM A13=-(P i×A i+qA i2/2)，(i=13)=-5628770N·mm第14跨内力分析：P i=R Bi-1，i=14=6283NR Bi=qL i×[1-(A i/L i)2]/2-P i×(A i/L i)，i=14=5.026×3200×[1-(700/3200)2]/2-6283×(700/3200)=6282NM i=qL i2×[1-(A i/L i)2]2/8-P i×A i×[1-(1+(A i/L i))2/2+A i/L i]，i=14=5.026×32002×[1-(700/3200)2]2/8-6283×700×[1-(1+(700/3200)2/2+700/3200] =3738504N·mmM A14=-(P i×A i+qA i2/2)，(i=14)=-5629470N·mm第15跨内力分析：P i=R Bi-1，i=15=6282NR Bi=qL i×[1-(A i/L i)2]/2-P i×(A i/L i)，i=15=5.026×3200×[1-(700/3200)2]/2-6282×(700/3200)=6283NM i=qL i2×[1-(A i/L i)2]2/8-P i×A i×[1-(1+(A i/L i))2/2+A i/L i]，i=15=5.026×32002×[1-(700/3200)2]2/8-6282×700×[1-(1+(700/3200)2/2+700/3200] =3738837N·mmM A15=-(P i×A i+qA i2/2)，(i=15)=-5628770N·mm第16跨内力分析：P i=R Bi-1，i=16=6283NR Bi=qL i×[1-(A i/L i)2]/2-P i×(A i/L i)，i=16=5.026×3200×[1-(700/3200)2]/2-6283×(700/3200)=6282NM i=qL i2×[1-(A i/L i)2]2/8-P i×A i×[1-(1+(A i/L i))2/2+A i/L i]，i=16=5.026×32002×[1-(700/3200)2]2/8-6283×700×[1-(1+(700/3200)2/2+700/3200] =3738504N·mmM A16=-(P i×A i+qA i2/2)，(i=16)=-5629470N·mm关键词：幕墙立柱计算结构应力优化摘要：本文经过对三种幕墙立柱的受力分析，明确了每种立柱的最佳适用工况。

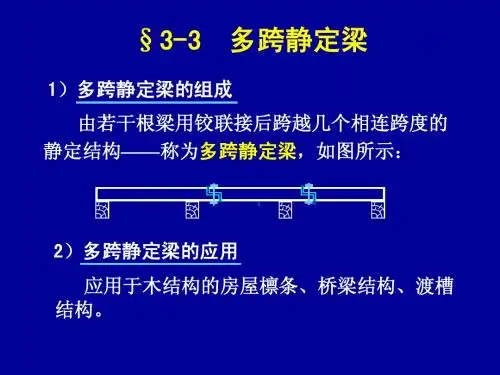
5.2 多跨静定梁的内力计算与内力图绘制一、多跨静定梁的组成单跨静定梁多使用于跨度不大的情况，如门窗、楼板、屋面大梁、短跨的桥梁以及吊车梁等。

通常将若干根单跨梁用铰相连，并用若干支座与基础连接而组成的静定结构称为多跨静定梁。

如图5. 19(a)所示为房屋建筑中一木檩条的结构图，在各短梁的接头处采用斜搭接加螺栓系紧。

由于接头处不能抵抗弯矩，因而视为铰结点。

其计算简图如图5. 19(b)所示。

从几何组成上看，多跨静定梁的组成部分可分为基本部分和附属部分。

如图5. 19(b)所示，其中梁AB 部分，有三根支座链杆直接与基础（屋架）相连，不依赖其它部分构成几何不变体系，称为基本部分；对于梁的EF 和IJ 部分，因它们在竖向荷载作用下，也能独立保持平衡，故在竖向荷载作用下，可以把它们当作基本部分；而短梁CD 和GH 两部分支承在基本部分之上，需依靠基本部分才能保持其几何不变性，故称为附属部分。

为了清楚地看到梁各部分之间的依存关系和力的传递层次，可以把基本部分画在下层，把附属部分画在上层，如图5.19(c)所示，称为层次图。

BCDEFG H I(f)(g)AB CD E F GHA BCDE F GHII(a)(b)(c)(d)(e)ABCDEF GHIA B C D E F G H I JABCD EFG H IJ檩条屋架上弦图5.19二、多跨静定梁的内力计算从受力分析看，由于基本部分能独立地承受荷载而维持平衡，故当荷载作用于基本部分时，由平衡条件可知，将只有基本部分受力，附属部分不受力。

而当荷载作用于附属部分时，则不仅附属部分受力，其反力将通过铰结处传给基本部分，使基本部分同时受力。

由上述基本部分和附属部分力的传递关系可知，多跨静定梁的计算顺序应该是先计算附属部分，后计算基本部分。

计算附属部分时，应先从附属程度最高的部分算起；计算基本部分时，把计算出的附属部分的约束力反其方向，作为荷载作用于基本部分。

§1.3超静定结构的计算超静定结构是具有多余约束的几何不变体系，仅根据静力平衡条件不能求出其全部支座反力和内力，还须考虑变形协调条件。

计算超静定结构的基本方法是力法和位移法。

这两种基本方法的解题思路，都是设法将未知的超静定结构计算问题转换成已知的结构计算问题。

转换的桥梁就是基本体系，转换的条件就是基本方程，转换后要解决的关键问题就是求解基本未知量。

1.3.1力法力法是以多余未知力为基本未知量、一般用静定结构作为基本结构，以变形协调条件建立基本方程来求解超静定结构内力的计算方法。

超静定结构多余约束（或多余未知力）的数目称为超静定次数，用n表示。

确定超静定次数的方法是：取消多余约束法，即去掉超静定结构中的多余约束，使原结构变成静定结构，所去掉的多余约束的数目即为原结构的超静定次数。

在结构上去掉多余约束的方法，通常有如下几种：●切断一根链杆，或者移去一个支座链杆，相当于去掉一个约束；●将一个固定支座改成固定铰支座，或将受弯杆件某处改成铰接，相当于去掉一个抗转动约束；●去掉一个联结两刚片的铰，或者撤去一个固定铰支座，相当于去掉两个约束；●将一梁式杆切断，或者撤去一个固定支座，相当于去掉三个约束。

现以图1-26a所示一次超静定结构为例，说明力法的基本原理。

其中，要特别重视力法的三个基本概念。

图1-261、力法的基本未知量：取超静定结构中的多余未知力（如图1-26a 中的X1）作为力法的基本未知量，以X i表示。

多余未知力在超静定结构内力分析中处于关键的地位，因此，有必要将其突出出来，作为主攻目标。

力法这个名称也因此而得。

2、力法的基本体系：将原结构中的多余约束（如图1-26a中的支座B）去掉，所得到的无任何外加因素的结构，称为力法的基本结构（图1-26b）；基本结构在荷载和多余未知力共同作用下的体系，称为力法的基本体系（图1-26c）。

在基本体系中，仍然保留原结构的多余约束反力X1，只是把它由被动力改为主动力，因此基本体系的受力状态与原结构完全相同。

计算多跨静定梁时，可以按照以下步骤进行计算顺序：
1. 确定梁的支座类型和位置：首先确定梁的支座类型，例如固定支座、铰支座或滑动
支座，并确定它们的位置。

2. 划分梁的跨数：根据实际情况，将梁划分为多个跨。

3. 确定每个跨的边界条件：对于每个跨，确定其边界条件，如支座反力、弯矩、剪力等。

4. 单独计算每个跨的内力：对于每个跨，使用适当的方法（如力法、位移法或弯矩法）计算其内力分布。

5. 跨间连续性条件的处理：对于相邻的两个跨，考虑它们之间的连续性条件，例如弯
矩连续性条件。

6. 解算未知反力：根据边界条件和连续性条件，解算出所有跨的未知反力。

7. 检验静定条件：检查所得到的反力是否符合静定条件，即受力平衡和变形平衡。

8. 计算梁的内力分布：根据已知的反力和边界条件，计算梁的内力分布，如弯矩、剪
力和轴力。

9. 校验计算结果：检查计算结果是否满足设计要求，如强度、刚度和稳定性等。

请注意，以上仅为一般情况下多跨静定梁计算的顺序，具体问题具体分析，可能需要
根据实际情况进行调整。

同时，如果你有特定的问题或需要更详细的计算步骤，请提
供更多信息，我将尽力提供帮助。

静定多跨梁支座的弯矩计算【最新版】目录1.引言2.静定多跨梁的支座弯矩计算方法3.计算过程详解4.结论5.参考文献正文1.引言在结构力学中，静定多跨梁是一种常见的结构形式。

在实际工程中，为了确保结构的安全性和稳定性，需要对其进行内力分析，其中支座弯矩是重要的分析指标之一。

本文将对静定多跨梁支座的弯矩计算方法进行详细探讨。

2.静定多跨梁的支座弯矩计算方法静定多跨梁的支座弯矩计算可以采用叠加法。

具体步骤如下：（1）将多跨梁分解为附属部分和基本部分。

附属部分通常包括连续梁和简支梁，而基本部分则是静定梁。

（2）先计算附属部分的支座弯矩，并将其作为基本部分的荷载。

（3）计算基本部分的支座弯矩，即将附属部分的支座弯矩与基本部分的其他荷载（如均布荷载、集中荷载等）进行叠加。

3.计算过程详解以一个三跨静定梁为例，假设梁的材料是均质的，截面是均匀的，且各截面上的荷载是均匀分布的。

（1）计算附属部分的支座弯矩附属部分为连续梁，可以根据连续梁的弯矩公式进行计算。

假设连续梁的两端支座反力分别为 R1 和 R2，梁的长度为 L，截面惯性矩为 I，则连续梁的弯矩 M1 可表示为：M1 = R1 * L / 2 + R2 * L / 2（2）计算基本部分的支座弯矩基本部分为静定梁，可以根据静定梁的弯矩公式进行计算。

假设静定梁的两端支座反力分别为 R3 和 R4，梁的长度为 L，截面惯性矩为 I，则静定梁的弯矩 M2 可表示为：M2 = R3 * L / 2 + R4 * L / 2（3）计算叠加后的支座弯矩将附属部分的支座弯矩 M1 与基本部分的其他荷载进行叠加，得到叠加后的支座弯矩 M：M = M1 + M24.结论通过以上计算过程，可以得到静定多跨梁支座的弯矩。

在实际工程中，该方法可以有效地分析结构的内力分布，为设计和施工提供重要依据。

5.参考文献[1] 张三，李四。

静定多跨梁支座的弯矩计算 [J].钢结构，2020, 30(2): 12-17.[2] 王五，赵六。

多跨连续梁板的内力计算方法1.静力法静力法是根据力的平衡条件进行内力计算的一种方法。

它将整个连续梁板分成多个简支梁，然后根据每个简支梁的自由度和受力情况，利用静力平衡方程来计算内力。

静力法的计算步骤如下：1.1确定荷载情况：根据施工过程中的荷载情况，包括永久荷载、临时荷载、活荷载等，确定在每个简支梁上的作用荷载。

1.2确定支座反力：根据简支梁的支座类型和约束条件，利用静力平衡方程计算得到每个简支梁的支座反力。

1.3确定剪力和弯矩分布：根据简支梁的自由度和受力平衡条件，分别计算每个简支梁的剪力和弯矩分布，并绘制剪力和弯矩图。

1.4超程状态求解：对于超程段，根据断面力和弯矩图的性质，分别计算超程段的剪力和弯矩值。

1.5内力计算：根据每个简支梁上的受力条件和简支梁的自由度，依次计算出每个简支梁的内力值，包括剪力、弯矩和轴力。

1.6跨中内力的计算：将每个简支梁上的内力加权平均，得到整个连续梁板跨中截面所受的内力值。

注意事项：在使用静力法计算连续梁板的内力时，需要注意简支梁之间的相互作用和连梁处的内力传递。

2.变形法变形法是根据结构变形的平衡条件进行内力计算的一种方法。

它将整个连续梁板看作一个整体，利用结构变形平衡方程来计算内力。

变形法的计算步骤如下：2.1建立变形方程：根据连续梁板的几何形状和材料特性，建立连续梁板的位移和变形关系。

2.2确定加载形态：根据施工过程中的荷载情况，确定连续梁板的加载形态，包括简支挠度和弯矩分布。

2.3利用变形方程求解：根据变形方程和加载形态，利用几何和材料力学关系，求解出每个简支梁的弯矩和剪力分布。

2.4变形体内力计算：根据连续梁板的几何和材料力学关系，将每个简支梁上的弯矩和剪力分布转化为变形体上的内力分布。

2.5跨中内力的计算：将变形体上的内力分布加权平均，得到整个连续梁板跨中截面所受的内力值。

注意事项：在使用变形法计算连续梁板的内力时，需要考虑材料的非线性特性和位移场的复杂性，适用于较复杂的结构形式。

超静定多跨梁的计算吴郁斌力法的原理及二次超静定多跨梁的计算思路力法是计算超静定结构的最基本的方法。

采用力法解决超静定结构问题时，不是孤立地研究超静定问题，而是把超静定问题与静定问题联系起来，加以比较，从而把超静定结构问题转化为静定结构问题来加以解决。

在解决超静定多跨梁结构问题时，首先要确定超静定的次数，如下图所示：图一图一所示的静定多跨梁中，经分析得知，结构中的B 、C 两点的约束为多余约束，所以该结构为二次超静定问题。

其次，在确定超静定次数之后，按力学方法对模型进行转化，将超静定结构转变为静定结构。

在图一所示的结构中，我们先假设B 、C 两点无约束，而作用两个集中力C B F F 、，方向按图一所示，这样我们就把一个超静定多跨梁结构转化成简支梁结构，从而把解决超静定多跨梁结构的问题也转化成解决简支梁的问题。

最后，找出结构转化过程中的限制条件，按照条件列出力法方程。

在图一所示的结构中，当我们把超静定多跨梁结构转化成简支梁的过程中，我们必须限制B 、C 两点的竖向位移为0，因为在原来的超静定多跨梁结构中，B 、C 两点有约束。

然后根据限制条件列出力法方程。

假设作用于多跨梁上的载荷在B 、C 两点产生的竖向位移分别为1∆和2∆，作用于B 点的单位竖向力（即当1=B F 时）在B 、C 两点产生的竖向位移分别为1211δδ和，作用于C 点的单位竖向力（即当1=C F 时）在B 、C 两点产生的竖向位移分别为21δ和22δ。

设作用于B 、C 两点的实际作用力大小分别为倍的单位力、21X X 。

我们都知道梁的位移与载荷的大小成正比，所以根据限制条件以及假设条件，可以列出如下方程：⎩⎨⎧=∆-⋅+⋅=∆-⋅+⋅0022221211212111X X X X δδδδ 通过上述方程就可以计算出B 、C 两点的支座反力C B F F 、,然后通过力平衡方程和弯矩平衡方程就可以解出两外两点（A 、D 两点）的支座反力，即⎪⎩⎪⎨⎧==∑∑00y A M F ,⇒()⎩⎨⎧=⋅+⋅-+⋅+⋅=+++0a 0211y L F F L L F L F F F F F D C B D C B A 解之，就可以得到各个支座的反力，进而得到梁上各段的剪力图和弯矩图了。

任务二十四多跨静定梁的内力计算一、填空题1.若干根梁用铰相联，并用若干支座与基础相联而组成的结构称为（多跨静定梁）。

2.多跨静定梁几何组成上可分为（基本部分）和（附属部分）。

3.（基本部分 )是指不依赖其他部分的存在而能独立地维持其几何不变性的部分。

4.（附属部分)是指必须依靠基本部分才能维持其几何不变形的部分。

5.多跨静定梁的内力计算当中，为了表示梁各部分之间的支撑关系，把基本部分画在下层，而把附属部分画在上层，称为（层叠图）。

6.作用在基本部分上的力（不传递给）附属部分，而作用在附属部分上的力（传递给）基本部分。

7.计算多跨静定梁时应该是先（附属部分）后（基本部分）。

8.多跨静定梁在附属部分受竖向荷载作用时，必会引起（基本部分）的内力。

二、画内力图1. 作多跨静定梁的剪力图和弯矩图。

解：先作出多跨静定梁的层次图和层次受力图如图b、c所示。

（1）计算反力如图c所示，由附属部分开始计算，由对称性可得Fdy=Fcy=30KN再计算基本部分AC梁的反力。

由 MA=0，MB=0 可以得到QA=FA=25KNQB=FB=85KN（2）作剪力图和弯矩图各支座反力求出后，分别绘制AC段和CD段的剪力图和弯矩图，即组成了整个多跨静定梁的剪力图和弯矩图，分别如图d、e所示。

2.作图所示多跨静定梁的剪力图和弯矩图解： 图（a ）所示多跨静定梁，由于仅受竖向荷载作用，故AB 和CE 都为基本部分，其层次图如图（b ）所示。

各根梁的隔离体示于图（c ）中。

从附属部分BC 开始，依次求出各根梁上的竖向约束力和支座反力。

铰C 处的水平约束力为零，并由此得知铰B 处的水平约束力也等于零。

求出各约束力和支座反力后，便可分别绘出各根梁的内力图。

将各根梁的内力图置于同一基线上，则得出该多跨静定梁的内力图如图（d ）、（e ）所示。

在FG ，GD 两上区段剪力FQ 是同一常数，由微分关系QF dx dM可知这两区段内的弯矩图形有相同的斜率。

静定多跨梁支座的弯矩计算
静定多跨梁的弯矩计算可以通过以下步骤进行：
1. 首先，确定每个支座的支座反力。

这可以通过平衡力的原理得到，即每个支座的反力等于该支座对应跨度上的受力的代数和。

2. 然后，根据支座反力计算跨梁上的积点力。

积点力是与每个支座反力成正比的长度系数。

3. 接下来，分析每个跨梁上的自由弯矩。

自由弯矩是在没有外力作用下的梁的弯曲情况。

可以通过梁的截面特性和边界条件计算出每个跨梁上的自由弯矩。

4. 最后，考虑外力对每个跨梁的影响，根据受力平衡条件计算出受力跨度上的弯矩分布。

这可以通过将支座反力和积点力施加到跨梁上，并使用梁的受力分析方法进行计算得到。

需要注意的是，静定多跨梁的弯矩计算可能较为复杂，需要考虑梁的几何形状、材料性质、边界条件和外力情况等因素。

因此，在实际应用中，通常使用专业的结构分析软件或进行精确的结构计算来得到准确的弯矩结果。