频率分布直方图的画法

简要说明绘制频率分布直方图的步骤
绘制频率分布直方图是统计学中比较重要的一种数据可视化分析方法，它可以帮助我们进行数据的分析和可视化。

绘制频率分布直方图的步骤是：
首先，收集相应的数据，这需要我们确定要分析的相应的变量，分类或者定量的变量，对定性变量可以从提供的各种状态的列表中进行选择，而对定量变量可以变分组，例如男性和女性，或者按照星级分类等。

其次，确定x轴和y轴，x轴表示变量的值，当变量是定量变量时，x轴为某类因数的值，如果是定性变量，则x轴为定性变量的状态值，而y轴表示实际的频率数据。

第三，当画图时，我们根据以上两个轴的数据以及频率数据，使用计算机绘制频率分布直方图，其中可以自由控制图表的形态，字体，颜色等特征，以更好地反映出数据的趋势及其重要性。

最后，绘制完成后，可以根据图表给出对数据的准确解读。

综上所述，绘制频率分布直方图是一个非常重要的统计学可视化分析方法，熟练掌握这个方法可以帮助我们更好地分析数据。

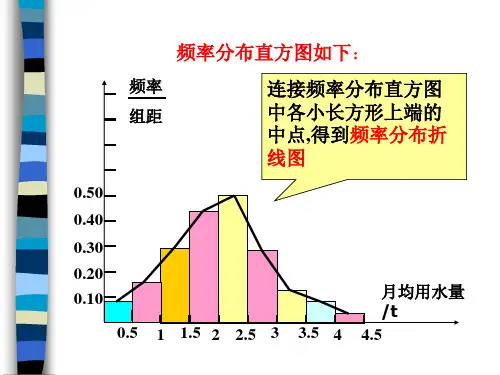
频率分布直方图作频率分布直方图的方法为：（1）把横轴分成若干段，每一线段对应一个组的组距；（2）以此线段为底作矩形，它的高等于该组的组距频率，这样得出一系列的矩形；（3）每个矩形的面积恰好是该组上的频率.频率折线图：如果将频率分布直方图中各相邻的矩形的上底边的中点顺次连接起，就得到一条折线，称这条折线为本组数据的频率折线图.作茎叶图的方法是：将所有两位数的十位数字作为“茎”，个位数字作为“叶”，茎相同者共用一个茎，茎按从小到大的顺序从上向下列出，共茎的叶一般按从大到小（或从小到大）的顺序同行列出.知识点1：利用频率分布直方图分析总体分布例题1： 2000辆汽车通过某一段公路时的时速的频率分布直方图如右图所示，时速在[50,60)的汽车大约有 A ．30辆 B ．60辆 C ．300辆 D ．600辆变式：某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的产品净重（单位：克）数据绘制的频率分布直方图，其中产品净重的范围是 [96，106]，样本数据分组为[96，98），[98，100),[100，102)，[102，104),[104，106],已知样本中产品净重小于100克的个数是36，则样本中净重大于或等于98克并且小于104克的产品的个数是A.90B.75C. 60D.45变式：某初一年级有500名同学，将他们的身高（单位：cm ）数据绘制成频率分布直方图（如图），若要从身高在[)120,130，[)130,140，[]140,150三组内的学生中，用分层抽样的方法选取30人参加一项活动，则从身高在[)130,140内的学生中选取的人数为 ．知识点2：用样本分估计总体例题2某市2010年4月1日—4月30日对空气污染指数的监测数据如下（主要污染物为可吸入颗粒物）:61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,77,86,81,83,82,82,64,79,86,85,75,71,49,45,96 98 100 102 104 106 0.1500.125 0.1000.0750.050 克 频率/组距100 110 120130 140 150 身高频率|组距0.0050.0100.020a0.035(Ⅰ) 完成频率分布表；（Ⅱ）作出频率分布直方图；（Ⅲ）根据国家标准，污染指数在0~50之间时，空气质量为优：在51~100之间时，为良；在101~150之间时，为轻微污染；在151~200之间时，为轻度污染。

频率分布直方图绘制指南频率分布直方图是一种用于可视化数据分布的常见工具。

它能够展示数据集中的值在给定范围内的频率分布情况，帮助我们更好地理解数据的分布特征和趋势。

本文将介绍频率分布直方图的基本概念和绘制方法，帮助你快速掌握绘制直方图的技巧。

什么是频率分布直方图频率分布直方图是一种用矩形条表示数据集中每个值的频率的图表。

它将数据范围划分成若干等距区间，统计每个区间内的数据值数量，并将数量显示为相应的矩形高度。

通过直方图，我们可以观察到数据的分布形状、集中程度和异常值等信息。

绘制频率分布直方图的步骤绘制频率分布直方图的过程通常包括以下步骤：1.确定数据集的范围：首先，需要确定你要绘制直方图的数据集的范围是多少。

根据数据的实际情况，选择一个适当的数据范围确保直方图可以清晰地展示数据的分布情况。

2.将数据划分成区间：通过将数据划分成区间，可以更好地展示数据的分布情况。

根据数据的范围和数量，合理选择区间的数量和等距划分方式。

3.计算每个区间内的频率：统计每个区间内的数据值数量，得到每个区间的频率。

频率可以通过计算每个区间内的数据数量除以总数据量得到。

4.绘制直方图：使用柱状图绘制直方图，即将每个区间的频率作为柱状图的高度，区间的起点作为柱状图的横坐标。

5.添加轴标签和标题：为了提高图表的可读性，添加合适的轴标签和标题，包括横轴标题、纵轴标题和整个图表的标题。

示例假设我们有一个学生年龄数据集，包含了100个学生的年龄信息。

要绘制学生年龄分布的直方图，我们可以按照以下步骤进行：1.确定数据集的范围：观察数据集，确定数据集中最小和最大的年龄值。

假设最小年龄为18岁，最大年龄为22岁。

2.将数据划分成区间：根据数据范围和数量，选择合适的区间数量和划分方式。

这里我们选择5个区间，并采用等宽划分方式。

即，每个区间的宽度为(22 - 18)/5 = 0.8岁。

3.计算每个区间内的频率：统计数据集中落入每个区间内的年龄数量。

庖丁巧解牛知识·巧学一、关于频率分布直方图的概念由于频率分布表数字较多，阅读困难，为了将频率分布表中的结果直观形象地表示出来，我们通常画频率分布直方图.画图时，应以横轴表示分组，纵轴表示频率与组距的比值。

以每个组距为底，以各频率除以组距的商为高,分别画成矩形,这样得到的直方图就是频率分布直方图.二、关于频率分布直方图的绘制方法频率分布直方图是在频率分布表的基础上绘制而成的，它的前期工作就是准确列出频率分布表，然后在平面直角坐标系中画出频率分布直方图，具体步骤如下：（1）求极差，即计算最大值与最小值的差。

(2）决定组距和组数。

组距与组数的确定没有固定标准，需要尝试、选择，力求有合适的组数，以能把数据的规律较清楚地呈现为准.太多或太少都不好,不利对数据规律的发现.组数应与样本的容量有关，样本容量越大组数越多。

(3)决定分点,将数据分组。

分组时，通常规定分组的区间是“左闭右开”的，避免数据被重复计算.（4）列频率分布表。

一般分“分组”“频数”“频率”三列，最后一行是“合计”。

注意频数的合计应是样本容量,频率合计应是1。

（5）画频率分布直方图。

建立直角坐标系，图中横轴为分组，图中的纵轴表示“频率/组距”。

各组数据以小长方形表示，其中，小长方形的宽为组距，小长方形的高=组距频率，频率=样本容量频率=组距×组距频率=小长方体的面积.各小长方形的面积总和为1。

由此可以看出，直方图中的各小长方形的面积表示相应的各组的频率。

这样频率分布直方图就以面积的形式反映了数据落在各个小组的频率的大小.误区警示 直方图中小长方形的高并不表示各组数据的频率，而是频率与组距之比,小长方形的面积才是各组数据的频率.辨析比较 频率分布表在数量表示上比较确切,但不够直观、形象,分析数据的总体态势不太方便,频率分布直方图形象、直观，与频率分布表相比较,频率直方图能直观地表明数据的分布形状,但原始数据不能在图中表示，说明直方图丢失了一些信息.从频率分布直方图可以清楚地看出数据分布的总体态势，但是从直方图本身得不出原始的数据内容。