频率分布直方图
- 格式:doc
- 大小:354.00 KB
- 文档页数:5



频率分布直方图求平均数引言在统计学中,频率分布直方图是一种用于可视化数据集的方法。
它将数据集划分为一系列的区间,称为组或类别,并显示每个组中数据的频率或数量。
频率分布直方图不仅可以帮助我们了解数据的分布情况,还可以帮助我们计算数据的平均数。
本文将介绍如何使用频率分布直方图来计算数据集的平均数。
一、频率分布直方图的定义和构建频率分布直方图是一种以长方形的柱形来表示数据频率或数量的图表。
横轴表示数据的不同组或类别,纵轴表示频率或数量。
频率分布直方图的构建过程通常包括以下步骤:1. 确定组数和组宽:根据数据的范围和分布情况,确定合适的组数和组宽。
组数通常是一个正整数,而组宽则定义了每个组的范围。
2. 组织数据:将数据划分到各个组中。
每个组包含一个范围内的数据值。
3. 计算频率或数量:对于每个组,计算数据在该组内出现的次数或数量。
4. 绘制直方图:使用柱形来表示每个组的频率或数量。
横轴上的刻度表示各个组,纵轴上的刻度表示频率或数量。
二、频率分布直方图的计算平均数的方法频率分布直方图可以帮助我们计算数据集的平均数。
平均数是一个数据集的中心性度量,代表了数据的平均值。
使用频率分布直方图计算平均数的方法如下:1. 确定每个组的中点:对于每个组,计算该组的中点。
中点可以通过该组的上限和下限之间的平均值来计算。
2. 计算组中心的加权平均数:对于每个组,将该组的中点与该组的频率或数量相乘,得到组中心的加权值。
然后将所有组的加权值相加,除以数据集的总频率或数量,得到加权平均数。
三、示例分析为了更好地理解如何使用频率分布直方图来计算数据集的平均数,以下面的数据集为例进行分析:数据集:[1, 2, 3, 3, 4, 5, 5, 6, 7, 8]1. 确定组数和组宽:我们可以选择将数据集划分为4个组,每个组宽为2。
2. 组织数据:将数据划分到各个组中,得到如下分组情况:组1:[1, 2, 3]组2:[3, 4, 5]组3:[5, 6, 7]组4:[7, 8]3. 计算频率或数量:对于每个组,计算数据在该组内的频率或数量:组1:3个数据组2:3个数据组3:3个数据组4:2个数据4. 绘制直方图:根据频率或数量绘制直方图,得到如下图表:组 | 数据频率------------------组1 | ***组2 | ***组3 | ***组4 | **5. 计算平均数:对于每个组,计算该组的中点。


频率分布直方图频率分布直方图是一种常用的统计图表,用于展示数据的分布情况。
它通过将数据分成若干个等距的区间,然后统计每个区间内的数据个数,并将统计结果以柱形图的形式呈现,从而直观地反映数据的分布。
本文将详细介绍频率分布直方图的概念、构建方法、应用场景以及注意事项。
一、频率分布直方图的概念频率分布直方图是一种数据可视化工具,用于展示数据的分布情况。
它将数据划分成若干个等距的区间,然后统计每个区间内的数据个数,最后以柱形图的形式呈现。
每个区间的宽度通常相等,但高度则表示该区间内数据的频数。
频率分布直方图可以帮助人们更好地理解数据的特征,比如中心位置、离散程度和偏态与峰态等。
二、频率分布直方图的构建方法构建频率分布直方图的步骤主要包括:确定划分区间、统计频数、绘制柱形图。
1. 确定划分区间在构建直方图之前,需要确定划分区间的个数和宽度。
划分区间的个数通常由数据的样本量和取值范围决定。
如果样本量较大,可以选择更多的区间,以便更准确地反映数据的细节;反之,如果样本量较小,可以选择较少的区间。
划分区间的宽度应该尽可能相等,以避免误导读者。
常用的划分区间方法有等距划分和等频划分。
等距划分是将整个取值范围等分成若干个区间,如每个区间的宽度为5;等频划分是根据数据的频数将取值范围划分为若干个区间,使每个区间内的频数相等。
2. 统计频数统计频数是指计算每个区间内数据的个数。
可以使用计数器或者计算机软件进行统计。
对于连续数据,需要考虑边界问题,即数据应该分到哪个区间中。
3. 绘制柱形图绘制柱形图是最后一步,通过将每个区间的频数表示为柱形的高度来反映数据的分布情况。
柱形图的横轴表示区间,纵轴表示频数。
每个区间的柱形应该相邻且不重叠。
为了增加可读性,可以在柱形上方标注频数的值。
三、频率分布直方图的应用场景频率分布直方图广泛应用于各个领域,可以帮助人们更好地理解数据的分布情况。
1. 经济学在经济学中,频率分布直方图可以用来展示收入、消费等经济指标的分布情况。




2.2.2频率分布直方图与折线图
【教学内容】
频率分布直方图的定义及绘制,折线图的绘制 【教学要求】
1.使学生了解频率分布直方图的定义及组成
2.掌握画频率法直方图的步骤,能正确画出频率直方图与折线图 【教学重点】
绘制频率直方图、条形图、折线图 【教学难点】
会根据样本频率分布或频率直方图去估计总体分布 【教法】
启发法,讲练结合,讨论式 【教学过程】 一.复习引入 (学生活动)
前面我们已经学过频率分布表,请同学们回答下列问题: 1.总体分布的频率、频数的概念 2.列频率分布表的一般步骤是什么? (引入)我们还学过一种更为直观地体现数据分布规律的方法—绘制频数条形图或频率直方图等。
二.讲授新课 (一)频数条形图
例1.下表是某校一个星期中收来的失物件数,请将5天中
收交来的失物数用条形图来表示。
解:
(二)频率直观图
一般地绘制频率直观图的方法
1.把横轴分成若干段,每一线段对应一个组的组距;
2.然后以此线段为底作一矩形,它的高等于该组的频率/组距;
3.这样得出一系列的矩形,每个矩形的面积恰好是该组上的频率,这些矩形就构成了频率分布直方图。
例2. 我国是世界上严重缺水的国家之一,城市缺水问题较为突出。
某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量标准a ,用水量不超过a 的部分按平价收费,超出a 的部分按议价收费。
如果希望大部分居民的日常生活不受影响,那么a 定为多少比较合理?
分析:先绘制频率分布表,在进行频率直方图的绘制
解:假设通过抽样,我们获得了100位居民的月均用水量(单位:t )
星期 一 二 三 四 五 件数 6 2 3 5 1 累计 6 8 11 16 17
2.6 2.7 2.4 2.1 1.7 1.4 1.2 1.5 0.5 2.4 2.5 2.6 2.3 2.1 1.6 1.0 1.0 1.7 0.8 2.4 2.8 2.5 2.2 2.0 1.5 1.0 1.2 1.8 0.6 2.2
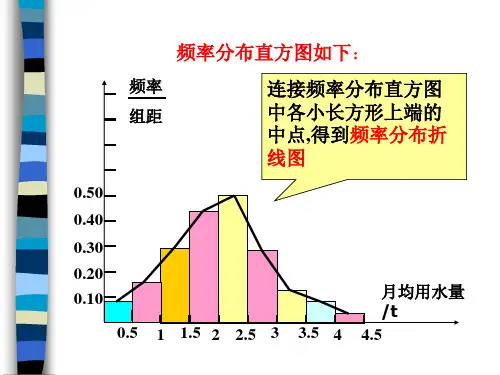
绘制频率分布直方图
从图中我们可以看到,月均用水量在区间[2,2.5)内的居民最多,在[1.5,2)内次之,大部分居民的月均用水量都在[1,3)之间.
说明1:同样一组数据,如果组距不同,横轴、纵轴单位不同,得到的图的性状也会不同。
不同的形状给人不同的印象,这种印象会影响我们对总体的判断,例如说明2:直方图能够很容易地表示大量数据,非常直观地表明分布的形状,使我们能够看到分布表中看不清楚的数据模式,但是直观图也丢失了一些信息,例如,原始数据不能在图中表示出了.
(三).频率折线图
1.如果将频率分布直方图中各相邻的矩形的上底边的中点顺次连结起来,就得到一条折线,我们称这条折线为本组数据的频率折线图.
频率折线图的优点是它反映了数据的变化趋势.如果将样本容量取得足够大,分组的组距取得足够小,则这条折线将趋于一条曲线,我们称这一曲线为总体分布的密度曲线.
组距0.1
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
1471013161922252831343740434649
组距0.1组距1.0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
12345
组距1.0
组距0.5
0.1
0.2
0.3
0.4
0.5
0.6
123456789
组距0.5
组距0.5
0.1
0.2
0.3
0.4
0.5
0.6
123456789
组距0.5
组距0.5
0.1
0.2
0.3
0.4
0.5
0.6
123456789
组距0.5
例3:为了了解一大片经济的生长情况,随机测量其中100株树木的底部周长,得到如下数据表(单位:cm)
135 98 102 110 99 121 110 96 100 103
125 97 117 113 110 92 102 109 104 112
109 124 87 131 97 102 123 104 104 128
105 123 111 103 105 92 114 108 104 102
129 126 97 100 115 111 106 117 104 109
111 89 110 121 80 120 121 104 108 118
129 99 90 99 121 123 107 111 91 100
99 101 116 97 102 108 101 95 107 101
102 108 117 99 118 106 119 97 126 108
123 119 98 121 101 113 102 103 104 108 (1)编制频率分布表
(2)绘制频率分布直方图
(3)估计该片经济林中底部周长小于100cm的树木约占多少,底部周长不小于120cm的树木约占多少?
解:(1)从表中可以看出,这组数据的最大值为135,最小值为80,故全距为55,可将其分为11组,组距为5。
从第1组[80,85)开始,将各组的频数、频率和频率/组距填入表中
三.课时小结
1.频率分布条形图和频率分布直方图
2. 绘制频率直观图的步骤
(注:文档可能无法思考全面,请浏览后下载,供参考。
可复制、编制,期待你的好评与关注)。