2016-2017学年江西省上饶市横峰中学高一上学期期中数学试卷和解析

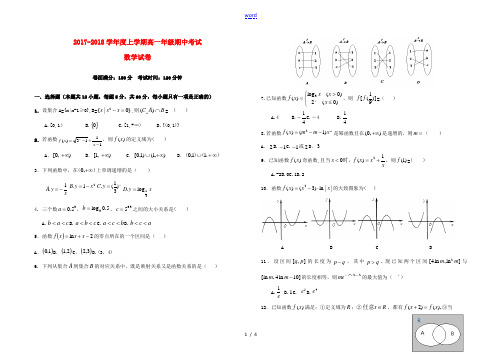
2017-2018学年度上学期高一年级期中考试数学试卷卷面满分：150分 考试时间：120分钟一．选择题（本题共12小题，每题5分，共60分，每小题只有一项是正确的） 1．设集合A={x|x-1≥0},B=}0|{2=-x x x ,则B A C R ⋂)(= ( )A.[0,1）B.{}0C.[1,+∞)D.{(0,1)}2．若函数1113)(-+-=x x f x ，则)(x f 的定义域为( )A ．),0[+∞B ．),1[+∞C ．),1()1,0[+∞⋃D ．），（）（∞+⋃11,0 3．下列函数中，在）（+∞,0上单调递增的是（ ） x y A 1.-=21.x y B -=xy C )31(.=x y D 21log .= 4. 三个数35.0=a ，5.0log 3=b ，3.05=c 之间的大小关系是( )A.c a b <<B.c b a <<C.b c a <<D.a c b << 5．函数()2ln -+=x x x f 的零点所在的一个区间是（ ） A ．()1,0B ．()2,1C ．()3,2 D.(3，4)6. 下列从集合A 到集合B 的对应关系中，既是映射关系又是函数关系的是（ ）7.已知函数⎩⎨⎧≤>=)0(2)0(log )(3x x x x f x，则 )]91([f f =（ ） A.4 B.41-C.－4D.418.若函数mx m m x f )1()(2--=是幂函数且在(0,)+∞是递增的，则m =（ ） A ．2B.1- C.1-或2D ．39．已知函数)(x f 奇函数,且当xx x f x 1)(02+=<时，，则)1(f =( ) A.-2B.0C.1D.210．函数||ln )3()(2x x x f ⋅-=的大致图象为( )A B C D11．设区间[,]q p 的长度为p q -，其中p q >.现已知两个区间2[4ln ,ln ]m m 与[ln ,4ln 10]m m -的长度相等，则222-+-x xme 的最大值为（ `）A.e1 B.1C. 5e D.4e 12．已知函数)(xf 满足：①定义域为R ；②R x ∈任意，都有),()2(x f x f =+③当1||)(]1,1[+-=-∈x x f x 时，都有，则方程|1|log 21)(2-=x x f 在区间[-3,5]所有的解的和是（ ）A.5B.13C.14D.6二．填空题（本题共4小题，每小题5分，共20分）13．设函数)9(log )(23x x f -=集合)}(|{x f y x A ==，集合)}(|{x f y y B ==，则阴影部分表示的集合为_____________.14．若点)2,3(在函数)3(log )(5m x f x -=的图象上，则函数mx y -=1的最大值为 .15.设定义在]3,4[-a 上的偶函数)(x f ，当0≥x 时，)(x f 单调递减，若)2()2(m f m a f <-成立，则m 的取值X 围是.16.对于函数)(x f 与)(x g ，若存在}0)({=∈∈x f R x λ，}0)({=∈∈x g R x μ，使得1≤-μλ，则称函数)(x f 与)(x g 互为“零点密切函数”，现已知函数3)(2-+=-x e x f x 与4)(2+--=x ax x x g 互为“零点密切函数”，则实数a 的取值X 围是__________．三．解答题（本题共六小题，共计70分）17．(本小题10分)（1）132103410.027()2563(21)7-----+-+-；（2）14lg 2lg 5lg 2lg 2lg 22+-+⋅+．18.(本小题12分)已知集合}31|{≥-≤=x x x A 或，{}23B x a x a =≤≤+，求下列条件下的实数a 的取值X 围．（1）若1=a ，试求B A C R ⋃)(,)(B C A R ⋂ （2）若A ∩B ＝B ，某某数a 的取值X 围．19.(本小题12分)已知函数121)(+-=xa x f . （1）确定a 的值, 使)(x f 为奇函数；（2）当)(x f 为奇函数时，用定义证明函数)(x f ),(+∞-∞在内是增函数.20. 已知函数)3(log )1(log 22++-=x x y （1）求函数的定义域，判断函数的奇偶性. （2）求函数的值域.21.(本小题12分）某公司试销一种成本单价为400元/件的新产品，规定试销时销售单价不低于成本单价，又不高于800元/件，经试销调查，发现销售量y (件)与销售单价x (元/件)可近似看作一次函数y ＝kx ＋b 的关系(如图所示)． (1)根据图象，求一次函数y ＝kx ＋b 的表达式；(2)设公司获得的毛利润(毛利润＝销售总价－成本总价)为S 元．试用销售单价x 表示利润S ；并求销售单价定为多少时，该公司可获得最大毛利润？最大毛利润是多少？此时的销售量是多少？22．(本小题12分)已知二次函数)(x f 满足不等式25)(-<x x f 的解集是)2,1(，且)(x f 的图像过点)1,1(--．记函数⎩⎨⎧≤->=0),(0,log )(2x x f x x x g ．（Ⅰ）求()f x 的解析式，写出函数)(x f y =的单调递减区间. （2）画出)(x g 的图像.（3）求关于x 的方程01)(3)(22=+-x g x g 不同的根的个数．2017-2018学年度上学期高一年级期中考试数学答案13. }3|{≥x x 14.1 15.41<m 16.43≤≤a17.(1)17................5分 （2）1................10分}41|{)(1.18≤<-=⋃x x B A C R ）（,...............4分 4}x 1x |{x )(>-<=⋂或B C A R ...............6分分或分或解得或，则若分，则若）（12...........3410.. (2)34,32138...........3,,2->-<>-<>-<+∅≠->∅==⋂a a a a a a B m B B B A ...............12分19 (1)由题意，得x ∈R ，即函数的定义域关于原点对称，f (－x )＝12－112x ＋1＝12－2x2x ＋1＝1－2x22x＋1＝－12＋12x ＋1＝－f (x )， ∴函数f (x )为奇函数．..............6分(2)设x 1，x 2是(－∞，＋∞)内任意两实数，且x 1<x 2， 则f (x 1)－f (x 2)＝12－12x 1＋1－12＋12x 2＋1＝2x1－2x22x 1＋12x2＋1∵x 1<x 2，∴2x1－2x2<0，∴f (x 1)－f (x 2)<0， ∴函数f (x )在(－∞，＋∞)内是增函数．函数f (x )在(－∞，＋∞)内是增函数，..............12分 20.解：（1）,13,0301<<-⎩⎨⎧>+>-x x x 解得.............4分，定义域不对称，非奇非偶函数.............6分分（即（分为增函数在分令）（12].......2,],4log ,10.......]4,0(log 8.......4)1(],4)1([log 222222∞-∈∞-∈∴∈=++-=++-=y y t t y x t x y21.解：(1)由图象知，当x ＝600时，y ＝400； 当x ＝700时，y ＝300.代入y ＝kx ＋b 中，得⎩⎪⎨⎪⎧400＝600k ＋b 300＝700k ＋b 解得⎩⎪⎨⎪⎧k ＝－1b ＝1 000∴y ＝－x ＋1 000(500≤x ≤800)........6分(2)销售总价＝销量单价×销售量＝xy ，成本总价＝成本单价×销售量＝500y ， 代入求毛利润的公式，得S ＝xy －400y ＝x (－x ＋1 000)－400(－x ＋1 000)＝1 2 3 4 5 6 7 8 9 10 11 12 BCAABCDABBDD－x 2＋1 400x －400 000＝－(x －700)2＋90000(400≤x ≤800)∴当销售单价为700元/件时，可获得最大毛利润90000元，此时销售量为300件.............12分22.解：(1)①由条件可设)0(25)2)(1()(>-+--=a x x x a x f 又因为)(x f 的图像过点)1,1(--，所以1=a 所以x x x f 2)(2+=．………3分 减区间为:)0,1(),2,(---∞………5分 ②)(x g 图像………8分(2)设()x g t =，则函数01322=+-t t ，21=∴t 或1=t 即21)(=x g 或1)(=x g ，由(1)图像可知方程21)(=x g 有4个不同根,方程1)(=x g 有3个不同根.从而所求方程共有7个不同的根．………12分。

横峰中学2015-2016学年度上学期期中考试高一年级数学试卷一、选择题（每题5分，共60 分）1．已知集合，{|,,}B z z x y x A y A==+∈∈，则( )A． B． C． D．2．函数y＝的定义域是（）A．[－1，＋∞） B．[－1,0） C．（－1，＋∞） D．（－1,0）3．下列四组函数，表示同一函数的是（）.A．,B．,C．,D．,4.函数y=x+2(m-1)x+3在区间上是单调递减的，则m的取值范围是( )A. m3B. m3C. m-3D. m-35．已知幂函数的图象经过点（4，2），则（）A.2B.4C.4D.86．已知a＝，b＝，，则a，b，c三者的大小关系是( )A．b>c>a B．b>a>c C．a>b>c D．c>b>a7．把函数的图象向左平移2个单位，再向上平移3个单位，所得图象的函数关系式为（）（A）（B）（C）（D）8．函数的定义域为R，且满足若等于（）A．-9 B．9 C．-3 D．09．已知函数为定义在上的偶函数，则的值是（）A. B. C. 或 D. 或10．函数的值域是（）A． B． C．D．11．已知是定义在R上的函数，且恒成立，当时，，则当时，函数的解析式为（）A． B． C． D．12．偶函数f (x)满足f(x-1)=f(x+1),且在x ∈[0,1]时,f(x)=x,则关于x 的方程f(x)=()x 在x ∈[0,4]上解的个数是( )(A)1 (B)2 (C)3 (D)4 二、填空题（每题5分，共20分）13．已知集合，集合},01{2R ∈≤-=x x x B ，则_______．14．函数的图象与的图象关于y 轴对称，则函数的递增区间是_________． 15函数3222)1(----=m m xm m y 是幂函数，且当x ∈(0，＋∞)时为减函数，则m ＝________.16．对于定义在R 上的函数，若实数满足，则称是函数的一个不动点。

2016—2017学年江西省上饶市横峰中学高一（上）期中物理试卷一、选择题:(本题包括12小题，共48分．其中1-7题每小题只有一个正确答案,选对得4分；8—12题为不定项选择题，每小题有一个或一个以上正确答案，每小题4分，选对但不全的得2分，错选得0分．）1．以下的计时数据指的是时间间隔的是（）A．中央电视台新闻联播节目在北京时间19：00准时开播B．某同学跑1500m用时5:04C．1997年7月1日零时中国对香港恢复行使主权D．我们学校早上第四节课的上课时间是10：35～11：152．在某段公路上，分别有图示的甲、乙两块告示牌，告示牌上面数字的意思是(）A．甲是指位移,乙是平均速度B．甲是指路程,乙是平均速度C．甲是指位移，乙是瞬时速度 D．甲是指路程,乙是瞬时速度3．现代战争是科技之战、信息之战，某集团军进行的一次实战演习过程,在基地导演部的大型显示屏上一览无余，如图1所示是蓝军由基地A分三路大军进攻红军基地B的显示，若用x1、x2和x3分别表示三路大军的位移，则由大屏幕的显示图可知（)A．x1＞x2＞x3B．x1＜x2＜x3C．x1=x2=x3D．三者关系无法确定4．沿直线运动的一列火车和一辆汽车，在计时开始时及每过1s时火车和汽车的速度分别为v1和v2如表所示，由表中数据可看出（）t/s 0 1 2 3 …v1/m•s﹣115.0 15.3 15.6 15。

9 …v2/m•s﹣120 18 16 14 …A．火车的位移在增大,汽车的位移在减小B．火车的位移在减小，汽车的位移在增大C．火车的速度变化大，汽车的速度变化小D．火车的速度变化慢，汽车的速度变化快5．物体做匀加速直线运动，已知t=1s时速度为6m/s，t=2s时的速度为8m/s，下列说法中正确的是(）A．计时起点t=0时的速度为0 m/sB．物体的加速度为6m/s2C．任意1秒内的速度变化2m/sD．第1秒内的平均速度为6m/s6．一物体做自由落体运动，自由下落L时，速度为v,当物体自由下落的速度速度达到时，它下落的长度是（)A．B．C．D．7．关于自由落体运动,下列说法不正确的是(）A．物体竖直向下的运动一定是自由落体运动B．自由落体运动是初速度为零，加速度为g的竖直向下的匀加速直线运动C．物体只在重力作用下从静止开始下落的运动叫做自由落体运动D．当空气阻力的作用比较小，可以忽略不计时，物体的自由下落可看成自由落体运动8．一辆汽车由静止开始做匀加速运动，经ts速度达到υ，立即刹车做匀减速运动,又经2ts 停止,则汽车在加速阶段与在减速阶段（）A．速度变化量的大小相等 B．加速度的大小相等C．位移的大小相等D．平均速度的大小相等9．一个运动的物体，若其加速度逐渐减小到零，则物体的运动速度可能(）A．逐渐减小 B．逐渐增大 C．先减小后增大 D．先增大后减小10．甲、乙两球从同一高处相隔1s先后自由下落,在下落过程中（）A．两球速度差始终不变B．两球速度差越来越大C．两球距离始终不变 D．两球距离越来越大11．物体甲的x﹣t象和物体乙的v﹣t别如图所示，则这两个物体的运动情况是(）A．甲在整个t=6s时间内来回运动,它通过的总位移为零B．甲在整个t=6s时间内运动方向一直不变,它通过的总位移大小为4mC．乙在整个t=6s时间内来回运动,它通过的总位移为零D．乙在整个t=6s时间内运动方向一直不变，它通过的总位移大小为4m12．完全相同的三块木板并排固定在水平面上,一颗子弹以速度v水平射入,若子弹在木块中做匀减速直线运动，且穿过第三块木块后子弹速度恰好为零,则子弹依次刚射入每块木块时的速度之比和穿过每块木块所用的时间之比分别是(）A．v1：v2：v3=3:2：1 B．v1：v2：v3=：：1C．t1:t2:t3=(﹣）：(﹣1）:1 D．t1：t2：t3=1：:二、实验题与填空题（共12分，13题每空2分,14题每空1分）13．如图所示，是某同学打下的一条匀加速直线运动的纸带，相邻的两个计数点间还有4个点未画出，打点计时器使用的是50Hz的交流电．计数点间的距离依次为S1=2.60cm、S2=4.10cm、S3=5。

横峰中学2015-2016学年度上学期第一次月考高三数学（文科）试卷出卷老师：宋争丁 （时刻：120分钟 满分：150分）一、选择题：本大题共12小题，每小题5分，共60分． 1．设集合}032{2<--=x x x M ，集合{})2ln(-==x y x N ，则=M N C R )( ( )A ．}21{<≤-x x B ．}23{≤<-x x C ．}21{≤<-x xD ．}32{<<x x2．在等差数列}a {n 中，已知前15项的和90S 15=，则=8a （ ） A ．245B ．6C ．445D ．123．下列函数中，既是偶函数又在()∞+,0单调递增的函数是（ ）A ．3y x =B ．||1y x =+C ．12+-=x y D ．xy -=24．设α是第二象限角，)4,(x P 为其终边上的一点，且x51cos =α，则=αtan （ ）A ．34B ．43C ．43-D ． 34-5．已知()f x 在R 上是奇函数，且)()2(x f x f -=+，当)2,0(∈x 时，12)(-=x x f ，则=)2015(f （ ）A ．2-B ．1-C ．4-D ．2015- 6．下列命题中正确的有（ ） ①命题”Rx ∈∃0，02031x x >+”的否定是”R x ∈∀，x x 312≤+” ②”0652=--x x ”是”1-=x ”的必要不充分条件 ③若”q p 且”为假命题，则p ，q 均为假命题；④”平面向量→a 与→b 的夹角是钝角”的充分没必要要条件是”0<⋅→→b a ”A ．①B ．①②C ．①②③D ．①②④ 7．若0.53,ln 2,log sin12a b c ππ===，则（ ）A ．b a c >>B ．a b c >>C ．c a b >>D ．b c a >>8．平面向量→a 与→b 的夹角为120，)0,2(=→a ，1=→b ，则=+→→b a 2（ ）A ．2B ．32C ．4D ．69．已知命题p ：R x ∈∀，xx32<；命题q ：R m ∈∃，使342)1()(+--=m m x m x f 为幂函数，且在),0(+∞上递减，则下列命题中为真命题的是（ ）A ．q p 且B ．q p 且非C ．)(q p 非或D ．)()(q p 非且非10．函数)sin()(ϕω+=x A x f （其中0>A ，0>ω，2πϕ<）的图象如图所示，为了取得()cos2g x x =的图象，则只要将()f x 的图象（ ）A ．向右平移6π个单位长度B ．向右平移12π个单位长度 C ．向左平移12π个单位长度D ．向左平移6π个单位长度11．若点M 是ABC ∆所在平面内的一点，且知足3=--AC AB AM ，则ABM ∆与ABC∆面积之比等于（ ）A ．31B ．43C ．41D ． 2112．设概念在R 上的函数⎪⎩⎪⎨⎧=≠-=21221)(x x x x f ，若关于x 的方程2()()0f x af x b ++=有5个不同的实数根，则a 的取值范围为（ ） A ．)1,2()2,(--⋃--∞ B ．)1,0(C ．)1,(--∞D ．),1(+∞二、填空题：(本大题共4小题，每小题5分，共20分)．13．设平面向量)2,1(=→a ，),2(mb -=→，若→→b a //，则=m ． 14．已知等差数列{}n a 首项01>a ，n S 为数列{}n a 的前项和，且136S S =，则当n S 取得最大值时n 的值为 ．15．若→a 与→b 为两个单位向量，且23)(=+⋅→→→b a a ，记→a 与→b 的夹角为θ，则函数)6sin(πθ+⋅=x y 的最小正周期为 ．16．已知函数xx x x f cos 43sin 4121)(--=的图像在点),(00y x A 处的切线的斜率为1，则=0tan x ．三、解答题（本大题共6小题，满分70分，解承诺写出文字说明、证明进程或演算步骤） 17．（本小题满分10分）在数列{}n a 中，111,n n a a a c +==+（c 为常数，n ∈N *），且125,,a a a 成公比不等于1的等比数列（1）求c 的值；（2）设11n n n b a a +=，求数列{}n b 的前n 项和n S18．（本小题满分12分）已知函数xx x x f sin cos )12cos 2(sin )(2⋅+-=θ（0＜θ＜π）在π=x 处取最小值．（1）求θ的值；（2）若31)32(=-πx f ，且),43(ππ∈x ，求x 2sin 的值．19．（本小题满分12分）数列{}n a 的前n 项和为n S ,点(,)n n P s a 在直线01=-+y x 上，数列{}n b 知足nn a b 21log =，（1）求数列{}n a 及{}n b 的通项公式；（2）令nnn a b c =，n T 为数列{}n C 的前n 项和，求n T .20．（本小题满分12分）在ABC ∆中，A 、B 、C 对边别离是a 、b 、c ， 且知足(2)cos cos a c B b C -=（1）求B 的大小；（2）设(sin ,cos 2),(4,1)(1)m A A n k k ==>，且m n ⋅的最大值是5，求k 的值.21．（本小题满分12分）已知函数()ln(1)(1)1f x x k x =---+（k ∈R ），（备注：1[ln(1)]')1x x -=- （1）求函数()f x 的单调区间；（2）若()0f x ≤恒成立，试肯定实数k 的取值范围.22．（本小题满分12分）设函数x b ax x x f 22333)(+-= ),(R b a ∈（1）若0,1==b a ，求曲线)(x f y =在点))1(,1(f 处的切线方程；（2）若b a <<0，不等式)()1ln 1(x kf x x f >-+对任意),1(+∞∈x 恒成立，求整数k 的最大值．。

江西省横峰中学2015-2016学年高一下学期期中考试数学试题考试用时： 120分钟 总分：150分第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.下列命题正确的是（ ）A ．第二象限角必是钝角B ．相等的角终边必相同C ．终边相同的角一定相等D ．不相等的角终边必不相同 【答案】B 【解析】试题分析：根据终边相同的角应相差周角的整数倍，举反例或直接进行判断.选项A ，如480120︒︒和的角终边相同，都是第二象限角，但480︒不是钝角，故错误； 选项B ，因为角的始边放在X 轴的非负半轴上，则相等的角终边必相同，故正确； 选项C ，终边相同的角应相差周角的整数倍，而不是相等，故错误； 选项D ，如480120︒︒和的角不相等，但是它们终边相同，故错误； 考点：象限角、轴线角.2.与－460°终边相同的角可表示为（ ） A ．k·360°＋100°（k ∈Z ） B ．k·360°＋433°（k ∈Z ） C. k·360°＋260°（k ∈Z ） D ．k·360°－260°（k ∈Z ）【答案】C 【解析】试题分析：由460=2360260-︒-⨯︒+︒，可得260︒和460-︒终边相同，因此可得与角460-︒终边相同的角一定可以写成()360260k k Z ︒+︒∈的形式.故选C. 考点：终边相同的角的定义和表示方法. 3.函数⎪⎭⎫⎝⎛+=43tan πx y 的最小正周期为（ ） A ．3π B ． π3 C ． 32π D ．π6【答案】B 【解析】试题分析：由函数()tan y A x ωϕ=+的图象与性质可得，函数⎪⎭⎫ ⎝⎛+=43tan πx y 的最小正周期为313T ππ==.故选B.考点：函数()tan y A x ωϕ=+的图象与性质.4.已知向量与反向，下列等式中成立的是（ ）A ．||||||-=-B ．||||-=+C ．||||||+=+D ．||||||-=+ 【答案】D 【解析】试题分析：因为非零向量反向，所以根据向量的加法法则可知，.故选D.考点：向量的概念及几何表示.5.己知12112),(,e R e e e =∈+=≠λλ ,则a 与b 共线的条件为( )A. 0=λB. 02=eC. 21//e eD. 21//e e 或0=λ 【答案】D 【解析】试题分析：若,a b 共线，则存在m 使a mb =，即1212e e m e λ+=，所以当,a b 共线时，有=0λ或12e e .故选D.考点：向量共线的充要条件及坐标表示. 6.已知函数()sin,()tan()2x f x g x x ππ+==-，则（ ） A ．()f x 与()g x 都是奇函数 B ．()f x 与()g x 都是偶函数C ．()f x 是偶函数，()g x 是奇函数D ．()f x 是奇函数，()g x 是偶函数【答案】C 【解析】试题分析：因为()sincos 22x xf x π+==，()()tan tang x x x π=-=-，所以()()cos cos 22x x f x f x ⎛⎫-=== ⎪⎝⎭，是偶函数；()()()tan tan g x x x g x -=--==-，是奇函数.故选C.考点：两角和与差的三角函数及三角恒等变换. 7.函数)32cos(π+=x y 的图象的一条对称轴方程是（ ）A ．2π-=x B. 4π-=x C. π=x D. 6π-=x【答案】D考点：余弦函数的图像及性质.8.如果21)cos(-=+A π，那么=+)2sin(A π（ ） Ａ. 21-Ｂ. 23 Ｃ. 23- Ｄ.21【答案】D 【解析】试题分析：因为()1cos cos 2A A π+=-=-，解得1cos 2A =；所以1sin cos 22A A π⎛⎫+== ⎪⎝⎭.故选D.考点：三角函数诱导公式.9.如图，曲线对应的函数是 （ ）A ．y=－sin|x |B ．y=sin|x |C ．y=|sin x |D ．y=－|sin x |【答案】A 【解析】试题分析：应用排除法解决问题，先从图像的右侧观察知它与正弦曲线一样，可排除一些选项，再从左侧观察又可排除一些，从而可选出答案.观察图像知，在y 轴的右侧，它的图像与函数sin y x =-相同，排除B ，C ；在y 轴的左侧，它的图像与函数sin y x =相同，排除D ；故选A.考点：三角函数的图像和图像变换.10.设250cos 1 -=a ，13tan 113tan 22-=b ，,4sin 234cos 21 -=c 则有（ ） A.a b c >> B.a b c << C.a c b << D.b c a << 【答案】C 【解析】试题分析：因为sin 25a ==︒，22tan13tan 261tan 13b ︒==︒-︒，1cos 44sin 30cos 4cos30sin 4sin 262c =︒︒=︒︒-︒︒=︒，sin 25sin 26tan 26︒<︒<︒，所以a c b <<.故选C.考点：三角函数的基本关系式. 11.函数)23sin(x y -=π的单调递减区间是（ ）A.;32,6Z k k k ∈⎥⎦⎤⎢⎣⎡+-+-ππππ B.;1252,122Z k k k ∈⎥⎦⎤⎢⎣⎡+-ππππ C.;125,12Z k k k ∈⎥⎦⎤⎢⎣⎡+-ππππ D.;3,6Z k k k ∈⎥⎦⎤⎢⎣⎡+-ππππ 【答案】C 【解析】试题分析：因为sin 2sin 233y x x ππ⎛⎫⎛⎫=-=--⎪ ⎪⎝⎭⎝⎭，所以函数的单调递减区间为()222232k x k k Z πππππ-≤-≤+∈，，即5,1212k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦.故选C. 考点：三角函数的诱导公式；正弦函数的图像和性质. 12.给出下列命题：其中正确命题的序号是（ ）①已知)2,3(),1,1(),2,1(-==--=c b a ,若b q a p c +=,则p =1, q =4②不存在实数α,使1cos sin =αα ③ ⎪⎭⎫⎝⎛0,8π是函数)452sin(π+=x y 的一个对称轴中心④已知函数()f x ()中，上为减函数，在锐角在ABC ∆1,0)(cos )(sin C f A f <有. A ．①② B ．②④ C ．①③ D ． ④ 【答案】B 【解析】 试题分析：①由题意得()()(),2,3,2p p q q --+=-，即322q p q p -=⎧⎨-=-⎩，解得58p q =⎧⎨=⎩.故错误；②因为1sin cos sin 12ααα==，即sin 2α=不存在，所以正确； ③因为函数)452sin(π+=x y 的对称中心为(),0k π，即()52,4x k k Z ππ+=∈,解得528k x ππ=-；当1k =时，8x π=-；所以,08π⎛⎫- ⎪⎝⎭是函数的一个对称中心.故错误； ④因为在锐角三角形中，2A C π+>，所以022A C ππ>>->，022C A ππ>>->；则有1sin sin cos 02A C C π⎛⎫>>-=> ⎪⎝⎭，1sin sin cos 02C A A π⎛⎫>>-=> ⎪⎝⎭；又因为函数()f x 在()0,1上为减函数，所以(sin )(cos )f A f C <.故正确.考点：向量的线性运算；三角函数的基本关系式；函数的图像和性质.第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13.已知正方形ABCD 的边长为1, =a , =b , =c ,则|a +b +c |等于 【答案】22. 【解析】试题分析：由向量加法的三角形法则可得：222a b c AB BC AC AC AC AC ++=++=+==考点：向量的加法；向量的模. 14.)(1)23(,)(x f x f x x f -=+π均有满足：对任意的函数,当[]ππ,-∈x 时，x x x f s i n )(=，则()________5.8=-πf【答案】2π. 【解析】试题分析：因为3311(3)()()3122()2()f x f x f x f x f x ππππ+=++=-=-=+-，所以函数是周期为3π的周期函数；则()()()8.590.50.5sin222f f f πππππππ-=-+===.考点：函数的周期性.15.B A B A ABC cos cos sin sin <∆中，若满足,则的形状为ABC ∆______________ 【答案】钝角三角形. 【解析】试题分析：因为()sin sin cos cos cos 0A B A B A B -=-+<，所以()()cos cos cos 0A B C C π+=-=->，则cos 0C <，得2C ππ<<，由此可得ABC ∆为钝角三角形.考点：两角和的余弦公式；余弦函数的诱导公式；任意角三角函数在各象限的符号. 16.设函数))((R x x f ∈满足),()(x f x f =- ),2()(x f x f -=且当]1,0[∈x 时,,)(3x x f =又函数πcos(|)(x x g =|)x ,则函数)()()(x f x g x h -=在]23,21[-上的零点个数为 _____________ 【答案】6. 【解析】试题分析：要确定函数在上的零点个数，即求图象交点个数.因为，所以函数f(x)是偶函数，()()2f x f x -=-,()()2f x f x =+,函数周期为2.∵当x ∈[0,1]时，()3f x x =； ∴当x ∈[-1,0]]时，()3f x x =；∴当[]1,2x ∈时，[]20,1x -∈，()()()322f x f x x =-=-；又()()cos g x x x π=，()()g x g x -=，所以()g x 是偶函数；∴当102x ⎡⎤∈-⎢⎥⎣⎦，时， ()()cos g x x x π=； ∴当10,2x ⎡⎤∈⎢⎥⎣⎦时， ()()cos g x x x π=； ∴当13,22x ⎡⎤∈⎢⎥⎣⎦时， ()()cos g x x x π=-； ∵()()00f g =，()()11=1f g =，13022g g ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭，在同一坐标系内画出函数在上的简图，观察图像：除了0,1这两个零点之外，分别在区间102⎡⎤-⎢⎥⎣⎦，，12⎡⎤⎢⎥⎣⎦0，，12⎡⎤⎢⎥⎣⎦，1，32⎡⎤⎢⎥⎣⎦1，上各有一个零点，∴)()()(x f x g x h -=在上的零点个数有6个.考点：函数零点个数的判断.三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） 17.（本小题满分10分）平面内给定三个向量: a = (3, 2), b = (-1, 2), c = (4, 1).(1)求c b a 23-+;(2)若)2//()(k -+, 求实数k 的值. 【答案】(1) (0, 6 )； (2) 1316-=k .【解析】试题分析： (1)根据平面向量的坐标运算的法则即可求得；（2）运用向量平行的条件，将其转化为关于坐标的等式求解.考点：平面向量的坐标运算；平面向量平行的充要条件. 18.（本小题满分10分）已知角α终边上一点P （－3，4），求： （1）的值和ααcos sin（2）)29sin()211cos()sin()2cos(απαπαπαπ++----+的值。

江西省横峰中学2017-2018学年度上学期高一第一次月考数学试卷1.已知集合，则下列式子表示不正确的是（）A. B. C. D.【答案】B【解析】由知，A,C,D选项正确，B选项错误，因为集合与集合关系不是属于关系，故选B.2.集合，则（）A. B. C. D.【答案】D【解析】因为，所以，故选D.3.下列各组函数的图象相同的是（）A.B. 与g（x）=x+2C.D.【答案】D【解析】试题分析：A．两个函数的定义域不相同，B．同样是两个函数的定义域不相同，，，C．同样是两个函数的定义域不相同，的定义域是，D．函数，两个函数的定义域相同，化简后的解析式也相同，所以是同一函数，故选D．考点：函数的表示方法4.已知映射，在映射下的原象是（）A. B. C. D.【答案】B【解析】由解得，故映射的原象为，故选B.5.下列函数中,在区间上是增函数的是（）A. B. C. D.【答案】A【解析】当时，，是增函数，且，所以函数是偶函数，故选A.6.若函数的定义域为，则函数的定义域是（）A. B. C. D.【答案】B【解析】试题分析：根据已知可得函数的定义域需满足：解得，即函数定义域为，故选择B考点：求函数定义域7.已知在上是单调递增的，且图像关于轴对称，若，则的取值范围是（）A. B.C. D.【答案】D【解析】因为函数是偶函数，所以，又在上是单调递增的，所以，解得，故选D.8.幂函数在为减函数，则的值为（）A. 1 或3B. 1C. 3D. 2【答案】C【解析】试题分析：由幂函数的定义知，其中是自变量，是常数．所以．当时，在R上为单调递增函数，不满足题意；当时，，在上为减函数，满足题意，故选C．考点：1、幂函数的意义；2、幂函数的性质．9.已知，则的解析式可取为（）A. B. C. D.【答案】C【解析】令，则，所以，故，故选C.10.函数的最小值为（）A. 2B. 3C. 2D. 2.5【答案】D【解析】因为，令，则是增函数，所以当时，有最小值2.5，故选D.11.设函数，若互不相等的实数，，满足，则++的取值范围是（）A. （，B. [，6C. （，6）D. （，）【答案】C【解析】函数图象如图，不妨设x1＜x2＜x3，则x2，x3关于直线x=3对称，故x2+x3=6，且x1满足，则x1+x2+x3的取值范围是：，故选C12.设满足，且在上是增函数，且，若函数对所有的，当时都成立，则的取值范围是（）A. B. 或或C. 或或D.【答案】B【解析】若函数对所有的都成立，由已知易得的最大值是1，∴，设，欲使恒成立，则或或，故选B.13.偶函数f(x)的图象关于直线x＝3对称，f(5)＝10，则f(－1)＝________.【答案】10【解析】的图象关于直线x=3对称，且，则，是偶函数，所以．故答案为：．14.函数的增区间为。

2016-2017学年江西省上饶市横峰中学高一（上）期中数学试卷一、选择题：（本题包括12小题，共60分，每小题只有一个选项符合题意）1．（5分）设f（x）=，则f（f（﹣2））的值为（）A．3 B．6 C．9 D．122．（5分）集合A={y|y=}，B={x|log2（x﹣2）≤1}，则A∩B（）A．[1，4]B．[0，4]C．[0，2]D．（2，4]3．（5分）已知a＞0且a≠1，下列四组函数中表示相等函数的是（）A．与y=2log a x B．y=2x与C．与D．与y=x4．（5分）下列函数中，是偶函数，且在区间（0，1）上为增函数的是（）A．y=|x|B．y=3﹣x C．y= D．y=﹣x2+45．（5分）若函数y=f（x）的定义域是[0，2]，则函数g（x）=的定义域是（）A．[0，1]B．[0，1） C．[0，1）∪（1，4]D．（0，1）6．（5分）已知a=log0.60.5，b=ln0.5，c=0.60.5．则（）A．a＞b＞c B．a＞c＞b C．c＞a＞b D．c＞b＞a7．（5分）已知f（x）在（﹣∞，0]上是单调递增的，且图象关于y轴对称，若f（x﹣2）＞f（2），则x的取值范围是（）A．（﹣∞，0）∪（4，+∞）B．（﹣∞，2）∪（4，+∞）C．（2，4）D．（0，4）8．（5分）幂函数f（x）=（m2﹣4m+4）x在（0，+∞）为减函数，则m 的值为（）A．1或3 B．1 C．3 D．29．（5分）已知函数f（x）=（x﹣a）（x﹣b）（其中a＞b），若f（x）的图象如图所示，则函数g（x）=a x+b的图象大致为（）A．B．C．D．10．（5分）已知定义在R上函数f（x）=对任意x1≠x2都有（x1﹣x2）[f（x1）﹣f（x2）]＜0，那么a的取值范围是（）A．（0，1） B．（0，）C．[，）D．[，1）11．（5分）已知函数f（x）=，若关于x的方程f（x）=k有两个不等的实根，则实数k的取值范围是（）A．（0，+∞）B．（﹣∞，1）C．（1，+∞）D．（0，1]12．（5分）设f（x）满足f（﹣x）=﹣f（x），且在[﹣1，1]上是增函数，且f（﹣1）=﹣1，若函数f（x）≤t2﹣2at+1对所有的x∈[﹣1，1]，当a∈[﹣1，1]时都成立，则t的取值范围是（）A．﹣≤t≤B．﹣2≤t≤2C．t≥或t≤﹣或t=0 D．t≥2或t≤﹣2或t=0二、非选择题：（本题包括4小题，共20分）13．（5分）函数y=f（x）图象与函数y=log a x图象关于直线y=x对称，则函数y=f （x﹣1）图象过定点．14．（5分）函数f（x）=（x2﹣6x+5）的单调递减区间是．15．（5分）若函数y=x2﹣3x﹣4的定义域为[0，m]，值域为[﹣，﹣4]，则m 的取值范围是．16．（5分）已知集合A={（x，y）|y=0.2|x|﹣1}，集合B={（x，y）|y=m}，若A ∩B≠∅，则实数m的取值范围是．三、解答题：本大题共6小题，解答应写出文字说明，证明过程或演算步骤17．（10分）计算下列各式的值：（1）﹣（）0+（）﹣0.5+；（2）lg500+lg﹣lg64+50（lg2+lg5）2．18．（12分）已知集合A={x|（x﹣a）[x﹣（a+3）]≤0}（a∈R），B={x|x2﹣4x ﹣5＞0}．（1 ）若A∩B=∅，求实数a的取值范围；（2 ）若A∪B=B，求实数a的取值范围．19．（12分）已知定义在R上的奇函数f（x），当x＞0时，f（x）=﹣x2+2x （Ⅰ）求函数f（x）在R上的解析式；（Ⅱ）若函数f（x）在区间[﹣1，a﹣2]上单调递增，求实数a的取值范围．20．（12分）已知定义在R上的函数f（x），对任意a，b∈R，都有f（a+b）=f （a）+f（b）﹣1，当x＞0时，f（x）＞1；且f（2）=3，（1）求f（0）及f（1）的值；（2）判断函数f（x）在R上的单调性，并给予证明；（3）若f（﹣kx2）+f（kx﹣2）＜2对任意的x∈R恒成立，求实数k的取值范围．21．（12分）若二次函数f（x）=x2+bx+c满足f（2）=f（﹣2），且函数的f（x）的一个根为1．（Ⅰ）求函数f（x）的解析式；（Ⅱ）对任意的x∈[，+∞），方程4mf（x）+f（x﹣1）=4﹣4m有解，求实数m的取值范围．22．（12分）定义在D上的函数f（x），如果满足：对任意x∈D，存在常数M≥0，都有|f（x）|≤M成立，则称f（x）是D上的有界函数，其中M称为函数f （x）的一个上界．已知函数f（x）=1+a（）x+（）x，若函数f（x）在[﹣2，1]上是以3为上界的有界函数，求实数a的取值范围．2016-2017学年江西省上饶市横峰中学高一（上）期中数学试卷参考答案与试题解析一、选择题：（本题包括12小题，共60分，每小题只有一个选项符合题意）1．（5分）设f（x）=，则f（f（﹣2））的值为（）A．3 B．6 C．9 D．12【解答】解：f（x）=，则f（f（﹣2））=f（4﹣1）=f（3）=3×3=9．故选：C．2．（5分）集合A={y|y=}，B={x|log2（x﹣2）≤1}，则A∩B（）A．[1，4]B．[0，4]C．[0，2]D．（2，4]【解答】解：集合A={y|y=}={y|y≥0}=[0，+∞），B={x|log2（x﹣2）≤1}={x|0＜x﹣2≤2}={x|2＜x≤4}=（2，4]；所以A∩B=（2，4]．故选：D．3．（5分）已知a＞0且a≠1，下列四组函数中表示相等函数的是（）A．与y=2log a x B．y=2x与C．与D．与y=x【解答】解：对于A，函数y=log a x2=2log a|x|，与y=2log a x的对应关系不同，不是同一函数；对于B，函数y=2x，与y=log a a2x=2x的定义域均为R，对应关系也相同，是同一函数；对于C，函数y=（x≤﹣2或x≥2），与y=•=（x≥2）的定义域不同，不是同一函数；对于D，函数y==|x|，与y=x的对应关系不同，不是同一函数．故选：B．4．（5分）下列函数中，是偶函数，且在区间（0，1）上为增函数的是（）A．y=|x|B．y=3﹣x C．y= D．y=﹣x2+4【解答】解：y=|x|是偶函数，并且在区间（0，1）上为增函数，正确；y=3﹣x不是偶函数，错误；y=是奇函数，不正确；y=﹣x2+4是偶函数，但是在区间（0，1）上为减函数，不正确；故选：A．5．（5分）若函数y=f（x）的定义域是[0，2]，则函数g（x）=的定义域是（）A．[0，1]B．[0，1） C．[0，1）∪（1，4]D．（0，1）【解答】解：因为f（x）的定义域为[0，2]，所以对g（x），0≤2x≤2且x≠1，故x∈[0，1），故选：B．6．（5分）已知a=log0.60.5，b=ln0.5，c=0.60.5．则（）A．a＞b＞c B．a＞c＞b C．c＞a＞b D．c＞b＞a【解答】解：log0.60.5＞1，ln0.5＜0，0＜0.60.5＜1，即a＞1，b＜0，0＜c＜1，故a＞c＞b，故选：B．7．（5分）已知f（x）在（﹣∞，0]上是单调递增的，且图象关于y轴对称，若f（x﹣2）＞f（2），则x的取值范围是（）A．（﹣∞，0）∪（4，+∞）B．（﹣∞，2）∪（4，+∞）C．（2，4）D．（0，4）【解答】解：∵f（x）在（﹣∞，0]上是单调递增的，且图象关于y轴对称，∴函数f（x）是偶函数，且函数f（x）在[0，+∞）上为减函数，则不等式f（x﹣2）＞f（2），等价为f（|x﹣2|）＞f（2），则|x﹣2|＜2，则﹣2＜x﹣2＜2，得0＜x＜4，故选：D．8．（5分）幂函数f（x）=（m2﹣4m+4）x在（0，+∞）为减函数，则m 的值为（）A．1或3 B．1 C．3 D．2【解答】解：∵为幂函数∴m2﹣4m+4=1，解得m=3或m=1．由当x∈（0，+∞）时为减函数，则m2﹣6m+8＜0，解得2＜m＜4．∴m=3，故选：C．9．（5分）已知函数f（x）=（x﹣a）（x﹣b）（其中a＞b），若f（x）的图象如图所示，则函数g（x）=a x+b的图象大致为（）A．B．C．D．【解答】解：由二次方程的解法易得（x﹣a）（x﹣b）=0的两根为a、b；根据函数零点与方程的根的关系，可得f（x）=（x﹣a）（x﹣b）的零点就是a、b，即函数图象与x轴交点的横坐标；观察f（x）=（x﹣a）（x﹣b）的图象，可得其与x轴的两个交点分别在区间（﹣∞，﹣1）与（0，1）上，又由a＞b，可得b＜﹣1，0＜a＜1；在函数g（x）=a x+b可得，由0＜a＜1可得其是减函数，又由b＜﹣1可得其与y轴交点的坐标在x轴的下方；分析选项可得A符合这两点，BCD均不满足；故选：A．10．（5分）已知定义在R上函数f（x）=对任意x1≠x2都有（x1﹣x2）[f（x1）﹣f（x2）]＜0，那么a的取值范围是（）A．（0，1） B．（0，）C．[，）D．[，1）【解答】解：对任意x1≠x2都有（x1﹣x2）[f（x1）﹣f（x2）]＜0，∴函数f（x）在R上为减函数，∵f（x）=，∴，解得≤a＜，故选：C．11．（5分）已知函数f（x）=，若关于x的方程f（x）=k有两个不等的实根，则实数k的取值范围是（）A．（0，+∞）B．（﹣∞，1）C．（1，+∞）D．（0，1]【解答】解：画出函数f（x）=的图象，和直线y=k，关于x的方程f（x）=k有两个不等的实根等价于f（x）的图象与直线有且只有两个交点．观察得出：（1）k＞1，或k＜0有且只有1个交点；（2）0＜k≤1有且只有2个交点．故实数k的取值范围是（0，1]．故选：D．12．（5分）设f（x）满足f（﹣x）=﹣f（x），且在[﹣1，1]上是增函数，且f（﹣1）=﹣1，若函数f（x）≤t2﹣2at+1对所有的x∈[﹣1，1]，当a∈[﹣1，1]时都成立，则t的取值范围是（）A．﹣≤t≤B．﹣2≤t≤2C．t≥或t≤﹣或t=0 D．t≥2或t≤﹣2或t=0【解答】解：若函数f（x）≤t2﹣2at+1对所有的x∈[﹣1，1]都成立，由已知易得f（x）的最大值是1，∴1≤t2﹣2at+1⇔2at﹣t2≤0，设g（a）=2at﹣t2（﹣1≤a≤1），欲使2at﹣t2≤0恒成立，则⇔t≥2或t=0或t≤﹣2．故选：D．二、非选择题：（本题包括4小题，共20分）13．（5分）函数y=f（x）图象与函数y=log a x图象关于直线y=x对称，则函数y=f （x﹣1）图象过定点（1，1）．【解答】解：∵函数y=f（x）图象与函数y=log a x图象关于直线y=x对称，∴y=f（x）=a x，∴y=f（x﹣1）=a x﹣1；则当x=1时，a0=1，即函数y=f（x﹣1）图象过定点（1，1）．故答案为（1，1）．14．（5分）函数f（x）=（x2﹣6x+5）的单调递减区间是（5，+∞）．【解答】解：有函数f（x）有意义得x2﹣6x+5＞0，解得x＜1或x＞5．令g（x）=x2﹣6x+5，则g（x）在（﹣∞，1）上单调递减，在（5，+∞）上单调递增，∴f（x）=log（x2﹣6x+5）在（﹣∞，1）上单调递增，在（5，+∞）上单调递减．故答案为（5，+∞）15．（5分）若函数y=x2﹣3x﹣4的定义域为[0，m]，值域为[﹣，﹣4]，则m 的取值范围是[，3] ．【解答】解：∵f（x）=x2﹣3x﹣4=（x﹣）2﹣，∴f（）=﹣，又f（0）=﹣4，故由二次函数图象可知：m的值最小为；最大为3．m的取值范围是：≤m≤3．故答案[，3]16．（5分）已知集合A={（x，y）|y=0.2|x|﹣1}，集合B={（x，y）|y=m}，若A ∩B≠∅，则实数m的取值范围是（﹣1，0] ．【解答】解：A={（x，y）|y=0.2|x|﹣1}，B={（x，y）|y=m}，画出函数y=0.2|x|﹣1和y=m的图象，如图示：，若A∩B≠∅，则（﹣1，0]，故答案为：（﹣1，0]．三、解答题：本大题共6小题，解答应写出文字说明，证明过程或演算步骤17．（10分）计算下列各式的值：（1）﹣（）0+（）﹣0.5+；（2）lg500+lg﹣lg64+50（lg2+lg5）2．【解答】解：（1）﹣（）0+（）﹣0.5+=+1﹣1++e﹣=+e．（2）lg500+lg﹣lg64+50（lg2+lg5）2=lg5+2+3lg2﹣lg5﹣3lg2+50（lg10）2=lg5+2+3lg2﹣lg5﹣3lg2+50=52．18．（12分）已知集合A={x|（x﹣a）[x﹣（a+3）]≤0}（a∈R），B={x|x2﹣4x ﹣5＞0}．（1 ）若A∩B=∅，求实数a的取值范围；（2 ）若A∪B=B，求实数a的取值范围．【解答】解：A={x|（x﹣a）[x﹣（a+3）]≤0}={x|a≤x≤a+3}，B={x|x2﹣4x﹣5＞0}={x|x＜﹣1或x＞5}，…（4分）（1）要使A∩B=∅，则需满足下列不等式组，解此不等式组得﹣1≤a≤2，则实数a的取值范围为[﹣1，2]…（8分）（2）要使A∪B=B，即A是B的子集，则需满足a+3＜﹣1或a＞5，解得a＞5或a＜﹣4，即a的取值范围是{a|a＞5或a＜﹣4}…（12分）19．（12分）已知定义在R上的奇函数f（x），当x＞0时，f（x）=﹣x2+2x （Ⅰ）求函数f（x）在R上的解析式；（Ⅱ）若函数f（x）在区间[﹣1，a﹣2]上单调递增，求实数a的取值范围．【解答】解：（Ⅰ）设x＜0，则﹣x＞0，f（﹣x）=﹣（﹣x）2+2（﹣x）=﹣x2﹣2x．又f（x）为奇函数，所以f（﹣x）=﹣f（x）且f（0）=0．于是x＜0时f（x）=x2+2x．所以f（x）=．（Ⅱ）作出函数f（x）=的图象如图：则由图象可知函数的单调递增区间为[﹣1，1]要使f（x）在[﹣1，a﹣2]上单调递增，（画出图象得2分）结合f（x）的图象知，所以1＜a≤3，故实数a的取值范围是（1，3]．20．（12分）已知定义在R上的函数f（x），对任意a，b∈R，都有f（a+b）=f （a）+f（b）﹣1，当x＞0时，f（x）＞1；且f（2）=3，（1）求f（0）及f（1）的值；（2）判断函数f（x）在R上的单调性，并给予证明；（3）若f（﹣kx2）+f（kx﹣2）＜2对任意的x∈R恒成立，求实数k的取值范围．【解答】解：（1）令a=b=0，由题意可知：f（0）=f（0）+f（0）﹣1，即f（0）=1，同理，令a=b=1，则有f（2）=f（1）+f（1）﹣1，又f（2）=3，所以f（1）=2；…（2分）（2）在R上任取x1、x2，设x1＞x2，则f（x1）=f（x1﹣x2）+f（x2）﹣1，所以f（x1）﹣f（x2）=f（x1﹣x2）﹣1，又当x＞0时，f（x）＞1且x1﹣x2＞0，所以f（x1﹣x2）＞1，所以f（x1）﹣f（x2）＞0，即f（x1）＞f（x2）故函数f（x）在R上为单调递增；…（6分）（3）因为f（﹣kx2）+f（kx﹣2）＜2对任意的x∈R恒成立，由题意可转化为kx2﹣kx+2＞0对任意的x∈R恒成立，…（7分）①当k=0时，得2＞0，符合题意；…（9分）②当k≠0时，则，解得0＜k＜8…（11分）故符合题意的实数k的取值范围为0≤k＜8…（12分）21．（12分）若二次函数f（x）=x2+bx+c满足f（2）=f（﹣2），且函数的f（x）的一个根为1．（Ⅰ）求函数f（x）的解析式；（Ⅱ）对任意的x∈[，+∞），方程4mf（x）+f（x﹣1）=4﹣4m有解，求实数m的取值范围．【解答】解：（Ⅰ）∵f（2）=f（﹣2）且f（1）=0，函数的f（x）的一个根为1，b+c=0，f（2）=f（﹣2）可得：4+2b+c=4﹣2b+c，∴b=0，c=﹣1，∴f（x）=x2﹣1．（5分）（Ⅱ）由题意知：4m2（x2﹣1）+（x﹣1）2﹣1+4m2﹣4≥0在上有解，整理得在上有解，令g（x）=，∵，∴当时，函数g（x）得最大值，所以．（12分）22．（12分）定义在D上的函数f（x），如果满足：对任意x∈D，存在常数M≥0，都有|f（x）|≤M成立，则称f（x）是D上的有界函数，其中M称为函数f （x）的一个上界．已知函数f（x）=1+a（）x+（）x，若函数f（x）在[﹣2，1]上是以3为上界的有界函数，求实数a的取值范围．【解答】解：由题意知，|f（x）|≤3在[﹣2，1]上恒成立．所以﹣3≤f（x）≤3，即．∴在[﹣2，1]上恒成立．∴…（4分）设2x=t ，，，由x∈[﹣2，1]得，…（6分）则h（t ）在上的最大值为，…（9分）p（t ）在上的最小值为．…（11分）所以实数a 的取值范围为．…（12分）赠送：初中数学几何模型举例【模型四】几何最值模型：图形特征：BAPl运用举例：1. △ABC中，AB=6，AC=8，BC=10，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为AP的中点，则MF的最小值为B2.如图，在边长为6的菱形ABCD中，∠BAD＝60°，E为AB的中点，F为AC上一动点，则EF+BF的最小值为_________。

横峰中学2016高一分班考试化学试卷可能用到的相对原子质量：H-1 C-12 N-14 O-16 Cl-35.5 Al-27 Fe-56 Cu-64Na-23 S-32第I卷（共40分）一．选择题（40分）：（本大题共16个小题，1---8每小题2分，9---16每小题3分．在每小题给出的四个选项中，只有一个选项符合题目要求）1．下列有关物质的分类正确的是（）A．纯净物：水银、氢氧化铁固体、冰水混合物B．碱性氧化物：Na2O、Na2O2、Al2O3 C．盐：纯碱、小苏打、烧碱D．电解质：CH3COOH、H2O、NH32．下列仪器常用于物质分离的是①漏斗②试管③蒸馏烧瓶④天平⑤分液漏斗⑥研钵A．①③④B．①②⑥C．①③⑤D．①③⑥3．N A表示阿伏加德罗常数，下列说法正确的是( )A．质量为16g的O2和O3的混合气体中所含的氧原子的个数为N AB．18 g NH4+含有质子数为10N AC．1 mol过氧化钠与足量水反应时，转移电子的数目为2N AD．0.1 mol•L﹣1的NaCl溶液中，Na+与Cl﹣的离子总数为0.2N A4．下列物质均有漂白作用，其漂白原理相同的是（）①过氧化钠②次氯酸③双氧水④活性炭⑤二氧化硫⑥臭氧．A．①②③⑤ B．只有①②③⑥ C．②③④⑤ D．只有①③⑤⑥5．在2H2S+SO2═3S↓+2H2O的反应中，当有8×6.02×1023个电子发生转移时，得到的氧化产物比还原产物多（）A．64 g B．32 g C．1.5mol D．3 mol6.下列各组中两物质相互反应时，若改变反应条件（温度、反应物用量比）化学反应并不改变的是（）A．Na2O2和H2O B．Na和O2 C．NaOH和CO2 D．NaOH和AlCl37．在溶液中能大量共存，加入OH－有沉淀析出，加入H+有气体放出的是（）A．Na+、Cu2+、Cl－、SO42－B．Na+、Ca2+、Cl－、HCO3－C．H+、Al3+、OH－、NO3－D．Fe3+、K+、SO42－、NO3－8．下列溶液与20mL 1mol•L﹣1 NaNO3溶液中NO3﹣物质的量浓度相等的是（）2Na 2NH 3 === 2NaNH 2 HCaO 2NH 4Cl === CaCl2 H 2O 3Mg(NH 2)2 === Mg 3N 2 4NH NH 4Cl NaNH 2 === NaCl 2NH 3（l ）Na 2NH3 === 2NaNH 2 H CaO 2NH 4Cl === CaCl 2 2NH 3 H 2O 3Mg(NH 2)2 === Mg 3N 2 4NH NH 4Cl NaNH 2 === NaCl 2NH 3（l ）Na 2NH 3 === 2NaNH 2 H 2CaO 2NH 4Cl === CaCl 2 2NH 3 H 2O 3Mg(NH 2)2 === Mg 3N 2 4NH 3NH 4Cl NaNH 2 === NaCl 2NH 3（l ）2Na 2NH 3 === 2NaNH 2 H 2CaO 2NH 4Cl === CaCl 2 2NH H 2O 3Mg(NH 2)2 === Mg 3N 2 4NH 3NH 4Cl NaNH 2 === NaCl 2NH 3（l ）A ．10mL 1mol•L ﹣1 Mg （NO 3）2溶液 B ．5mL 0.8mol•L ﹣1 Al （NO 3）3溶液C ．10mL 2mol•L ﹣1AgNO 3溶液D ．10mL 0.5mol•L ﹣1 Cu （NO 3）2溶液9．已知在热的碱性溶液中，NaClO 能发生如下反应：3NaClO ＝2NaCl ＋NaClO 3。

2016-2017学年江西省上饶市横峰中学高一（上）期中化学试卷一、选择题:（本题包括16小题，共48分，每小题只有一个选项符合题意）1．滨海新区8.12爆炸事故给我们敲响了安全的警钟，对危险化学品要在包装上有警示标志．下列化学药品与其危险化学品图形标志不一致的一组是（）A．硫磺B．高锰酸钾C．氢气D．乙醇2．做化学实验时，必须十分重视实验安全．下列有关实验操作不符合上述要求的是(）A．在气体发生装置上点燃氢气等气体时，必须先检验气体的纯度B．加热灼烧后的坩锅放置在实验桌上冷却至室温C．若不小心打翻酒精灯使酒精着火时,应用湿抹布盖灭D．蒸馏操作过程中，若发现忘加沸石，应立即停止加热，待烧瓶冷却后再加入沸石3．下列有关物质的分类正确的是()A．混合物：空气、矿泉水、水银B．酸性氧化物:、CO2、SO2、COC．盐：醋酸钠、氯化铵、纯碱 D．弱电解质:CH3COOH、H2O、NH34．下列叙述正确的是（)A．1 mol H2O的质量为18g/molB．3。

01×1023个SO2分子的质量为32gC．CH4的摩尔质量为16gD．标准状况下，1 mol任何物质的体积均为22。

4L5．用N A表示阿伏加德罗常数的值,下列叙述正确的是(）A．标准状况下含有N A个氦原子的氦气的体积约为11。

2LB．1 L 0。

1 mol/LNaHSO4溶液中含有0.1N A个HSO4﹣C．标准状况下,22。

4 L CCl4所含的分子数约为N AD．CO和N2组成的42g混合气体中原子的个数为3N A6．下列溶液中Na+与50mL 3mol•L﹣1 NaCl溶液中Na+物质的量浓度相等的是() A．150 mL 1 mol•L﹣1Na3PO4溶液B．75 mL 2 mol•L﹣1NaNO3溶液C．75 mL 3 mol•L﹣1Na2SO4溶液D．150 mL 2mol•L﹣1NaCl溶液7．下列离子方程式，正确的是(）A．铜与盐酸反应：Cu+2H+═Cu2++H2↑B．氧化铁与稀盐酸反应：Fe2O3+6H+═2Fe3++3H2OC．锌与硝酸银溶液反应:Zn+Ag+═Zn2++AgD．在硫酸溶液中加入氢氧化钡溶液:Ba2++OH﹣+H++SO42﹣═BaSO4↓+H2O8．在强酸性溶液中能大量共存的无色透明离子组是（)A．Mg2+Na+Cl﹣SO42﹣B．K+Na+CO32﹣NO3﹣C．K+Na+ Cl﹣Cu2+ D．Na+Ba2+OH﹣SO42﹣9．下列反应是氧化还原反应，但不属于四大基本反应类型的是（）A．4NH3+5O2═4NO+6H2O B．4Fe（OH）2+O2+2H2O═4Fe（OH)3C．2NaHCO3═Na2CO3+H2O+CO2D．Cl2+2NaBr═2NaCl+Br210．下列变化需要加入氧化剂才能实现的是(）A．H2O2→O2B．HCl→Cl2C．H2SO4→BaSO4D．CuO→Cu11．在下列化学方程式中，能够用离子方程式H++OH﹣=H2O表示的是（)A．醋酸溶液与氢氧化钠溶液反应B．盐酸与氨水反应C．硫酸氢钠溶液与氢氧化钾溶液反应D．氢氧化铁与硫酸溶液反应12．已知常温下,在溶液中发生如下反应：①16H++10Z﹣+2XO4﹣=2X2++5Z2+8H2O；②2A2++B2=2A3++2B﹣；③2B﹣+Z2=B2+2Z﹣由此推断下列说法错误的是（）A．反应Z2+2A2+=2A3++2Z﹣可以进行B．Z元素在①反应中被氧化，在③反应中被还原C．还原性由强到弱的顺序是Z﹣，B﹣，A2+,X2+D．氧化性由强到弱的顺序是XO4﹣，Z2，B2，A3+13．下列描述正确的是（）A．溶液是电中性的，胶体是带电的B．CO2的水溶液能导电，所以CO2为电解质C．可使用丁达尔效应来区分FeCl3溶液和Fe（OH）3胶体D．1 mol 任何物质均含有约6。

2016—2017学年江西省横峰中学高二上学期期中考试文科数学一、选择题：共12题1．若,a＞b，则下列不等式成立的是A。

B。

C。

D。

【答案】C【解析】本题只提供了“a，b,c∈R，a＞b”这个条件，而不等式的基本性质中，几乎都有类似的前提条件，但结论会根据不同的要求有所不同，因而这需要根据本题的四个选项来进行判断.选项A,还需有ab＞0这个前提条件;选项B，当a，b都为负数时不成立.或一正一负时可能不成立,如2＞－3,但22＞（－3)2不正确；对于选项C，，由a＞b就可知，故正确；选项D，当c＝0时不正确.【备注】对于考查不等式的基本性质的选择题，解答时，一是利用不等式的相关性质，其中，特别要注意不等号变号的影响因素，如数乘、取倒数、开方、平方等;二是对所含字母取特殊值，结合排除法去选正确的选项，这种方法一般要注意选取的值应具有某个方面的代表性,如选取0、正数、负数等.2．10名工人某天生产同一零件，生产的件数是15，17，14，10，15，17，17，16，14，12。

设其平均数为a，中位数为b,众数为c,则有A.a>b>c B。

b>c〉a C。

c〉a>b D.c〉b〉a【答案】D【解析】对于一组数据，通常要求的是这组数据的众数，中位数，平均数，它们分别表示一组数据的特征，这样的问题可以出现在选择题或填空题．∵生产的件数是15，17，14，10，15，17，17，16,14，12总和为147，∴平均数,样本数据17出现次数最多,为众数，即；从小到大排列中间二位的平均数,即中位数．∵，．故选D。

3．数据5，7，7,8,10，11的标准差是A.8B.4C.2D.1【答案】C【解析】本题主要考查数据的标准差，根据标准差的公式进行求解即可。

∵5，7，7,8，10，11的平均数是∴这组数据的方差是∴这组数据的标准差是故选C。

4．已知，函数的最小值是A.5 B。

4 C。

8 D.6【答案】B【解析】本题主要考查利用基本不等式求最值。