杆件应力计算公式

结构力学常用公式
1.应力公式：σ=F/A，其中 F 为作用力，A 为作用面积，σ为应力。

2. 应变公式：ε = ΔL/L0，其中ΔL 为变形量，L0 为原始长度，ε为应变。

3. 弹性模量公式：E = σ/ε，其中 E 为弹性模量。

4. 餘弦定理：c = a + b - 2abcosC，其中 a，b 为两边的长度，
C 为两边之间的夹角，c 为斜边的长度。

5. 正弦定理：a/sinA = b/sinB = c/sinC，其中 a，b，c 为三角形三条边的长度，A，B，C 为三角形对应的内角。

6. 面积公式：A = 1/2bh，其中 b 为底边的长度，h 为高度。

7. 矩形截面抵消矩阵算式：I = bh/12，其中 I 为矩形截面的抵消矩阵，b 为宽度，h 为高度。

8. 圆形截面抵消矩阵算式：I = πr/4，其中 I 为圆形截面的抵消矩阵，r 为半径。

9. 计算杆件最大承受力公式：Fmax = σmaxA，其中 Fmax 为杆件最大承受力，σmax 为材料的最大允许应力，A 为杆件横截面积。

10. 悬索线的张力公式：T = (Wl)/(8d)，其中 T 为悬索线的张力，W 为悬挂物的重量，l 为悬挂物的长度，d 为悬索线的跨度。

- 1 -。

杆件正应力怎么求计算公式杆件正应力的计算公式。

在工程力学中，杆件正应力是指在杆件内部由外部加载引起的正向拉伸或压缩应力。

正应力的计算是工程设计中非常重要的一部分，它可以帮助工程师确定杆件是否能够承受外部加载，并且可以帮助工程师选择合适的材料和尺寸来设计结构。

杆件正应力的计算公式可以通过简单的力学原理推导得出。

在这篇文章中，我们将介绍杆件正应力的计算公式，并且讨论一些实际应用中的例子。

杆件正应力的计算公式可以表示为：σ = P / A。

其中，σ表示杆件的正应力，P 表示施加在杆件上的外部力，A 表示杆件的横截面积。

这个公式的推导可以通过简单的力学原理来进行。

当一个外部力 P 作用在杆件上时，杆件内部会产生一个与外部力方向相反的内部应力。

根据牛顿第三定律，这个内部应力的大小与外部力的大小相等，方向相反。

而杆件的横截面积 A 则可以用来表示内部应力的分布情况。

因此，杆件的正应力可以表示为外部力 P 与横截面积 A 的比值。

在实际应用中，杆件正应力的计算可以通过这个简单的公式来进行。

例如，当一个钢杆承受一个拉力时，我们可以通过测量钢杆的横截面积和外部拉力来计算钢杆的正应力。

这个计算可以帮助工程师确定钢杆是否能够承受这个拉力，并且可以帮助工程师选择合适的钢材来设计结构。

除了上面提到的简单拉力的情况，杆件正应力的计算公式也可以应用在其他复杂的情况中。

例如，在梁的设计中，梁的横截面积不是均匀的，因此我们可以通过积分的方法来计算梁的正应力分布。

这个计算可以帮助工程师确定梁在不同位置的正应力大小，并且可以帮助工程师选择合适的梁的尺寸和材料来设计结构。

除了简单的拉力和梁的设计，杆件正应力的计算公式也可以应用在其他工程结构的设计中。

例如，在桥梁的设计中，我们可以通过计算桥梁的正应力来确定桥梁的承载能力，并且可以帮助工程师选择合适的桥梁的尺寸和材料来设计结构。

总之，杆件正应力的计算公式是工程设计中非常重要的一部分。

通过这个简单的公式，工程师可以确定杆件是否能够承受外部加载，并且可以帮助工程师选择合适的材料和尺寸来设计结构。

杆件的轴向应变和轴向力计算杆件是工程中常见的构件之一，广泛应用于建筑、桥梁、机械等领域。

在设计和分析杆件时，了解轴向应变和轴向力的计算方法是非常重要的。

一、轴向应变的定义和计算方法轴向应变是指杆件在受到轴向力作用时，单位长度的变形量。

轴向应变可以用公式表示为：ε = ΔL / L其中，ε表示轴向应变，ΔL表示杆件在受到轴向力作用后的长度变化量，L表示杆件的原始长度。

轴向应变的计算方法主要有以下几种：1. 直接测量法：通过使用应变计等测量仪器，直接测量杆件在受力后的长度变化量，然后根据上述公式计算轴向应变。

2. 应变计法：在杆件上粘贴应变计，应变计的电阻值会随着杆件受力而发生变化，通过测量电阻值的变化，可以计算出轴向应变。

3. 数值模拟法：通过有限元分析等数值方法，对杆件的受力情况进行模拟计算，从而得到轴向应变的数值结果。

二、轴向力的定义和计算方法轴向力是指作用在杆件上的沿着杆件轴线方向的力。

轴向力可以用公式表示为：N = A * σ其中，N表示轴向力，A表示杆件的横截面积，σ表示轴向应力。

轴向力的计算方法主要有以下几种：1. 直接测量法：通过使用力传感器等测量仪器，直接测量作用在杆件上的轴向力。

2. 应力计算法：根据杆件受力情况和材料的力学性能参数，计算轴向应力，然后通过上述公式计算轴向力。

3. 数值模拟法：通过有限元分析等数值方法，对杆件的受力情况进行模拟计算，从而得到轴向力的数值结果。

三、轴向应变和轴向力的关系轴向应变和轴向力之间存在一定的关系。

根据胡克定律，轴向应变和轴向力之间的关系可以表示为：σ = E * ε其中，σ表示轴向应力，E表示杆件的弹性模量，ε表示轴向应变。

根据上述公式，可以通过已知轴向应变或轴向力，计算出轴向应力。

同时，也可以通过已知轴向应力和轴向应变，计算出杆件的弹性模量。

四、轴向应变和轴向力的应用轴向应变和轴向力的计算在工程设计和分析中有着广泛的应用。

通过对轴向应变和轴向力的计算，可以评估杆件的受力状态和变形情况，从而确定杆件的安全性和可靠性。

扭转杆件的应力计算公式在工程学中，扭转杆件是一种常见的结构元件，它们通常用于承受扭转力或者转矩。

在设计和分析扭转杆件时，计算其应力是非常重要的。

本文将介绍扭转杆件的应力计算公式以及相关的理论知识。

扭转杆件的应力计算公式可以通过以下步骤推导得到。

首先，我们需要了解扭转杆件的基本几何形状和材料性质。

扭转杆件通常是圆柱形状的，其直径为d，长度为L。

材料的弹性模量为E，剪切模量为G。

在扭转杆件上施加一个扭矩T，我们可以得到以下的应力计算公式：τ = Tr/J。

其中，τ是扭转杆件上的剪切应力，T是施加在扭转杆件上的扭矩，r是扭转杆件上某一点到中心轴的距离，J是扭转杆件的极惯性矩。

极惯性矩J可以通过以下公式计算得到：J = πd^4/32。

通过将极惯性矩J代入到剪切应力的公式中，我们可以得到扭转杆件上的最大剪切应力：τ_max = Tc/J。

其中，c是扭转杆件的半径。

最大剪切应力发生在扭转杆件的表面，其值可以用来判断扭转杆件的强度和稳定性。

在实际工程中，我们通常需要计算扭转杆件上的最大剪切应力。

为了更好地理解扭转杆件的应力分布情况，我们可以绘制出扭转杆件上的剪切应力分布图。

根据应力计算公式，我们可以得到扭转杆件上不同点的剪切应力值，然后将这些值绘制成图表，以便工程师们更好地分析和理解扭转杆件的应力分布情况。

除了计算扭转杆件上的最大剪切应力外，我们还需要考虑扭转杆件的变形情况。

在扭转杆件上施加扭矩时，会产生一定的变形，这种变形可以通过以下公式计算得到：θ = TL/(GJ)。

其中，θ是扭转杆件上某一点的角度变化，L是扭转杆件的长度，G是材料的剪切模量。

通过计算扭转杆件上不同点的角度变化，我们可以得到扭转杆件的整体变形情况。

在实际工程中，我们还需要考虑扭转杆件的疲劳寿命。

由于扭转杆件通常需要长时间承受扭转力，因此其疲劳寿命是非常重要的。

我们可以通过应力分析和疲劳试验来评估扭转杆件的疲劳寿命，以确保其在使用过程中不会发生断裂或者变形。

理论力学中的杆件受力分析与扭矩计算理论力学是研究物体运动和受力的经典物理学分支。

在理论力学中，对于杆件受力分析和扭矩计算有着重要的研究和应用。

本文将从理论力学的角度，探讨杆件受力分析以及扭矩的计算方法。

一、杆件受力分析在理论力学中，杆件是常见的力学结构，主要用于支撑和传递力的作用。

杆件受力分析是研究杆件内部受力情况的过程，其中包括了杆件的静力学平衡和杆件的应力分析。

下面将从这两个方面进行介绍。

1.1 杆件的静力学平衡在进行杆件受力分析时，首先需要保证杆件的静力学平衡。

静力学平衡是指杆件内外的力和扭矩之间的平衡关系。

对于一个静止的杆件而言，其受力平衡方程可以表示为：ΣF_x=0 (1)ΣF_y=0 (2)ΣM=0 (3)其中，ΣF_x和ΣF_y分别表示杆件上的水平力和垂直力之和，ΣM表示杆件上的扭矩之和。

通过这些平衡方程，可以求解得到杆件上各个点的受力情况。

1.2 杆件的应力分析在静力学平衡的基础上，需要对杆件的应力进行进一步的分析。

应力是指单位面积上的力的大小，可分为正应力和剪切应力两种类型。

在杆件受力分析中，常常关注的是杆件上的正应力情况。

根据杆件受力分析的结果，可以利用材料力学的知识，计算出杆件上各个点的正应力大小。

常用的应力计算公式包括弯曲应力、拉压应力和剪切应力等。

二、扭矩的计算方法扭矩是指力对物体产生旋转效应的力矩，是杆件受力分析中重要的参数。

在理论力学中，扭矩的计算常常以杆件的转动为基础。

2.1 扭矩的定义杆件的扭矩可以通过以下公式计算：M = F × d (4)其中，M表示扭矩大小，F表示作用在物体上的力的大小，d表示力作用点到转轴的距离。

扭矩的单位通常为牛顿·米（N·m）或者千克·米（kg·m）。

2.2 扭矩的计算方法杆件的扭矩计算涉及到受力分析和力矩的计算。

在进行扭矩计算时，常需要考虑以下几个方面：（1）确定转轴位置：正确选择与杆件转动有关的转轴位置，转轴的选择将直接影响到扭矩的计算结果。

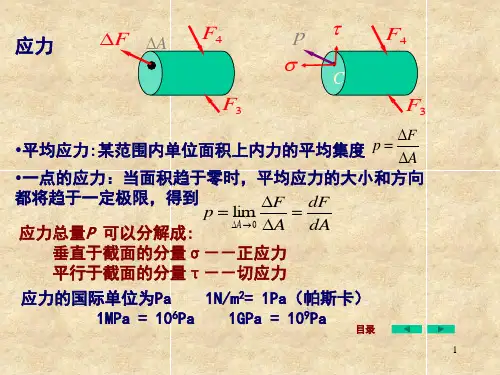
杆件横截面正应力计算公式在工程领域中，杆件的设计和计算是非常重要的。

杆件在受力作用下会产生正应力，而正应力的计算对于杆件的安全性和稳定性具有重要意义。

本文将介绍杆件横截面正应力的计算公式及其应用。

杆件横截面正应力计算公式如下：σ = P/A。

其中，σ为杆件横截面上的正应力，P为作用在杆件上的力，A为杆件的横截面积。

在实际工程中，杆件通常会受到拉伸、压缩、弯曲等不同形式的受力。

对于不同形式的受力，杆件横截面正应力的计算公式也会有所不同。

首先，我们来看一下杆件受拉伸力作用下的正应力计算。

当杆件受到拉伸力P 作用时，横截面上的正应力可以通过上述公式计算得到。

在这种情况下，横截面上的正应力与拉伸力P成正比，横截面积A越大，正应力σ越小，杆件的承载能力也就越大。

接下来，我们来看一下杆件受压缩力作用下的正应力计算。

当杆件受到压缩力P作用时，横截面上的正应力同样可以通过上述公式计算得到。

在这种情况下，横截面上的正应力也与压缩力P成正比，横截面积A越大，正应力σ越小，杆件的承载能力也就越大。

此外，杆件在受力作用下还会产生弯曲。

在弯曲情况下，杆件横截面上的正应力计算公式为：σ = Mc/I。

其中，σ为杆件横截面上的正应力，M为弯矩，c为横截面上的某一点到中性轴的距离，I为横截面的惯性矩。

在弯曲情况下，横截面上的正应力与弯矩M成正比，c越大，正应力σ越小，杆件的承载能力也就越大。

而横截面的惯性矩I则反映了杆件抵抗弯曲变形的能力，I越大，杆件的抗弯能力越强。

综上所述，杆件横截面正应力的计算公式为σ = P/A，对于不同形式的受力，计算公式也会有所不同。

在实际工程中，我们需要根据杆件受力情况选择合适的计算公式，并结合材料的力学性能参数进行计算，以保证杆件的安全性和稳定性。

同时，合理设计杆件的横截面形状和尺寸，也可以有效地提高杆件的承载能力和使用寿命。

希望本文对杆件横截面正应力的计算有所帮助，谢谢阅读！。

截面正应力计算公式
1. 基本概念。

- 对于轴向拉压杆件，其横截面上的正应力计算公式为σ=(F_N)/(A)。

其中σ表示正应力，F_N为轴力（拉力为正，压力为负），A为横截面面积。

- 在计算轴力F_N时，通常采用截面法。

即假想地用一截面将杆件截开，研究其中一部分的受力平衡，从而确定轴力的大小和方向。

2. 梁弯曲时的正应力。

- 对于纯弯曲梁（梁的横截面上只有弯矩而无剪力的情况），其正应力计算公式为σ=(My)/(I_z)。

- 这里M为横截面上的弯矩，y为所求应力点到中性轴的距离，I_z为横截面对中性轴z的惯性矩。

- 对于横力弯曲（梁的横截面上既有弯矩又有剪力的情况），当梁的跨度l与横截面高度h之比l/h>5时，纯弯曲正应力公式σ=(My)/(I_z)仍可近似使用。

3. 组合变形下的正应力。

- 当杆件发生组合变形（如拉压与弯曲的组合、扭转与弯曲的组合等）时，可分别计算每种基本变形产生的正应力，然后根据叠加原理求出组合变形下的正应力。

- 例如对于拉压与弯曲组合变形的杆件，横截面上某点的正应力
σ=σ_N+σ_M，其中σ_N = (F_N)/(A)（拉压正应力），σ_M=(My)/(I_z)（弯曲正应力）。

应变和应力的计算公式嘿，咱今儿来聊聊应变和应力的计算公式。

先来说说啥是应变和应力。

这俩家伙在物理学和工程学里可重要着呢！应变啊，简单说就是物体在受到外力作用时发生的形状变化程度。

比如说，你拉一根橡皮筋，它被拉长了，这拉长的程度跟原来长度的比值就是应变。

应力呢，则是物体内部为了抵抗外力产生的内力分布情况。

那应变的计算公式是啥呢？应变通常用ε 表示。

对于线应变，如果一个杆件原来的长度是 L₀，受力后长度变成了 L，那线应变ε 就等于（L - L₀）/ L₀。

这就好比一根铅笔，你用力掰它，它变长或者变短的那部分和原来长度的比例就是线应变。

再讲讲应力。

应力一般用σ 表示。

假如一个杆件受到一个拉力 F，横截面积是 A，那正应力σ 就等于 F / A 。

就像拔河的时候，绳子内部承受的力和绳子横截面积的比值就是应力。

我给您说个我曾经遇到的事儿。

有一回，我在工厂里看到师傅们在检测一批金属材料。

他们拿着各种仪器测量，嘴里还念叨着应变和应力的数值。

我好奇地凑过去，师傅看我一脸懵，就拿起一块材料给我比划。

他说：“你看啊，这材料被拉伸的时候，长度变了，咱们就得用应变公式算算变了多少。

然后根据受力大小和面积，用应力公式看看材料能不能承受得住。

”我当时似懂非懂地点点头，心里琢磨着这可真不简单。

回到这计算公式，应变和应力在实际生活中的应用那可太广泛了。

比如说造桥，工程师得精确计算桥梁在各种车辆通行时的应变和应力，确保桥不会因为受力过大而垮掉。

还有制造飞机的零部件，那要求更是严格，一点点的误差都可能导致严重后果。

在材料科学研究中，应变和应力的计算也是关键。

通过对不同材料进行实验，得到应变和应力的数据，就能判断材料的性能好坏，找到更适合的材料来满足各种需求。

总之，应变和应力的计算公式虽然看起来有点复杂，但搞清楚了它们，对于解决很多实际问题那可是大有用处。

咱可不能小瞧了这几个公式，它们背后可是有着大大的学问和实际价值呢！。

中长杆件临界应力的计算公式应采用
在中长杆件的设计中，计算临界应力是非常重要的一环。

然而，不同的公式会得出不同的结果，因此需要选择合适的计算公式。

一般来说，中长杆件的临界应力计算公式可以采用以下几种：
1. 欧拉公式：适合于较长的杆件，且杆件端部固定或受到压力作用。

公式为：
Pcr = πEI / L
其中，Pcr为临界压力；E为弹性模量；I为截面转动惯量；L为杆件长度。

2. 弯曲应力公式：适用于长度较短的杆件，且杆件为悬臂式结构。

公式为：
Pcr = 4Fcr / πD
其中，Fcr为杆件的弯曲破坏载荷；D为杆件直径。

3. 临界剪切应力公式：适用于直径较小的杆件。

公式为：
Pcr = 4τcr / πD
其中，τcr为杆件的临界剪切应力。

综合考虑杆件的长度、形状和受力情况，选择合适的计算公式可以更准确地计算出中长杆件的临界应力，从而为设计提供重要的参考依据。

- 1 -。

应力力矩计算1. 应力力矩基础概念1. 应力力矩基础概念：应力力矩是指物体在受到外力作用时产生的力矩，它可以用来衡量物体的受力状态。

应力力矩的大小取决于外力的大小、方向和作用点的位置，以及物体的形状和尺寸。

应力力矩可以表示为物体受到的外力的合力乘以作用点到外力的距离，即F*d，其中F为外力的大小，d为作用点到外力的距离。

2. 应力力矩计算公式应力力矩计算公式：1. 圆柱体：τ = Fr2. 圆筒体：τ = Fd/23. 圆柱面：τ = Fd/44. 圆环：τ = Fd/25. 圆锥：τ = Fd/46. 圆柱锥：τ = Fd/27. 圆柱柱面：τ = Fd/48. 圆柱柱锥：τ = Fd/29. 梯形：τ = Fd/210. 平行四边形：τ = Fd/23. 应力力矩计算实例3. 应力力矩计算实例计算一个简单的应力力矩实例，假设一个杆件，长度为L，上端受到一个力F，下端受到一个力矩M。

计算这个杆件上的应力及应力力矩：首先，计算杆件上的应力：应力=F/A其中，A为杆件的断面积。

接下来，计算杆件上的应力力矩：应力力矩=M/I其中，I为杆件的惯性矩。

最后，计算杆件上的应力及应力力矩：应力=F/A应力力矩=M/I4. 应力力矩计算应用应力力矩计算可以应用于多种工程领域，如机械制造、航空航天、汽车制造等。

它可以用来计算机械结构的应力分布，以及机械零件的应力和变形状态。

此外，应力力矩计算还可以用来分析汽车车身结构、航空航天结构以及其他重型机械结构的应力分布。

应力力矩计算可以用来评估构件的疲劳寿命，以及检测构件的变形特性。

它还可以用来优化机械结构的设计，以满足特定的应力要求。

此外，应力力矩计算还可以用于确定某些零件的最佳尺寸，以满足特定的应力要求。

5. 应力力矩计算注意事项5. 应力力矩计算注意事项1. 需要确定应力力矩计算的物体材料及其尺寸；2. 需要确定应力力矩计算的载荷类型及其大小；3. 需要确定应力力矩计算的多自由度系统；4. 需要确定应力力矩计算的接触条件；5. 需要确定应力力矩计算的结构模型；6. 需要确定应力力矩计算的约束条件；7. 需要确定应力力矩计算的计算方法；8. 需要确定应力力矩计算的计算精度；9. 需要确定应力力矩计算的结果表示形式；10. 需要确定应力力矩计算的安全系数；。