工程力学(杆件弯曲受力分析计算)
- 格式:docx
- 大小:86.95 KB
- 文档页数:5




弯矩计算公式有几种方法在工程力学中,弯矩是一个重要的概念,用来描述在杆件或梁上受到的弯曲力。
弯矩的计算是工程设计中的重要一环,因此有多种方法可以用来计算弯矩。
本文将介绍几种常见的弯矩计算方法,包括静力学方法、弯曲理论方法和有限元分析方法。
静力学方法。
静力学方法是最基本的弯矩计算方法之一,它基于牛顿第二定律和力的平衡原理。
在静力学方法中,首先需要确定受力杆件的受力情况,然后利用受力平衡方程来计算弯矩。
对于简单的静力学问题,可以直接利用几何形状和力的大小来计算弯矩,但对于复杂的结构或受力情况,可能需要使用更复杂的方法来计算弯矩。
弯曲理论方法。
弯曲理论方法是一种基于材料力学和结构力学的弯矩计算方法。
在这种方法中,首先需要确定受力杆件的几何形状和材料特性,然后利用弯曲理论来计算弯矩。
弯曲理论方法可以分为弹性理论和塑性理论两种,分别适用于弯矩小于材料屈服强度和大于材料屈服强度的情况。
弯曲理论方法可以提供比静力学方法更精确的弯矩计算结果,因此在工程设计中得到了广泛的应用。
有限元分析方法。
有限元分析方法是一种基于数值计算的弯矩计算方法。
在这种方法中,首先需要将受力杆件的几何形状和材料特性建模成有限元网格,然后利用数值计算方法来求解受力杆件的弯矩。
有限元分析方法可以对复杂的受力情况进行精确的计算,并且可以考虑材料的非线性和结构的非均匀性。
因此,在工程设计中,有限元分析方法得到了广泛的应用。
综上所述,弯矩的计算可以通过静力学方法、弯曲理论方法和有限元分析方法来进行。
每种方法都有其适用的范围和优缺点,工程设计人员需要根据具体的情况来选择合适的方法来计算弯矩。
在实际工程中,通常会结合多种方法来进行弯矩计算,以确保计算结果的准确性和可靠性。
希望本文可以帮助读者更好地理解弯矩的计算方法,为工程设计提供参考。



屈曲分析屈曲分析是一种在工程力学中常见的分析方法,用于研究杆件在受力作用下的屈曲性能。
屈曲指的是杆件在受到压力作用时,由于材料的强度不足或几何形状的不合理,导致杆件发生弯曲或破坏的现象。
屈曲分析的目的是确定杆件的屈曲载荷和屈曲形态,以保证结构的安全可靠性。
屈曲分析主要涉及材料力学、结构力学和数值计算等方面的知识。
首先,我们需要了解材料的力学性能,包括材料的弹性模量、屈服强度和断裂韧性等。
这些参数将决定杆件是否具备抵抗屈曲的能力。
其次,结构力学的知识是进行屈曲分析的基础。
我们需要掌握静力学的基本原理,了解杆件在受力作用下的受力分布和相应的应力状态。
最后,数值计算方法可以帮助我们通过计算机模拟杆件的受力情况,得出屈曲载荷和屈曲形态。
在进行屈曲分析时,我们可以采用不同的理论模型,例如欧拉理论、托列密理论和von Mises理论等。
欧拉理论是最常用的屈曲分析方法之一,适用于长、细杆件的屈曲分析。
托列密理论则适用于短、粗杆件的屈曲分析。
von Mises理论是一种较为通用的屈曲分析方法,考虑了材料的屈服特性,适用于多种类型的杆件。
在进行屈曲分析时,我们需要首先确定杆件的几何形状和边界条件。
然后,在已知杆件的几何参数、材料参数和加载条件的情况下,可以利用力学理论和数值计算方法求解杆件的屈曲载荷和屈曲形态。
在求解过程中,需要进行数值模型的建立、边界条件的施加和求解方法的选择。
通过合理的假设和较为准确的计算,可以得到较为可靠的屈曲分析结果。
屈曲分析在工程设计中具有重要的意义。
通过屈曲分析,我们可以评估杆件的屈曲性能,确定结构的安全使用范围。
在设计过程中,我们可以调整材料的选择、几何形状的设计和支撑结构的设置等,以提高结构的屈曲承载能力。
此外,屈曲分析还可以为结构优化设计提供参考,以实现结构的轻量化和高效化。
总之,屈曲分析是研究杆件受力情况的重要方法之一。
通过屈曲分析,我们可以了解杆件的屈曲载荷和屈曲形态,为结构的设计和使用提供参考。

工程力学中的杆件力学分析工程力学是工科中的一门重要学科,主要研究固体和结构的力学性能和力学行为。
其中,杆件力学是工程力学中的重要组成部分之一。
杆件力学主要研究杆件的受力和变形,对于工程结构的设计和分析具有重要意义。
本文将从杆件力学的基本原理、力学分析方法和应用案例三个方面,对工程力学中的杆件力学进行深入探讨。
一、杆件力学的基本原理在工程力学中,杆件是指长条形构件,具有一定的刚度和承载能力。
杆件力学的基本原理包括静力学平衡和杆件内力平衡两个方面。
静力学平衡是指杆件受力的平衡条件。
根据力的平衡条件,杆件受力的合力为零,同时受力矩也为零。
通过静力学平衡的原理,可以分析杆件受力的大小和方向。
杆件内力平衡是指杆件内部各截面的内力保持平衡。
在杆件上任意取一截面,根据内力平衡条件,杆件的截面上受力的合力为零,同时受力矩也为零。
通过杆件内力平衡的原理,可以分析杆件不同截面上的内力分布情况。
二、杆件力学的力学分析方法杆件力学的力学分析方法主要包括静力学分析和变形分析两个方面。
静力学分析是指通过力的平衡条件,分析杆件受力的大小、方向和作用点位置等。
通过应用牛顿第二定律和力的平衡条件,可以得到杆件受力的解析表达式。
同时,结合几何关系和几何约束条件,可以进一步求解杆件受力的具体数值。
变形分析是指通过应力和应变关系,分析杆件在受力作用下的变形情况。
通过应用胡克定律和杨氏模量等力学性质,可以得到杆件的应变表达式。
同时,结合几何关系和几何约束条件,可以进一步求解杆件的位移和变形。
三、杆件力学的应用案例杆件力学在实际工程中具有广泛的应用价值。
以下将介绍两个与杆件力学相关的应用案例。
首先是杆件的承载能力分析。
在工程设计中,需要对杆件的承载能力进行评估和验证。
通过应用杆件力学的原理和方法,可以计算杆件的受力情况,并判断杆件是否满足设计和使用要求。
其次是杆件的优化设计。
在工程实践中,经常需要对杆件进行优化设计,以提高结构的性能和经济性。

工程力学中的杆件受力分析在结构设计中的应用工程力学是工程学科中的基础课程之一,它研究物体的受力与变形规律,为结构设计和工程施工提供理论基础。
在工程力学中,杆件受力分析是非常重要的内容之一。
本文将探讨杆件受力分析在结构设计中的应用。
一、杆件的概念和分类在工程力学中,杆件指的是具有一定长度的线状物体,其截面可以看作是无界面积的。
根据受力特点和结构用途,杆件可以分为受拉杆、受压杆、受弯杆和受扭杆等。
受力分析是研究杆件内部受力状态和变形规律的过程。
通过分析杆件的受力分布和受力大小,可以确定杆件在结构设计中的应用。
二、杆件受力分析的基本原理杆件受力分析的基本原理是力的平衡原理和杆件的几何约束条件。
根据力的平衡原理,杆件上各点的受力合力为零,即所有受力的矢量和为零。
根据杆件的几何约束条件,杆件上各点的位移和变形受到限制,从而确定杆件的约束方程。
通过解析力学的方法,可以得到杆件内部受力的大小和分布情况。
常用的方法有静力学方法和力矩平衡方法。
静力学方法适用于求解简单杆件的受力情况,力矩平衡方法则适用于求解复杂杆件的受力情况。
三、杆件受力分析在结构设计中的应用1. 强度计算结构设计中,杆件的强度计算是非常重要的一环。
通过杆件受力分析,可以确定杆件所受的最大受力和受力位置,从而计算杆件的强度。
不同材料和不同结构形式的杆件有不同的强度计算方法,但都离不开杆件受力分析的基本原理。
2. 结构稳定性分析结构设计中,结构的稳定性是必须考虑的因素之一。
杆件受力分析可以通过计算杆件的临界载荷和屈曲形态,评估结构的稳定性。
通过合理选择材料和截面形状,使得杆件在受力情况下保持稳定,确保结构的可靠性和安全性。
3. 结构刚度分析结构设计中,结构的刚度是影响结构整体性能的重要因素。
杆件受力分析可以通过计算杆件的刚度系数,评估结构的整体刚度。
通过合理设计杆件的长度、截面形状和材料性能,可以提高结构的刚度,提高结构的整体性能。
4. 构件的优化设计结构设计中,优化设计是提高结构性能和效益的重要手段。
工程力学中的杆件受力分析在建筑设计中的应用工程力学是应用力学原理研究和解决工程问题的学科,而杆件受力分析则是工程力学的重要内容之一。
在建筑设计中,杆件受力分析被广泛应用于结构设计、荷载计算和材料选择等方面。
本文将探讨工程力学中的杆件受力分析在建筑设计中的应用,并解释其重要性和优势。
1. 引言工程力学是一个涵盖广泛的学科,它揭示了物体在受力情况下的运动和变形规律。
其中,杆件受力分析是解决实际工程中杆件受力情况的关键。
杆件受力分析在建筑设计中起着至关重要的作用,它能帮助工程师评估结构的稳定性、确定荷载分布,并为材料选择提供依据。
2. 结构设计在建筑设计中,结构设计是至关重要的一环。
杆件受力分析可以帮助工程师确定结构中各个杆件的受力情况,从而优化结构设计方案。
通过分析每根杆件的受力,工程师可以评估其强度是否满足设计要求,是否需要进行增强或者替换。
杆件受力分析还可以帮助工程师检测结构中存在的潜在问题,如过大的应力集中、过度挠度等,从而及早采取相应的措施,确保结构的安全可靠。
3. 荷载计算荷载计算是建筑设计过程中的重要环节,它确定了结构所需承受的各种荷载。
工程力学中的杆件受力分析能够帮助工程师准确计算结构在不同工况下的荷载分布。
通过对每个杆件的受力分析,结合力的平衡和力矩平衡原理,工程师可以计算出各个杆件所承受的荷载大小和作用位置。
这些准确的荷载数据将有助于工程师制定合理的结构设计方案,确保结构在承受实际荷载时的安全性和稳定性。
4. 材料选择在建筑设计中,材料的选择对结构的性能和安全性有着重要影响。
工程力学中的杆件受力分析可以为材料选择提供依据。
通过对杆件受力状态的分析,工程师可以确定各个杆件所需的强度和刚度,并依此选择合适的材料。
杆件受力分析还可以评估材料的疲劳寿命,从而确保结构在长期使用中不会发生失效。
5. 结论工程力学中的杆件受力分析在建筑设计中扮演着重要角色。
它可以帮助工程师确定结构的稳定性、优化结构设计方案,并为荷载计算和材料选择提供依据。
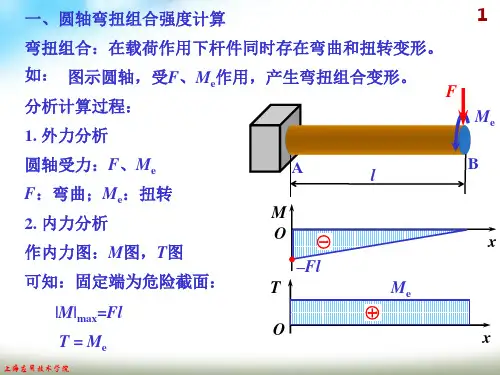
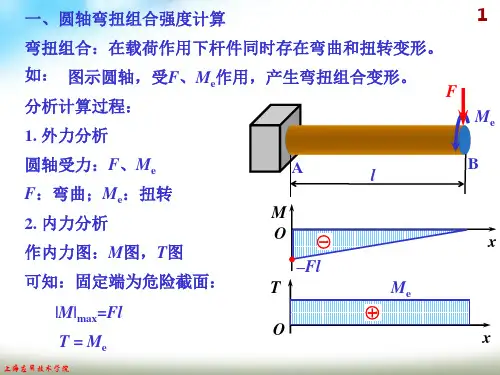
教学设计三
杆件弯曲受力分析计算
在学习绘制杆件弯曲受力分析图后,我们来学习一下杆件的弯曲受力分析计算,即我们杆件弯曲时在横截面上产生的弯曲正应力和弯曲剪应力的计算。
问题一,杆件弯曲横截面正应力计算问题
梁在弯曲变形时,梁轴线方向截面纤维曲线,下部拉伸变长,上部压缩变短。
我们选取杆件的某段横截面,其截面上某处的微分段面积dA如图8.2所示。
由该截面的积分得到,截面为弯矩M大小为公式8.1。
(公式8.1)根据广义胡可定律得到公式8.2与弯曲应变几何条件分析公式8.3得到公式8.4。
(公式8.2)
(公式8.3)
(公式8.4)
其中,ρ为梁弯曲的曲率半径。
将公式8.4和8.1合并得到公式8.5。
(公式8.5)分析公式8.5,其中:
为截面绕Z轴的惯性矩。
公式8.5变形为8.6。
ρ
ρ
ρ
ρ
ρ
ε
y
y
dx
dx
=
=
-
+
=
∆
=
dθ
dθ
dθ
dθ
y)dθ
(
⎰⋅
=
A
y
M dA
σ
ε
σ⋅
=E
ρ
ε
σ
y
E
E=
=
⎰
⎰⎰=
⎪⎪
⎭
⎫
⎝
⎛
=
⋅
=
A
A A
y
E
y
y
E
y
M dA
dA
dA2
ρ
ρ
σ
Z
A
I
y=
⎰dA2
(公式8.6)
将公式8.6与公式8.4合并,得到公式8.7
(公式8.7)
公式8.7为杆件弯曲截面上弯曲正应力一般计算公式。
如图8.2所示,y 为惯性轴到所计算应力位置的距离,分析公式我们发现当y 为0时,截面正应力为零,当y 等于截面高度一半时,截面正应力最大,说明在杆件中间有一条纤维线在受力弯曲时既不拉伸变长也不压缩变短,我们称这条纤维曲线为杆件的中性轴,此轴所在的水平层称为中性层,而在杆件截面上下边缘处,存在最大弯曲拉应力和最大弯曲压应力,也就是极值问题的出现。
我们引入新的物理量W ,抗弯截面模量,它的计算式为8.8。
(公式8.8)
公式8.7可以化简为极值公式8.9。
(公式8.9)
例题分析讲解 【例1】
图8.3所示,悬臂矩形截面杆件,截面O 1上有A 、B 、C 、D 点,求它们的弯曲正应力。
【解】
计算悬臂梁的弯矩
计算梁截面的惯性矩
计算抗弯截面模量 计算各点的正应力
y
I
W Z
=m kN 6.488.1302
1
2⋅=⨯⨯=M 001067
.0124.02.01233=⨯==bh I 00533.012
4.02.062
2=⨯==bh W Z W
M Z =
σZ
Z I E M ⋅=
ρ
1
y I M Z
Z
=
σ
(拉)MPa 12.900533
.06
.48===
Z Z a W M σ(压)
m 9.12kN a d ⋅=-=σσ0
b =σ(压)4.55MPa 0.11067
00.06
.48b c =⨯==
y I M Z Z σ
问题二,杆件弯曲横截面剪应力计算问题
与弯曲正应力不同,在截面上各点的弯曲剪应力指向相同,不论是否在中性层的上侧还是下侧;在同一剪力段,同一层的各点剪应力大小相同。
剪应力大小跟截面尺寸和形状有关,不同截面形式在相同外力作用下产生的剪应力是不同的,下面我们学习几种截面形式下的剪应力计算公式。
矩形截面杆件截面弯曲剪应力一般计算公式8.10:
(公式8.10)
(V y 梁截面剪力;S z 计算截面形心到梁截面形心的面积矩;I z 梁截面的惯性矩,b 梁截面宽度)
与弯曲正应力相似,在截面内也存在剪应力最大值,矩形截面杆件上弯曲剪应力分布成二次抛物线状,最大值在截面中性层处,上下边缘处为零,其极值计算公式8.11:
(公式8.11)
我们再来学习下圆形截面和圆环截面的弯曲剪应力计算式 对于圆形截面计算公式8.12:
(公式8.12)
对于圆环形截面计算公式8.13:
(公式8.13)
其中:A 为圆形或圆环截面面积
b
I S V z z y y =
τbh
V
y
max .y 23⋅=τA
V
y
max .y 34⋅=τA
V y max .y 2⋅
=τ
例题分析讲解
【例3】
图8.6所示,矩形截面梁收到集中力作用,求截面D上a点处的弯曲剪应力τa和全梁的最大剪应力τmax。
【解】
画出受力分析简图,计算D截面的剪应力V D
计算截面最大剪应力:
kN
20
=
D
V
MPa
8.1
10
6
10
12
10
6
10
5.4
1
6
10
20
2
8
3
6
3
a
=
⨯
⨯
⨯
⨯
⨯
⨯
⨯
⨯
⨯
=
=
-
-
-
b
I
S
V
Z
a
D
τ
MPa
33
.3
10
10
6
10
20
5.1
2
3
4
3
D.max
=
⨯
⨯
⨯
⨯
=
⋅
=
-
bh
V
D
τ
V
V D=20kN
V D=20kN。