四色循环

空间四色定理全文共四篇示例，供读者参考第一篇示例：空间四色定理是一种关于地图着色的数学定理，它指出任何平面图都可以用四种颜色进行着色，使得相邻的区域颜色不同。

这个定理是对四色定理在三维空间的推广，是由英国数学家哈佛·约瑟夫·萨福德和其学生乔治·法莫斯于1976年首次提出的。

在平面地图着色中，我们可以将地图上的不同区域用不同的颜色进行着色，但是要求相邻的区域颜色不能相同。

四色定理指出，任何一个平面图都可以用四种颜色进行着色，使得相邻的区域不会相同，即使图形非常复杂也是如此。

而空间四色定理则是在平面图的基础上推广到了三维空间，也就是说对于任意的三维几何图形或者复杂的几何体，我们也可以用四种颜色进行着色，使得相邻的部分颜色不同。

这个定理在实际应用中具有非常广泛的意义，可以被应用于地图着色问题、计算机图形学、密码学等领域。

对于空间四色定理的证明是非常复杂和困难的，因为三维空间的几何形状比平面图形更加复杂，其结构也更为多样化。

萨福德和法莫斯在提出这个定理之后，并没有给出详细的证明方法，而是留下了一个给数学家们解决的难题。

直到1982年，美国数学家凯恩·麦克蒂基成功地证明了空间四色定理，他在证明中使用了复杂的数学方法和技巧，包括拓扑学、图论、组合数学等。

这个证明过程非常漫长和复杂，耗费了大量的时间和精力。

空间四色定理的证明对于数学领域的发展具有重要的意义，它不仅解决了一个重要的数学难题，而且对于数学的推理和证明方法也有着深远的影响。

这个定理的提出和证明，为数学家们提供了一个全新的研究方向，也激发了更多的数学思考和探索。

空间四色定理是一个非常重要的数学定理，它指出了在三维空间中对图形着色的规律，为地图着色问题、计算机图形学等领域提供了有力的理论支持。

虽然证明过程非常困难，但是通过数学家们的辛苦努力，最终成功解决了这个难题，为数学领域的发展做出了重要的贡献。

希望这个定理能够继续激发更多人对数学的兴趣和热爱，推动数学领域不断发展和进步。

印刷基础理论－四色及网点介绍四色印刷:只要Ｒ+Ｇ+Ｂ三色按比例相撞能生成何止千万色.哪为什么要黑色呢?对,Ｒ.Ｇ.Ｂ比例相等时就能产生黑色,但是要三种油墨才能生成一种色,从经济角度看是行不通的.而实际上在设计的过程中黑色的运用是非常之多,这其实就是为什么要用四色印刷.还有一点:ＲＧＢ生成的黑色与用油墨直接调配而得的黑色相比之后,前者有一种虚浮感,而后者就感觉较沉实.１.有了四色原理大家就容易接受得多了.它相当于输出时的四张胶片,亦相当于PHOTOSHOP里面的channels中cyan,magenta,yellow,black(C,M,Y,K)四条通道.我们处理图像时对通道的修改,实际就是对胶片的改变.2.网目网点网角平网和挂网. 网目:每平方英寸,所放的网点数目,常用印刷品用175目,报纸用60目到100目不等,视纸质而定.特殊印刷有特殊的网目,视质地而定.网点:分圆形.椭圆.菱形.方形.钻石形.调频网点等.网角:最紧密相连的网点形成的直线与水平线的夹角角度.有30度，45度，75度，90（0）度。

平网:整块胶片的网点都是有规律平均分布的且大小一样,有如一个平面,没有层次感.上图就是平网挂网:网点大小不一样,网片有层次感)输出菲林前应该做些什么一、文件的格式现输出中心大部份采用方正栅格世纪RIP(pspnt）输出系统，及HQ510、以色列的赛天使、海德堡等照排输出系统。

全都支持postscrit打印机描述文件。

也就是后缀名为.ps的文件。

其它常见的可以直接RIP输出的文件格式有：s2、s72、ps2（方正书版）、EPS、TIF、PDF等。

目前较普遍使用的设计软件：photoshop、pagemaker、coreldraw、illustrator等，都可通过postscrip虚拟打印机生成一个PS文件或是PDF文件，而像方正书版、维思、飞腾等一些方正软件所生成的s2、ps2、ps文件，也可直接在方正世纪RIP输出，但其它输出系统就不支持。

四色印刷机工作原理
四色印刷机工作原理是指利用四种基本颜色油墨（青色、洋红色、黄色和黑色）通过特定的印刷过程相互叠加混合，以最大限度地还原所需色彩的印刷技术。

具体的工作原理如下：
1. 设计和准备：首先，设计师使用计算机软件创建印刷品的图像或设计。

然后，图像将被分解成四个颜色通道（青色、洋红色、黄色和黑色），每个通道代表一个油墨颜色。

2. 制版：将每个颜色通道的图像分别转换成印刷版。

这通常通过将图像分解成小点来实现，每个点的大小和空隙会影响油墨的量和色彩饱和度。

3. 印刷：在印刷过程中，四个印刷版按照特定的次序，一张接一张地被输出到印刷机上。

a. 静态印刷：每个颜色通道对应一种油墨，油墨被应用到不
同的印刷滚筒上。

印刷滚筒上涂满的油墨通过印刷版的网点和图案传输到印刷纸上。

b. 动态印刷：整个印刷过程中，印刷滚筒和印刷纸都在不断
地移动。

每个颜色通道的油墨被连续地应用和叠加在印刷纸上。

4. 叠加和混合：随着四个颜色通道的油墨逐渐叠加在印刷纸上，它们在视觉上混合成各种中间色和细节。

通过控制每个油墨的数量和位置，印刷机能够准确地还原出设计师所要表达的色彩。

总之，四色印刷机通过使用青色、洋红色、黄色和黑色这四种基本颜色油墨，通过特定的印刷过程相互叠加混合，以还原所需色彩的印刷品。

这种工作原理被广泛应用于许多领域，如平面印刷、包装印刷等。

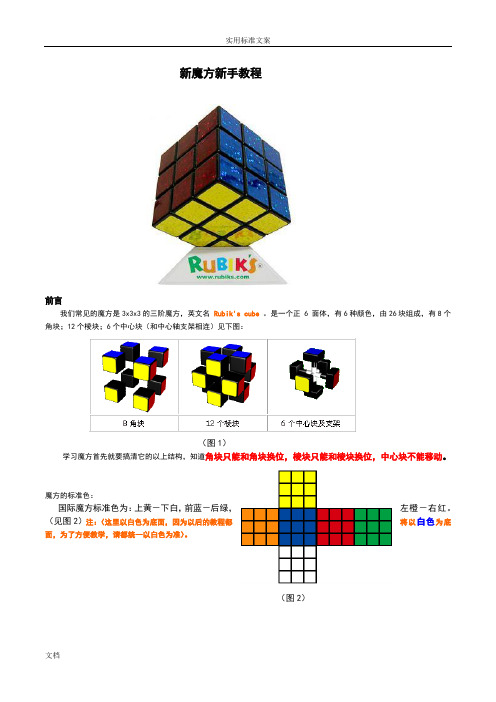
新魔方新手教程前言我们常见的魔方是3x3x3的三阶魔方，英文名Rubik's cube。

是一个正 6 面体，有6种颜色，由26块组成，有8个角块；12个棱块；6个中心块（和中心轴支架相连）见下图：（图1）学习魔方首先就要搞清它的以上结构，知道角块只能和角块换位，棱块只能和棱块换位，中心块不能移动。

魔方的标准色：国际魔方标准色为：上黄－下白，前蓝－后绿，左橙－右红。

（见图2）注：（这里以白色为底面，因为以后的教程都将以白色为底面，为了方便教学，请都统一以白色为准）。

（图2）认识公式（图3）（图4）公式说明：实际上就是以上下左右前后的英文的单词的头一个大写字母表示（图5）（图6）（图7）（图8）步骤一、完成一层首先要做的是区分一层和一面：很多初学者对于“一面”与“一层”缺乏清楚的认识，所以在这里特别解释一下。

所谓一层,就是在完成一面(如图2的白色面)的基础上,白色面的四条边,每条边的侧面只有一种颜色,图(2).如图（1）中心块是蓝色，则它所在面的角和棱全都是蓝色，是图(2)的反方向图（3）和（4）则是仅仅是一面的状态,而不是一层!（1）（2）（3）（4）注：图（2）和（4）分别是图（1）和（3）的底面状态想完成魔方，基础是最重要的，就像建筑一样，魔方也如此，基础是最重要的。

由于上文提到过中心块的固定性，这一性质，在魔方上实质起着定位的作用，简单的说就是中心块的颜色就代表它所在的面的颜色。

一、十字（就是快速法中的CROSS）第一种情况如图所示：公式为R2第二种情况如图所示：（白色下面颜色为橙色，为方便观察，特意翻出颜色）橙白块要移到上右的位置，现在橙白块在目标位置的下面。

但其橙色片没有和橙色的中心块贴在一起。

为此我们先做D ’ F ’ 即把橙色粘在一起，接着R 还原到顶层,，F是把蓝白橙还原到正确的位置(上面的F ’ 使蓝白块向左移了九十度)。

公式为D’ F ’ R F图解：当然，架十字不只只有上面两种情况，现我们在分析下其它的一些情况吧！ 如下图：橙白块的位置己对好，但颜色反了，我就先做R2化成第二种情况，然后用还原第二种情况的公式即可！（橙色下面颜色为白色，为方便观察，特意翻出颜色）上面两种情况都为前右的块要移到上后的位置。

电子技术课程设计题目：四路彩灯控制系统专业：本电气自动化班级：101姓名：姚远鹏学号：01 指导老师：李国平小组成员：姚远鹏邹志强梁钺成绩：四色循环彩灯控制设计摘要本设计共用了六块芯片实现了循环彩灯的功能. 通过外接一个5V的直流电源，减少变压整流步骤，简化了电源。

以计数器和位移寄存器作为核心器件,采用几个基本的数字集成的74系列（74LS93,74LS153,555）芯片来完成所需要的数字逻辑显示功能。

用555定时器，产生振荡信号，为计数器和位移寄存器提供工作脉冲；用D触发器自动控制彩灯的花样作为控制电路；用了双色发光二极管作为显示电路，发出发红色和绿色两色光，这也是本电路的特点。

关键字：计数器数据选择器移位寄存器彩灯显示电路—————————————目录第一章．.课程设计任务书 (4)1.1．设计题目 (4)1.2．课题意义 (4)1.3.设计要求 (4)1.4.设计内容 (4)1.5.课题实现方法 (4)第二章．设计任务和要求 (6)第三章．所用元件清单 (7)第四章．方案设计与单元设计 (8)4.1基本原理 (8)4.2．单元电路 (9)第五章．总电路图的设计 (14)5.1．工作原理 (14)5.2仿真的总电路图 (15)第六章．学习心得 (16)第七章．参考文献 (17)课程设计任务书2011-2012学年第二学期1.1．设计题目：完成期限：自2012年6月1日至2012年6月14日共两周设计依据、要求及主要内容：1.2．课题意义：本课题利用电子技术知识设计出彩灯装饰控制器，该控制器有4路输出，该输出不是简单的4路彩灯依次循环点亮，而是产生多种花样，它能使4路彩灯以“依次点亮——递增点亮——闪亮…….”等多种花样闪烁，可用于家和商铺的节日装饰。

通过本课题练习，学生对综合知识应用能力、设计能力将有较大提高，对今后从事电子产品的研制、生产、经营维修等打下基础。

1.3、课题实现方法：本课题利用电子技术设计节日装饰彩灯电路，可以先查阅相关资料（网上查找或参考相关书籍手册）；在理解的基础上确定设计方案，赃出完整的电路，提交课程设计说明书一份。

四循环可降解标志
1. 基本信息：
- 标志名称：四循环可降解标志
- 图标形状：圆形
- 图案颜色：绿色、蓝色和白色
- 标志背景颜色：白色
2. 图案设计：
- 标志中央为一个生态环，代表可持续发展和环保
- 环内部分画有四个相互连通的箭头环，代表循环利用与再生
- 箭头环的颜色依次为绿色、蓝色，象征可降解材料
3. 标志含义：
- 四循环：指循环利用、再生、降解和资源再生利用的四个循环过程
- 可降解：表示标志所代表的材料或产品可在自然条件下分解和降解，减少对环境的影响
- 标志传达对环境保护的关注，鼓励使用可循环再生、可降解的材料和产品
4. 使用范围：
- 标志适用于各类可循环再生和可降解的材料、制品、包装、纸张、塑料制品等
- 可用于产品包装、标签、广告宣传、产品认证等方面
5. 使用建议：
- 建议生产商在符合相关标准和认证要求的产品上标注该标志，以便消费者能够识别和选择可循环再生和可降解的产品
- 鼓励广大公众认识并采用可循环再生和可降解产品，共同推动环境保护与可持续发展
请注意：本标志仅作为一种指导性和宣传性的图形标识，具体认证和使用要遵循相关法律法规和标准的规定。

pdca循环运用例子在ASPICE标准的理解过程中，初学者常常面对纷繁复杂的过程实践不知何从下手（Practice）——其中的265个基本实践（Base Practice）和42个通用实践（Generic Practice）分布在32个过程域、5个级别的框架中，各司其职又彼此关联。

如果不能用清晰的脉络厘清这些实践中的序列关系，很容易陷入“只见树木、不见森林”的处境。

在之前一篇ASPICE的解析文章《红绿蓝——ASPICE过程域的组织形式》中（以下为地址），用红绿蓝三色滤镜对ASPICE各个过程域组织形式的全貌做了整体的概览。

而在这一篇里将用PDCA四色分光镜对具体的实践进行解析。

从ASPICE3.1的《表E.1 —参考标准》来看（如下图），其来源无一例外地来自ISO族的标准（如ISO33020 / ISO12207等），而与ISO最广为人知的质量体系标准ISO9000系标准类似，它同样遵循着过程方法的原则(Process Approach)。

在众多方法论中，被广泛应用的“戴明环”PDCA同样在ASPICE的实践序列的定义中得到体现。

ASPICE3.1的《表E.1 —参考标准》在具体解析之前，我们先看看PDCA的定义——PDCA（Plan-Do-Check-Act的简称）循环式品质管理，针对品质工作按计划、执行、检查与行动来进行活动，以确保可靠度目标之达成，并进而促使品质持续改善。

由美国学者爱德华兹·戴明提出，因此也称戴明环。

这个四步的循环一般用来提高产品品质和改善产品生产过程。

（参考维基百科）了解了基本定义，我们随着这四个步骤，解读在ASPICE中，具体的过程域中是如何把这个过程方法的原则落地的，因为篇幅有限，本文讨论的是VDA范围的主要的工程过程域，即系统部分（SYS.2-SYS.5）和软件部分（SWE.1-SWE.6），以及相关的的项目管理部分（MAN.3）。

计划篇（Plan）建立明确的目标，并制定相关的计划和确定必要的程序。

四色定理四色定理(Four color theorem)最先是由一位叫古德里（Francis Guthrie）的英国大学生提出来的。

德·摩尔根（Augustus De Morgan，1806～1871）1852年10月23日致哈密顿的一封信提供了有关四色定理来源的最原始的记载。

四色问题又称四色猜想，是世界近代三大数学难题之一。

基本介绍四色问题又称四色猜想、四色定理是世界近代三大数学难题之一。

地图四色定理(Four color theorem)最先是由一位叫古德里FrancisGuthrie的英国大学生提出来的。

德·摩尔根Augustus De Morgan180618711852年10月23日致哈密顿的一封信提供了有关四色定理来源的最原始的记载。

他在信中简述了自己证明四色定理的设想与感受。

一个多世纪以来数学家们为证明这条定理绞尽脑汁所引进的概念与方法刺激了拓扑学与图论的生长、发展。

1976年美国数学家阿佩尔K.Appel与哈肯W.Haken宣告借助电子计算机获得了四色定理的证明又为用计算机证明数学定理开拓了前景。

地图四色定理(Four color theorem)最先是由一位叫古德里Francis Guthrie的英国大学生提出来的。

四色问题的内容是“任何一张地图只用四种颜色就能使具有共同边界的国家着上不同的颜色。

”用数学语言表示即“将平面任意地细分为不相重叠的区域每一个区域总可以用1234这四个数字之一来标记而不会使相邻的两个区域得到相同的数字。

”这里所指的相邻区域是指有一整段边界是公共的。

如果两个区域只相遇于一点或有限多点就不叫相邻的。

因为用相同的颜色给它们着色不会引起混淆。

四色问题的内容是“任何一张地图只用四种颜色就能使具有共同边界的国家着上不同的颜色。

”也就是说在不引起混淆的情况下一张地图只需四种颜色来标记就行发展历史：来自地图的启示相传四色问题是一名英国绘图员提出来的此人叫格思里。

四色原理简介这是一个拓扑学问题，即找出给球面（或平面）地图着色时所需用的不同颜色的最小数目。

着色时要使得没有两个相邻（即有公共边界线段）的区域有相同的颜色。

1852年英国的格思里推测：四种颜色是充分必要的。

1878年英国数学家凯利在一次数学家会议上呼吁大家注意解决这个问题。

直到1976年，美国数学家阿佩哈尔、哈肯和考西利用高速电子计算机运算了1200个小时，才证明了格思里的推测。

四色问题的解决在数学研究方法上的突破，开辟了机器证明的美好前景。

四色定理的诞生过程世界近代三大数学难题之一(另外两个是费马定理和哥德巴赫猜想)。

四色猜想的提出来自英国。

1852年，毕业于伦敦大学的弗南西斯·格思里(Francis Guthrie)来到一家科研单位搞地图着色工作时，发现了一种有趣的现象：“看来，每幅地图都可以用四种颜色着色，使得有共同边界的国家着上不同的颜色。

”,用数学语言表示，即“将平面任意地细分为不相重迭的区域，每一个区域总可以用1，2，3，4这四个数字之一来标记，而不会使相邻的两个区域得到相同的数字。

”这个结论能不能从数学上加以严格证明呢？他和在大学读书的弟弟格里斯决心试一试。

兄弟二人为证明这一问题而使用的稿纸已经堆了一大叠，可是研究工作没有进展。

1852年10月23日，他的弟弟就这个问题的证明请教他的老师、著名数学家德·摩尔根，摩尔根也没有能找到解决这个问题的途径，于是写信向自己的好友、著名数学家哈密尔顿爵士请教。

哈密尔顿接到摩尔根的信后，对四色问题进行论证。

但直到1 865年哈密尔顿逝世为止，问题也没有能够解决。

1872年，英国当时最著名的数学家凯利正式向伦敦数学学会提出了这个问题，于是四色猜想成了世界数学界关注的问题。

世界上许多一流的数学家都纷纷参加了四色猜想的大会战。

1878～1880年两年间，著名的律师兼数学家肯普和泰勒两人分别提交了证明四色猜想的论文，宣布证明了四色定理，大家都认为四色猜想从此也就解决了。