第二章固体的结合
- 格式:ppt
- 大小:885.50 KB
- 文档页数:36

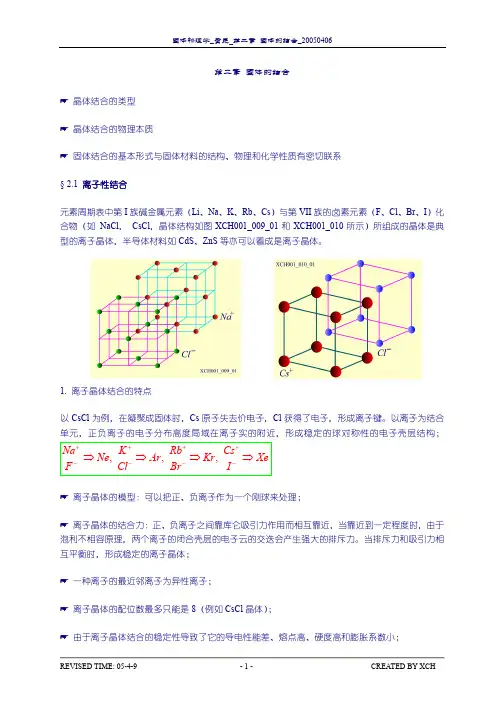
第二章 固体的结合晶体结合的类型 晶体结合的物理本质固体结合的基本形式与固体材料的结构、物理和化学性质有密切联系 § 2.1 离子性结合元素周期表中第I 族碱金属元素(Li 、Na 、K 、Rb 、Cs )与第VII 族的卤素元素(F 、Cl 、Br 、I )化合物(如 NaCl , CsCl ,晶体结构如图XCH001_009_01和XCH001_010所示)所组成的晶体是典型的离子晶体,半导体材料如CdS 、ZnS 等亦可以看成是离子晶体。
1. 离子晶体结合的特点以CsCl 为例,在凝聚成固体时,Cs 原子失去价电子,Cl 获得了电子,形成离子键。
以离子为结合单元,正负离子的电子分布高度局域在离子实的附近,形成稳定的球对称性的电子壳层结构;,,,Na K Rb Cs Ne Ar Kr Xe FClBrI++++−−−−⇒⇒⇒⇒离子晶体的模型:可以把正、负离子作为一个刚球来处理;离子晶体的结合力:正、负离子之间靠库仑吸引力作用而相互靠近,当靠近到一定程度时,由于泡利不相容原理,两个离子的闭合壳层的电子云的交迭会产生强大的排斥力。
当排斥力和吸引力相互平衡时,形成稳定的离子晶体; 一种离子的最近邻离子为异性离子;离子晶体的配位数最多只能是8(例如CsCl 晶体);由于离子晶体结合的稳定性导致了它的导电性能差、熔点高、硬度高和膨胀系数小;大多数离子晶体对可见光是透明的,在远红外区有一特征吸收峰。
氯化钠型(NaCl 、KCl 、AgBr 、PbS 、MgO)(配位数6) 氯化铯型(CsCl 、 TlBr 、 TlI)(配位数8)离子结合成分较大的半导体材料ZnS 等(配位数4) 2. 离子晶体结合的性质 1)系统内能的计算晶体内能为所有离子之间的相互吸引库仑能和重叠排斥能之和。
以NaCl 晶体为例,r 为相邻正负离子的距离,一个正离子的平均库仑能:∑++−++321321,,2/122322222102)(4)1('21n n n n n n r n r n r n q πε ——遍及所有正负离子,因子1/2—库仑作用为两个离子所共有,一个离子的库伦能为相互作用能的一半。
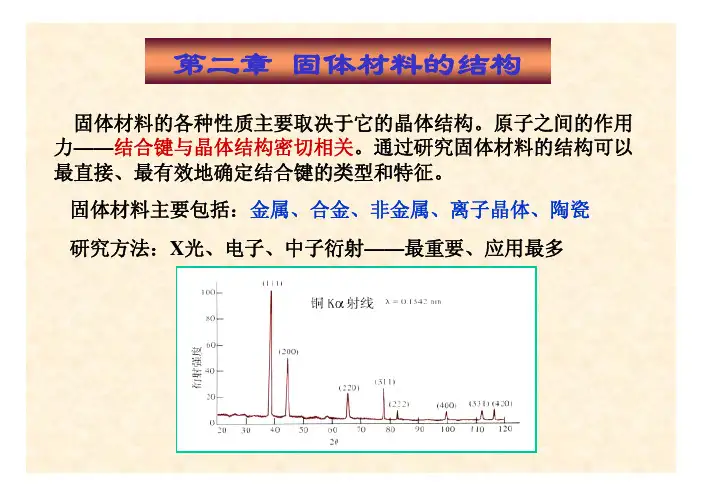
第二章固体材料的结构固体材料的各种性质主要取决于它的晶体结构。
原子之间的作用结合键与晶体结构密切相关。
通过研究固体材料的结构可以最直接、最有效地确定结合键的类型和特征。
固体材料主要包括:金属、合金、非金属、离子晶体、陶瓷研究方法:X光、电子、中子衍射——最重要、应用最多§2-1 结合键结合键——原子结合成分子或固体的结合键决定了物质的物理、化学、力学性质。
一切原子之间的结合力都起源于原子核与电子间的静电交互作用(库仑力)。
不同的结合键代表了实现结构)的不同方式。
一、离子键典型的金属与典型的非金属元素就是通过离子键而化合的。
从而形成离子化合物或离子晶体由共价键方向性特点决定了的SiO2四面体晶体结构极性共价键非极性共价键五、氢键含有氢的分子都是通过极性共价键结合,极性分子之间结合成晶体时,通过氢键结合。
例如:H 2O ,HF ,NH 3等固态冰液态水§2-2 金属原子间的结合能一、原子作用模型固态金属相邻二个原子之间存在两种相互作用:a) 相互吸引——自由电子吸引金属正离子,长程力;b) 相互排斥——金属正离子之间的相互排斥,短程力。
平衡时这二个力相互抵消,原子受力为0,原子处于能量最低状态。
此时原子间的距离为r0。
§2-3 合金相结构基本概念♦合金——由两种或两种以上的金属或金属非金属元素通过化学键结合而组成的具有金属特性的材料。
♦组元、元——组成合金的元素。
♦相——具有相同的成分或连续变化、结构和性能的区域。
♦组织——合金发生转变(反应)的结果,可以包含若干个不同的相,一般只有一到二个相。
♦合金成分表示法:(1) 重量(质量)百分数A-B二元合金为例m B——元素B的重量(质量m A——元素A的重量(质量合金中的相分为:固溶体,化合物两大类。
固溶体金属晶体(溶剂)中溶入了其它元素(溶质)后,就称为固溶体。
一、固溶体的分类:♦按溶质原子在溶剂中的位置分为:置换固溶体,间隙固溶体♦按溶解度分为:有限固溶体,无限固溶体♦按溶质原子在溶剂中的分布规律分为:有序固溶体,无序固溶体置换固溶体:溶质原子置换了溶剂点阵中部分溶剂原子。








《固体物理学》习题解答黄昆 原著 韩汝琦改编 (陈志远解答,仅供参考)第一章 晶体结构1.1、解:实验表明,很多元素的原子或离子都具有或接近于球形对称结构。
因此,可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。
这样,一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。
它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比,即:晶体原胞的空间利用率, VcnVx = (1)对于简立方结构:(见教材P2图1-1)a=2r , V=3r 34π,Vc=a 3,n=1 ∴52.06r 8r34a r 34x 3333=π=π=π= (2)对于体心立方:晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)r 334(r 342a r 342x 3333≈π=π⨯=π⨯=(3)对于面心立方:晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4,Vc=a 374.062)r 22(r 344a r 344x 3333≈π=π⨯=π⨯= (4)对于六角密排:a=2r 晶胞面积:S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233 晶胞的体积:V=332r 224a 23a 38a 233C S ==⨯=⨯ n=1232126112+⨯+⨯=6个 74.062r224r 346x 33≈π=π⨯= (5)对于金刚石结构,晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 334.063r 338r 348a r 348x 33333≈π=π⨯=π⨯=1.2、试证:六方密排堆积结构中633.1)38(a c 2/1≈= 证明:在六角密堆积结构中,第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形,第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切,于是: NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。