当前位置：文档之家 › 西北太平洋热带气旋

西北太平洋热带气旋

  • 格式：doc
  • 大小：930.64 KB
  • 文档页数：17

下载文档原格式

  / 17

合集下载

热带MJO和ENSO对西北太平洋热带气旋影响研究综述

热带MJO和ENSO对西北太平洋热带气旋影响研究综述

摘要
对 西 北 太 平 洋 热 带 气 旋 的 活 动 规 律 作 了综 合 评 述 ， 单 回 顾 了 热 带 季 节 内 振 荡 （ Ｏ） 征 和 厄 尔 尼 诺 ／ 简 ＭＪ 特 南
方 涛 动 （ ＮＳ 特 征 以 及 两 者 间 关 系 ， 系统 地 总 结 了 近 年 来 国内 外 学 者 关 于 ＭＪ 和 Ｅ Ｏ对 西北 太平 洋 海 域 热 Ｅ Ｏ） 较 Ｏ ＮＳ
气旋 活动 也具有 和 Ｅ Ｏ循 环 相 近 的 ３ ＮＳ ～４年周 期 的年际 变化 。此 外 ， 国是 受 台 风危 害最 为 严 重 的 我
低 南方涛动指 数 特征 ， 包括 赤道 东 太平 洋 暖水 （ ｌ 又 Ｅ
Ｎｉｏ 和冷水 事 件 （ ａＮｉａ ， 这 些 事 件 发 生 都 有 ｎ） Ｌ ｎ ）且
间尺度 介于月 、 季之 问 ， 因而与 长期 天气 变化 和短期
旋 ， 中 ８ ％发 展成 热带 风暴 或 台风 。热 带 气旋 生 其 Ｏ 成 存 在显 著季 节变 化 ， 秋 两 季 集 中 了全 年 热带 气 夏 旋 频 数 的 ８ 。热 带 气 旋 生 成 时 间 也 呈 活 跃 期 及 ０
Ｗａ ｅ 环 流 ， 致 赤 道 西太 平 洋对 流 活 跃 区东 移 到 ｌ ｒ ｋ 导 中太平洋 ， 雨 区东移 ｌ 。同 时 ， １ ｎ 年 西太平 洋 多 ＿ ７ ］ Ｅ ｏ Ｎｉ
３ 年 的准周期 。因此 ， ～７ 近年来又将 Ｅ Ｏ事件称 为 ＮＳ
Ｅ Ｓ Ｎ Ｏ循 环 ， 暖 状 态 和 冷 状 态 的 循 环 出 现ｌ 。 即 ｜ ５ ］
Ｅ Ｏ ＮＳ 是全球海洋 和 大气 相互作 用 最强 的信 号 ， 其爆
发结束 时间 、 发展 阶段 和强 度及类型 的不 同都 会对全 球气候带来 明显影 响 ， 对热 带太平洋 地 区影 响最为直 接和强烈 ， 与赤道 中、 太平 洋 的增 暖 和信 风减 弱密 东

诡异台风

诡异台风

台风约克1999年的西北太平洋热带气旋台风约克(Typhoon York, 9915)于9月12日在菲律宾以东海面形成，横过吕宋北部以后进入南中国海向广东沿岸移动。

9月16日早上掠过香港南部之后横过珠江口在珠海登陆移入内陆。

台风约克掠过香港期间，香港天文台一度发出10号飓风讯号。

这是香港在1983年之后16年内首次发出最高的热带气旋警告讯号，亦是香港在整个90年代唯一一次，更是香港回归中国以来第一次。

约克在香港造成2人死亡，约500人受伤，直接经济损失约10亿港元。

约克在菲律宾亦造成山泥倾泻，引致18人死亡。

在珠海及邻近广东省，约克造成15人死亡，700人受伤。

澳门亦有1人受伤。

形成及路径9月12日，马尼拉东北420公里之太平洋海面一个热带低气压向西移动，横过吕宋北部以后进入南中国海，之后在13日加强为一热带风暴，命名为约克。

约克在南中国海向北移动，在14日加强成一强烈热带风暴，然后改向西北移动。

15日下午，约克几乎停留不动，同时加强成为一台风。

直至深夜方再开始向西北方向移动。

翌日早上，约克掠过香港南部，之后在珠江口西岸移入内陆。

吹袭香港过程香港天文台在9月13日10:45，约克在香港东南650公里时发出1号戒备讯号。

14日香港吹和缓北风，间中有骤雨。

15日10:15天文台改发3号强风讯号。

当天下午约克几乎停留不动，直至晚上香港风势加强，天文台在16日03:15改发8号西北烈风或暴风讯号；之后在05:20改发9号烈风或暴风风力增强讯号，并且在06:45发出10号飓风讯号。

约克最接近香港是在当天10:00，当时其中心位于天文台西南偏南20公里。

约克中心掠过香港南部之南丫岛，长洲，最后经过大屿山进入珠江口。

10号飓风讯号维持了11小时，至17:45解除，以8号西南烈风及暴风讯号取代；是香港纪录上最长的一次。

其间香港东南之外岛横澜岛录得一小时平均风速151公里，而阵风更达234公里，是该气象站纪录。

长洲亦录得飓风，最高1小时平均112公里，阵风182公里。

大气科学概论-第四讲(热带气旋)

大气科学概论-第四讲(热带气旋)

已“退休”的热带气旋的名字：
2006年的16号强台风“象神”（Xangsane），在菲 律宾、海南、越南、柬埔寨、泰国总共造成279人死 亡以及7.47亿美元的损失。 2006年的22号超强台风“榴莲”（Durian），在菲 律宾、越南、泰国总共造成于819人死亡，经济损失 之大无法估计。
2005年的9号强台风“麦莎”（Metsa），给我国华 东地区造成大损失。
2004年的14号强台风“云娜”（Rainne），造成我国 东部沿海大的人员伤亡。
2003年的7号超强台风“伊布都”（Imouto），造成 菲律宾，华南大的人员伤亡。
2004年8月，台风“云娜”登陆 浙江。虽然气象局及时预报， 但仍造成115人死亡，1800人受 伤，经济损失达到￥1530亿。
已“退休”的热带气旋的名字：
16% 11% 10% 3% 3% 10% 11%
主要在8-9月 主要在1-3月 主要在春秋季节 主要在春秋季节 主要在1-3月 主要在1-3月 其中9月最多
影响我国的台风多发源于西北太平洋和南海 地区，平均每年有7～8个台风在我国登陆， 登陆的时间在5～11月， 主要集中在7～9月， 就登陆地段而言，南起 海南北至辽东半岛 均可有台风登陆。
3. 垂直方向风速不能相差太大：上下层 空气相对运动很小，才能使初始扰动中 水汽凝结所释放的潜热能集中保存在台 风眼区的空气柱中，形成并加强台风暖 中心结构；
台风空气运动的受力分析
这个结果表明台风的中心气压和最大风速是有限的
台风暖心结构的温度与高度分布 虚线表示等温线
热带气旋的三维空间结构
眼区Βιβλιοθήκη 9714号台风 （中国） Winnie 1997 （美国）
眼壁
外围螺旋带 状云系

西北太平洋热带气旋变性阶段强度变化的比较研究

西北太平洋热带气旋变性阶段强度变化的比较研究
槽 前 的急 流 相 互作 用 时 ， 高 空 急 流 入 口区 左 侧 和 出 口区 右 侧 的次 级 环 流 将 产 生高 空辐 散低 空辐 合 的趋 势 ，有 利 于
低层 Ｔ Ｃ低压 的发展 。同时，当 Ｙ ａ ｇ ｉ 在 穿越 急流的过程当中，垂直风切变的增加将导致斜压不稳定增强，低层锋
第３ ７卷 第 ４期
２ ０ １ ３年 ７月
大
气
科
学
Ｖｂ １ ．３ ７ ．Ｎｏ ．４
Ｊ ｕ １ ．２０１ ３
Ｃｈ ｉ ｎ ｅ ｓ ｅ Ｊ ｏｕ ｍａ ｌ ｏｆ Ａｔ ｍｏ ｓ ｐ ｈ ｅ ｒ ｉ ｃ Ｓｃ ｉ ｅ ｎ ｃ ｅ ｓ
应俊 ， 陈 光华 ， 黄荣辉， 等． ２ ０ １ ３ ． 西 北太 平洋 热 带气旋 变 性阶段 强度 变化 的比较研 究 ［ Ｊ ］ ． 大 气科 学， ３ ７ （ ４ ） ： ７ ７ ３ — ７ ８ ５ ， ｄ ｏ ｉ ： １ ０ ． ３ ８ ７ ８ ／ ｊ ． ｉ ｓ ｓ ｎ ． １ ０ ０ ６ － ９ ８ ９ ５ ． ２ ０ １ ２ ．
区强烈发展 ，锋 区内的斜压 能量 可能向 Ｔ Ｃ动 能转 化，从而 使得 Ｙ ａ ｇ ｉ 发展增强；（ ２ ）高空槽所对应 的高层湿位涡
下传可使得低层 正涡度增长 ，从而在低层诱生 出气旋性环流 ，有利于 Ｙ ａ ｇ ｉ 变性后重新 发展 ；（ ３ ）Ｙ ａ ｇ ｉ 与中纬度 原
先存在 的温带气旋 发生合 并，温 带气旋所带来的较高纬度冷空气 的入侵增强 了低层 的水平温度梯度 ，使得低层锋
２Ｃ ｅ ｎ ｔ ｅ ｒ ｆ ｏ ｒ Ｍｏ ｎ ｓ ｏ ｏ ｎ Ｓ ｙ ｓ ｔ ｅ ｎＲ ｒ ｅ ｓ ｅ ａ ｒ ｃ ｈ ， Ｉ ｎ ｓ ｔ ｉ ｔ ｕ ｔ ｅ ｏ ｆ Ａ ｔ ｍ ｏ ｓ ｐ ｈ ｅ ｒ ｉ ｃ Ｐ ｈ ｙ ｓ ｉ ｃ ｓ ， Ｃ ｈ ｉ ｎ ｅ ｓ ｅ Ａ ｃ ａ ｄ ｅ ｍ ｙｏ ｆ Ｓ ｃ ｉ ｅ ｎ ｃ ｅ ｓ ， Ｂ ｅ ｊ ｉ ｉ ｎ ｇ１ ０ ０ ０ ２ ９

西北太平洋热带气旋与上层海洋热含量的关系

西北太平洋热带气旋与上层海洋热含量的关系

ＡＣＴＡ ＯＣＥ ＡＮ ＯＬＯＧＩ ＣＡ Ｓ Ｉ ＮＩ ＣＡ
蔡 晓杰 ， 姜华 ， 王辉 ， 等 ．西 北 太平 洋热 带 气 旋 与上 层 海 洋 热含 量 的关 系 ［ Ｊ ］ ．海 洋学 报 ， ２ ０ １ ３ ， ３ ５ （ ３ ） ： ２ ８ —３ ５ ．
Ｃａ ｉ Ｘｉ ａ ｏ ｊ ｉ ｅ ， Ｊ ｉ ａ ｎ ｇ Ｈｕ ａ ，Ｗ ａ ｎ ｇ Ｈｕ ｉ ， ｅ ｔ ａ １ ．Ｔｈ ｅ ｒ ｅ ｌ ａ ｔ ｉ ｏ ｎ ｓ ｈ ｉ ｐ ｂ ｅ ｔ ｗｅ ｅ ｎ ｔ ｒ ｏ ｐ ｉ ｃ ａ ｌ ｃ ｙ ｃ ｌ ｏ ｎ ｅ ｉ ｎ ｔ ｈ ｅ ｎ ｏ ｒ ｔ ｈ ｗｅ ｓ ｔ Ｐａ ｃ ｉ ｆ ｉ ｃ ａ ｎ ｄ ｕ ｐ ｐ ｅ ｒ ｏ ｃ ｅ ａ ｎ ｈ ｅ ａ ｔ ｃ ｏ ｎ —
收稿 日期 ： ２ ０ １ ２ — ０ ８ ３ １ ； 修 订 日期 ： ２ ０ １ ３ — ０ １ — １ １ 。
基金 项 目： 国家 自然科 学 基 金 （ ４ ０ ９ ７ ６ ０ １ ４ ） ； 国 家海 洋 局公 益 项 目（ ２ ０ １ １ ０ ５ ０ １ ９ ） 。
中图 分 类 号 ： Ｐ ７ ３ ２ ． ６ 文 献标 志 码 ： Ａ 文 章编 号 ： ０ ２ ５ ３ — ４ １ ９ ３ （ ２ ０ １ ３ ） ０ ３ — ０ ０ ２ ８ — ０ ８
１ 引 言
西北太平 洋是全球热带 气旋形成最 活跃 的地 区 ， 也是 登陆 中国 台风 的主要 源地 。虽然 热 带气 旋 是 天 气 尺度过程 ， 但 已有 研 究发 现热 带 气旋 的发 生频 次 、
位 置的季节 和年 际变化 等 特征 与气 候 现象 有 密切 联 系 。研究结果 表明 ， 北太平洋 涛动 、 厄 尔尼诺 、 南极 涛

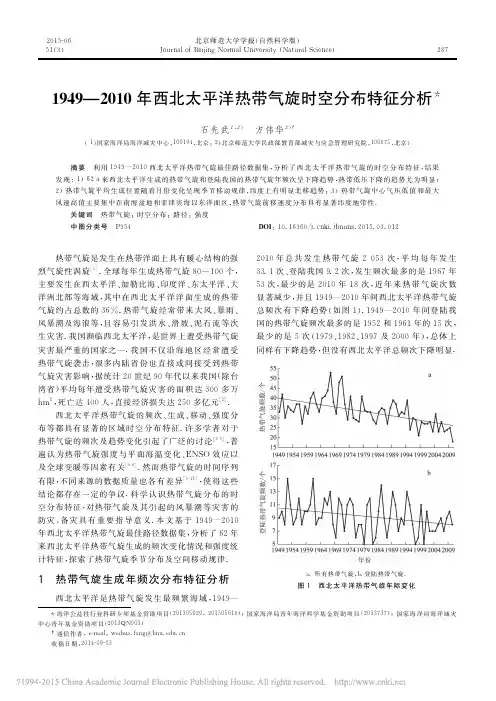
1949_2010年西北太平洋热带气旋时空分布特征分析_石先武

1949_2010年西北太平洋热带气旋时空分布特征分析_石先武

平洋热带气旋生成位置年均纬度呈显著的倒 “ 型分 Ｖ” 布， 从 ３—８ 月热带气 旋 生 成 位 置 不 断 北 移 ， 在８月以 后开始南移 ， 直至 ２—３ 月 达 到 最 南 ． 热带气旋生成主 的纬度区 ， 这一纬度带生成的热带气旋 占 要在 ５ ° ０ ° ～２ 北纬３ 以北历史上没有热带气旋生 总数 的 ８ １ ． ４％． ５ ° 成， 赤道附近有少量热带气旋生成 ． 经度的地带性并没 之外共有１ 有纬度那么明显 ， 研究区域 东 经 ０ ° ８ ０ ° ４ ～１ 次热带气旋生 成 ， 之间生成的热带气 东经１ ３ ０ ° ６ ０ ° ～１ 表 ３ 统 计 了 生 成 频 次 随 经 度、 旋占总数 的 近 ６ 月 ０％． 份的变化情况 ． 从表中可以发现 １—３ 月份热带气旋生 成于西北太平洋西侧 ， 而从 ３—６ 月热带气旋生成位置 不断西移 ， ６ 月份生成 位 置 最 靠 近 我 国 沿 海 地 区 ， ６月 份之后又不断向东移动 ．
占比例的年变化趋势 ． 从图 ２ 可看出 ， 西北太平洋热带 低压和超强台风所占 比 例 呈 现 明 显 下 降 趋 势 ， 热带风 暴和台风所占比例呈 上 升 趋 势 ， 强热带风暴和强台风 所占比例呈波动状态 ． 从图 ３ 可看出 ， 登陆我国的热带 风暴所占比例有上升 趋 势 ； 登陆我国的台风所占比例 主要是在当年 ７ 月份有 ５ 场台 在２ ０ ０ １ 年有一个峰值 ，
２ ， 死亡达 ４ 直接经济损失达 ２ ｍ ０ ０人， ５ ０ 多亿元 ２ ． ｈ 西北 太 平 洋 热 带 气 旋 的 频 次 、 生 成、 移 动、 强度分 ［］
平均每年发生 ２ ０ １ ０ 年总 共 发 生 热 带 气 旋 ２ ５ ３ 次， ０ 登陆我国 ９ 发生频次最多的是１ ３ ． １次、 ． ２次， ９ ６ ７年 ３ 最少的是 ２ 近年来热带气旋次数 ５ ３次， ０ １ ０年１ ８ 次， 显著减少 ， 并且 １ ９ ４ ９—２ ０ １ ０ 年间西北太平洋热带气旋 总频 次 有 下 降 趋 势 （ 如 图 １） １ ９ ４ ９—２ ０ １ ０年间登陆我 ． 国的热带气旋频次最多的是 １ ９ ５ ２和１ ９ ６ １ 年的 １ ５次， ， 最少 的 是 ５ 次 （ 总体上 ９ ７ ９、 １ ９ ８ ２、 １ ９ ９ ７及２ ０ ０ ０ 年） １ 同样有下降趋势 ， 但没有西北太平洋总频次下降明显 ．

北极涛动和南极涛动对西北太平洋热带气旋活动的影响


2000年、2007年、2010年和2011年）.
2西北太平洋TC活动与AO、AAO的变化特征
1979-2019年，西北太平洋生成TC共1237个，其中1979~1994年生成的TC偏多，年均生成34个 TC, 1989年和1994年达到峰值40个，远高于气候平均值；1995~2019年TC频数有下降趋势，年均生成 28个TC, 1998年和2010年分别仅生成21个和8个，远低于气候平均值（图1 （a） ） .TC生成主要月份集 中在6~11月，1~4月生成的TC仅占总频数的6.71%, 41年来8月份生成的TC共261个，2月份仅生成11个. TC生成源地在经度和纬度范围都存在相对集中的区域，主要分布在10。N~18.3° N、127° E~150° E. TC生成的纬度分布存在的季节性移动与太阳直射点的移动密切相关，体现了TC生成与活动的本质是地球 表面能量的运输与平衡的过程閃.不同强度的TC频数特征为TS>TY>S-TY>SUPER-TY>TD,随着TC强度的 增强，TC的生成源地越偏东偏南.
范丽君等分析AO指数（AOI）和AAO指数（AAOI）,发现在空间上两者都具有明显环状结构、在时 间上各季节有不同位相变化特征巴此外，A0在北半球夏季与冬季存在较大的时空特征差异，夏季A0从
收稿日期：2021-03-03 作者简介：陈仁容（1987-）,女，重庆巫山人，讲师，博士，主要研究方向：地貌与气候.
第39卷第3期
陈仁容，梁嘉欣，戚子琪，等北极涛动和南极涛动对西北太平洋热带气旋活动的影响
75
1970年左右开始出现准2年周期振荡吟現基于ipcc AR4耦合模式的模拟预估，AO和AAO在全球变暖背景
下将持续增强吧两大涛动的位相配置也受到关注，AO、AAO的反位相变化主要受到AO异常的影响，同

热带气旋

热带气旋的螺旋雨带通常有“主雨带（principle rainband）”、“次级雨带（secondary rainband）” 和“外围雨带（distant rainband）”之分 。其中主雨带也被称为“内雨带（inner rainband）”，是螺 旋雨带的主体部分，在气旋的运动过程中几乎与眼墙相对静止 ，在一些研究中被认为是热带气旋本体和环境的 分界 。次级雨带是围绕主雨带旋转的一组对流单体。外雨带可能沿气旋半径被逐步卷入主雨带中，也可能松散 地组织在热带气旋周围 。外围雨带是热带气旋最外侧的零星出现的对流系统的总和，在一些研究中也被称为 “外围中尺度对流系统（Outer Mesoscale Convective System, OMCS）” 。
4
温湿参量
5
能量参量
云系
热带气旋的云系是其动力学特征的固有表现，一般地，对流活动产生的直展云系在热带气旋的生成和发展阶 段具有处于中心地位 ；进入成熟期后，热带气旋也已直展云系为主，其内部包含有旋转的强上升气流和相对较 弱的下沉气流。层云可见于热带气旋的风眼，其垂直高度在边界层顶附近，上方是顶部下沉气流。眼墙云以积云 族为主，垂直高度可达对流层顶，卫星云图表现为中心密集云团区（Central Dense Overcast, CDO） 。
随着热带气旋生命阶段的变化，风眼的几何特征会发生改变。快速增强的热带气旋拥有小、清晰且高度对称 的风眼，有时被称为“针孔眼（pinhole eye）”、成熟期热带气旋拥有对称的圆形风眼，且风眼被连续的眼墙 包围，即“闭合眼（closed eye）” 。处于消亡期或发展不完全的热带气旋具有不规则的风眼，例如眼墙不 闭合（open eye）、形态不对称或残片状的风眼 。风眼的动态变化在热带气旋的业务天气预报中可作为参考 。

热带气旋


高层辐散流场叠置在低层扰动之上
要使低层扰动迅速发展，在低层辐合流场的上 空要有辐散流场，而且高空辐散必须大于低层 辐合。这种高空辐散流场的“抽吸作用”，保 证了对流层中、下层的上升运动，促使地面不 断降压，最后发展成热带气旋。
热带气旋的减弱、消亡和加强
热带气旋的减弱和消亡： 1. 登陆受地面摩擦、水汽源切断而减弱消亡。 2. 移到高纬，吸入冷空气或插入锋面，减弱变性或消亡。 3. 移入冷水面减弱或消亡。 热带气旋的加强： 1. 移向暖水面。 2. 登陆后重新回到海上。 3. 移速减慢。 4. 移到高空辐散区的下方。
热带气旋发生季节
季节：热带气旋一年四季均有发生，但绝大多数集中 在某几个月。北半球主要集中产生在7～10月，8～9月 最频繁；南半球主要集中产生在1～3月；孟加拉湾和 阿拉伯海主要产生在5月或10～11月。
影响我国的热带气旋源地：1. 菲律宾以东洋面；2. 关岛附近洋面；3. 南海中部洋面。
世界上受热带气旋影响最严重的国家：孟加拉湾、中 国、日本、东南亚、加勒比海地区和美国东部沿岸。 西北太平洋发生的热带气旋最多，约占北半球的66%。
3. 转向路径：先向西北后转向东北（个别登陆再入 海），从菲律宾以东向西北方向移动，到达我国东部 海面或沿海地区登陆，然后转向东北方向移去，路径 呈抛物线状。
在我国的登陆热带气旋，以温州到汕头一带为最多。
影响热带气旋移动的因子
1. 水平气压梯度力：热带气旋相对于东风带、西风带和副热带高压 等行星尺度系统来说，是一个较小的涡旋，作为质点，受气压梯度 力的影响。一般来说热带气旋移动方向与500百帕等压面上地转气流 一致。
降至最低
向中心升高,呈闷热 温度向中心逐渐升高
达最高，形成暖中心

2008年西北太平洋热带气旋的气候特征分析


２３ Ｔ ． Ｃ路 径特 点 而 ２０ 年 Ｔ ０ ８ Ｃ路 径分 布 为 ：西 行 有 ７ ，东 北 个
／一 。 ‘ 、
‘ 一 ｌ 一¨ Ｈ
，
行 ６ ，转 向 型 有 ５ ，西 北 行 有 ２个 ，北 上 ２ 个 个 个 。表 １ ２ ０ 年 西 北太 平洋 Ｔ 是 ０８ Ｃ路 径类 型 ，可 以 看 出 ２０ 年 Ｔ ０８ Ｃ路径 主要 以西行 、东北 行 和转 向型
料 以及 国家 气 候 中心 发 布 的 气候 再 分 析 资 料 ，分
析 西北 太平 洋 Ｔ Ｃ特 征 的成 因 ， 以期 对 相 似 年份 的 Ｔ 预 报提供 借鉴 。 Ｃ
２２ 发 生 期 早 、在 往 年 不 活跃 期 多发 而在 活 跃 季 ．
节 却偏 少 ，结束 期晚
２０ 年 Ｔ ０８ Ｃ的活 动 时 间集 中在 ４ １ ，其 中 ～ ２月
中图分 类 号 ： ４ ４ 文 献标 识 码 ： Ｐ４ Ａ 文章 编 号 ：０ ３０ ３ （ ０ ０ ０ ．０ ５０ １ ０ —２ ９ ２ １ ） ４０ ２ ．８
１ 引 言
西北 太平 洋是 世 界上 Ｔ Ｃ活动 最 为频 繁 的海 区，
２ ０ ８ 西北太平洋 Ｔ ２ ０ 年 Ｃ基本特征
候 平 均值 偏 强， 陆我 国的 比例偏 大 ，其 中有 １ 个 登 ４
Ｔ Ｃ对 西太 气 象组 织 １ 个 国家 和地 区造成 了较 大 的 ４
影 响 ，ｌ ３个 Ｔ Ｃ登 陆 ，其 中 朝 鲜 １ （ ８ ７ 海 个 ００ “
鸥 ” ，越南 ２ （ ８ ６ 米 克 拉 ” ８ １红 霞 ” ，菲 ） 个 ０ １“ 、０ ２ “ ）
路径 为 主 。其 中 ０ １ 号 Ｔ ８７ Ｃ西行 至南海 海域 转 为正 抛 物线 路 径 ，０１ ８ ９号 Ｔ Ｃ西 行 至 南 海 转 为 异 常
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

西北太平洋热带气旋摘要为减小气象灾害对我国造成的经济损失，文章中建立了预测模型对热带气旋的数目进行预测，利用SPSS软件对西北太平洋热带气旋基础信息要素进行相关性分析，并且重新调整热带气旋等级国家标准以更好的对热带气旋等级进行划分。

针对问题一，利用SPSS软件对西北太平洋热带气旋基础信息要素的数据进行归一化处理，将得到的数据进行相关性分析，由得到的相关系数可以看出：“平均速度”与“移动距离”、“寿命”、“维度幅度”的相关系数分别为0.295、-0.326、0.332，为弱相关关系，而“平均速度”与其余七个信息要素都不具有相关性；“维度幅度”与“经度幅度”也不具有相关性；其他信息要素之间的相关系数均大于或等于0.8，因此具有较强的相关性。

针对问题二，利用MATLAB绘制热带气旋发生频率的散点图，根据数值天气预报中的微扰动法，天气系统具有波动性，因此利用多个正弦函数之和来对散点图进行拟合，由拟合所得的曲线预测得到近年来西北太平洋热带气旋发生频率在升高，根据拟合所得的函数计算得2014年西北太平洋上会发生29个热带气旋。

针对问题三，热带气旋等级国家标准中各等级的气旋数目随时间波动变化，符合天气系统的发展规律，不做改正，根据2008、2009、2010年底层中心附近最大平均风速均大于或等于59.11米每秒，比往年超强台风都大，所以当底层中心附近最大平均风速大于或等于59.1米每秒时，划分出一个新等级，叫做甚强台风，当台风到达这个等级时，政府部门应发布更高级别的台风预警，以减小经济损失。

关键字：热带气旋相关性分析函数拟合热带气旋等级国家标准一、问题的重述西北太平洋热带气旋20世纪是人类历史上物质文明发展最快的世纪，科学技术取得了巨大的进展，数值天气预报的成功也重要展现了社会和科技的进步。

但是，经济越发展自然灾害造成的损失就越大，21世纪人类仍将面临频繁发生的自然灾害的威胁，热带气旋是世界上主要的自然灾害之一。

在我国, 气象灾害频数占整个自然灾害的70%以上，造成的经济损失占国内生产总值的3%-6%，这一比率比一般发达国家高,而台风灾害在气象灾害中占有相当一部分。

附录1给出了2000-2013年的西北太平洋热带气旋基础信息，附录2给出了2006年修订的热带气旋等级国家标准。

试利用附录1给出的2000-2013年的西北太平洋热带气旋基础信息分析如下问题：1）西北太平洋热带气旋基础信息要素之间相关吗？若相关，关系如何？2）近年来西北太平洋热带气旋发生频率在升高吗？2014年西北太平洋上会发生多少个热带气旋？3）2006年修订的热带气旋等级国家标准还合适吗？若不合适，你认为应该怎样调整？二、模型的假设1.附录中的数据真实有效；2.实际生活中没有突发情况的存在从而对模型预测的结果产生影响；3.各基础信息要素之间存在线性相关关系。

三、符号说明符号 含义 r相关系数t Pearson 简单相关系数的检验统计量 α显著性检验中给定的显著性水平y一年热带气旋发生个数四、问题的分析与求解问题一1.问题的分析与模型的建立客观事物之间的关系大致可归纳为两大类，即函数关系和统计关系。

而西北太平洋热带气旋基础信息要素之间相关关系在这里是统计关系。

统计关系可进一步划分为线性相关关系和非线性相关关系。

线性相关关系又可分为正线性相关关系和负线性相关关系。

正线性相关关系指两个变量线性的相随变动方向相同，而负线性相关关系指两个变量线性的相随变动方向相反。

事物之间的统计关系不像函数关系那样直接，但确实普遍存在，并且有的关系强，有的关系弱，程度各有差异。

通过对问题一要求的分析，我们决定对西北太平洋热带气旋基础信息要素之间相关关系进行线性相关分析。

由于这里的各要素都是定距型变量，我们利用Pearson 简单相关系数进行线性相关关系的评价，它的数学定义为：()()()()∑∑∑===----=ni ni iini iiy yx x y yx x r 11221 （1）式中，n 为样本量；i x 和i y 分别为两变量的变量值。

由式（1）可进一步计算简单相关系数，也即：⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=∑=y i n i x i S y y S x x n r 11 (2) 式（2）说明简单相关关系是n 个i x 和i y 分别标准化后的积的平均数。

于是可知简单相关系数有一下几个特点：● x 和y 在式（1）或式（2）中是对称的，说明x 与y 的相关系数等同于y 与x的相关系数。

● 由于相关系数是x 和y 标准化后的结果，因此简单相关系数是无量纲的。

● 对x 和y 作线性变换后可能会改变它们之间相关系数的符号（相关的方向），但不会改变相关系数的绝对值。

● 相关系数能够用于度量两变量之间的线性关系，但并不是度量非线性关系的有效工具。

Pearson 简单相关系数的检验统计量为t 统计量，其数学定义为：212rn r t --=(3)式中，t 统计量服从2-n 个自由度的t 分布。

2. 模型的求解由于SPSS 软件将自动计算Pearson 简单相关系数、t 检验统计量的观测值和对于的概率-P 值。

故只需将附录1中数据录入SPSS 软件中即可让SPSS 直接得出结果。

在得出结果的过程中为了计算的需要我们将寿命转化为小时数。

由于附录1中一些个案中暴风域最大半径和暴风域最大直径值缺失，于是在分析的过程我们分两种情况进行分析，一种是考虑暴风域最大半径和暴风域最大直径的情况下分析具有暴风域最大半径和暴风域最大直径值个案的各基础信息要素之间的相关关系；另一种是不考虑暴风域最大半径和暴风域最大直径的情况下分析全部个案的各基础信息要素之间的相关关系。

（1）考虑暴风域最大半径和暴风域最大直径利用SPSS 得到结果，结果如表1所示：表1 各要素相关关系表（1）最低气压最大风速强风域最大半径强风域最大直径移动距离 寿命 平均速度 纬度幅度 经度幅度暴风域最大半径暴风域最大直径最低气压Pearson Correlatio n1-0.968**-0.268** -0.328** -0.534** -0.578** 0.111-.0415** -0.371**-0.490** -0.561**Sig.(2-tailed) 0.000 0.000 0.000 0.000.000.1030.000.000.000 0.000最大风速PearsonCorrelation-0.968**1 0.181**0.240**0.520**0.570**-0.1130.395**0.361**0.411**0.483**Sig.(2-tailed)0.000 0.008 0.000 0.000.000.0980.000.000.000 0.000强风域最大半径PearsonCorrelation-0.268**0.181**1 0.957**0.391**0.289**0.0760.425**0.136*0.737**0.751**Sig.(2-tailed)0.000 0.008 0.000 0.000.000.2690.000.0460.000 0.000强风域最大直径PearsonCorrelation-0.328**0.240**0.957** 1 0.422**0.341**0.0370.419**0.182**0.758**0.793**Sig.(2-tailed)0.000 0.000 0.000 0.000.000.5920.000.0070.000 0.000移动距离PearsonCorrelation-0.534**0.520**0.391**0.422** 1 0.758**0.295**0.744**0.633**0.492**0.512**Sig.(2-tailed)0.000 0.000 0.000 0.000 0.000.000.000.000.000 0.000寿命PearsonCorrelation -0.578**0.570**0.289**0.341**0.758**1 -0.326**0.484**0.546**0.382**0.447**Sig.(2-tailed) 0.000 0.000 0.000 0.000 0.000.000.000.000.000 0.000平均速度PearsonCorrelation0.111 -0.1130.076 0.037 0.295**-0.326**1 0.332**0.1270.080 0.013Sig.(2-tailed)0.103 0.098 0.269 0.592 0.000.000.000.0640.246 0.855纬度幅度PearsonCorrelation-0.415**0.395**0.425**0.419**0.744**0.484**0.332**1 0.1040.500**0.473**Sig.(2-tailed)0.000 0.000 0.000 0.000 0.000.000.000.1290.000 0.000经度幅度PearsonCorrelation-0.371**0.361**0.136*0.182**0.633**0.546**0.1270.1041 0.251**0.287**Sig.(2-tailed)0.000 0.000 0.046 0.007 0.000.000.0640.1290.000 0.000我们可以从以下两个方面对表进行分析 1）相关系数r （表中Pearson 的值） 相关系数r 的取值在-1~1之间。

0>r 表示两变量存在正的线性相关关系；0<r 表示两变量存在负的线性相关关系。

1=r 表示两变量存在完全正相关关系；1-=r 表示两变量存在完全负相关关系，0=r 表示两变量不存在线性相关关系。

8.0>r 表示两变量之间具有较强的的线性相关关系；3.0<r 表示两变量之间的线性相关关系较弱。

2）检验统计量的概率-P （表中Sig.值）如果检验统计量的概率-P 值小于给定的显著水平α，则应拒绝原假设，认为两总体存在显著的线性关系；反之，如果检验统计量的概率-P 值大于给定的显著水平α，则不能拒绝原假设，认为两总体存在零相关。

基于以上两个方面，从表1中可以看出大部分基础信息要素之间存在线性相关关系，只是有强弱和正负的不同，但也有不存在线性相关关系的要素，如最低气压与很多要素都不存在相关关系。

但是在这种情况下，由于只对带有暴风域最大半径和暴风域最大直径值的个案进行了分析，而舍弃了没有这些值的个案，所以并不能完全揭示数据间隐藏的信息。

（2）不考虑暴风域最大半径和暴风域最大直径 利用SPSS 得到结果，结果如表2所示：暴风域最大半径Pearson Correlatio n -0.490**0.411**0.737** 0.758** 0.492**0.382**0.0800.500**0.251**1 0.945**Sig. (2-tailed).000 .000 .000 .000 .000 .000 .246 .000 .0000.000暴风域最大直径Pearson Correlatio n -0.561**0.483**0.751** 0.793** 0.512**0.447**0.0130.473**0.287**0.945**1Sig. (2-tailed)0.000 0.000 0.000 0.000 0.000.0000.8550.0000.0000.000**. Correlation is significant at the 0.01 level (2-tailed). *. Correlation is significant at the 0.05 level (2-tailed). a. Listwise N=215表2 各要素相关关系表（2）最低气压最大风速强风域最大半径强风域最大直径移动距离寿命平均速度纬度幅度经度幅度最低气压PearsonCorrelation 1 -0.978**-0.502**-0.549**-0.721**-0.753**0.067 -0.602**-0.571**Sig. (2-tailed) 0.000 0.000 0.000 0.000 0.000 0.230 0.000 0.000 N 326 326 326 326 326 326 325 325 325最大风速PearsonCorrelation -0.978**1 0.467**0.511**0.727**0.753**-0.045 0.600**0.586**Sig. (2-tailed) 0.000 0.000 0.000 0.000 0.000 0.414 0.000 0.000 N 326 326 326 326 326 326 325 325 325强风域最大半径PearsonCorrelation-0.502**0.467**1 0.965**0.559**0.493**0.073 0.568**0.340** Sig. (2-tailed) 0.000 0.000 0.000 0.000 0.000 0.192 0.000 0.000 N 326 326 326 326 326 326 325 325 325强风域最大直径PearsonCorrelation-0.549**0.511**0.965** 1 0.587**0.538**0.044 0.575**0.375** Sig. (2-tailed) 0.000 0.000 0.000 0.000 0.000 0.433 0.000 0.000 N 326 326 326 326 326 326 325 325 325移动距离PearsonCorrelation -0.721**0.727**0.559**0.587** 1 0.848**0.231**0.825**0.771**Sig. (2-tailed) 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 N 326 326 326 326 326 326 325 325 325寿命PearsonCorrelation -0.753**0.753**0.493**0.538**0.848**1 -0.213**0.656**0.682**Sig. (2-tailed) 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 N 326 326 326 326 326 326 325 325 325平均速度PearsonCorrelation 0.067 -0.045 0.073 0.044 0.231**-0.213**1 0.253**0.163**Sig. (2-tailed) 0.230 0.414 0.192 0.433 0.000 0.000 0.000 0.003 N 325 325 325 325 325 325 325 325 325纬度幅度PearsonCorrelation -0.602**0.600**0.568**0.575**0.825**0.656**0.253**1 0.380**Sig. (2-tailed) 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 N 325 325 325 325 325 325 325 325 325经度幅度PearsonCorrelation -.0571**0.586**0.340**0.375**0.771**0.682**0.163**0.380**1Sig. (2-tailed) 0.000 0.000 0.000 0.000 0.000 0.000 0.003 0.000N 325 325 325 325 325 325 325 325 325 **. Correlation is significant at the 0.01 level (2-tailed).分析方法如表1的分析方法。