离散傅里叶变换及其快速算法.

离散傅里叶变换及其快速算法离散傅里叶变换（Discrete Fourier Transform，DFT）是一种将离散信号转换为频域表示的数学工具。

它在信号处理、图像处理、通信等领域有广泛的应用。

而快速傅里叶变换（Fast Fourier Transform，FFT）是一种能够高效计算DFT的算法，大大减少了计算量。

首先，我们来看一下DFT的原理。

给定一个有限长度的离散信号序列x(n)，DFT将其转换为频谱X(k)，其中k为频率索引，取值范围为0到N-1，N为序列的长度。

DFT的定义公式如下：X(k) = Σ x(n) * exp(-j * 2π * nk / N)其中，exp为自然指数函数，j为虚数单位。

DFT将信号分解为了N个复数的和，这些复数代表了不同频率分量在信号中的贡献。

然而，直接计算DFT的时间复杂度非常高，为O(N^2)。

为了提高计算效率，Cooley和Tukey于1965年提出了FFT算法。

FFT算法基于以下性质：若N为2的整数次幂，则DFT可以被分解为两个较小长度的DFT的线性组合。

具体来说，将N个点的DFT拆分为长度为N/2的两个DFT，然后再对这两个子序列进行DFT，最后将两个子序列的结果组合起来。

这个过程可以递归地进行，直到序列长度为1，即可得到最终的DFT结果。

FFT算法的时间复杂度为O(NlogN)，远远小于直接计算DFT的复杂度。

这使得FFT成为了处理大规模数据的首选方法之一、此外，FFT还有其他一些优点，如可并行化计算、对称性质等。

FFT算法可以采用不同的实现方式，最著名的是基于蝶形运算的Cooley-Tukey算法。

这种实现方式将FFT过程分为了两个阶段：置换阶段和蝶形运算阶段。

置换阶段通过将信号重新排序，将原始序列分为奇偶两个子序列，并计算每个子序列的DFT。

这个过程可以递归地应用于子序列，直到长度为1蝶形运算阶段是FFT算法的核心部分。

蝶形运算是指将两个频域上的复数进行运算，得到新的复数。

实验四 离散傅里叶变换及其快速算法一、 实验目的掌握快速傅立叶变换的应用方法；二、 实验仪器：电脑一台，MATLAB6.5或更高级版本软件一套。

三、 实验原理和实例分析 （一）离散傅里叶变换离散傅立叶级数变换是周期序列，仍不便于计算机计算。

但离散傅立叶级数虽是周期序列，却只有N 个独立的数值，所以它的许多特性可以通过有限长序列延拓来得到。

对于一个长度为N 的有限长序列)(n x ，也即)(n x 只在)1(~0-=N n 个点上有非零值，其余皆为零，即⎩⎨⎧-≤≤=其他,010),()(N n n x n x把序列)(n x 以N 为周期进行周期延拓得到周期序列)(~n x ，则有：⎪⎩⎪⎨⎧-≤≤=其他,010),()(~N n n x n x所以，有限长序列)(n x 的离散傅立叶变换(DFT)为：10,)()]([)(10-≤≤==∑-=-N n W n x n x DFT k X N n knN逆变换为：10,)(1)]([)(10-≤≤==∑-=-N n W k X N k X IDFT n x N n kn N若将DFT 变换的定义写成矩阵形式，则得到： X=A ﹒x ，其中DFT 变换矩阵A 为⎪⎪⎩⎪⎪⎨⎧=---2)1(111...1...............11...11N NN N N N N W W W W ADftmtx 函数：用来计算DFT 变换矩阵A 的函数A ＝dftmta （n ）：返回n ×n 的DFT 变换矩阵A 。

若x 为给定长度的行向量，则y ＝x*A ，返回x 的DFT 变换y 。

Ai ＝conj （dftmtx （n ））/n ；返回n ×n 的IDFT 变换矩阵Ai 。

【实例4-1】 >> A=dftmtx(4) >> Ai=conj(dftmtx(4))/4 运行结果A =1.0000 1.0000 1.0000 1.0000 1.0000 0 - 1.0000i -1.0000 0 + 1.0000i1.0000 -1.0000 1.0000 -1.0000 1.0000 0 + 1.0000i -1.0000 0 - 1.0000i Ai =0.2500 0.2500 0.2500 0.2500 0.2500 0 + 0.2500i -0.2500 0 - 0.2500i0.2500 -0.2500 0.2500 -0.2500 0.2500 0 - 0.2500i -0.2500 0 + 0.2500i【实例4-2】如果)4/sin()8/sin()(ππn n n x +=是一个N ＝16的有限序列，用MATLAB 求其DFT 的结果，并画出其结果图，如图4－1所示。

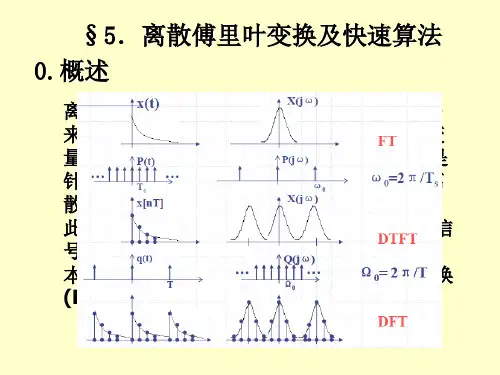
第五章 离散傅里叶变换及其快速算法 1 离散傅里叶变换(DFT)的推导(1) 时域抽样：目的：解决信号的离散化问题。

效果：连续信号离散化使得信号的频谱被周期延拓。

(2) 时域截断：原因：工程上无法处理时间无限信号。

方法：通过窗函数(一般用矩形窗)对信号进行逐段截取。

结果：时域乘以矩形脉冲信号，频域相当于和抽样函数卷积。

(3) 时域周期延拓：目的：要使频率离散，就要使时域变成周期信号。

方法：周期延拓中的搬移通过与)(s nT t -δ的卷积来实现。

表示：延拓后的波形在数学上可表示为原始波形与冲激串序列的卷积。

结果：周期延拓后的周期函数具有离散谱。

(4)1。

图1 DFT 推导过程示意图(5) 处理后信号的连续时间傅里叶变换：∑∑∞-∞=-=π--δ⋅⎥⎥⎦⎤⎢⎢⎣⎡=k N n N kn j s kf f e nT h f H )()()(~010/2(i))(~f H 是离散函数，仅在离散频率点SNT kT k kf f ===00处存在冲激，强度为k a ，其余各点为0。

(ii) )(~f H 是周期函数，周期为ss T NT N T N Nf 100===，每个周期内有N 个不同的幅值。

(iii) 时域的离散时间间隔(或周期)与频域的周期(或离散间隔)互为倒数。

2 DFT 及IDFT 的定义(1) DFT 定义：设()s nT h 是连续函数)(t h 的N 个抽样值1,,1,0-=N n ，这N 个点的宽度为N 的DFT 为：[])1,...,1,0(,)()(10/2-=⎪⎪⎭⎫⎝⎛==∆-=π-∑N k NTk H enT h nT h DFT s N n Nnk j s s N (2) IDFT 定义：设⎪⎪⎭⎫⎝⎛s NT kH 是连续频率函数)(f H 的N 个抽样值1,,1,0-=N k ， 这N 个点的宽度为N 的IDFT 为：())1,...,1,0(,110/21-==⎪⎪⎭⎫ ⎝⎛=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫⎝⎛∆-=π--∑N k nT h e NTkH NNT kH DFT s N k N nk j s sN (3) N nk j e /2π-称为N 点DFT 的变换核函数，N nk j e /2π称为N 点IDFT 的变换核函数。