材料力学——第12章(压杆稳定计算)
- 格式:pdf
- 大小:3.84 MB
- 文档页数:65
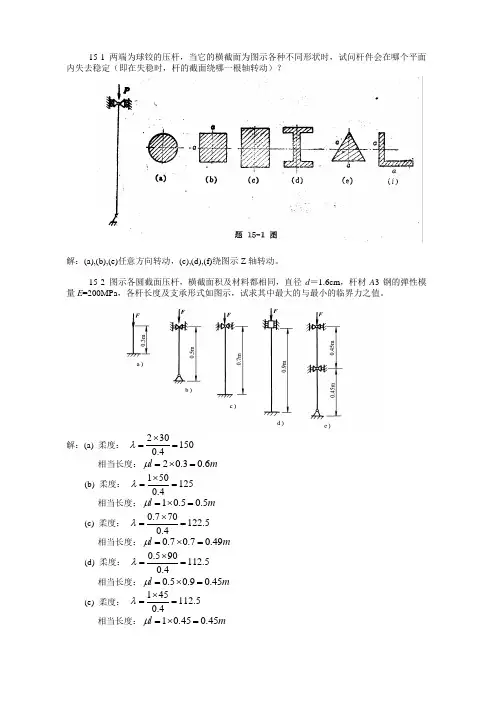
15-1 两端为球铰的压杆,当它的横截面为图示各种不同形状时,试问杆件会在哪个平面内失去稳定(即在失稳时,杆的截面绕哪一根轴转动)?解:(a),(b),(e)任意方向转动,(c),(d),(f)绕图示Z 轴转动。
15-2 图示各圆截面压杆,横截面积及材料都相同,直径d =1.6cm ,杆材A 3钢的弹性模量E =200MPa ,各杆长度及支承形式如图示,试求其中最大的与最小的临界力之值。
解:(a) 柔度: 2301500.4λ⨯== 相当长度:20.30.6l m μ=⨯=(b) 柔度: 1501250.4λ⨯== 相当长度:10.50.5l m μ=⨯=(c) 柔度: 0.770122.50.4λ⨯== 相当长度:0.70.70.49l m μ=⨯=(d) 柔度: 0.590112.50.4λ⨯== 相当长度:0.50.90.45l m μ=⨯=(e) 柔度: 145112.50.4λ⨯== 相当长度:10.450.45l m μ=⨯=由E=200Gpa 及各柔度值看出:各压杆的临界力可用欧拉公式计算。
即:()22cr EIF l πμ=各压杆的EJ 均相同,故相当长度最大的压杆(a)临界力最小,压杆(d)与(e)的临界力最大,分别为:()2948222320010 1.610640.617.6410cr EFF l N πππμ-⨯⨯⨯⨯⨯===⨯()2948222320010 1.610640.4531.3010cr EIF l Nπππμ-⨯⨯⨯⨯⨯===⨯15-3 某种钢材P σ=230MPa ,s σ=274MPa ,E =200GPa ,直线公式λσ22.1338-=cr ,试计算该材料压杆的P λ及S λ值,并绘制1500≤≤λ范围内的临界应力总图。
解:92.633827452.5p s s a λπσλ===--===15-4 6120型柴油机挺杆为45钢制成的空心圆截面杆,其外径和内径分别为,12mm 和10mm ,杆长为383mm ,两端为铰支座,材料的E =210GPa ,P σ=288MPa ,试求此挺杆的临界力cr F 。

材料力学压杆稳定概念欧拉公式计算临界力材料力学是研究物体受力及变形行为的一门学科。
压杆稳定是材料力学中重要的概念之一、当一个杆件受到作用力时,如果杆件不发生任何形状上的变化,我们称之为杆件处于稳定状态。
然而,当作用力超过一定临界值时,杆件就会发生失稳,产生形状上的变化。
因此,欧拉公式就是用来计算杆件临界力的一种方式。
欧拉公式由瑞士数学家欧拉于18世纪中叶首次提出。
它的基本假设是杆件是理想化的,即杆件是均匀、无缺陷、具有均匀截面的杆件。
根据欧拉公式,杆件临界力可通过以下公式计算:Pcr = (π^2 * E * I) / L^2其中,Pcr表示临界力,E表示杨氏模量,I表示截面惯性矩,L表示杆件的有效长度。
从上述公式中可以看出,临界力与材料的弹性模量有关,即材料越硬,临界力越大;同时临界力与截面的形状也有关,即截面惯性矩越大,临界力越大;临界力还与杆件长度有关,即杆件越短,临界力越大。
例子:假设有一根长为L的无缺陷的圆柱形杆件,其截面半径为r,杨氏模量为E。
根据材料力学的知识,该圆柱形杆件的截面惯性矩可计算为I=(π*r^4)/4Pcr = (π^2 * E * ((π * r^4) / 4) ) / L^2通过上述公式,可以计算出该无缺陷的圆柱形杆件的临界力。
这个临界力表示了该杆件能够承受的最大作用力。
如果作用力超过了临界力,该杆件将发生失稳,产生形状上的变化。
总结起来,材料力学中的压杆稳定概念是指杆件在受力作用下不发生形状上的变化。
欧拉公式是用来计算杆件临界力的一种常用公式,可以帮助工程师们确定杆件的最大承载能力。




材料力学习题第12章12-1一桅杆起重机,起重杆AB的横截面积如图所示。
钢丝绳的横截面面积为10mm2。
起重杆与钢丝的许用σ,试校核二者的强度。
力均为MPa[=]12012-2重物F=130kN悬挂在由两根圆杆组成的吊架上。
AC是钢杆,直径d1=30mm,许用应力[σ]st=160MPa。
BC是铝杆,直径d2= 40mm, 许用应力[σ]al= 60MPa。
已知ABC为正三角形,试校核吊架的强度。
12-3图示结构中,钢索BC由一组直径d =2mm的钢丝组成。
若钢丝的许用应力[σ]=160MPa,横梁AC单位长度上受均匀分布载荷q =30kN/m作用,试求所需钢丝的根数n。
若将AC改用由两根等边角钢形成的组合杆,角钢的许用应力为[σ] =160MPa,试选定所需角钢的型号。
12-4图示结构中AC为钢杆,横截面面积A1=2cm2;BC杆为铜杆,横截面面积A2=3cm2。
[σ]st = 160MPa,[σ]cop [F。
= 100MPa,试求许用载荷]12-5图示结构,杆AB为5号槽钢,许用应力[σ] = 160MPa,杆BC为bh= 2的矩形截面木杆,其截面尺寸为b = 5cm, h = 10cm,许用应力[σ] = 8MPa,承受载荷F = 128kN,试求:(1)校核结构强度;(2)若要求两杆的应力同时达到各自的许用应力,两杆的截面应取多大?12-6图示螺栓,拧紧时产生∆l = 0.10mm的轴向变形,试求预紧力F,并校核螺栓强度。
已知d1=8mm, d2=6.8mm, d3=7mm, l1=6mm, l2=29mm, l3=8mm; E=210GPa, [σ]=500MPa。
12-7图示传动轴的转速为n=500r/min,主动轮1输入功率P1=368kW,从动轮2和3分别输出功率P2=147kW 和P3=221kW。
已知[σ]=212MPa,[ ϕ]=1︒/m, G =80GPa。
(1)试按第四强度理论和刚度条件确定AB段的直径d1和BC段的直径d2。




材料力学压杆稳定公式材料力学是物理学的一个分支,研究物质的力学性质和物理性质以及它们之间的相互作用。
材料力学中的压杆稳定性问题,在工程中应用非常广泛,是一种典型的应用力学问题。
本文将对压杆稳定公式进行详细解析,并探讨它在实际应用场景中的应用。
一、压杆稳定公式的原理当压力作用于杆的轴向时,可能会导致杆件翻转或折断,这种失稳现象称为压杆稳定性。
压杆稳定性是压力元素设计过程中必须考虑的关键问题。
压杆稳定公式是工程师计算杆件失稳情况的重要工具。
压杆稳定公式由欧拉公式和Johnson公式组成。
欧拉公式是描述简单结构(如棒杆)失稳所必需满足的基本条件,它给出了压杆稳定的临界条件。
欧拉公式的表达式为:Pcr = π²EI/l²Pcr为极限荷载(稳定负荷),E为杨氏模量,I为惯性矩,l为杆的长度。
Johnson公式是实际应用中采用的压杆稳定公式,它考虑了杆的附加载荷和杆的弯曲刚度对稳定性的影响。
Johnson公式的表达式为:Pcr= σcA/{1+(σs/σc)[(A/A0)^2-1]}Pcr为极限荷载,σc为杆的材料弹性极限,σs为附加载荷产生的应力,A为杆的横截面积,A0为杆的理论横截面积。
Johnson公式是以欧拉公式为基础的,可以用于计算矩形截面、圆形截面和其他截面形状的杆件的极限稳定荷载。
二、压杆稳定公式的实际应用场景1.结构设计压杆稳定公式在结构设计中是至关重要的。
当设计师有多种杆件形状和材质可供选择时,可以利用压杆稳定公式计算每种形状和材质的极限荷载,以找到最适合的材质和形状。
2.建筑施工压杆稳定公式在建筑施工中也有广泛的应用。
在桥梁、塔和钢构建筑的建设中,压杆稳定公式可以帮助工程师确定结构的稳定性。
它们还可以检查杆件的尺寸和重量是否适当。
3.飞机制造在飞机制造中,压杆稳定公式可以用来计算气动稳定性问题,以确保飞机在不同高度和气压下的稳定性。
这对于飞行安全至关重要。
4.交通工程压杆稳定公式在交通工程中也有广泛应用。
