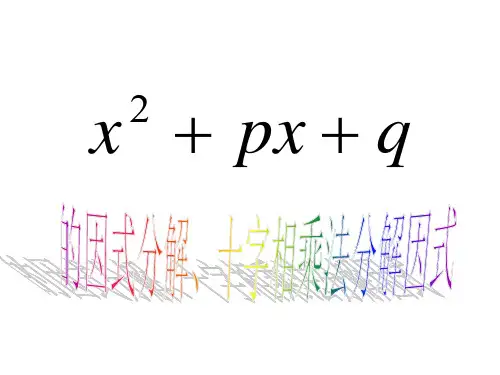当前位置：文档之家 › 人教版《因式分解》优秀课件ppt1

人教版《因式分解》优秀课件ppt1

  • 格式：ppt
  • 大小：154.50 KB
  • 文档页数：28

下载文档原格式

  / 28

合集下载

人教版教材《因式分解》ppt1

人教版教材《因式分解》ppt1
pq
人教版八年级上册数学14.3因式分解 十字相乘法分解因式 课件
人教版八年级上册数学14.3因式分解 十字相乘法分解因式 课件
十字相乘法（借助十字交叉线分解因式的方法）
例一：
步骤：
x2 6x 7 (x 7)(x 1) ①竖分二次项与常数项
x
7 7
或
x 1 1
②交叉相乘，和相加 ③检验确定，横写因式 顺口溜：竖分常数交叉验，
6
－5
2
－1
－1－10=－11
1
1
－5＋6=1
人教版八年级上册数学14.3因式分解 十字相乘法分解因式 课件
人教版八年级上册数学14.3因式分解 十字相乘法分解因式 课件
练习：将下列各式分解因式 1、 7x 2－13x＋6 答案(7x-6)(x-1) 2、 －y 2－4y＋12 答案－ (y＋6)(y－2) 3、 15x2＋7xy－4y 2 答案 (3x－y)(5x＋4y) 4、 x 2－(a＋1) x＋a 答案 (x－1)(x－a)
人教版八年级上册数学14.3因式分解 十字相乘法分解因式 课件
练一练： 将下列各式分解因式
1x2 5x 6 3x2 7x 12
2x2 x 6 4x2 3x 10
x2
小结：用十字相乘法把形如
px q 二次三项式分解因式
q ab, p a b
当q>0时，q分解的因数a、b( 同号 )
人教版八年级上册数学14.3因式分解 十字相乘法分解因式 课件
人教版八年级上册数学14.3因式分解 十字相乘法分解因式 课件
你能对下列式子进行分解因式吗？
x y2 8x y 48
人教版八年级上册数学14.3因式分解 十字相乘法分解因式 课件

人教版九年级上册因式分解法课件(1)

人教版九年级上册因式分解法课件(1)

(1)x2-4=0;
(2)(x+1)2-25=0.
解：(x+2)(x-2)=0, 解：[(x+1)+5][(x+1)-5]=0,
∴x+2=0或x-2=0. ∴x1=-2, x2=2.
∴x+6=0或x-4=0. ∴x1=-6, x2=4.
提升练习
用分解因式法解下列方程：
5x2 2x 1 x2 2x 3
当一元二次方程的一边是0,而另一边易于分解成两个一次因式 的乘积时,我们就可以用分解因式的方法求解.这种用分解因式解 一元二次方程的方法称为分解因式法.
1.用分解因式法的条件是:方程左边易于分解,而右边等于零. 2.理论根据是“如果两个因式的积等于零,那么至少有一个因 式等于零.”
例题分析
例 用分解因式法解方程:
x1=0或x2=9
小亮的解法：
解：设这个数为x
x2=9 x
约去x得
x=9
他们做得是否 正确，若是错 了,错在哪里, 给与改正
(2)2x(2x-1) 3(2x 1) 0 解：(2x 1)(2x 3) 0
5x 0或3x 2 0
x1
0，x2
2 3
2x 1 0或2x 3 0
x1
1 2
，x2
3 2
当堂检测
6.一个数的平方与这个数的9倍相等这个数是几？
下面是明明,小亮解题过程
明明的解法： 解：设这个数为x
x2=9x x2-9x=0 x(x-9)=0 x=0或x-9=0
第21章 一元二次方程
21.2.3 一元二次方程的解法---因式分解法
人教版 九年级上册
学习目标
1.了解因式分解法解一元二次方程的概念，并会用分解因式 法解某些一元二次方程.

课件《因式分解》课件PPT_人教版1

课件《因式分解》课件PPT_人教版1

x=
（b2-4ac≥0）
( x －4 ) 2 － ( 5 － 2x )2=0.
5 ， x2=5.
导入新知
1. 解一元二次方程的方法有哪些？
直接开平方法 x2=a (a≥0)
配方法
(x+m)2=n (n≥0)
公式法
x= b b2 4ac（b2-4ac≥0）
2a
2. 什么叫因式分解?
把一个多项式分解成几个整式乘积的形式叫做因式 分解，也叫把这个多项式分解因式.
(4)移项，得 y2－2y－15＝0.
a b c (∵2ax＝∵＋31，)(b2＝＝x－－314，，)=c0＝. －＝1，－4， ＝－1，
②(x－1)2＝3；
把方程左边因式分解，
y y x①b=2x－∴2－4ax3c＝x=＋(－1－＝100)；－（2－b240-=41±a0c0≥0）－24×2－3 4×3×－1＝2±3
能力提升题
我们已经学习了一元二次方程的四种解法：直 接开平方法、配方法、公式法和因式分解法．请从 以下一元二次方程中任选一个，并选择你认为适当 的方法解这个方程．
降次，化为两个一次方程
x 0 或 10 4.9x 0
解两个一次方程，得出原方程的根
x1 0,
100 x2 49 2.04
这种解法是不是很简单？
探究新知
【思考】以上解方程 10x-4.9x2=0 的方法是如何使二次方 程降为一次的？
x(10-4.9x)=0 ①
x=0或10-4.9x=0 ②
（2）x(x+4)=8x+12. 解：x2-4x-12=0，
(x+1)2=-1.
(x-2)2=16.
此方程无解.
x1=6, x2=-2.

人教版九年级数学上册因式分解法课件(1)

人教版九年级数学上册因式分解法课件(1)

活动
什么时候可以用因式分解法？
当一元二次方程的一边是0,而另一边易于分解成两个一次因式的乘 积时,我们就可以用分解因式的方法求解.这种用分解因式解一元二 次方程的方法称为分解因式法.
使用因式分解法的条件
1.用分解因式法的条件是:方程左边易于分解,而右边等于零; 2.关键是熟练掌握因式分解的知识; 3.理论仍旧是“如果两个因式的积等于零,那么至少有一个因式等于
零.”
分解因式法解一元二次方程的步骤
1. 化方程为一般情势; 2. 将方程左边因式分解; 3. 根据“至少有一个因式为零”,转化为两个一元一次方程. 4. 分别解两个一元一次方程，它们的根就是原方程的根.
例题
解方程： 1. x2－3x＋2＝0.
2. x2－5x－6＝0.
3. x2－10x＋9＝0.
练习
解一元二次方程x2＋2x－3＝0时，可转化为两个一元一次方程，请 写出其中一个一元一次方程
选择合适的方法解一元二次方程
1. 配方法解一元二次方程要先配方，再降次； 2. 通过配方法可以推导求根公式，直接利用求根公式可以求出一
元二次方程的两根； 3. 用因式分解法要先使方程一边化为两个一次因式相乘的情势，
21.2.3因式分解法
复习
1. 我们已经学过了几种解一元二次方程的方法?
2. 什么叫因式分解? 若ab＝0，则a＝0或b＝0；若(x－a)(x－b)＝0，则方程的根为x1＝a， x2＝b
用因式分解法解形如x2＋bx＝0的一元二次方程
形如x2＋bx＝0的方程，可以用提取公因式法将方程的左边分解成 x(x＋b)的情势，从而将原方程转化为x(x＋b)＝0，这样可得原方程 的解为x1＝0，x2＝－b.
另一边为0，再分别使每个一次因式等于0. 4. 配方法、公式法适用于解所有有实数根的一元二次方程；因式

课件《因式分解》精品ppt课件_人教版1

课件《因式分解》精品ppt课件_人教版1

构造平方差形式
[4x (x2 4)][4x (x2 4)] 运用平方差公式
(4x x2 4)(4x x2 4) 去掉多重括号 (x2 4x 4)(x2 4x 4) 整理、提出负号
a2 2ab b2 a2 2ab b2 (a b)2 (a b)2
二、例题解析 （1)
x2 32 a2 b2 (a b)(a b)
二、例题解析
例 分解因式：
解： (1) 2x2 18 2(x2 9)
确定公因式“2” 将公因式“2”提出
2(x 3)(x 3)； 再用平方差公式分解
二、例题解析 例 分解因式：
解：(2)256m4 81n4 (16m2 )2 (9n2 )2
关键是找准各项的公因式
4.因式分解的基本方法---公式法
因式分解的概念
提公因式法
因式分解的基本方法
平方差公式
公式法
完全平方公式
（1）我们学过了哪些因式分解的公式？
4.因式分解的基本方法---公式法
因式分解的概念 因式分解的基本方法
提公因式法 公式法
（2）平方差公式的结构特征. a(a2 b)2(a (ab) b)a(a2 b)2
平方差公式 完全平方公式
4.因式分解的基本方法---公式法
因式分解的概念 因式分解的基本方法
提公因式法 公式法
（3）完全平方公式的结构特征. a(a2 b2)a2bab22 2(aabbb)2
平方差公式 完全平方公式
当
，时
同底数幂除法的运算性质
因式分解的一般步骤及注意事项
（4) （3)
5.
因式. 分解的一般步骤 ；
[(x2 1) 2x]2
运用完全平方差公式

因式分解ppt(共22张PPT)

因式分解ppt(共22张PPT)
3．（随堂练习p3１、２）
规律总结
• 对多项式分解因式与整式乘法是方向相反的两种恒等变 形.
• 整式的乘法运算是把几个整式的积变为多项式的形式，
特征是向着积化和差的形式发展；
• 多项式的分解因式是把一个多项式化为几个整式乘积的
形式，特征是向着和差化积的形式发展.
• 因式分解要注意以下几点: 1.分解的对象必须是多项式.
• 把一个多项式化成几个整式的积的形式,这 种变形叫做因式分解。
• 因式分解也可称为分解因式。
因分解的结果要以积的形式表示
2.每个因式必须是整式，且每个因式的次数 都要低于原多项式的次数。
3.必须分解到每个多项式不能分解为止（具 体由所在的数集决定）。
想一想: 因式分解与整式乘法有什么联系?
2.分解的结果一定是几个整式的乘积的形式.
2：计算
(1) 8728713 (2) 1012992
=87（87+13） =8700
=(101+99)(101-99) =200×2 =400
3.若 x101,y99则 x22xyy2_ 4_
动脑筋
n2+n是奇数还是偶数？
2517－532能被120整除吗? 若n是整数,证明 (2n+1)2-(2n-1)2是8的倍数.
多项式的因式分解与整式乘法是方向相反的恒等式.
整式乘法
3x(x-1)= _____
(3).(5a-1) =25a -10a+1 解: ab-ac=a(b-c)
a(a+1)(a-1) a3-a=a(a+1)(a-1)
2
2
整式乘法
答: 由a(a+1)(a-1)得到a3-a的变形是整式乘法，由a3-a得到a(a+1)(a-1)的变形是把一个多项式化成几个整式的积的形式.

人教版《因式分解》课件PPT人教版1

人教版《因式分解》课件PPT人教版1

= ( x+y ) ( x –y ) –2 ( x–y )
(m+1 – 2n) (m–1 + 2n)
= ( x–y ) ( x+y–2 )
(a + b) (ab – 1)
(a – b+1) (a – b – 1)
A知．识–点3x2y：2 因式分解B的．方–2法x2与y2步骤 （3五））-x利2+用4x分y-4组y2分解法分解因式
(2)x2－6x＋8＝__(_x_－__4_)_(_x_－__2_)______；
(3)a2＋8a＋12＝___(a_＋__2__)(_a_＋__6_)______; (4)x2－x－6＝ ___(x_－__3_)_(_x_＋__2_)______; (5)2x2＋5x－3＝___(2_x_－___1_)(_x_＋__3_)_____ ． (6)x2－5xy＋6y2＝ __(x_－__2_y_)_(_x_－__3_y_)_____．
?
?
x
+3
?
?
? + ? =?
2x +1 +6x +x =+7x
【例5】多项式 2x2+7x+3如何利用十字相乘进行因式分解？
?
?
x
+3
?
?
? + ? =?
2x +1 +6x +x =+7x
知识点2 ：因式分解的方法与步骤
跟踪练习
(1)x2＋4x＋3＝__(x_＋__3_)_(_x_＋__1_)______；
2.（2020•广东11/25）分解因式：xy-x=___x_(_y_-_1_) _____.

因式分解_ppt1

因式分解_ppt1

x
3
x -7
x -3
x5
因式分解_ppt1
计算：(x+2)(3x+5) =3x2+11x+10 反过来：3x2+11x+10 =(x+2)(3x+5) 我们可以发现，二次项3x2分解成 x、3x 的积； 常数项10分解成 2、5 的积；
x
2
x ·5＋2 ·3x = 11x
3x
5
这个例子启发我们，如何把二次三项式
ax2+bx+c进行分解
因式分解_ppt1
因式分解_ppt1
例2、把下列各式分解因式：
（1）2x 2-7x+3
（2）6x 2-7x-5
（3）5x 2+6xy-8y2 （4）ab2+4abc+3ac 2
解：（1）原式=（x-3)(2x-1）
x
-3
2x -1
（2）原式=（2x+1)(3x-5）
2x 1 3x -5
因式分解_ppt1
x2 px q
因式分解_ppt1
1、(x+3)(x-4) =x2-x-12 2、(a-6)(a-5)=a2-11a+30 3、(y+1)(y-3) =y2-2y-3
(x a)(x b) x2 (a b)x ab
能分解x 2 5x 6吗？
(x a)(x b) x2 (a b)x ab
x2 x2 5x 6 (2) a2 2a 3 (3) x2 2x 8 (4) (x y)2 3(x y) 2
x 2 px q 分解方法
(1)找出a，b使a+b=p且ab=q (先分解q再考虑p)
(2)把q分解成两个整数的积的符号规律： q＞0则a，b同号， 若p＞0，a，b同正，若p＜0，a，b同负； q＜0则a，b异号， 若p＞0，a，b中正数绝对值大， 若p＜0，a，b中负数的绝对值大。

初中数学人教版《因式分解》PPT经典课件1

初中数学人教版《因式分解》PPT经典课件1

(2) (a b ) 4a b ; B．可以变形为4m2-1 (2m)2-12 符合；
2
22
多项式4y2+my+9是完全平方式，其中含有哪两项平方，并且符号相同呢
22
C．也可以变形为y2-36x2，符合；
若是三项多项式，可以考虑是否使用完全平方公式；
此多项式能用公式法分解因式吗
这个三项多项式符合完全平方公式吗
可以使用什么方法分 解
注：确定公因式，首先观察系数的最大公约数，再观察 相同字母，及相同字母的最小指数.
例 分解下列因式
(2) 4xy2 4x2 y y3
解: 4xy2 4x2 y y3
y(4xy 4x2 y2 )
提 4吗xy取-4公多母x首2因-项的y项式2式降,可含y按幂后以有某排，再负个列剩继号字，余续, 因分式解 应先提取负号,
总结与回顾： BD．．可-m以2-变1=形-(m为24+m12)，-1不符(2合m．)2故-12选择D符．合；
因式分解的结果中,若有相同因式,应写成幂的形式.
1.多项式分解因式的一般方法与步骤； A． a2-( 4b)2 符合；
提取公因式后剩余多项式可以再分解吗 相同字母，及相同字母的最小指数.
2.多项式分解因式结果的一般要求． 多项式分解因式要分解到每个因式不能再分为止.
A.x2 1 B. x2 2x 1 C. x2 4x 4 D. x2 x 1
分析(1)审题:能用完全平方公式；
(2)判断:
选择C
从项数入手，排除A；
从符号入手，排除B； x2 4x 4 x2 2 2x 22.
从公式结构入手，排除D； x2+4x+4=(x+2)2
例 将多项式x3-xy2分解因式，结果正确的是
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

◆不论a、b为何数，代数式 a2+b2-2a+4b+5的值总是 （ D ） A.0 B.负数 C.正数 D.非负数
若n是任意正整数.试说明 3n+2-4×3n+1+10×3n能被7 整除.
思维再现
◆多项式9x2+1加上一个单项式后,使 它能成为一个整式的平方,则加上的单 项式可以是
_±__6_x__、_-_9_x_2__、__-_1_、__84_1_x_4(填上你认为
例4. 用简便方法计算：
(1)88281122 (2)19929399189918992 8
例5. 计算：
(1)x3y2z2 x3y2z2 (2)2a3b2 22a3b2a5b2a5b2
(3)当a3时,求代数式
a12a1a3a13a2a1的值 .
例6.
(1)已知 x 2 y 3 0, 试求值： x 2 4 y 2 4 xy 3 x 6 y 8 . ( 2 )已知 x y 2 a , y z 2 a , 且 a 2 7 , 试求 x 2 y 2 z 2 xy yz zx 的值 . (3)若 4 a 2 4 a b 2 6b 10 0, 则 a 3b b 3a的值是多少 ? ( 4 )已知 x 2 y 2 10 xy y 2 4 y 29 0 , 求 x 2 y 2 2 x 3 y 2 x 4 y 2的值 .
式：
sp (p a )(p b )(p c )(其 中 p a 2 b c ) ②
正确的一个即可,不必考虑所有的可能 情况).
例1. 对下列多项式因式分解：
(1) 2 x 2 y 2 4 y 3 z ( 2 ) 1 x 3 2 xy 2
2
( 3 )16 x 2 x 2 4 2
( 4 ) 25 x 2 20 xy 4 y 2 ( 5 ) a 2 b 2 10 ab 25
《 因 式 分 解 》优秀 课件pp t1 《 因 式 分 解 》优秀 课件pp t1
三大方法四项注意
提公因式法； 平方差公式； 完全平方公式；
三大方法四项注意
⑴有公因式的先提公因式； ⑵括号内要合并同类项； ⑶括号内首项系数要为正； ⑷括号内不能再分解；
力挽狂澜
x2y－4xy＋4y
1 a 4 27 3
(3)若 2 64 1可以被 60 至 70 之间的两个整数整除， 试求这两个数 . (4)两个奇数的平方差能被 8整除吗？为什么？
例8.
已知对多2项 x3式 x213xk进行因式分 有一个因2式 x3是 ,试求 4k24k1的值 .
1.下列变形中，从左边到右边是分解因式的是( )
A.mx+nx-n=(m+n)x-n
例7.
(1)已知 a 、 b 、 c是 ABC 的三边长，
则代数式 a 2 2 ab b 2 c 2的值
( A)大于零 ( B )等于零 (C )小于零 ( D )不能确定 ( 2 )已知 x 2 xy 12 , 且 xy y 2 13 ,
求 x y 2 和 x 2 y 2的值 .
项式4x 3 xy 2 ，若x=10,y=10则用上述方法
产生的密码是：___________
【例3】 .我国古代数学家秦九韶在《数书九章》 中记述了“三斜求积木”即已知三角形的三边长， 求它的面积。用现代式子表示即为：
s 1 4[a2b2(a2b 22c2)2]
①
而另一个文明古国希腊也有求三角形面积的海伦公
代数式是( )
A.3xm
B.3xm -1
C.xm-3
D.3x2m-1
6. 为使x2-6x+b在整数范围内可以分解因式，则
b可能取的值为
. （任写一个）
7.计算 1 2 4 2 2 5 2 5 7 6 2______
8.计算 1 2 2 2 + 2 2 3 2 +…+ 9 9 2 1 0 0 2 = ___________
B.21x3y2=3x3·7y2
C.4x2-9=(2x+3)(2x-3)
D.(3x+2)(x-1)=3x2-x-2
2.分解因式：x2-x=
.
3.下列各式中能用平方差公式分解因式的是( )
A.4x2+y2
B.-x2-25y2
C.(x-2y)2-9
D.x6-y3
4.分解因式：x2-4x+4=
.
5.用提公因式法把 9x2m3xm 分解因式后，括号内的
1 2 2 3
99 100
9.若a,b,c为△ABC的三边,
试判断代数式 a2(b22bcc2) ___ 0
10.若a,b,c为△ABC的三边，且满足
a2b2c2abbcac，请判断△ABC的形状为_____
➢ 典型例题解析
【例1】 因式分解： (1)-4x2y+2xy2-12xy； (2)9(x+y)2-4(x-y)2； (3)(x2+2x)2+2(x2+2x)+1； (4)(a2+b2)2-4a2b2.
例2. 把下列多项式因式分解：
(1)a 2 a b a b (2)a b2 2a b 1Biblioteka (3) x 4 16 y 4
(4)x 1x 3 1
(5)18 a 4 x 2 24 a 2 x 2 y 8 x 2 y 2
例3. 把下列多项式因式分解：
(1) x 2 x 12 (2)3 x 2 15 x 18 (3)ab a b 1
(x2－5)2＋2(x2－5)＋1 81a4－72a2b2＋16b4
(x2+y2)(x2+y2-4)+4
试说明：任意四个连续整数的积 与１的和是一个完全平方数．
若9x2＋2(a－4)x＋16是
一个完全平方式,则a的值
是
.
智力测试
甲、乙两同学分解因式x2+ax+b 时，甲看错了b，分解结果是 (x+2)(x+6),乙看错了a，分解结 果是(x+1)(x+16).请你分析一下a、 b的值分别为多少，并写出正确 的分解过程.
【例2】在日常生活中如取款，上网等需要密码，
有一种“因式分解”法产生的密码,方便记忆。原
理是：如对于多项式 x 4 y因4 式分解的结果
是 (xy)(xy)(x2y2 )，若取X=9,y=9时，
则各因式的值是x-y=0,x+y=18, x 2 y 2 =162,
于是就可以把018162作为一个六位密码，对于多