下载文档原格式
正弦稳态电路的分析1.复数法分析：a. 复数电压和电流表示：将正弦波电流和电压表示为复数形式，即I = Im * exp(jωt)，V = Vm * exp(jωt)，其中Im和Vm为幅值，ω为角频率，j为虚数单位。
b.使用欧姆定律和基尔霍夫定律来建立复数表达式。
c.找到电路中的频域参数，如电阻、电感和电容等，并使用复数法计算电路中的电流和电压。
d.计算电源电压和电流的相位差，这会决定电路中的功率因数。
2.相量法分析：a.相量表示：将电路中的电流和电压表示为相量形式，即以幅值和相位角表示，例如I=Im∠θ，V=Vm∠θ。
b.使用欧姆定律和基尔霍夫定律来建立相量表达式。
c.对电路中的频域参数应用相量法，计算电路中的电流和电压。
d.计算电源电压和电流的相位差，以确定电路中的功率因数。
无论是复数法还是相量法，分析正弦稳态电路的关键是计算电路中的电流和电压的幅值和相位。
在计算过程中，需要使用复数代数、欧姆定律、基尔霍夫定律以及频域的电路参数等相关知识。
在实际应用中，正弦稳态电路的分析主要包括以下几个方面：1.交流电路中的电阻：电阻对交流电流的影响与直流电路相同，即按欧姆定律计算。
复数法计算时，电流和电压与频率无关，可以直接使用欧姆定律计算。
2.交流电路中的电感：电感器对交流电流的响应取决于电流的频率。
复数法计算电感电压和电流时，需要将频率变量引入到电感的阻抗中。
3.交流电路中的电容：电容器对交流电压的响应取决于电压的频率。
复数法计算电容电压和电流时，需要将频率变量引入到电容的阻抗中。
4.交流电路中的复数阻抗：电路中的电感、电容和电阻组成复数阻抗。
复数阻抗可以用来计算电路中的电流和电压。
根据欧姆定律和基尔霍夫定律，可以建立复数电流和电压之间的关系。
5.交流电路中的功率因数：功率因数是电路中有功功率与视在功率之比。
在分析正弦稳态电路时，可以计算电路中电源电压和电流的相位差，从而确定功率因数。
总结起来，正弦稳态电路的分析步骤包括选择复数法或相量法、建立复数或相量表达式、计算电流和电压的幅值和相位、计算功率因数等。
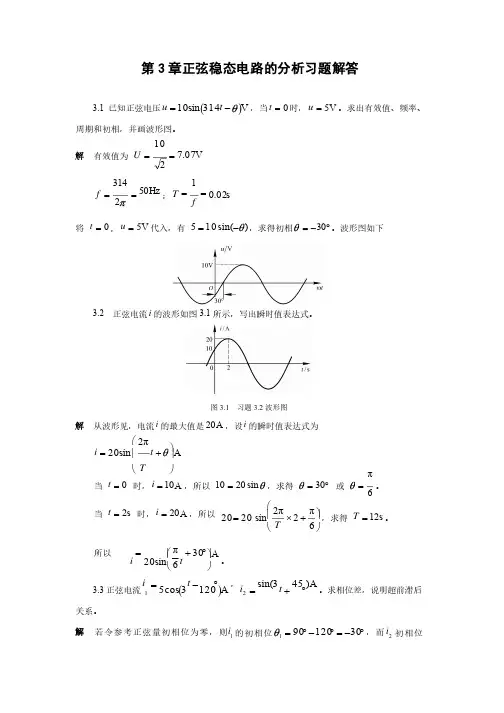
第3章正弦稳态电路的分析习题解答3.1 已知正弦电压()V314sin 10q -=t u ，当0=t 时，V 5=u 。
求出有效值、频率、周期和初相，并画波形图。
周期和初相，并画波形图。
解 有效值为有效值为有效值为 V 07.7210==UHz 502314==pf ；s 02.01==fT将 0=t , V 5=u 代入，有代入，有 )sin(105q -=，求得初相°-=30q 。
波形图如下。
波形图如下3.2 正弦电流i 的波形如图3.1所示，写出瞬时值表达式。
所示，写出瞬时值表达式。
图3.1 习题3.2波形图波形图解 从波形见，电流i 的最大值是A 20，设i 的瞬时值表达式为的瞬时值表达式为A π2sin 20÷øöçèæ+=q t T i当 0=t 时，A =10i ，所以，所以 q sin 2010=，求得，求得 °=30q 或 6π=q 。
当 s 2=t 时，A =20i ，所以，所以 ÷øöçèæ+´=6π2π2sin 2020T ，求得，求得 s 12=T 。
所以所以 A÷øöçèæ°+=306πsin 20t i。
3.3正弦电流()A 120 3cos 51°-=t i ，A )45 3sin(2°+=t i 。
求相位差，说明超前滞后关系。
关系。
解 若令参考正弦量初相位为零，则1i 的初相位°-=°-°=30120901q ，而2i 初相位°=452q ，其相位差其相位差 °-=°-°-=-=75453021q q j ， 所以1i 滞后于2i °75 角，或2i 超前1i °75 角。
