当前位置：文档之家 › 电路分析正弦稳态分析

电路分析正弦稳态分析

  • 格式：pptx
  • 大小：714.40 KB
  • 文档页数：24

下载文档原格式

  / 24

合集下载

第2章 正弦稳态电路的分析

第2章 正弦稳态电路的分析

u
l
L是一个与i、ψ无关的常数。若线圈中含有铁磁物质，则 L与i、ψ有关，不是常数。 线圈的电感与线圈的形状，几何尺寸，匝数以及周 围物质的导磁性质有关，即 SN 2 L l l为密绕长线圈的长度（m），截面为S（m2)， 匝数为N，μ为介质的磁导率。
2．自感电动势
i(t)变化
ψ变化
产生eL(t)
波形图中 正半周 u ＞ 0 , i ＞ 0 (正值),说明实际方向与参考方向相同 负半周 u ＜ 0 , i ＜0 (负值),说明实际方向与参考方向相反
+
u
_
i,u T Um O
波形： Im

wt
可见:没有设定参考方向,正负值就没有意义,波形图也表达不出 它们的变化规律
2.1.2 正弦交流电量的三要素：
u U m cos( t + ) w U m e j (wt + )的实部 正弦电压u正好等于复数
u Re [U m e j (wt + ) ] Re [U m e jwt e j ] e jwt ] (令U U e j ) Re [U m m m
现在就把பைடு நூலகம்U m U m e j U m 称为正弦电压u的最大值相量
除法：模相除，角相减。
正弦交流电量的表示法 1、瞬时表达式(即时间的正弦或余弦函数式) 2、波形图(即时间的正弦或余弦函数曲线) 3、相量法(用复数表示正弦电量的方法) (1)复数与正弦量的关系
U m e j (wt + ) U m [cos(wt + ) + j sin(wt + )]
特殊相位关系：
u, i
u i O u, i u O u, i u iw t

电路分析基础-正弦稳态分析

电路分析基础-正弦稳态分析

7. 1 正弦量的基本概念
一. 正弦量的三要素
正弦量的表达式： f(t)=Fmcos(w t+)
波形：
f(t)
Fm
T
/ O
t
Fm, , 这3个量一确定，正弦量就完全确定了。
所以，称这3个量为正弦量的三要素：
正弦量的三要素： (1) 振幅 (amplitude) ：反映正弦量变化幅度的大小。
(2) 角频率(angular frequency)w ： 反映正弦量变化快慢。
工程上说的正弦电压、电流一般指有效值，如设备铭牌 额定值、电网的电压等级等。但绝缘水平、耐压值指的是最 大值。因此，在考虑电器设备的耐压水平时应按最大值考虑。
测量中，电磁式交流电压、电流表读数均为有效值。 * 区分电压、电流的瞬时值、最大值、有效值的符号。
例：求如图周期信号的有效值。
u1(t)(V) 10
iC(t)
+
u(t)
C
-
+ 相量模型
时域形式：
相量形式：
有效值关系： IC=w CU 相位关系：i=u+90° (i 超前 u 90°)
i u
相量图
令 Xc=1/w C ，称为容抗，单位为 W(欧姆) B c = w C ， 称为容纳，单位为 S
容抗和频率成反比, 0， |XC| 直流开路(隔直)
；
关系：
|Z|—复阻抗的模；z—阻抗角。
R=|Z|cosz 或 X=|Z|sinz
|Z|=U/I ——反映u, i 有效值关系
z =u-i ——反映u, i 相位关
系
|Z| X
z
R 阻抗三角形
阻抗Z与电路性质的关系：
Z=R+j(wL-1/wC)=|Z|∠ z wL > 1/w C ，X>0， z >0，电路为感性，电压领先电流； wL<1/w C ，X<0， z <0，电路为容性，电压落后电流； wL=1/w C ，X=0， z =0，电路为电阻性，电压与电流同相。

电路原理-正弦稳态电路的分析

电路原理-正弦稳态电路的分析

对记录的数据进行分析，验证正 弦稳态电路的原理和性质。
实验结果与讨论
实验结果
通过实验观察和数据记录，可以 得出正弦稳态电路中电压和电流 的波形关系，以及元件参数对波
形的影响。
结果分析
对实验结果进行分析，验证正弦稳 态电路的基本原理，如欧姆定律、 基尔霍夫定律等。
实验讨论
讨论实验中可能存在的误差来源， 如电源稳定性、示波器的测量误差 等。同时，可以探讨如何减小误差、 提高实验精度的方法。
04 正弦稳态电路的分析实例
单相交流电路分析
总结词
分析单相交流电路时，需要计算电流、电压的有效值以及功率等参数，并考虑阻 抗、导纳和相位角等因素。
详细描述
在单相交流电路中，电压和电流都是时间的正弦函数。为了分析电路，我们需要 计算电流和电压的有效值，以及功率等参数。此外，还需要考虑阻抗、导纳和相 位角等因素，以便更准确地描述电路的性能。
实验步骤与操作
3. 观察波形
2. 连接电源
将电源连接到电路中，为电路提 供稳定的交流电压。
使用示波器观察电路中各点的电 压和电流波形，并记录数据。
4. 调整元件参数
通过调整电阻器、电容器和电感 器的参数，观察波形变化，并记 录数据。
1. 搭建正弦稳态电路
5. 分析数据
根据实验要求，使用电阻器、电 容器和电感器搭建正弦稳态电路。
相量法
1
相量法是一种分析正弦稳态电路的方法，通过引 入复数相量来表示正弦量，将时域问题转化为复 数域问题，简化计算过程。
2
相量法的核心思想是将正弦电压和电流表示为复 数形式的相量，并利用相量图进行电路分析。
3
相量法的优点在于能够直观地表示正弦量的相位 关系和幅度关系，简化计算过程，提高分析效率。

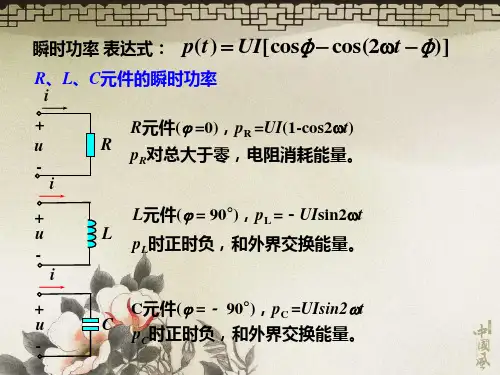
正弦稳态电路分析PPT课件

正弦稳态电路分析PPT课件
Q，并计算电源的视在功率S和功率因素cos 。
2
解法二： 采用阻抗Z计算；
·IS
+ 1
U·
2 Z 2 (1 j)(2 j) 2 3 j
1 j 2 j
3
_ j1
-j1
3 j 1 ()
Z
•
U
ZIS
(3
3j 1)50 3
(15
j 5)(V ) 3
P IS 2 Re[Z ] 52 3 75(W )
3 32 (1/ 3)2
75(W )
Q UIS sin φ
152 (5 / 3)2 5
1/ 3 32 (1/ 3)2
8.3(Var)
S UIS 152 (5 / 3)2 5 75.5(VA) cos φ 0.993
第6章 正弦稳态电路分析
例：如图电路中，已知 is 5 2 sin 2（t A ），求电源提供的P、
+
U·S_
·I1
5
j5
3 -j4
解：U s 100V I1 2 45（ A） I2 253.1（ A）
P1 I12R1 （ 2）2 5 10（W）
或： P1 USI1 cos φ1=10 2 cos 45 10(W)
P2
I
2 2
R2
22
3
12（W）
或： P2 USI2 cos φ2=10 2 cos 53.1 12（W）
例：电路如图，已知 us (t) 10 2 sin 5（t V） ，求电阻R1，R2
消耗的功率，并分析功率关系。
·I2
+ uS(t)_
R1 5 R2 3 L 1H C 0.05F
+

第四章正弦稳态电路分析

第四章正弦稳态电路分析

30
0
+1
Chapter 4
4-3 电路定律的相量形式
一、基尔霍夫定律的相量形式
i4
KCL: 时域内有: i 0
i1 i2
i3
例如: i4 i1 i2 i3 设各电路为同频率正弦量。则
Re 2I4e jt Re 2I1e jt Re 2I2e jt Re 2I3e jt Re 2 I1 I2 I3 e jt
u
Chapter 4
三. 相位差 在同一频率正弦激励下,线性电路的响应均为同频率正
弦量。
讨论同频率正弦量的相位差
设: u Um cost u i Im cost i
由相位差的定义：正弦量的相位之差。可得
t u t i u i
即:同频率正弦量相位差等于它们的初相之差。
Chapter 4
二. 相量图
已知正弦量可写出其相量,并能画出相量图。
例如: i 10 cos 314t 300 ， u 5cos 314t 600 V
I 10
26
U
5 600 V 2
或
Im
10
6
U m
560 0V
作相量图：相量的模为相量的长度,
+j U
幅角为初相。
60 I
注:在相量图上可做同频率正弦量 的加减（乘除）运算。
1 2 Im
即 Im 2I
或 I Im 2
同理可得 U m 2U
U Um 2
注:工程上所说交流电压,电流值大多为有效值,电气铭牌
额定值指有效值。交流电表读数也是有效值。
Chapter 4 4-2 正弦量的相量表示
一、复习复数知识 1. 复数的表示的形式: ①代数形式 A=a+jb

简明电路分析基础_12正弦稳态功率和能量解析

简明电路分析基础_12正弦稳态功率和能量解析

简明电路分析基础_12正弦稳态功率和能量解析正弦稳态功率和能量解析是电路分析中的重要内容，能够为我们深入理解电路中电能的转化和传输提供帮助。

本文将介绍正弦稳态功率和能量解析的基础知识和分析方法。

一、正弦稳态功率正弦稳态功率是指在正弦信号作用下，电路所吸收或输出的功率。

在分析电路功率时，通常使用的是有效（均方）值，即RMS值。

正弦信号的均方值与其幅值的平方有关，对于电压为 V(t) 的正弦信号，其均方值为Vrms=Vm/√2，其中 Vm 为幅值。

在电路分析中，常用到的功率有以下三种：1.有功功率（P）：表示电路吸收或输出的真实功率，单位为瓦特（W）。

2.无功功率（Q）：表示电路吸收或输出的无用功率，单位为乏特（VAR）。

3.视在功率（S）：表示电路吸收或输出的总功率，单位为伏安（VA）。

有功功率的公式为P = Vrms * Irms * cos(θ)，其中 Vrms 和Irms 分别为电压和电流的均方值，θ 为电压和电流的相位差。

无功功率的公式为Q = Vrms * Irms * sin(θ)，视在功率的公式为 S = Vrms * Irms。

可以看出，有功功率和视在功率与电压和电流的相位差有关，而无功功率则与相位差的正弦值有关。

相位差为正时，电流滞后于电压，此时电路吸收无功功率。

相位差为负时，电流超前于电压，此时电路输出无功功率。

二、正弦稳态能量正弦稳态能量是指电路在正弦信号作用下的能量转化和传输。

在电路中，能量主要以电压和电流的形式存在。

电压和电流可以通过以下关系计算能量：能量=电压或电流的平方×时间对于正弦信号V(t)来说，其能量可以表示为：E=(1/2)*Vm^2*T*f其中，Vm为信号幅值，T为信号周期，f为信号频率。

这个公式表示了正弦信号的能量与其幅值的平方、周期和频率之间的关系。

可以看出，能量与幅值的平方成正比，与周期和频率成正比。

正弦稳态能量在电路中有着重要的应用。

例如，在交流电路中，能量的传输通常是通过电路元件产生的电压和电流之间的相位差来实现的。

正弦稳态电路的分析

正弦稳态电路的分析

正弦稳态电路的分析1.复数法分析：a. 复数电压和电流表示：将正弦波电流和电压表示为复数形式，即I = Im * exp(jωt)，V = Vm * exp(jωt)，其中Im和Vm为幅值，ω为角频率，j为虚数单位。

b.使用欧姆定律和基尔霍夫定律来建立复数表达式。

c.找到电路中的频域参数，如电阻、电感和电容等，并使用复数法计算电路中的电流和电压。

d.计算电源电压和电流的相位差，这会决定电路中的功率因数。

2.相量法分析：a.相量表示：将电路中的电流和电压表示为相量形式，即以幅值和相位角表示，例如I=Im∠θ，V=Vm∠θ。

b.使用欧姆定律和基尔霍夫定律来建立相量表达式。

c.对电路中的频域参数应用相量法，计算电路中的电流和电压。

d.计算电源电压和电流的相位差，以确定电路中的功率因数。

无论是复数法还是相量法，分析正弦稳态电路的关键是计算电路中的电流和电压的幅值和相位。

在计算过程中，需要使用复数代数、欧姆定律、基尔霍夫定律以及频域的电路参数等相关知识。

在实际应用中，正弦稳态电路的分析主要包括以下几个方面：1.交流电路中的电阻：电阻对交流电流的影响与直流电路相同，即按欧姆定律计算。

复数法计算时，电流和电压与频率无关，可以直接使用欧姆定律计算。

2.交流电路中的电感：电感器对交流电流的响应取决于电流的频率。

复数法计算电感电压和电流时，需要将频率变量引入到电感的阻抗中。

3.交流电路中的电容：电容器对交流电压的响应取决于电压的频率。

复数法计算电容电压和电流时，需要将频率变量引入到电容的阻抗中。

4.交流电路中的复数阻抗：电路中的电感、电容和电阻组成复数阻抗。

复数阻抗可以用来计算电路中的电流和电压。

根据欧姆定律和基尔霍夫定律，可以建立复数电流和电压之间的关系。

5.交流电路中的功率因数：功率因数是电路中有功功率与视在功率之比。

在分析正弦稳态电路时，可以计算电路中电源电压和电流的相位差，从而确定功率因数。

总结起来，正弦稳态电路的分析步骤包括选择复数法或相量法、建立复数或相量表达式、计算电流和电压的幅值和相位、计算功率因数等。

第九章-正弦稳态电路的分析

第九章-正弦稳态电路的分析
（举例略）
例：9-4-2如图，列出节点电压相量方程
33
-j5Ω
1
2
5Ω 10o A
j12Ω
j5Ω -j10Ω
10Ω -j0.5A
设节点与参考节 点如图
(1 5
1 j10
1 j12
1 )U j5 1
(
1 - j5
1 )U j12 2
00
A
I 2
3
.
1
4
-
300
A
I 3.14300 A
R jωL IU2S（略）
练习9-7
习题：9-1 （b）、（e）
23
9-3 （4）
9-7 9-11
说明：9-7 求R、L时，习题解答单纯根据相量电 路列方程求解较麻烦，借助相量图分析得 到电流电压相量，然后，由
Z
R
jωL
U I
部分答案参考：
9 （1 b)Zin 2 j, Yin 0.4 j0.2
=2A。求电流表 A 读数
1
I
解：利用KCL建立电路方程
+
U
-
A
R1
-j 1
A1 I1
I2 A2
R2
1、设I2 20O
I 1
R1
U
j1 ωC
U00
1 ωC
j1 ωC
I1 1A
I1 14 5O
I14 5O
ωC
2 、I I1 I2 0 . 7 0 7 j 0 . 7 0 7 2 I 2 . 7 0 72 0 . 7 0 72 2.8( A )
Yeq Y1 Y2 Yn — 端口等效导纳
两个阻抗并联，则等效导纳：
Y
Y 1

电路原理-正弦稳态电路的分析

电路原理-正弦稳态电路的分析

& I Y = & =| Y| ∠ Y = G+jB φ U
导纳三角形
|Y|
ϕy
G
B
转换关系： 转换关系： | Y |= G2 + B2 B φy = arctg G
或
G=|Y|cosϕ y B=|Y|sinϕ y
I Y= U ϕy =φi −φu
当无源网络内为单个元件时有： 当无源网络内为单个元件时有：
2.平均功率 (average power)P 平均功率
又称有功功率
1 T 1 T Icosϕ+ U Icos(2ωt −ϕ)]dt P = ∫ pdt = ∫ [U T 0 T 0
= UIcosφ
P 的单位：W（瓦） 的单位：W（
P = UI cosφ
∑u = 0
u= R i u 或 i =G
K L: C
∑I = 0
•
K L: V
∑U= 0
或 & & I = YU
•
元件约束关系
& & 元件约束关系 U = Z I
可见，二者依据的电路定律是相似的。只要作出正弦 可见，二者依据的电路定律是相似的。只要作出正弦 电流电路的相量模型 的相量模型， 电流电路的相量模型，便可将电阻电路的分析方法推广应 用于正弦稳态的相量分析中。 用于正弦稳态的相量分析中。
i
φu φi
Im
& I
& U
& U1 = 6∠30o V & U = 4∠60oV
2
& U2
& U1
& & & U = U1 +U2 = 6∠30o + 4∠60o

电路原理与电机控制第6章正弦稳态电路分析

电路原理与电机控制第6章正弦稳态电路分析

THANKS FOR WATCHING
感谢您的观看
正弦稳态电路的功率分析是电路分析中的重要内容之一，主要涉及到有功功率、无功功率和视在功率 等概念。
有功功率是指电路中消耗的电能，用于驱动负载或产生热量。无功功率是指电路中交换的能量，用于 维持电源与负载之间的电压和电流相位关系。视在功率是指电路中电压和电流的有效值之积，用于表 示电源的总功率容量。
03
正弦稳态电路实验的目的和要求
目的
通过实验，使学生掌握正弦稳态电路 的基本原理和分析方法，培养学生对 电路理论的实际应用能力。
要求
学生需要掌握正弦稳态电路的基本概 念、元件特性、电路分析方法等理论 知识，能够独立完成实验操作，并分 析实验数据。
正弦稳态电路实验的步骤和方法
01
步骤
02
1. 准备实验器材，包括电源、电阻、电容、电感等 元件和测量仪表。
工程设计依据
正弦稳态电路的分析结果可以为工程设计提供依 据，帮助工程师更好地设计、分析和优化电路。
正弦稳态电路的应用场景
电力系统
正弦稳态电路广泛应用于电力系统的分析、设计和优化，如变压 器的设计、输电线路的参数计算等。
电子设备
在电子设备中，正弦稳态电路常用于信号处理、放大和传输等环节， 如音频设备和通信系统。
变压器和电动机在正弦 稳态电路中的特性分析
变压器在正弦稳态电路中的特性分析
变压器在正弦稳态电路中主 要起到电压变换和隔离的作 用，通过改变一次侧和二次 侧线圈的匝数比，实现电压
的升高或降低。
在正弦稳态电路中，变压器 的一次侧和二次侧电流、电 压的有效值与匝数成正比，
而相位则与匝数成反比。
变压器在正弦稳态电路中的 磁通量与电源频率、线圈匝 数和磁导率有关，而铁芯的 磁导率是常数。

电路理论第九章 正弦稳态电路的分析

电路理论第九章 正弦稳态电路的分析

(Y,G, B均为电导的量纲）
对于纯电阻电路有：YR
G
1 R
,
对于纯电感电路：YL
1
jL
j 1
L
jBL ;
Bl
1
L
称为感性电纳，简称感纳；
对于纯电容电路：YC jC jBC
对于
BC
R, L,
C ，称为容性电纳，简称容纳；
C 并联电路有：
I
I IR
IL
IC
U R
U
jL
jCU
+ U
即三者构成一个等边三角形。（如图）由相量图可
得：
U1
6
UR
UL I1
3
U s
U 2
U 2 UC
1
C
I1
U2 2U
L
tg
30
U
L
UR
C
I1
U
2 31.85F,
314 200
1
C
2 L
L
1
2 2C
159.2mH
tg30
L
R
R
L
tg30
86.6,
+
,
例题：电路如图，已知，Z1 (10 j50), Us
I
Z2 (400 j1000 ), 如果要使I2和U s
-
的相位差为90（ 正交）， 应等于多少？
U1
6
UR
3
U s
UL I1
U 2
a
Z1 + U2 Z2
- I2 I2
b
解：对于a点应用KCL有：I I2 I2 (1 )I2 要使I2和U s 的相位差为90 转化为 I 和U s 的相位差为

《电路分析》——正弦稳态分析

《电路分析》——正弦稳态分析
0 电压超前电流角 0 电压与电流同相 0 电压滞后电流角 180 电压与电流反相
>0， u超前i 角，或i 落后u 角(u 比i先到达最大值)；
u, i u i
O
t
yu yi

<0， i 超前 u 角，或u 滞后 i 角,i 比 u 先到达最大值。
Im A2
0
图解法
A1 Re
(2) 乘除运算——采用极坐标形式
若 A1=|A1| 1 ，A2=|A2| 2
则:
A1 A2

A1 e j1
A2 e j2

A1
A e j(12 ) 2
A1 A2 1 2 乘法：模相乘，角相加。
A1 A2

| A1 |θ1 | A2 |θ2
几种不同值时的旋转因子
Im
(1) ,
jI jI
I
2
j
e2
cos

j sin

j
2
2

I I
0
Re

jI

jI
(2) ,
jபைடு நூலகம்
e2
cos(
)
j sin(
)
j
2
2
2
(3) , e j cos( ) j sin( ) 1
其它非正弦的周期信号不能照搬这个关系式；
（2）工程上所说的正弦电压和电流的大小都是指有效值； （3）一般电压表和电流表的刻度都是按有效值来标定的； （4）交流电气设备铭牌上所标定的电压、电流值都是有效 值。如“220V，100W”的白炽灯，是指它的额定电压的有效 值是220V。

第7章 正弦稳态电路分析

第7章 正弦稳态电路分析

第7章 正弦稳态电路分析
二、正弦量的相量表示 著名科学家 • 斯坦梅茨(Charlea Proteus Steinmetz 1865~1923) • 斯坦梅茨是德国一澳大利亚数学家和工程师。他最 伟大的贡献就是在交流电路分析中引入了向量分析法， 并以其在滞后理论方面的著作而闻名。 • 出生于德国的布勒斯劳，一岁时就失去了母亲，在 即将在大学完成他的数学博士论文时，由于政治活动， 被迫离开德国，到瑞士后又去了美国，1893年受雇于美 国通用电气公司，这一年他发表论文，首次将复数应用 于交流电路的分析中，其后出版了专著《交流现象的理 论和计算》，1901年成为美国电气工程师协会(IEEE)主 席。

T
0
i 2 ( t )dt
周期电流有效值定义为：
1 T 2 I i (t )dt T 0
第7章 正弦稳态电路分析
一、正弦量的概念 周期电流有效值定义为：
1 T 2 I i (t )dt T 0
def
当信号为正弦信号时，设： i(t)=Imsin( t+ ) 有效值为：
1 I T
第7章 正弦稳态电路分析
一、正弦量的概念 同理，可得正弦电压有效值与最大值的关系： 1 U Um 或 U m 2U 2 若一交流电压有效值为U=220V，则其最大值为Um311V； U=380V， Um537V。
工程上说的正弦电压、电流一般指有效值，如设备铭牌额 定值、电网的电压等级等。但绝缘水平、耐压值指的是最大值。 因此，在考虑电器设备的耐压水平时应按最大值考虑。 测量中，电磁式交流电压、电流表读数均为有效值。 *注意 区分电压、电流的瞬时值、最大值、有效值的符号。
i(t)=Imsin( t+ i)
u i j

电路分析原理第六章 正弦稳态电路分析

电路分析原理第六章 正弦稳态电路分析
三、频域电路 四、电阻器上的功率
一、线性定常电阻器特性方程的时域形式
图６-８ 电阻器上的正弦电流和电压 a)时域电路 b)在关联参考方向下，i ( c)相量图 d)频域电路
0)
二、线性定常电阻器特性方程的相量形式 根据复数相等理论，该式指出两点：
1) ＵＲ＝ＲＩ，或Ｉ＝ＧＵＲ(模相等)，即在电阻器上，电流、
2.复平面 复平面是一个直角坐标平面，横轴表示实数轴，纵轴表示虚数
轴，如图６-３所示。
3.复数的几种表示形式 (1)代数式 复数Ａ＝a+jb称为代数式，或直角坐标形式。
(2)指数式
(3)极式 (4)共轭复数 复数Ａ＝a＋jb的共轭复数为＝a－jb； 复数Ａ ＝｜Ａ｜复数为＝｜Ａ｜ 。
(1)代数式
电压有效值之间满足欧姆定律(对此，人们称这两个式子为有效 值形式的欧姆定律)； 2) Ｒ与同相(辐角相同)【思考 下列写法正确吗? 同相(2) uＲ与i同相】。 (1)ＵＲ与Ｉ
三、频域电路
图６-９ 在关联参考方向下， i
四、电阻器上的功率 1.瞬时功率
2.平均功率
电路分析原理（上册）
第六章
正弦稳态电路分析
第一节 周期函数的平均值与有效值
第二节 第三节 第四节 第五节 第六节 第七节 复数及其运算 正弦时间函数的相量表示 正弦稳态电路中的电阻器 正弦稳态电路中的电感器 正弦稳态电路中的电容器 基尔霍夫定律的相量形式
第八节 ＲＬＣ串联电路—阻抗
第九节 ＧＣＬ并联电路—导纳 第十节 简单导抗电路分析
第十一节 串联谐振电路
第六章
正弦稳态电路分析
第十二节 *第十三节 第十四节 ∗第十五节
并联谐振电路 串并联电路的谐振 复杂线性电路分析 电路的对偶性质

正弦稳态电路分析解读

正弦稳态电路分析解读
i 10 2 cos(314 t 30 0 ) A
求：（1）正弦量的最大值、有效值； （2）角频率、周期、频率； （3）初相角、相位差。
解 ： （1）最大值 Um=220 2 V, Im=10
有效值 U=220V， I=10A
2A
（2）角频率ω=314 rad/s, 频率f=50Hz, 周期T=0.02s
根据有效值的定义有：
I 2 RT 0Ti2 Rdt
正弦电流的有效值为：
I
1 T
0Ti 2 dt
1 T
0T
I
2 m
cos2
(t
i)dt
I m 0.707 I m 2
同理，正弦电压的有效值为：
U Um 0.707Um 2
正弦电动势的有效值为：
E
Em 2
0.707 Em
在正弦量的三要素中，一般用有效值来代替最大值表示正 弦量的大小，在工程上，通常所说的正弦电压、电流的大 小都是指其有效值。
e Em cos(t e )
u U m cos(t u )
i I m cos(t i )
4.1.1 正弦量的三要素
正弦量的特征表现在变化的快慢、大小和初始值三个方面， 它们分别由角频率、幅值和初相来确定，统称为正弦量的 三要素。
以正弦电流为例
i Im cos(t i )
幅值
角频率
初相
的初始值
规定初相角的绝对值不超过
即 ≤≤
如果遇到初相角大于 时，应加 初相角小 于 时，应加 2
规定
2 ，如果遇到
来使初相角符合
4.1.2 正弦量的有效值
有效值用来表示正弦量大小
正弦电流的有效值：
让周期电流i和直流电流I分别通过两 个阻值相等的电阻R，如果在相同的 时间T内，两个电阻消耗的能量相等， 则称该直流电流I的值为周期电流i的 有效值。

正弦稳态分析-电路分析

正弦稳态分析-电路分析

第二节 电阻、电感和电容的相量形式的VCR
一、R元件：
设 : iR 2IR cos(ωt i) 则 : uR R iR 2RI R cos(ωt i )
U
R

RI R
u i
即: UR RIR
IR R UR
UR Ψi IR
二、L元件： 设 : iL 2IL cos(ωt i) ,
知：A a jb
则: A a 2 b2 , φ arctg b , A a 2 b2tg 1 b Aφ
a
a
若知：A Aφ
则: a A cos φ, b A sin φ, A A cos φ j A sin φ
（3）复数的四则运算 相等：两复数的实部和虚部分别相等。
则 45 30 15
解：i2 20cos(314t 30 90) 20cos(314t 60)
则 45 (60) 105
或i1
10sin( 314t 45 90) 则 135 30 105

10sin(
例2：(5+j4) ×(6+j3)=18+j39
2ndF CPLX 5 a 4 b × 6 a 3 b =显示“18” b 显示
“39”
例3： 3 j4 5(126.87)
3 +/- a 4 +/- b 2ndF →rθ 显示“5” b 显示“-126.8698…”
例4： 10 ∠-60° =5-j8.66…
同理
t
idt
的相量为:

I
jω

ωI

90

电子科大《电路分析》第10章 正弦稳态分析

电子科大《电路分析》第10章 正弦稳态分析

解： 2f 100 rad / s
u1 (t ) 50 cos(100t 30)V u2 (t ) 100 cos(100t 150)V
今后我们所见到的正弦波无非以三种形式来描述：
u2 (t ) 100 cos(100t 150)V I1m 560 A 2. I m I m I cos I sin I1m 6 j 7 A 3. I m m m
§10-4 三种基本电路元件伏安关系的相量形式
电阻:
U m RI m ,
U RI
U RI ,
u i
同相 正交
正交
电感:
U m jLI m ,
U jLI
U LI ,
u i 90
I jCU
电容:
I m jCU m ,
12 90,13 210, 23 120
13 150
规定相位差
二、正弦电压电流的相量表示
由欧拉公式有:
e
j
cos j sin
e
j (t )
cos(t ) j sin( t )
U e j 令U m m
§10-3 基尔霍夫定律的相量形式
虽然相量法将微分方程在正弦激励下的特解化成了
复数方程的求解，但对高阶电路，微分方程的建立仍是
一件很困难的工作。
对正弦激励下的电路，能否象直流激励下的电阻电 路那样，用观察法直接写出复数方程，回答是肯定的. 只要引入KCL, KVL和元件VCL的相量形式及相量模 型，就可以将电阻电路的所有分析方法推广到正弦稳态 电路。
一、简单推导
i1 i2 i3 0
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

相量模形
j5 j1
•
i(t) 10
•
US
+
100o V 10
I
-
即相量模型是利用相量法分析正 弦稳态电路的假想模型。
2.根据 KCL 、KVL 和元件 VCR 相 量形式建立复数方程或相应公式，求 出电压或电流相量。 3.由所求出的相量写出相应的正弦量。
例 图示电路，
i 3
0.6H iL
已知 iL(t)
2 cos10tA，
+ _
uS
0.1F uc
0.2H
求 i(t),uc(t),us(t).
•
I
3
+•
解（1）作出相量模型如图 _Us
j6
•
IL 100 A
•
Ic j1
•
Uc
j2
（2）由相量模型：
Uc UL j2IL j2V 2900 V
Ic
Uc j1
2A ,
I Ic IL 1A 11800 A
Y Y串 YL 0.12S（纯电阻网络）
U
Is Y
0.6600 0.12
5600 V
IL YLU j0.16 5600
•
Is
0.8 300 A
也可用分流公式： 0.660o A
•
IL
3
•
U
j4
j0.16S
IL
Is
YL Y串 YL
0.6600
j0.16 0.12
0.8
300 A
的相量
解：画出相量模型。
∵Z 1.5 j1(1 j2) 15 0.5 j1.5 2.536.90 K 1 j1
∴I Us 40 16 36.90 mA Z 2.536.9
由分流公式：
IL
I 1 1
j2 j1
• 1.5k 1k
I
•
•
IL
Ic
•
Us
j1k
25.3 55.30 mA
•
I2 Y2
Z2
例 已 知 is (t) 0.6 2 cos(10t 600 )A ， 求u(t) 和
iL (t)。
iL
•
IL
3
•
Is
3
iS
u
0.625H
0.025F
0.660o A
•
U
j4
j0.16S
解：（1）画出相量模型
∵ Y串
3
1 j4
5
1 53.10
0.2 53.10 0.12 j0.16S
1H
4
0.25F C
Z(j3) 4 j(3 1 ) 4 j1.7 0.25 3
2.串联电路的分压公式
•
•
第K个阻抗上的
U1 U2
Z1
Z2
电压相量为
•
U
Uk
U
Zk
n
Zk
k 1
若只有两个阻抗串联
U1
U
Z1 Z1 Z2
U2
U
Z2 Z1 Z2
_ Zn
•
Un
例 已知us (t) 10 2 cos 20tV，求i(t) 和uc (t)
•
30o v
I1
j1
•
I2
•
I3 •
1 I 2
j4v
1、 网孔分析：设网孔电流如图
(1 j1)I1 I1 (1
I2 j1)I2
3 j4
I1
3.218.430
（2）由相量与正弦波的对应关系得
u(t) 5 2 cos(10t 600 )V
iL (t) 0.8 2 cos(10t 300 )A
i 1.5k 1k
us
iL
ic
1 H 1 F
3
6
• 1.5k 1k
I
•
•
IL
Ic
•
Us
j1k
400o v
j2k
例 已知us (t) 40 2 cos(3000t)V，求 i(t) 、iL (t) 、ic (t)
20 450 V 2
或
Uc
分压
Us
Zc Z
10 10
j20 2 450
20 450V 2
上面已得
U c
20 2
450
V
•
I
1
450 A ）
2
（2）由正弦量与相量的对应关系得
i(t) cos(20t 450 )A
uc (t) 20cos(20t 450 )V
以上两式验证i c 超前uc 900 。
400o v
j2k
Ic
I
1
j1 j1
11.398.10
mA
作业：（443页）10-26，10-27，10-35，10-37
§10-6 一般正弦稳态电路分析 建立了阻抗、导纳以及相
量模型之后， 电阻电路的公式和 分析方法完全可以推广到正弦稳 态电路，现以例说明。
例 10-13 图示电路，us1(t) 3 2 cos 2tV ，
3.导纳并联电路
等效导纳Y Y1 Y2 Y3
并联支路上的电流I1
I
Y1 Y
若只有两条支路并联：
Y Y1 Y2
Z Z1 Z2 Z1 Z2
I1
I Y1 Y1 Y2
I Z2 Z1 Z2
I2
I Y2 Y1 Y2
I Z1 Z1 Z2
I
•
I
•
•
I1
Y1
•
I2
Y2
•
I3
Y3
•
I1 Y1
Z1
us2 (t) 4 2 sin 2tV求i1(t) 。
i1 0.5H
us1
0.5F i2
i3
1
us2
• j1 I1
•
30o v
I1
j1
•
I2
•
I3 •
1 I 2
j4v
解：画出相量模型后，教材中分别用支路 分析法，网孔分析法，节点法，叠加定理 和戴维宁定理进行了分析，现仅将思路讨 论如下：
• j1 I1
§10-5 正弦稳态的相量分析
一、 相量法分析正弦稳态的主要步骤 1、 画出电路的相量模型 它和原电路具有相同的拓扑结构，其中电 压、电流用相量表示，元件用阻抗或导纳表 示，各相量电压、电流与原电路的参考方向 相同。
例如 已知us (t) 10 2 cos10tV
0.5H
+
uS (t)
-
0.1F
Us (3 j6)I Uc 3 j6 j2 3 j4 5 126.90 V
Uc 2900 V I 11800 A Us 5 126.90 V
(3）uc(t) 2 2cos(10t 900 )V
i(t) 2 cos(10t 1800 )A us (t) 5 2 cos(10t 126.90 )V
二、 阻抗串联和并联电路分析
1、 串联电路的等效阻抗
n
Z Z1 Z2 ...... Zn Zk
k 1
例 求图示电路当分别为 1、2、3rad/s 时的等效阻抗。
解：Z R jL 1 R j(L 1 )
jc
c
代入元件值和得
R
L
Z(j1) 4 j(1 4) 4 j3 Z(j2) 4 j(2 2) 4
0.5H 2.5mF i
• j10 j20 I
us +
uc 10
•
+
•
US 100o v UC 10
-
-
解（1）画出相量模型
∵Z j10 j20 10 10 j10 10 2 450
∴I Us Z 10
10 2
450
1 450 A 2
U c
VCR
j20I
j 20 450 2