下载文档原格式
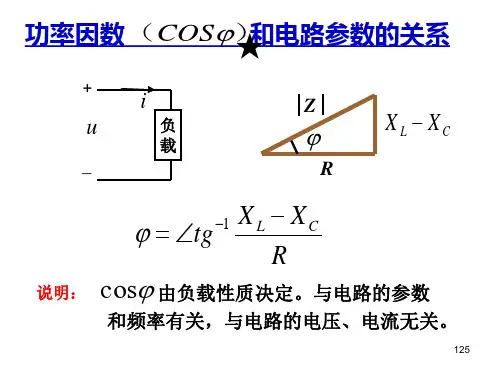
正弦稳态电路的功率公式——深入浅出理解正弦稳态电路是电路理论中的基本概念，其功率公式是电学中的热门话题。
本文将深入浅出地介绍正弦稳态电路的功率公式，帮助读者系统地理解和掌握这一重要理论。
首先要明确的是，正弦稳态电路的功率公式是指在周期性交流电源作用下，电路中所传递的功率。
正弦稳态电路中，电流和电压均为正弦波形，其功率公式可以表示为：P=VIcosφ其中，P表示电路的有功功率，V和I分别表示电路中的电压和电流，φ表示电路中电流和电压之间的相位角。
我们可以通过下面的图例来进一步理解这个公式：在图例中，V是电路中的电压，I是电路中的电流，它们的波形均为正弦函数。
在时间t=0时，电流I的相位角为0，电压V的相位角为θ，因此φ的值等于θ。
通过对P=VIcosφ公式的应用，我们可以计算出电路中的有功功率P。
下面举个例子来说明如何求解正弦稳态电路中的功率。
假设我们有一个电路，电压源为220V，电阻为10Ω，交流频率为50Hz，我们需要求解该电路的功率。
首先，我们需要计算电路中的电流，通过欧姆定律可知电流I=V/R，因此I=22A。
接下来，我们需要求解相位角φ。
由于电路中只有电阻，电流和电压之间没有相位差，因此φ=0。
因此，根据功率公式，我们可以计算得到电路中的有功功率P=VIcosφ=22*220*1=4840W。
总之，正弦稳态电路的功率公式是电学中的基本概念，是电路分析和设计中必须掌握的知识点。
本文通过生动的示意图和实例应用，帮助读者深入浅出地理解和掌握正弦稳态电路的功率公式。
无论你是电学专业的学生，还是从事电路设计和调试等工作的工程师，掌握这一知识点都是非常重要的。
正弦稳态电路的功率公式在电路中，功率是电能转换的重要指标之一。
而对于正弦稳态电路，我们可以通过一条简单而有效的公式来计算其功率。
本文将详细介绍正弦稳态电路的功率公式，并解释其背后的原理和应用。
一、正弦稳态电路的功率公式正弦稳态电路是指电路中的电流和电压都是正弦波形式，并且其频率保持不变。
在这种情况下，我们可以使用以下功率公式来计算电路中的功率：P = Vrms * Irms * cos(θ)其中，P表示电路的功率，Vrms表示电压的有效值，Irms表示电流的有效值，θ表示电压和电流之间的相位差。
二、功率公式的原理解释为了更好地理解功率公式的原理，我们可以从电能转换的角度来解释。
在正弦稳态电路中，电流和电压都是周期性变化的，而功率则是电能转化的速率。
根据能量守恒定律，电路中产生的功率等于电能的消耗速率。
在公式中，Vrms和Irms分别表示电压和电流的有效值。
有效值是指在一个周期内，电压和电流的平方值的平均值的平方根。
有效值可以反映电压和电流的实际大小，而不受正弦波形式的影响。
而c os(θ)则表示电压和电流之间的相位差。
相位差是指电压和电流的波形之间的时间差，它可以是正值、负值或零值。
当相位差为零时，电压和电流完全同相，功率取得最大值。
当相位差为正值或负值时，电压和电流存在一定的错位，功率将减小。
因此，正弦稳态电路的功率公式可以通过电压和电流的有效值以及它们之间的相位差来计算电路的功率。
三、功率公式的应用功率公式在电路分析和设计中有着广泛的应用。
它可以帮助我们计算电路中的功率消耗，并进一步优化电路的设计。
功率公式可以用于计算电路中不同元件的功率消耗。
例如，我们可以通过测量电压和电流的有效值，并计算它们之间的相位差，来确定电阻、电容或电感元件的功率消耗。
功率公式可以用于分析电路中的功率传递和传输效率。
通过计算电路中不同节点的功率，我们可以了解能量在电路中的分布情况，找出能量损失的原因，并进一步改进电路的效率。
