正弦稳态电路的分析
- 格式：doc
- 大小：389.00 KB
- 文档页数：15
下载文档原格式
合集下载
正弦稳态电路分析和功率计算
2
Y = 0.1 + j0.2S
0.025F 0.1S
0.02F
十、利用相量图求解电路
例 如图所示电路，uS 2US cost ，求输出电压 uO(t) 对 uS(t) 的相位关系。
C
解：（一）解析法
+
+
1
uS
R uO
–
–
（二）相量图法
U O②
I jC
+ US
U C
R
+ UO
–
–
I ①
③ U C
直流电阻电路：（ m个网孔，m个网孔电流 Im1 , Im2 , … Imm）
R11Im1 R12Im2 R1mImm uS11
R
21I
m1
R
22I
m2
R 2mImm
uS22
R m1Im1 R m2Im2 R mm Imm uSmm
正弦稳态电路：（ m个网孔，m个网孔电流 Im1 , Im2 , … Imm）
ZZ1211IImm11
Z12I m 2 Z 22I m 2
Z1m I mm Z 2 m I mm
U S11 U S22
Zm1Im1 Zm2Im2 Zmm Imm U Smm
例 uS = 6cos3000t V，求正弦稳态时的 i1 , i2 。
i1 1k
+2000–i1 i2
uS
(3)
Z
U I
U I
u i
= R + jX = |Z| Z
Z R2 X2
Z
arctg
X R
ZU I
Z = u – i
(4) 阻抗的性质
正弦稳态电路的分析
Z1=Z2=-j200Ω
14、如图所示14正弦稳态电路，R=XL=5Ω，I1=10A，
UC=100V，XC=10Ω，
试求U和I。
解：设 2=I2 A
=50 V
=100 2=10 A 1=10 A
所以，I= =10 AI12+I2=I22
易知 与 同相
U= UC=100 V
15、如图15a所示正弦稳态电路，R1=1KΩ，R2=2KΩ，L=1H，求Ucd=Uab时C的值。
解：电路的总阻抗为
Z=-jXC+ = +j( -XC)
当XC=1Ω和XC=2Ω，可以列出如下两个方程
(1)
(2)
解（1）、（2）得，R=2 Ω，XL=2Ω
4、图4所示工频正弦电流电路中，U=100V，感性负载Z1的电流I1=10A，功率因数λ1=0.5，R=20Ω。
（1）求电源发出的有功功率、电流I、功率因数λ
(3)u= u1+u2+u3的表达式
解：（1）将 ， 写成标准指数形式，即
=-100∠150°V=100∠-30°V
=-100+j100 V=100 ∠135°V
根据相量和正弦量的关系，可得
u1=50 cos(314t+60°) V，u2=100 cos(314t-30°) V
u3=200cos(314t+135°) V
解： =Y =( ) = 45°
I= A
11、列出图11所示电路相量形式的回路方程和结点方程。
解：设各回路方向如图所示。
回路方程如下：
（1）
（2）
（3）
（4）
- = S（5）
选结点0作为参考结点，结点方程如下:
14、如图所示14正弦稳态电路，R=XL=5Ω，I1=10A，
UC=100V，XC=10Ω，
试求U和I。
解：设 2=I2 A
=50 V
=100 2=10 A 1=10 A
所以，I= =10 AI12+I2=I22
易知 与 同相
U= UC=100 V
15、如图15a所示正弦稳态电路，R1=1KΩ，R2=2KΩ，L=1H，求Ucd=Uab时C的值。
解：电路的总阻抗为
Z=-jXC+ = +j( -XC)
当XC=1Ω和XC=2Ω，可以列出如下两个方程
(1)
(2)
解（1）、（2）得，R=2 Ω，XL=2Ω
4、图4所示工频正弦电流电路中，U=100V，感性负载Z1的电流I1=10A，功率因数λ1=0.5，R=20Ω。
（1）求电源发出的有功功率、电流I、功率因数λ
(3)u= u1+u2+u3的表达式
解：（1）将 ， 写成标准指数形式，即
=-100∠150°V=100∠-30°V
=-100+j100 V=100 ∠135°V
根据相量和正弦量的关系，可得
u1=50 cos(314t+60°) V，u2=100 cos(314t-30°) V
u3=200cos(314t+135°) V
解： =Y =( ) = 45°
I= A
11、列出图11所示电路相量形式的回路方程和结点方程。
解：设各回路方向如图所示。
回路方程如下：
（1）
（2）
（3）
（4）
- = S（5）
选结点0作为参考结点，结点方程如下:
第九章正弦稳态电路分析
矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。
邱关源《电路》第九章正弦稳态电路的分析1
第九章 正弦稳态电路的分析
BUCT
9. 1 阻抗和导纳 9. 2 阻抗（导纳）的串联和并联 9. 3 电路的相量图 9. 4 正弦稳态电路的分析 9. 5 正弦稳态电路的功率 9. 6 电路的谐振
1
9. 3 电路的相量图
一、RL、RC串联电路
IR
+
U _
+
_ UR +
jL
U_L
P188
U
j
0
8—11 BUCT
1, 纯电阻 0， 纯电抗
X<0, j < 0 , 容性负载， 超前功率因数
例：cos j = 0.5 (滞后)，则j =60o(电压领先电流60o)。
一般用户： 异步电机 空载 cosj =0.2~0.3 满载 cos j =0.7~0.85
日光灯
cosj =0.45~0.6
17
功率因数的提高
k
1
Qk
0
14
* 复功率守恒, 不等于视在功率守恒.
BUCT
I
+
U_
+ U 1 _
+
U_ 2
S UI* (U1 U 2 )I * U1I * U 2I* S1 S2
b
一般情况下： S Sk k 1
例：
S S2 Q2 S1 P2
Q1 P1
R2 UR2 I 33.9 1.73 19.6W
L UL2 I 72.45 1.73 41.88W
L2 41.88 314 0.133H
12
复功率
BUCT
为了用相量U和I来计算功率，引入“复功率”
I
+
BUCT
9. 1 阻抗和导纳 9. 2 阻抗（导纳）的串联和并联 9. 3 电路的相量图 9. 4 正弦稳态电路的分析 9. 5 正弦稳态电路的功率 9. 6 电路的谐振
1
9. 3 电路的相量图
一、RL、RC串联电路
IR
+
U _
+
_ UR +
jL
U_L
P188
U
j
0
8—11 BUCT
1, 纯电阻 0， 纯电抗
X<0, j < 0 , 容性负载， 超前功率因数
例：cos j = 0.5 (滞后)，则j =60o(电压领先电流60o)。
一般用户： 异步电机 空载 cosj =0.2~0.3 满载 cos j =0.7~0.85
日光灯
cosj =0.45~0.6
17
功率因数的提高
k
1
Qk
0
14
* 复功率守恒, 不等于视在功率守恒.
BUCT
I
+
U_
+ U 1 _
+
U_ 2
S UI* (U1 U 2 )I * U1I * U 2I* S1 S2
b
一般情况下： S Sk k 1
例：
S S2 Q2 S1 P2
Q1 P1
R2 UR2 I 33.9 1.73 19.6W
L UL2 I 72.45 1.73 41.88W
L2 41.88 314 0.133H
12
复功率
BUCT
为了用相量U和I来计算功率，引入“复功率”
I
+
第3章 正弦交流稳态电路(5.6.7.8节)
故电压表的读数为141.1V，电流表的读数为10A。
例二： 在图3．5-2(a)所示电路中，已知R1=48Ω ，R2=24Ω ，
R3=48Ω ,R4=2Ω ，
3
XL=2．8Ω ， U 1
=220∠0°V，U
2
=220∠-120°V，U
=220∠120°V。
试求感性负载上的电流L。
例一：
如下图所示电路中，已知I1=10A，UAB=100V。求电压表V和电 流表A的读数。
解：设
U AB 为参考相量，即 U AB =100∠0°V，则
U AB 0 I2 10 2 45 A, I1 10900 A 5 j5
I I1 I 2 10900 10 2 450 1000 A U c1 I ( j10) j100 V U U c1 U AB j100 V 100 V 100 2 450 V 141.1 450 V
§3．5正弦稳态电路的分析
3．5．1相量分析法 在正弦稳态电路的分析中，若电路中的所有元件都用阻
抗模型表示，电路中的所有电压和电流都用相量表示，所
得电路的相量模型将服从相量形式的欧姆定律和基尔霍夫 定律，此时列出的电路方程为线性的复数代数方程(称为相 量方程)，与电阻电路中的相应方程类似。这种基于电路的 相量模型对正弦稳态电路进行分析的方法称为相量分析法。
QC=-P(tanφ L-tanφ )
例：
(3．7-4)
已知某目光灯电路模型如图3．7-1(a)中的实线所示。图中L为铁心线圈，称 为镇流器，R为灯管的等效电阻。已知电源电压U=220V，f=50Hz，日
例二： 在图3．5-2(a)所示电路中，已知R1=48Ω ，R2=24Ω ，
R3=48Ω ,R4=2Ω ，
3
XL=2．8Ω ， U 1
=220∠0°V，U
2
=220∠-120°V，U
=220∠120°V。
试求感性负载上的电流L。
例一：
如下图所示电路中，已知I1=10A，UAB=100V。求电压表V和电 流表A的读数。
解：设
U AB 为参考相量，即 U AB =100∠0°V，则
U AB 0 I2 10 2 45 A, I1 10900 A 5 j5
I I1 I 2 10900 10 2 450 1000 A U c1 I ( j10) j100 V U U c1 U AB j100 V 100 V 100 2 450 V 141.1 450 V
§3．5正弦稳态电路的分析
3．5．1相量分析法 在正弦稳态电路的分析中，若电路中的所有元件都用阻
抗模型表示，电路中的所有电压和电流都用相量表示，所
得电路的相量模型将服从相量形式的欧姆定律和基尔霍夫 定律，此时列出的电路方程为线性的复数代数方程(称为相 量方程)，与电阻电路中的相应方程类似。这种基于电路的 相量模型对正弦稳态电路进行分析的方法称为相量分析法。
QC=-P(tanφ L-tanφ )
例：
(3．7-4)
已知某目光灯电路模型如图3．7-1(a)中的实线所示。图中L为铁心线圈，称 为镇流器，R为灯管的等效电阻。已知电源电压U=220V，f=50Hz，日
第9章 正弦稳态电路的分析(答案)
第9章 正弦稳态电路的分析 答案例 如图所示正弦稳态电路，已知I1=I2=10A,电阻R 上电压的初相位为零，求相量•I 和•S U 。
解： 电路中电阻R 和电容C 并联，且两端电压的初相为0。
由电阻和电容傻姑娘的电压与电流的相位关系可知：电阻电流•1I 与电压•R U 同相，电容电流•2I 超前电压•R U 相角90○，故ο0101∠=•I A ο90102∠=•I A由KCL 方程，有 ()101021j I I I +=+=•••A由KVL 方程，有 ︒•••∠==++-=+=9010010010010010010101j j I I j U S V例 如图所示正弦稳态电路，R 1=R 2=1Ω。
（1）当电源频率为f 0时，X C2=1Ω，理想电压表读数V 1=3V ，V 2=6V ，V 3=2V,求I S 。
（2）电路中电阻、电容和电感的值不变，现将电源的频率提高一倍，即为2 f 0，若想维持V 1的读数不变，I S 问应变为多少如果把电源的频率提高一倍，而维持V1的读数不变，即R1上的电压有效值U R1＝3V，那么R1上的电流的有效值I也不变，此时仍把•I设置为参考相量，故︒•∠=03I A。
由于L和C1上的电流•I不变，根据电感和电容上电压有效值与频率的关系，电源的频率提高一倍，电感上电压表的读数增大一倍，而电容上电压表的读数降为原来的一半，故电源得频率提高一倍，X C2也降为原来得一半，即所以例如图所示正弦稳态电路，已知I1＝10A，I2=20A，R2=5Ω，U=220V,并且总电压•U与总电流•I同相。
求电流I和R，X2，X C的值。
例 如图所示正弦稳态电路，已知有效值U 1=1002V, U=5002V ，I 2=30A ，电阻R=10Ω，求电抗X 1，X 2和X 3的值。
由电路可得两边取模得已知2550=U V ，所以6002=U V ，故有。
第五章 正弦稳态电路分析
5.3.2 复数的概念 复数运算是正弦稳态电路分析法的数学工具，掌握复数运算和如何将正弦信号与复 数建立关系是关键。 1. 正弦信号与复数之间的关系 欧拉公式
e jx = cos x + j sin x
根据欧拉公式有
U me j(ωt+θi ) = U m cos(ωt + θi ) + jU m sin(ωt + θi )
n•
∑ ∑ I km = 0 或
Ik =0
k =1
k =1
KVL 相量形式（对于回路）
∑n • U km = 0
或
k =1
3. 电路元件的相量表示
•
•
电阻元件：U = R I
∑n • Uk =0
k =1
•
•
电感元件：U = jωL I
•
电容元件：U =
1
•
I =−j
1
•
I
jωC
ωC
4. 相量模型 所谓相量模型，就是将电路中正弦电压源和电流源用相量形式表示，电压变量和电 流变量用相量形式表示，电阻、电感和电容用阻抗形式表示。
电阻阻抗形式： Z R = R
电感阻抗形式： Z L = jωL
电容阻抗形式： ZC
=
1 jωC
=−j 1 ωC
5.3.4 电路谐振
•
•
谐振条件，对于二端口网络，端口电压U 与端口电流 I 同相位。根据这一条件
第五章 正弦稳态电路分析 •55•
可知，只有当阻抗的虚部为零才能满足这个条件。使虚部为 0 的频率为谐振频率。 谐振分为串联谐振和并联谐振。 串联谐振常用于无线接收设备中，并联谐振常用于带通滤波、选频电路等。
第九章 正弦稳态电路的分析
1 1 Y = = −53.13°S = (0.024 − j0.032)S (感 ) 性 eq Zeq 25
9-2
电路的相量图
分析阻抗（导纳） 分析阻抗（导纳）串、并联电路时，可以利用相关的 并联电路时， 电压和电流相量在复平面上组成的电路的相量图。 电压和电流相量在复平面上组成的电路的相量图。 1. 并联电路相量图的画法 并联电路相量图的画法 ① 参考电路并联部分的电压相量。 参考电路并联部分的电压相量。 根据支路的VCR确定各并联支路的电流相量与电压相 ② 根据支路的 确定各并联支路的电流相量与电压相 量之间的夹角。 量之间的夹角。 根据结点上的KCL方程，用相量平移求和法则，画出结点 方程， ③ 根据结点上的 方程 用相量平移求和法则， 上各支路电流相量组成的多边形。 上各支路电流相量组成的多边形。
R = G2GB2 , +
−B X = G2+B2
1 | Y |= , φZ = −φY |Z|
已知：R=15Ω, L=12mH, C=5µF, u =100 2cos(5000t) 例9-1 已知 试求:(1)电路中的电流 i, （瞬时表达式）和各元件的 电路中的电流 瞬时表达式） 试求 电压相量； 电路的等效导纳和并联等效电路 电路的等效导纳和并联等效电路。 电压相量；(2)电路的等效导纳和并联等效电路。 jω L R L R • + • - + UL + + uR - + uL - + + + uS C
第二种分解方法
第一种分解方法： p(t) =UI[cosϕ + cos(2ωt −ϕ)] 第一种分解方法： p UIcosϕ 恒定分量 恒定分量 u i
O
正弦稳态电路分析PPT课件
Q，并计算电源的视在功率S和功率因素cos 。
2
解法二： 采用阻抗Z计算；
·IS
+ 1
U·
2 Z 2 (1 j)(2 j) 2 3 j
1 j 2 j
3
_ j1
-j1
3 j 1 ()
Z
•
U
ZIS
(3
3j 1)50 3
(15
j 5)(V ) 3
P IS 2 Re[Z ] 52 3 75(W )
3 32 (1/ 3)2
75(W )
Q UIS sin φ
152 (5 / 3)2 5
1/ 3 32 (1/ 3)2
8.3(Var)
S UIS 152 (5 / 3)2 5 75.5(VA) cos φ 0.993
第6章 正弦稳态电路分析
例：如图电路中，已知 is 5 2 sin 2（t A ），求电源提供的P、
+
U·S_
·I1
5
j5
3 -j4
解：U s 100V I1 2 45（ A） I2 253.1（ A）
P1 I12R1 （ 2）2 5 10（W）
或： P1 USI1 cos φ1=10 2 cos 45 10(W)
P2
I
2 2
R2
22
3
12（W）
或： P2 USI2 cos φ2=10 2 cos 53.1 12（W）
例：电路如图，已知 us (t) 10 2 sin 5（t V） ，求电阻R1，R2
消耗的功率，并分析功率关系。
·I2
+ uS(t)_
R1 5 R2 3 L 1H C 0.05F
+
2
解法二： 采用阻抗Z计算；
·IS
+ 1
U·
2 Z 2 (1 j)(2 j) 2 3 j
1 j 2 j
3
_ j1
-j1
3 j 1 ()
Z
•
U
ZIS
(3
3j 1)50 3
(15
j 5)(V ) 3
P IS 2 Re[Z ] 52 3 75(W )
3 32 (1/ 3)2
75(W )
Q UIS sin φ
152 (5 / 3)2 5
1/ 3 32 (1/ 3)2
8.3(Var)
S UIS 152 (5 / 3)2 5 75.5(VA) cos φ 0.993
第6章 正弦稳态电路分析
例：如图电路中，已知 is 5 2 sin 2（t A ），求电源提供的P、
+
U·S_
·I1
5
j5
3 -j4
解：U s 100V I1 2 45（ A） I2 253.1（ A）
P1 I12R1 （ 2）2 5 10（W）
或： P1 USI1 cos φ1=10 2 cos 45 10(W)
P2
I
2 2
R2
22
3
12（W）
或： P2 USI2 cos φ2=10 2 cos 53.1 12（W）
例：电路如图，已知 us (t) 10 2 sin 5（t V） ，求电阻R1，R2
消耗的功率，并分析功率关系。
·I2
+ uS(t)_
R1 5 R2 3 L 1H C 0.05F
+
正弦稳态交流电路相量的研究实验报告
正弦稳态交流电路相量的研究实验报告实验目的。
本实验旨在通过对正弦稳态交流电路相量的研究，探索交流电路中电压和电流的相量特性，加深对交流电路中相量概念的理解，并验证相关理论知识。
实验原理。
正弦稳态交流电路是指在电压和电流都是正弦波的情况下，电路中各个元件的电压和电流也是正弦波，并且频率相同、相位差不变。
在正弦稳态交流电路中，电压和电流的相量可以用复数表示，其中实部表示电压或电流的幅值，虚部表示相位差。
电压和电流的相量之间存在幅值比和相位差的关系。
实验仪器和材料。
1. 交流电源。
2. 电阻、电感、电容等元件。
3. 示波器。
4. 万用表。
5. 直流电源。
6. 信号发生器。
实验步骤。
1. 搭建正弦稳态交流电路，包括电压源、电阻、电感和电容等元件。
2. 连接示波器，观察电压和电流的波形，并测量其幅值和相位差。
3. 调节信号发生器的频率，观察电压和电流的波形随频率变化的规律。
4. 断开交流电源，接入直流电源，观察电压和电流的波形，并测量其幅值和相位差。
5. 记录实验数据，并进行数据处理和分析。
实验结果。
通过实验观测和数据处理，得出以下结论：1. 在正弦稳态交流电路中，电压和电流的相量可以用复数表示，实部表示幅值，虚部表示相位差。
2. 电压和电流的相量之间存在幅值比和相位差的关系，符合正弦函数规律。
3. 频率对电压和电流的相量有影响，频率增大时，电压和电流的相量幅值减小，相位差增大。
4. 在直流电源下，电压和电流的相量均为实数，相位差为零。
实验分析。
通过本实验的研究，加深了对正弦稳态交流电路中相量的理解，验证了相关理论知识。
实验结果表明，电压和电流的相量在交流电路中具有一定的规律性，频率对相量也有一定的影响。
这对于进一步研究交流电路、分析电路性能具有一定的指导意义。
结论。
本实验通过对正弦稳态交流电路相量的研究，验证了电压和电流的相量在交流电路中的特性，加深了对相量概念的理解。
同时，实验结果对于进一步研究交流电路、分析电路性能具有一定的指导意义。
第 4 节 正弦稳态电路的相量分析
第 4 节正弦稳态电路的相量分析相量分析法相量分析法是针对正弦量激励下、且电路已进入稳态时的动态电路的分析。
因为电路在正弦量的激励下，各处的响应都是同频率的正弦量，因此，将电路的激励和响应都用相量来表示，把电阻、电感、电容元件用复数阻抗或复数导纳表示，将电路定律用相量形式表示，把时域电路转换成相量电路之后，描述动态电路的方程就由时域中的微分方程转换为频域中的复数代数方程，求解复数代数方程，求得各响应的相量，然后再将这些响应的相量转换成时域的正弦函数表达式。
相量分析法的步骤正弦量用相量表示，电阻、电感、电容元件用阻抗或导纳表示，画出相量电路；2 、相量电路中，用电阻电路的分析方法求解各响应的相量；3 、将求得的响应相量转换成时域的正弦函数表达式。
例 7.4-1 电路如图 7.4-1 （ a ）所示，已知，求 uS ， iL 和 ic 。
解：电流 iR 的相量为感抗容抗所以，得到相量电路如图 7.4-1 （ b ）所示。
图 7.4-1 （ b ）中，有则由 KCL 得由 KVL 得将相量再转换成正弦函数表达式，得例 7.4-2 电路如图 7.4-2 所示，已知，，电压源的角频率，求电流 i1 和 i2 。
解：用节点电压法求解，设节点 a 、 b 的节点电压分别是和，列写节点电压方程，节点 a ：节点 b ：代入参数并整理，得则，所以，因此，，例 7.4-3 电路如图 7.4-3 所示，已知电压源，求电流。
解：这是一个含有受控源的单回路电路，用相量法分析时，也可将受控源当独立源处理。
由 KVL 得，代入参数，得则一、有功功率无源二端网络 N 中含有线性电阻、电容、电感、受控源等元件，阻抗为。
其端电压和端电流分别为。
二端网络 N 吸收的瞬时功率为平均功率（ average power ）是指在一个周期内吸收的瞬时功率的平均值，用 P 表示，即有功功率在一个周期内吸收的瞬时功率的平均值，称为平均功率，又称有功功率（ active power ），单位为瓦（ W ）。
第9章 正弦交流稳态电路分析
G 2R 2 , R X
B 2 X 2 R X
1 | Y | , φ y φz |Z|
注
一般情况 G1/R B1/X。若Z为感性， X>0，则B<0，即仍为感性。
同样，若由Y变为Z，则有：
R
Y
G
jB
Z
jX
Y G jB | Y | φ y ,
Z R jX | Z | φz
1 . U U R U L UC R I jL I j I C
.
.
.
.
.
.
U 1 Z R jL j R jX Z z I C
Z— 复阻抗；R—电阻(阻抗的实部)；X—电抗(阻抗的虚部)； |Z|—复阻抗的模；z —阻抗角。 转换关系：
例
L + + uR - + uL u C -
i
R
已知：R=15, L=0.3mH, C=0.2F,
u 5 2 cos(t 60 )
+ uC -
f 3 104 Hz . 求 i, uR , uL , uC .
.
解
其相量模型为：
I
R
.
j L
.
U 560 V
jL j2 3 104 0.3 103 j56.5Ω 1 1 j j j26.5Ω 4 6 C 2π 3 10 0.2 10 1 15 j56.5 j26.5 33.5463.4o Ω Z R j L j C
（1）C > 1/L ，B>0， y>0，电路为容性，电流超前电压 相量图：选电压为参考向量， u 0
正弦稳态电路的分析
B=|Y|sin '
I Y U i u
导纳三角形
|Y|
2019/2/26
B G
12/71
分析 R、L、C 并联电路得出：
（1）Y=G+j(C-1/L)=|Y|∠为复数，故称复导纳； （2）C > 1/L ，B>0， ‘>0，电路为容性，电流超前电压
C<1/L ，B<0， ‘<0，电路为感性，电流落后电压； C=1/L ，B=0， =0，电路为电阻性，电流与电压同相
2019/2/26
22/71
例5 已知：R1 1000 , R2 10 , L 500mH , C 10F ,
U 100V , 314rad / s , 求:各支路电流。
R1 i2 i1 i3 + _ u
I 1
C R2 L + U _
I 2
R1
j 1 C
k 1 k 1 n n
分流公式
Yi Ii I Y
两个阻抗Z1、Z2的并联等效阻抗为：
2019/2/26
Z1 Z 2 Z Z1 Z 2
18/71
例3 求图示电路的等效阻抗， ＝105rad/s 。 解 感抗和容抗为：
X L L 105 1 103 100
20/71
9. 3
正弦稳态电路的分析
正弦电路相量分析: KCL : I 0 KVL : U 0 元件约束关系: U Z I 或 I YU
电阻电路与正弦电流电路的分析比较：
电阻电路 : KCL : i 0 KVL : u 0 元件约束关系: u Ri 或 i Gu
I Y U i u
导纳三角形
|Y|
2019/2/26
B G
12/71
分析 R、L、C 并联电路得出：
（1）Y=G+j(C-1/L)=|Y|∠为复数，故称复导纳； （2）C > 1/L ，B>0， ‘>0，电路为容性，电流超前电压
C<1/L ，B<0， ‘<0，电路为感性，电流落后电压； C=1/L ，B=0， =0，电路为电阻性，电流与电压同相
2019/2/26
22/71
例5 已知：R1 1000 , R2 10 , L 500mH , C 10F ,
U 100V , 314rad / s , 求:各支路电流。
R1 i2 i1 i3 + _ u
I 1
C R2 L + U _
I 2
R1
j 1 C
k 1 k 1 n n
分流公式
Yi Ii I Y
两个阻抗Z1、Z2的并联等效阻抗为：
2019/2/26
Z1 Z 2 Z Z1 Z 2
18/71
例3 求图示电路的等效阻抗， ＝105rad/s 。 解 感抗和容抗为：
X L L 105 1 103 100
20/71
9. 3
正弦稳态电路的分析
正弦电路相量分析: KCL : I 0 KVL : U 0 元件约束关系: U Z I 或 I YU
电阻电路与正弦电流电路的分析比较：
电阻电路 : KCL : i 0 KVL : u 0 元件约束关系: u Ri 或 i Gu
第九章 正弦稳态电路的分析
依据上述数据，还可求出 依据上述数据，还可求出R1、L1： ：
& Us Z1 = = 38∠ 75 0 & I1 Z 1 = R 1 + j ωL 1 R 1 = 9.84 36.71 L1 = = 116.9mH 314
9-5
正弦稳态电路的功率 。 i u －。
＋
设一端口N内部不含独立源，仅有 、 、 设一端口 内部不含独立源，仅有R、L、C 内部不含独立源 吸收的功率： 吸收的功率：p=ui（关联方向） （关联方向） i = 2I cos(ωt + Ψi ) 设u = 2U cos(ωt + Ψu )
u
ϕ = Ψu − Ψi )
) − UIsin(-ϕ ) sin( 2ωt + 2Ψ ) = UI cos ϕ{1 + cos[2( ωt + Ψ ]} + UI sin ϕ sin[2(ωt + Ψ )]
u u
平均功率又称有功功率 一周期内的平均值 1T 1T p = ∫ pdt = ∫ UI[ cos ϕ + cos( 2ωt + Ψu + Ψi )]dt =UI cos ϕ T0 T0 功率因数 cosϕ用λ = cosϕ 无功功率 ϑ = UIsinϕ 视在功功率 S = UI
& 1 I I 导纳：阻抗Z的倒数定义为导纳 Y 的倒数定义为导纳： 导纳：阻抗 的倒数定义为导纳： = = = ∠ψ i − ψ u = Y ∠ϕ y & Z U U Y的代数式可写为： 的代数式可写为： 的代数式可写为 Y = G + jB ← 电纳 ↑ 电导 电阻YR =
单个元件的导纳： 单个元件的导纳：
单个元件的阻抗： 单个元件的阻抗：
第三章 正弦稳态电路分析
Ue j ψ U ψ 相量的模=正弦量的有效值 U
相量辐角=正弦量的初相角
电压的有效值相量
目录 上页 下页 返回
或：
U e jψ U ψ Um m m
相量的模=正弦量的最大值 相量辐角=正弦量的初相角
注意:
电压的幅值相量
① 相量只是表示正弦量，而不等于正弦量。
i Imsin(ω t ψ ) = Ime
储能 放能 储能 放能
目录 上页 下页 返回
无功功率 Q 用以衡量电感电路中能量交换的规模。用瞬时 功率达到的最大值表征，即
p 瞬时功率 ： i u UI sin 2 ω t
U2 Q U I I XL
2
XL
单位：var
目录 上页 下页 返回
3.3.3 电容元件伏安关系相量形式
时域形式：
已知 i(t ) 2I sin( t i )
R
I
uR (t ) Ri (t ) 2RI sin( t i ) UR u 相量形式： 有效值关系：UR=RI I I 则
i
+
UR
R
U R RI i
相量关系：
相位关系u= i (u,i同相) UR=RI
U 1 落后于U 2
U2
U2
45 20
U1
+1
超前 U ？ 落后 1
目录 上页 下页 返回
3.3 基尔霍夫定律的相量形式
电阻元件伏安关系相量形式
电感元件伏安关系相量形式 电容元件伏安关系相量形式
目录 上页 下页 返回
3.3.1 电阻元件伏安关系相量形式
i(t) + uR(t)
电路第五版课件 第九章正弦稳态电路分析
. IL
2017年2月9日星期四
. U
16
9.1.3 阻抗（导纳）的串联和并联
1.阻抗的串联 . . . . U = Z1 I + Z2 I + · · · + Zn I . = (Z1+ Z2 + · · · + Zn) I . = ZI
Z=
n . I Z1 Z2 Zn
+ . U . I
k
∑ Z = ∑ (R + j X )
. I2 Y2
. In Yn
∑ Y = ∑ (G + j B )
k=1
k k
k=1
分流公式
Z1 Z2 两个阻抗Z1、Z2的并联等效阻抗为：Z = Z1 + Z2
2017年2月9日星期四 18
. Yk . Ik = I Y
+ . U -
Y
例：如图所示电路，已知R=10Ω, XL=10 Ω , XC=10 Ω, 求ab两端的等效阻抗Z；电压相量与电流相量相位差
2017年2月9日星期四 7
. . U = R + j X= | Z | j jwL R Z= . Z I . . I + + UR - + UL 1 X = XL - XC = wL. + . wC U UC X jZ = arctan R 讨论： 1 时， ①当 wL＞ wC 有 X＞0 ，jZ＞0
. UL
1 jwC
以电流为参考相量的相量图
. . UL + UC
. U
表现为电压超前电流，Z 呈感 性，称电路为感性电路。 满足：U 2 =UR2 + (UL-UC)2
2017年2月9日星期四
2017年2月9日星期四
. U
16
9.1.3 阻抗（导纳）的串联和并联
1.阻抗的串联 . . . . U = Z1 I + Z2 I + · · · + Zn I . = (Z1+ Z2 + · · · + Zn) I . = ZI
Z=
n . I Z1 Z2 Zn
+ . U . I
k
∑ Z = ∑ (R + j X )
. I2 Y2
. In Yn
∑ Y = ∑ (G + j B )
k=1
k k
k=1
分流公式
Z1 Z2 两个阻抗Z1、Z2的并联等效阻抗为：Z = Z1 + Z2
2017年2月9日星期四 18
. Yk . Ik = I Y
+ . U -
Y
例：如图所示电路，已知R=10Ω, XL=10 Ω , XC=10 Ω, 求ab两端的等效阻抗Z；电压相量与电流相量相位差
2017年2月9日星期四 7
. . U = R + j X= | Z | j jwL R Z= . Z I . . I + + UR - + UL 1 X = XL - XC = wL. + . wC U UC X jZ = arctan R 讨论： 1 时， ①当 wL＞ wC 有 X＞0 ，jZ＞0
. UL
1 jwC
以电流为参考相量的相量图
. . UL + UC
. U
表现为电压超前电流，Z 呈感 性，称电路为感性电路。 满足：U 2 =UR2 + (UL-UC)2
2017年2月9日星期四
正弦交流电电路稳态分析
分析含有非线性元件的交流电路中电压、电流和功率的分布和计算。
详细描述
含有非线性元件的交流电路是指包含非线性电阻、非线性电感和非线性电容等元件的交流电路。在稳态分析中， 需要采用适当的数学方法来计算各元件的电压、电流和功率，并确定它们在含有非线性元件的交流电路中的分布 情况。
含有非线性元件的交流电路稳态分析
正弦交流电电路稳态分析
目 录
• 引言 • 正弦交流电基础知识 • 电路稳态分析方法 • 正弦交流电电路稳态分析实例 • 结论与展望
01 引言
背景介绍
正弦交流电的产生
交流发电机利用电磁感应原理将机械能转换为电能。当转子 绕组中的电流随时间变化时，就会产生旋转磁场，该磁场会 与定子绕组中的感应电流相互作用，从而产生正弦交流电。
02 03
详细描述
三相交流电路是指电源和负载之间的电压和电流在三个相位上变化的电 路。在稳态分析中，需要计算各相的电压、电流和功率，并确定它们在 三相电路中的分布情况。
总结词
考虑三相阻抗、三相感抗和三相容抗对电路的影响。
三相交流电路稳态分析
• 详细描述：在三相交流电路中，三相阻抗、三相感抗和三相容 抗是影响各相电压和电流分布的重要因素。三相阻抗包括电阻、 电感和电容在三相电路中的作用，而三相感抗和三相容抗则是 由于电感和电容产生的磁场和电场对电流的阻碍作用。
解决实际工程问题
在实际的电力系统和电子设备中，正弦交流电的应用非常广泛。因此，对正弦交流电电路 稳态分析的研究有助于解决实际工程问题，提高电力系统和电子设备的性能和稳定性。
推动相关领域的发展
正弦交流电电路稳态分析涉及到多个学科领域，如电路理论、电磁场理论、控制系统理论 等。因此，对正弦交流电电路稳态分析的研究有助于推动相关领域的发展，促进多学科交 叉融合。
详细描述
含有非线性元件的交流电路是指包含非线性电阻、非线性电感和非线性电容等元件的交流电路。在稳态分析中， 需要采用适当的数学方法来计算各元件的电压、电流和功率，并确定它们在含有非线性元件的交流电路中的分布 情况。
含有非线性元件的交流电路稳态分析
正弦交流电电路稳态分析
目 录
• 引言 • 正弦交流电基础知识 • 电路稳态分析方法 • 正弦交流电电路稳态分析实例 • 结论与展望
01 引言
背景介绍
正弦交流电的产生
交流发电机利用电磁感应原理将机械能转换为电能。当转子 绕组中的电流随时间变化时，就会产生旋转磁场，该磁场会 与定子绕组中的感应电流相互作用，从而产生正弦交流电。
02 03
详细描述
三相交流电路是指电源和负载之间的电压和电流在三个相位上变化的电 路。在稳态分析中，需要计算各相的电压、电流和功率，并确定它们在 三相电路中的分布情况。
总结词
考虑三相阻抗、三相感抗和三相容抗对电路的影响。
三相交流电路稳态分析
• 详细描述：在三相交流电路中，三相阻抗、三相感抗和三相容 抗是影响各相电压和电流分布的重要因素。三相阻抗包括电阻、 电感和电容在三相电路中的作用，而三相感抗和三相容抗则是 由于电感和电容产生的磁场和电场对电流的阻碍作用。
解决实际工程问题
在实际的电力系统和电子设备中，正弦交流电的应用非常广泛。因此，对正弦交流电电路 稳态分析的研究有助于解决实际工程问题，提高电力系统和电子设备的性能和稳定性。
推动相关领域的发展
正弦交流电电路稳态分析涉及到多个学科领域，如电路理论、电磁场理论、控制系统理论 等。因此，对正弦交流电电路稳态分析的研究有助于推动相关领域的发展，促进多学科交 叉融合。
第九章正弦稳态电路分析
重点
2
难点
复阻抗和复导纳的概念； 直流电路的分析方法及定理在正弦稳态电 路分析中的应用； 正弦稳态电路中的功率与能量关系，如平 均功率、无功功率、视在功率、复功率、 功率因数的概念及计算； 应用相量图分析电路的方法。 本章与其它章节的联系
直流电路的分析 + 相量法基础 → 正弦稳态电路 的分析方法，在第10、11、12章节中都要用到。
N0
6
jwL R (4)RLC串联电路 . - + . + 根据KVL和VCR的 + U UL R . .+ 相量形式可得： U UC . . . 1 . U = R I + jwL I - j I wC 1 . = [R + j(X +X )] . = R + jwL- j I L C I wC . . = (R + jX) I = Z I . U =R+jX=|Z| j Z= . z I X 1 jz = arctg X = XL + XC = wLR wC . I
所以 Y = 0.2 -30o S
17
若已知 Z=R+jX ，求等效的 Y=G+jB (R - jX) 1 = 1 = 则： = Y Z R + jX (R + jX) (R - jX) -X = G + jB R = 2 2 +j 2 2 R +X R +X R X G= 2 B=- 2 |Z| |Z|
4
(2)阻抗参数间的关系
指数式：Z=| Z | e
jj z
极坐标式：Z = | Z | jz
+ . U -
第9章正弦稳态电路分析
ϕz
R
X
(3)单个元件的阻抗 单个元件的阻抗 + . . . I U =R 纯电阻 Z = . U R I N0 − . U = jωL = j X 纯电感 Z = . L + . I I . L U XL=ωL 称感性电抗，XL ∝ f ！ 性电抗 . N0 U 1 = −j 1 = j X − 纯电容 Z = . = C ωC jωC + . I 1 称容性电抗，X ∝ (1/f ) ！ . I XC = − 性电抗 C C U ωC 可以是纯实数， 说明 Z 可以是纯实数， 也可以是纯虚数。 也可以是纯虚数。
C
. U = R + j X= | Z | ϕ Z= . z I X = XL + XC = ωL− 1 − ωC ϕz = arctg X R
. I + U
.
. . + U − + UL − .+ R
. UX UC −
ቤተ መጻሕፍቲ ባይዱ
R
jωL 1 jωC N0
−
④当R=0，X >0时，Z 为纯电感性； 为纯电感性； = ， 时 为纯电容性。 ⑤当R=0，X<0时，Z 为纯电容性。 = ， 时 RLC 串联电路的电压 UR、 UX、U 构成电压三角形。 构成电压三角形。 |Z| 满足： 满足： = U
§9−1 阻抗和导纳 −
1. 阻抗 阻抗Z (1)定义 定义
. + I . U − 含线性 无源元 件的一 端口N 端口 0
. . I = I φi 设：U = U φu . def U = U φ −φ = | Z | ϕz u i 则：Z . I I | Z | = U 为阻抗的模，也可以简称为阻抗。 阻抗的模，也可以简称为阻抗 阻抗。 I ϕz =φu−φi 为阻抗角。 阻抗角。 ϕz就是该阻抗两端的 电压与通过该阻抗电 阻抗的单位与 流的相位差ϕ ！ 电阻相同。 电阻相同。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第九章 正弦稳态电路的分析第一节用相量法分析R 、L 、C 串联电路 — 阻抗一、R 、L 、C 串联电路中电流与电压的大小、相位关系： 电路如图9-1-1。
设)t (ISin 2)t (Sin I i i i m ϕ+ω=ϕ+ω=则电路中各元件的电压及总电压均为与电流同频率的正弦量。
由KVL ，C L R u u u u ++=用相量表示：其中： )(IUI U IUZ z Rx tg x R jx R )x x j R C 1L j R Z i u i u ..122C L ϕ-ϕ∠=ϕ∠ϕ∠==ϕ∠=∠+=+=-+=ω-ω+=-或（）（z 称为阻抗的模，ϕ称为阻抗的幅角，由于阻抗本身不是正弦量，是一个纯复数，因此不用“.” 表示。
ϕ又称为阻抗角。
复阻抗与元件的参数和激励的角频率有关，而与电压、电流相量无关，阻抗角是由于储能元件L 、C 造成的。
当00x x 0x x 0x i u C L C L >ϕ-ϕ>ϕ>>->，时即，电压超前电流一个角度ϕ,电路为感性；当00x x 0x x 0x i u C L C L <ϕ-ϕ<ϕ<<-<，时即，电压滞后电流一个角度ϕ,电路为容性。
当，，，0x x 0x C L =ϕ==则电压、电流同相，电路发生串联谐振。
由以上关系： )(zI I z I Z U i i ..ϕ+ϕ∠=ϕ∠ϕ∠== 总电压)t (USin 2)t (zISin 2u u i ϕ+ω=ϕ+ϕ+ω=即间的关系。
为电压、电流有效值之可正可负；，,zI U i u =ϕϕ+ϕ=ϕ 二、R 、L 、C 串联电路的相量图。
为了方便，以感性电路（ϕ>0）为例，如图9-1-2。
......C .L .R ..IZ I ]C1L j R [I C 1j I L j I R U C L R U U U U =ω-ω+=ω-ω+=++=）（量关系表达式的电压、电流之间的相、、带入)20t 314(Sin 2202u ︒+=在相量上，表明各个相量之间的相位关系非常重要，在指定电流的初相角的情况下，可按给定的初相角画出其相量，若在题目中只给定了电流的有效值，而没有给定初相角的情况下，可设电流为参考正弦量，令其初相角为0，其它相量可根据与参考正弦量的关系得到。
在串联电路中，以电流I 为参考正弦量较方便。
如图9-1-3，9-1-4。
由以上分析可以看出：三个电压的有效值之间形成直角三角形的关系—电压三角形，故若将电压三角形三边分除以I ，得到阻抗三角形。
如图9-1-5。
从电压三角形可以看出：【实例9-1】一个实际的电感线圈具有电阻R=30Ω，L=127mh ，与电容器C=40μF 串联后接至电压 的电源上。
如图例9-1。
求：①复阻抗，电流的有效值、相量、瞬时值。
②电容和线圈上电压的瞬时值。
③作电压、电流相量图。
【解】XR 2C L 2R 2X 2R U U U )U U (U U U U +≠-+=+=一般情况下9.163521.734.4*80j I c1j U )2()1.73t 314(Sin 4.42i :A4.4I 1.734.41.535020220Z U I 80j Z 1.5350314j 30Z 1.535040j 3080j 40j 3010*40*3141j 10*127*314j 30Z Z )C 1L (j R Z )1(.C ...C RL 63C RL ︒-∠=︒∠-=ω-=︒+==︒∠=︒∠︒∠==Ω-=Ω︒-∠=+=Ω︒∠=-=-+=-+=+=ω-ω+=--瞬时值表达式为其中有效值电流，其中阻抗相量图如9-1-6。
第二节 用相量法分析R 、L 、C 并联电路 — 导纳一、R 、L 、C 并联电路中电流与电压的大小、相位关系： 电路如图9-1-7。
设)t (USin 2)t (Sin U u u i m ϕ+ω=ϕ+ω=则电路中各元件的电流及总电流均为与电压同频率的正弦量。
由KCL ，当B>0时，电路为容性，B<0时，电路为感性，B=0电路发生并联谐振。
二、相量图：如图9-2-2为一般情况下，感性电路各电压、电流之间的关系。
图9-2-3是以电压为参考正弦量时，感性电路、容性电路的相量图。
称为复导纳。
式中)(y y jB G )]B B (j G [Y UY U )]B B (j G [U jB U jB U G U C j L j UR U I I I I u i C L ..C L .C .L ....C.L .R ..ϕ-ϕ-∠=ϕ-∠=-=--==--=+-=ω+ω+=++=。
，可见或即或R 1G G 1R B G B X B G G R X R X B X R R G X R jX R jX R 1B G Y Y1Z Z 1Y 2222222222≠≠⎪⎪⎩⎪⎪⎨⎧+=+=⎪⎪⎩⎪⎪⎨⎧+=+=⇒+-=+=-===（感性）。
，即并联等效电路参数为：（感性）。
，即串联等效电路参数为：，）解：电路。
求：其串联、并联等效已知：S 1.0B S 31.0G 1.0j 31.0302.0UI Y 5.2X 35.2R 5.2j 35.2305IUZ 6022I 90210U 60t 10(Sin 2)30t 10(Cos 2i A)30t 10(Cos 2i V)90t 10(Sin 10u ......==-=︒-∠==Ω=Ω=+=︒∠==︒∠=︒∠=︒+=︒-=︒-=︒+=由相量图可见：三、复阻抗与复导纳的等值转换：任意无源一端口网络可以用一等值阻抗或等值导纳来描述。
如图9-1-10。
因此复阻抗与复导纳之间等效转换的关系为：【实例9-2】电路如图例9-2。
CL R 2C L 2R I I I I )I I (I I ++≠-+=一般情况下，解之得：）（）（整理）（452U 4522U j U j 1U j 1j 1U j U U U j R 1j 1U j 1j 01U j 1U )j 1j 1(U ...2n .1n .2n .1n .2n .1n .1.1.1n .2n .1n .1n .︒∠=︒∠=⎪⎩⎪⎨⎧=++---=-⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=+-+---︒∠=---+第三节 正弦交流电路的计算直流电路中以KCL 、KVL 为基础的方法和定理完全适用于正弦交流电路，不同的是电压、电流为相量，电阻变为阻抗，在复杂电路中还可以借助于相量图进行分析，特别在定性分析中尤为重要。
一、阻抗串联：1、复阻抗的计算：Z=Z 1+Z 2+…+Z n2、分压公式：二、阻抗（导纳）并联：1、 复导纳的计算：Y=Y 1+Y 2+…+Y n2、 分流公式：三、复杂连接：通过例题介绍。
【实例9-3】已知：R 1=5Ω，X C1=5Ω，X C2=10Ω，X L2=20Ω，X L3=10Ω。
求：电路的总阻抗Zab ，并说明电路的性质。
【解】根据阻抗的串、并联计算公式：【实例9-4】如图例9-4。
【解】利用结点电压法，方程及结果如下。
为分压系数。
阻抗为正比分压，其中n21Kn 21K .ZK .Z ...Z Z Z Z ...Z Z Z UU ++++=为分流系数。
导纳为正比分流，其中n21Kn 21K .GK .G ...G G G G ...G G G II ++++=。
，电路表现为电阻性质Ω=++-=510j 10j 10j *10j 5j 5Z ab 的瞬时值表达式。
电流相量。
电流求：。
，，，，已知：C C .C L 2S .1S .i )2(I )1(1R j jx j jx A 901I A 01I Ω=Ω-=-Ω=︒-∠=︒∠=3129j 13739.663500035U Z 9.6601.0I 0350035.0*1000I R U 9.663908.001.0*035.0*201.0035.00.04I I 2I I I Cos Cos I I 2I I )180(Cos I I 2I I Cos I I 2I I I ..RL 2.1.1.22221222122122212122212122212+=︒∠=︒∠==︒-∠=∴︒∠=︒∠==︒=θ⇒=--=--=θ∴θ++=θ-︒-+=ϕ-+=而根据相量图。
【实例9-5】图例9-5是一个RC 移相电路，要使输出电压与输入电压之间产生180度的相位移。
求：电源信号的角频率与电路参数之间的关系，并求在此频率下电路的电压传输系数。
【解】本题可有多种解题方法，但基本的是回路电流法，选择回路电流为独立变量，如图例9-4。
【实例9-6】为测量某电感线圈的参数R 、L ，可用一只安培表和一个已知电阻R1，组成电路图9-6。
设R 1=1K ，I=0.04A ，I 1=0.035A,I 2=0.01A ，若电源为工频，求：线圈的参数R ，L 。
，结果同上。
即分子为或则零，即相，令表达式的虚部为为使输出、输入电压反）（）（，所以而）（解得：0180RC 51RC 1CR 6tg RC 610RC 1CR 6)R C 1CR 6(j R C 511)C 1C R 6(j C R 5R R U U I R U )]C1C R 6(j C R 5R [U R I 0I )C 1j R 2(I R 0I R I )C 1j R 2(I R U I R I )C 1j R (222333133333322233222331.2.3.2.3322231.23.3.2.3.2.1.1.2.1.︒=ω-ω-ω=ϕ=ω=ω-ωω-ω-ω-=ω-ω-ω-==ω-ω-ω-=⎪⎪⎪⎩⎪⎪⎪⎨⎧=ω-+-=-ω-+-=-ω--的大小。
可算出，即可求出即为阻抗角，而间相位差，、一个角度，只要找出滞后于电压电流。
，则为参考正弦量，即分析：以电压RL ..2..2.1...Z U U I U I 0035.0I 0U U U ︒∠=︒∠=这就是三电流表法测未知阻抗的原理。
第四节 正弦交流电路的功率在正弦交流电路中，由于电阻、电感、电容的存在，使得功率的计算比直流电路复杂 得多，既有能量的消耗，又有能量的往返交换。
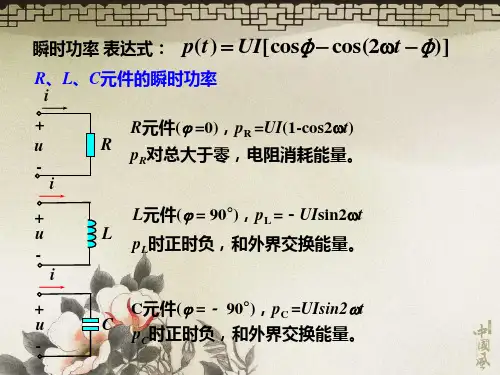
一、瞬时功率：如图9-4-1（以感性电路为例）。
当p>0时，此二端网络吸收功率，p<0时发出功率。
二、平均功率（有功功率）和功率因数：- 根据数学中平均值的定义，三、无功功率和无功因数：无功功率是这样定义的。
根据瞬时功率的表达式四、视在功率：视在功率定义为S=UI 。
计量单位为“伏-安”、“千伏-安“（V A 、KV A ）。
一般用来表示发电设备的容量。
在数值上等于最大的有功功率。
五、S 、P 、Q 之间的关系：【实例9-7】三表法测未知参数的电路如图例9-7。