信号检测与估计 第五章 答案

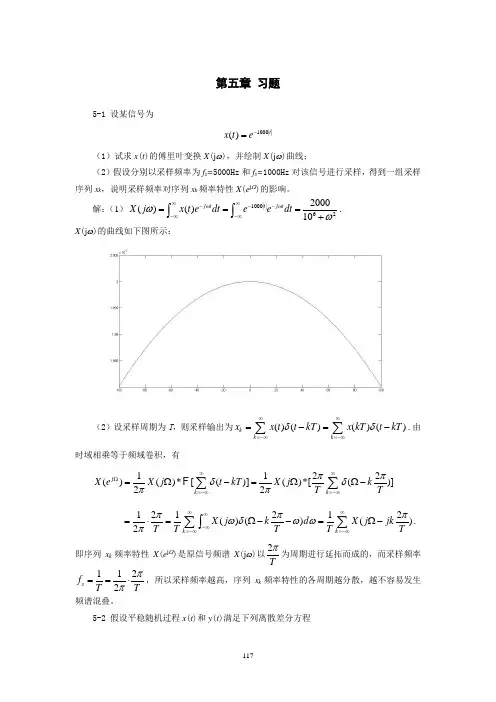
第五章 习题5-1 设某信号为1000||()t x t e -=（1）试求x (t )的傅里叶变换X (j ω)，并绘制X (j ω)曲线；（2）假设分别以采样频率为f s =5000Hz 和f s =1000Hz 对该信号进行采样，得到一组采样序列x k ，说明采样频率对序列x k 频率特性X (e j Ω)的影响。

解：（1）1000||622000()()10j t t j t X j x t e dt e e dt ωωωω∞∞----∞-∞===+⎰⎰. X (j ω)的曲线如下图所示：（2）设采样周期为T ，则采样输出为()()()()k k k x x t t kT x kT t kT δδ∞∞=-∞=-∞=-=-∑∑.由时域相乘等于频域卷积，有1122()()*[()]()*[()]22j k k X e X j t kT X j kT Tππδδππ∞∞Ω=-∞=-∞=Ω-=ΩΩ-∑∑F 121212()()()2k k X j k d X j jk T T T T Tπππωδωωπ∞∞∞-∞=-∞=-∞=⋅=Ω--=Ω-∑∑⎰. 即序列x k 频率特性X (e j Ω)是原信号频谱X (j ω)以2Tπ为周期进行延拓而成的，而采样频率1122s f T Tππ==⋅，所以采样频率越高，序列x k 频率特性的各周期越分散，越不容易发生频谱混叠。

5-2 假设平稳随机过程x (t )和y (t )满足下列离散差分方程11;k k k k k k k x ax e y ay x v ---=-=+式中，|a|<1；e k ，v k ～N (0，σ 2)分布，且二者互不相关。

试求随机序列y k 的功率谱。

解：对1k k k x ax e --=进行离散时间傅里叶变换（DTFT ），且记DTFT(x k )=X (e j Ω)，DTFT(e k )=E (e j Ω)，则有j j j ()(1)()X e ae E e ΩΩΩ--=式中，Ω=ωT s ，称为数字频率（rad ），ω为实际频率（rad/s ），T s 为采样周期（s ）。

一、填空题说明填空题（每空1分，共10分）或（每空2分，共20分）二、第1章填空题1．从系统的角度看，信号检测与估计的研究对象是 加性噪声情况信息传输系统中的接收设备 。

从信号的角度看，信号检测与估计的研究对象是 随机信号或随机过程 。

2．信号检测与估计的基本任务：以数理统计为工具，解决接收端信号与数据处理中 信息恢复与获取 问题。

3．信号检测与估计的基本任务：以数理统计为工具，从被噪声及其他干扰污染的信号中 提取、恢复 所需的信息。

4．信号检测是在噪声环境中，判断 信号是否存在或哪种信号存在 。

信号检测分为 参量检测和 非参量检测 。

参量检测是以 信道噪声概率密度已知 为前提的信号检测。

非参量检测是在 信道噪声概率密度为未知 情况下的信号检测。

5．信号估计是在噪声环境中，对 信号的参量或波形 进行估计。

信号估计分为 信号参量估计和 信号波形估计 。

信号参量估计是对 信号所包含的参量（或信息） 进行的估计。

信号波形估计是对 信号波形 进行的估计。

6．信号检测与估计的数学基础：数理统计中贝叶斯统计的 贝叶斯统计决策理论和方法 。

三、第2章填空题1．匹配滤波器是在输入为 确定信号加平稳噪声 的情况下，使 输出信噪比达到最大 的线性系统。

2．匹配滤波的目的是从含有噪声的接收信号中，尽可能 抑制噪声，提高信噪比 。

3．匹配滤波器的作用：一是使滤波器 输出有用信号成分尽可能强 ；二是 抑制噪声，使滤波器输出噪声成分尽可能小 。

4．匹配滤波器的传输函数与输入 确定信号频谱的复共轭 成正比，与输入 平稳噪声的功率谱密度 成反比。

3．匹配滤波器传输函数的幅频特性与输入 确定信号的幅频特性成 正比，与输入 平稳噪声的功率谱密度 成反比。

4．物理不可实现滤波器也称作非因果滤波器：是指 物理上不可能实现或不满足因果规律 的滤波器。

5．物理不可实现匹配滤波器的冲激响应)(t h 满足： 0)(≠t h ， ∞<<∞-t 。

《信号检测与估计》第五章习题解答5.1 考虑检测问题：()()()T t t n t B t x H ≤≤++=0cos 20φω：()()()T t t n t B t A t x H ≤≤+++=0cos cos 211φωω：其中A 、B 、1ω和2ω为已知常数。

()t n 是高斯白噪声，φ在()π20，上服从均匀分布。

（a ）求判决公式及最佳接收机结构形式。

（b ）如果0sin cos cos cos 021021==∫∫T T tdt t tdt t ωωωω，证明最佳接收机可用()∫Tdt t t x 01cos ω作为检测统计量并对此加以讨论。

解：设()t n 为均值为零、功率谱密度为2/0N 的高斯白噪声，可得()()()()∫+−−=T dt t B t x N FeH x f 0220cos 10,φωφ ()()()()∫+−−−=T dt t B t A t x N FeH x f 02210cos cos 11,φωωφ得到()()()()()()()()dt t t N AB dt t N A dt t t x N A dt t B t A t x t N A T T T T ee e e H xf H x f x l φωωωωφωωωφφφ+−+−−−∫∫∫∫===20100120201021010cos cos 2cos cos 2cos 2cos 2cos 01,, 由于φ在()π20，上服从均匀分布，得到()⎪⎩⎪⎨⎧≤≤=其他02021πφπφf()()()()()φπφφφπφωωωωπd e e e d f x l x l dt t t N AB dt t N A dt t t x N A T T T ∫∫+−∫∫∫==20cos cos 2cos cos 22020100120201021根据Bayes 准则可得()010l x l H H >< ()()020cos cos 2cos cos 21020100120201021l d e e e H H dt t t N AB dt t N A dt t t x N A T T T ><+−∫∫∫∫φππφωωωω ()()dt t t x N A l d e dt t N A T H H dt t t N AB T T ∫−+∫><+∫∫010020cos cos 201202cos 22ln ln cos 102010ωπφωπφωω ()()dt t t x l A N d e A N dt t A T H H dt t t N AB T T ∫−+∫><+∫∫010020cos cos 20012cos 2ln 2ln 2cos 2102010ωπφωπφωω 5.2 假定上题中i A 的概率密度函数是()()()2022201A A i i i i e A A p A p A f −+−=δ求似然比及其在0A 趋于零时的形式。

电子科技大学：何子述、孔令讲第五章波形估计电子科技大学：何子述、孔令讲5、1 引言本章习题：1、2、8参数估计：12{,,,}M αααα= 不随时间变化。

波形估计：随时间变化的信号s(t)，对s(t)进行估计。

等效于对时变参量的估计。

可用参量化估计：贝叶斯估计、MAP 、ML 等，前提：须知概率分布。

电子科技大学：何子述、孔令讲0()()()()y t x t g t s t t =∗⎯⎯⎯→+逼近()()()x t s t n t =+实际中常用线性估计。

选择g(t)，使y(t)在某种意义下逼近s(t+t 0)。

常用最小均方误差MMSE 准则。

2:()()()[()]m inlet e t s t s t E e t =−→ 使电子科技大学：何子述、孔令讲估计量为s(t+t 0)，根据不同的应用要求，t 0取值不同。

（1）若t 0=0，即估计当前时刻值，s(t)，称为滤波（Filtering）（2）若t 0>0，即估计未来时刻值，s(t+t 0)，称为预测（Prediction）；如：拦截导弹。

（3）若t 0<0，估计过去s(t+t 0)，称为平滑（Smoothing）；电子科技大学：何子述、孔令讲5、2 维纳（Wiener ）滤波理论1、Wiener滤波设期望信号：d(t)=s(t+t 0)；接收信号：x(t)=s(t)+n(t);构造线性滤波器：冲激响应为g(t)，输出为y(t)()()()()()y t g t x t g x t d τττ+∞−∞=∗=−∫目的：选择g(t)，使y(t) d(t)电子科技大学：何子述、孔令讲5、2 维纳（Wiener ）滤波理论∵n(t)：随机过程→x(t)，故y(t)是随机过程。

因此只能在统计意义下使y(t) →d(t):准则：误差的平均功率→min22[()][()()]minE e t E d t y t =−→电子科技大学：何子述、孔令讲0200()()()()[()]{[()()()][()()()]*}e t s t t g x t d E e t E s t t g x t d s t t g r x t r dr ττττττ+∞−∞+∞−∞+∞−∞=+−−∴=+−−×+−−∫∫∫∵若s(t)是实的，20[()](0)2()()()()()]s xs x E e t R g R t d g r g R r d dr ττττττ+∞−∞+∞+∞−∞−∞=−++−∫∫∫()[()*()]()[()*()]s xs R E s t s t R E x t s t ττττ=−=−（5-9）电子科技大学：何子述、孔令讲选择g(t)，使2[()]minE e t →可用变分法得：0[()()()]0()xs x R t g u R u du d ηττττ+∞+∞−∞−∞−++−=∫∫()t η为扰动函数，要求为连续可导的任意函数2、g(t)的求解（1）g(t)为非因果信号，-∞<t<+∞,物理上不可实现。

信号检测及估计试题-答案（不完整版）一、概念：1. 匹配滤波器。

概念：所谓匹配滤波器是指输出判决时刻信噪比最大的最佳线性滤波器。

应用：在数字信号检测和雷达信号的检测中具有特别重要的意义。

在输出信噪比最大准则下设计一个线性滤波器是具有实际意义的。

2. 卡尔曼滤波工作原理及其基本公式(百度百科)首先，我们先要引入一个离散控制过程的系统。

该系统可用一个线性随机微分方程（Linear Stochastic Difference equation）来描述：X(k)=A X(k-1)+B U(k)+W(k)再加上系统的测量值：Z(k)=H X(k)+V(k)上两式子中，X(k)是k时刻的系统状态，U(k)是k时刻对系统的控制量。

A和B是系统参数，对于多模型系统，他们为矩阵。

Z(k)是k时刻的测量值，H是测量系统的参数，对于多测量系统，H为矩阵。

W(k)和V(k)分别表示过程和测量的噪声。

他们被假设成高斯白噪声(White Gaussian Noise)，他们的covariance 分别是Q，R（这里我们假设他们不随系统状态变化而变化）。

对于满足上面的条件(线性随机微分系统，过程和测量都是高斯白噪声)，卡尔曼滤波器是最优的信息处理器。

下面我们来用他们结合他们的covariances 来估算系统的最优化输出（类似上一节那个温度的例子）。

首先我们要利用系统的过程模型，来预测下一状态的系统。

假设现在的系统状态是k，根据系统的模型，可以基于系统的上一状态而预测出现在状态：X(k|k-1)=A X(k-1|k-1)+B U(k) (1)式(1)中，X(k|k-1)是利用上一状态预测的结果，X(k-1|k-1)是上一状态最优的结果，U(k)为现在状态的控制量，如果没有控制量，它可以为0。

到现在为止，我们的系统结果已经更新了，可是，对应于X(k|k-1)的covariance还没更新。

我们用P表示covariance：P(k|k-1)=A P(k-1|k-1) A’+Q (2)式(2)中，P(k|k-1)是X(k|k-1)对应的covariance，P(k-1|k-1)是X(k-1|k-1)对应的covariance，A’表示A的转置矩阵，Q是系统过程的covariance。

一、简答题注释简答题（每题5分，共20分）或（每题4分，共20分）二、第1章简答题1．从系统和信号的角度看，简述信号检测与估计的研究对象。

答：从系统的角度看，信号检测与估计的研究对象是加性噪声情况信息传输系统中的接收设备。

从信号的角度看，信号检测与估计的研究对象是随机信号或随机过程。

2．简述信号检测与估计的基本任务和所依赖的数学基础。

答：解决信息传输系统接收端信号与数据处理中信息恢复与获取问题，或从被噪声及其他干扰污染的信号中提取、恢复所需的信息。

信号检测与估计所依赖的数学基础是数理统计中贝叶斯统计的贝叶斯统计决策理论和方法。

3．概述信号在传输过程中与噪声混叠在一起的类型。

答：信号在传输过程中，噪声与信号混杂在一起的类型有3种：噪声与信号相加，噪声与信号相乘（衰落效应），噪声与信号卷积（多径效应）。

与信号相加的噪声称为加性噪声，与信号相乘的噪声称为乘性噪声，与信号卷积的噪声称为卷积噪声。

加性噪声是最常见的干扰类型，也是最基本的，因为乘性噪声和卷积噪声的情况均可转换为加性噪声的情况。

三、第2章简答题1．简述匹配滤波器概念及其作用。

答：匹配滤波器是在输入为确定信号加平稳噪声的情况下，使输出信噪比达到最大的线性系统。

匹配滤波器的作用：一是使滤波器输出有用信号成分尽可能强；二是抑制噪声，使滤波器输出噪声成分尽可能小，减小噪声对信号处理的影响。

2．根据匹配滤波器传输函数与输入确定信号及噪声的关系，简述匹配滤波器的原理。

答：匹配滤波器传输函数等于输入确定信号频谱的复共轭除以输入平稳噪声的功率谱密度，再附加相位项T ω-，其中T 为输入确定信号的持续时间或观测时间。

由于匹配滤波器传输函数的幅频特性与输入确定信号的幅频特性成正比，与输入噪声的功率谱密度成反比；对于某个频率点，信号越强，该频率点的加权系数越大，噪声越强，加权越小。

从而起到加强信号，抑制噪声的作用。

对于信号，匹配滤波器的相频特性与输入信号的相位谱互补，使输入信号经过匹配滤波器以后，相位谱将全部被补偿掉。

5-1 用冲击响应不变法求相应的数字滤波器系统函数H(z)1）H a (s) =2332+++s s s 2）H a (s) = 4212+++s s s解：由H a (s)分解成部分分式之和 1）H a (s) =2332+++s s s =)1)(2(3+++s s s =12+s –21+s∴H(z) = 112---z e T –1211---z e T =2311)1(1)21(1--------++--+ze z e e z e e T T T T T 2）H a (s) =4212+++s s s =3221πjes ++3221πjes -+∴H(z) =123121---z e jTe π+123121----z e jTeπ=2211)3cos(21)3cos(1------+--ze z T e z T e TTT5-2 设h a (t)表示一个模拟滤波器的单位冲击响应 te9.0- , t ≥0h a (t)=0 , t ＜0（1）用冲击响应不变法，将此模拟滤波器转换成数字滤波器，确定系统函数H(z)（以T 作为参数）（2）证明，T 为任何值时，数字滤波器是稳定的，并说明数字滤波器近似为低通滤波器，还是高通滤波器解：（1）∵ h a (t)= te9.0-u(t)∴ H a (s) =9.01+s ∴ H(z) =19.011---ze T (2)∵ H(z) =19.011---ze T则其极点为z=Te9.0-∵ T > 0 ∴ |z | < 1H(ωj e ) =ωj e z z H =|)( = Tj j e e e9.0--ωω可以看出当ω↑时，| H(ωj e ) |↓ ∴ 是低通滤波5-3 图5-40是由RC 组成的模拟滤波器，写出其系统函数H a (s)，并选用一种合适的转换方法，将H a (s)转换成数字滤波器H(z) 解：由回路法可知（这是一个高通滤波器） y a (t)=dt t dU RC c )(= dt t dx RC a )(–dtt dy RC a )( ∴)()(s X s Y =RCsRCs +1= H a (s) 由于脉冲响应不变法只适宜于实现带通滤波器，所以最好用双线性变换法实现H(z)∴H(z) =11112|)(--+-⋅=z z T s a s H =11111121112----+-⋅++-⋅z z T RC z z T RC =211)2()2()1(2-----++-z z RC T RC T z RCx a (t)CRy a (t)5-4 设模拟滤波器的系统函数为H a (s)= c cs Ω+Ω，式中Ωc 是模拟滤波器的3dB 带宽，利用双线性变换，设计一个具有0.2π的3dB 带宽的单极点低通数字滤波器解：由预畸可知c Ω=)2.021tan(2π⨯T =T 65.0∴ H a (s) =Ts T 65.065.0+由双线性变换法可得H(z) =11112|)(--+-⋅=z z T s a s H =Tz z T T65.011265.011++-⋅--=1135.165.2)1(65.0---+z z 5-5 要求通过模拟滤波器设计数字滤波器，给定指标：3dB 截至角频率ωc =π/2，通带内ωp =0.4π处起伏不超过1dB ，阻带内ωs =0.8π处衰减不小于20dB ，用Butterworth 滤波特性实现 （1）用冲击响应不变法 （2）用双线性变换法解：（1）用冲击响应不变法① 先将数字指标转换为低通原型模拟滤波器指标p Ω=Tpω=T π4.0s Ω=Tsω=T π8.0②设计模拟滤波器，求出H a (s) Butterworth 的频响函数为2|)(|Ωj H a =n c2)(11ΩΩ+∴ )(p a j H Ω=ncp 2)(11ΩΩ+=n cp 2)(11ωω+=10110-)(s a j H Ω=n cs 2)(11ΩΩ+=nc s 2)(11ωω+=102010-∴ n =)lg(2)110110lg(1012ps ωω--=2.14 ∴ 取 n = 3 ③ 求c Ω2|)(|Ωj H a =ncs 2)(11ωω+=210-∴ ωc = 62110-sωrad/s = 6998.0π= 0.372π∴ c Ω=Tcω 设T = 1, 则 c Ω= 0.372π④ 求H a (s)查表可得)1)(1(1)(2+'+'+'='s s s s H a∴ H a (s) = )1)(1(1|)(22+Ω+Ω+Ω='Ω='cc c s s a s s s s H c⑤ 由冲击响应不变法 先将H a (s)分解成部分分式H a (s) =11s s A ++22s s A ++33s s A +=则H(z) =1111---z e A T s +1221---z e A T s +1331---z e A T s=（2）用双线性变换法①由预畸求模拟滤波器原型指标p Ω=2tan 2p T ω=T 453.1s Ω=2tan 2s T ω=T 155.0②设计模拟滤波器，求出H a (s) Butterworth 的频响函数为2|)(|Ωj H a =n c2)(11ΩΩ+∴ )(p a j H Ω=ncp 2)(11ΩΩ+=10110-)(s a j H Ω=ncs 2)(11ΩΩ+=102010-∴ n =)lg(2)110110lg(1012ps ΩΩ--=1.51 取n =2③求c Ω2|)(|s a j H Ω=nc2)(11ΩΩ+=210- 取T =1∴ c Ω=62110-Ωsrad/s = 699155.6= 2.862④求H a (s) 查表可得： )(s H a '=14142.112+'+'s sH a (s) = cs s a s H Ω=''|)(=14142.1122+Ω+Ωc cs s=⑤由双线性变换法求 H(z) =11112|)(--+-⋅=z z T s a s H =5-6 已知图5-41h 1(n)是偶对称序列N=8，h 2(n)是h 1(n)圆周位移后的序列。

5.5 离散信号()f n 的波形如习题图5-3所示，试画出下列信号的波形。

(2)(1)(4)(2)(6)(1)(1)(8)(1)()(10)(1)(1)f n f n f n f n f n U n f n U n - +×- -- ---+习题图5-3(2)(1)f n -(4)(2)f n32211()10(2)102100n n n f n n f n n n =-ìï =- 3 =-ìïïï= = Þ = =ííïï = îïï î其他其他+×-(6)(1)(1)f n f n--(8)(1)()f n U n---+f n U n(10)(1)(1)5.17 求下列差分方程所描述的系统的单位样值响应。

1(1)()(2)()9y n y n f n --=解：单位样值响应是指当激励信号为()n d 时系统的零状态响应。

要求单位样值响应，输入()()f n n d =，代入差分方程得：1()(2)()(1)9h n h n n d --= LLL在0n >时，()0n d =，有1()(2)09h n h n --= 特征方程为：2121110,933l l l -= Þ =- =1211()()((2)33n nh n C C \ =-+ LLL0()0(())n h n h n < = Q 时，；因为单位样值响应是零状态响应1()(2)()91(0)(2)(0)191(1)(1)(1)09h n h n n h h h h d d d =-+ \ = -+== -+=由(1)式得： 121122(0)(1)1(0)12111(1)(0332h h h C C C h C C C ì =+==üïïïÞ ýí = -+=ïï=þïî将、代入（2）式得：1111()[((]()2323n nh n U n \ =-+5.18 求习题图5-5所示系统的单位样值响应。