多组分精馏计算

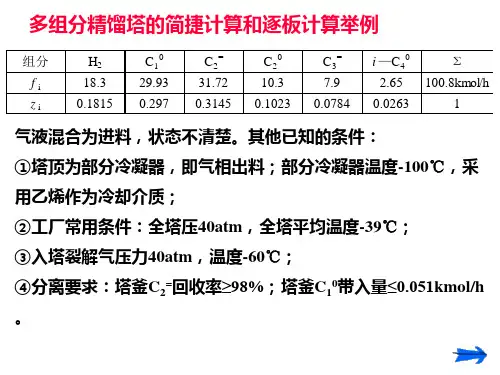
function ConDistillclear allclcglobal F z1 z2 z3 R alpha1 alpha2 alpha3 M1 MN M Nt Nf V1 V D L L1 W F = 40; % 进料流量, kmol/hrR = 5; % 回流比z1 = 0.6; % 苯的进料组成（摩尔分率）z2 = 0.25; % 甲苯的进料组成（摩尔分率）z3 = 1-z1-z2; % 苯乙烯的进料组成（摩尔分率）M1 = 75; % 塔顶冷凝器中的滞液量(kmol)M = 10; % 塔板上的滞液量(kmol)MN = 150; % 塔釜中的滞液量(kmol)q = 1; % 饱和进料tf = 35;dt = 1;% 相对挥发度alpha1 = 2.75;alpha2 = 1;alpha3 = 0.4;Nt = 10; % 塔板总数Nf = 5; % 进料位置V1 = 150; % 从塔釜蒸发上来的蒸汽流量(kmol/hr)% 精馏段V = V1-(1-q)*F;D = V/(R+1); L = V-D;% 提馏段L1 = L+F;W = L1-V1;% 初始化x1和x2---开车时塔内所有板上的x1和x2分别与进料的z1和z2相同x1 = z1 * ones(1,Nt);x2 = z2 * ones(1,Nt);[t,y] = ode45(@DistMassBalances,[0:dt:tf],[x1 x2])% 输出结果x1 = y(:,1:Nt); % 苯的液相组成（摩尔分率）x2 = y(:,Nt+1:2*Nt); % 甲苯的液相组成（摩尔分率）x3 = 1-x1-x2; % 苯乙烯的液相组成（摩尔分率）plot(t,x1(:,1),'r-',t,x2(:,1),'k--',t,x3(:,1),'b:',t,x1(:,end),'r.-',t,x2(:,end),'k-.',t,x3(:,en d),'b.--')xlabel('Time (h)')ylabel('x_1_1, x_1_2, x_1_3, x_N_1, x_N_2, x_N_3')title('塔顶和塔釜产品从进料开始直至稳态的动态浓度曲线')legend('x_1_1','x_1_2','x_1_3','x_N_1','x_N_2','x_N_3')% 稳态图figureplate = 1:Nt;plot(plate,x1(end,:),'r.-',plate,x2(end,:),'k.--',plate,x3(end,:),'b.:')xlabel('塔板')ylabel('稳态时苯,甲苯,苯乙烯的组成')title('稳态时精馏塔的浓度曲线')legend('苯','甲苯','苯乙烯')% ------------------------------------------------------------------function dydt = DistMassBalances(t,y) % 物料平衡方程组global F z1 z2 z3 R alpha1 alpha2 alpha3 M1 MN M Nt Nf V1 V D L L1 W x1 = y(1:Nt); % 组分1（苯）x2 = y(Nt+1:2*Nt); % 组分2（甲苯）x3 = 1-x1-x2; % 组分3（苯乙烯）% 气相平衡denom = alpha1*x1+alpha2*x2+alpha3*x3;y1 = alpha1*x1./denom;y2 = alpha2*x2./denom;% 对塔顶冷凝器（i = 1）i = 1;dx1dt(i) = (V*y1(i+1)-(L+D)*x1(i))/M1;dx2dt(i) = (V*y2(i+1)-(L+D)*x2(i))/M1;% 精馏段（i = 2~Nf-1）for i=2:Nf-1dx1dt(i) = (L*(x1(i-1)-x1(i))+V*(y1(i+1)-y1(i)))/M;dx2dt(i) = (L*(x2(i-1)-x2(i))+V*(y2(i+1)-y2(i)))/M;end% 进料板（i = Nf）i = Nf;dx1dt(i) = (F*z1+L*x1(i-1)-L1*x1(i)+V1*y1(i+1)-V*y1(i))/M;dx2dt(i) = (F*z2+L*x2(i-1)-L1*x2(i)+V1*y2(i+1)-V*y2(i))/M;% 提馏段（Nf+1~Nt-1）for i=Nf+1:Nt-1dx1dt(i) = (L1*(x1(i-1)-x1(i))+V1*(y1(i+1)-y1(i)))/M;dx2dt(i) = (L1*(x2(i-1)-x2(i))+V1*(y2(i+1)-y2(i)))/M;end % 塔釜（i = Nt）i = Nt;dx1dt(i) = (L1*x1(i-1)-V1*y1(i)-W*x1(i))/MN;dx2dt(i) = (L1*x2(i-1)-V1*y2(i)-W*x2(i))/MN;function BatchDistill% 假设：% 1. 沸腾上升的蒸汽流量（V）恒定；% 2. 下降的液体摩尔流量（L）恒定；% 3. 塔板上的滞液量（M）恒定；% 4. 再沸器和塔顶冷凝器中的滞液量恒定。

第三章 多组分精馏在化工原理课程中，对双组分精馏和单组分吸收等简单传质过程进行过较详尽的讨论。

然而，在化工生产实际中，遇到更多的是含有较多组分或复杂物系的分离与提纯问题。

在设计多组分多级分离问题时，必须用联立或迭代法严格地解数目较多的方程，这就是说必须规定足够多的设计变量，使得未知变量的数目正好等于独立方程数，因此在各种设计的分离过程中，首先就涉及过程条件或独立变量的规定问题。

多组分多级分离问题，由于组分数增多而增加了过程的复杂性。

解这类问题，严格的该用精确的计算机算法，但简捷计算常用于过程设计的初始阶段，是对操作进行粗略分析的常用算法。

§3-1分离系统的变量分析设计分离装置就是要求确定各个物理量的数值，但设计的第一步还不是选择变量的具体数值，而是要知道在设计时所需要指定的独立变量的数目，即设计变量。

一、设计变量1.设计变量⎩⎨⎧-=：可调设计变量固定设计变量a x c v i N N N N N :v N ：描述系统所需的独立变量总数。

c N ：各独立变量之间可以列出的方程式数和给定的条件，为约束关系数。

要确定i N ，需正确确定v N 和c N ，一般采用郭慕孙发表在AIchE J （美国化学工程师学会），1956（2）：240-248的方法，该法的特点是简单、方便，不易出错，因而一直沿用至今。

郭氏法的基本原则是将一个装置分解为若干进行简单过程的单元，由每一单元的独立变量数e v N 和约束数e c N 求出每一单元的设计变量数e i N ，然后再由单元的设计变量数计算出装置的设计变量数E i N 。

在设计变量i N 中，又被分为固定设计变量x N 和可调设计变量a N ，x N 是指确定进料物流的那些变量（进料组成和流量）以及系统的压力，这些变量常常是由单元在整个装置中的地位，或装置在整个流程中的地位所决定，也就是说，实际上不要由设计者来指定，而a N 才是真正要由设计者来确定的，因此郭氏法的目的是确定正确的a N 值。

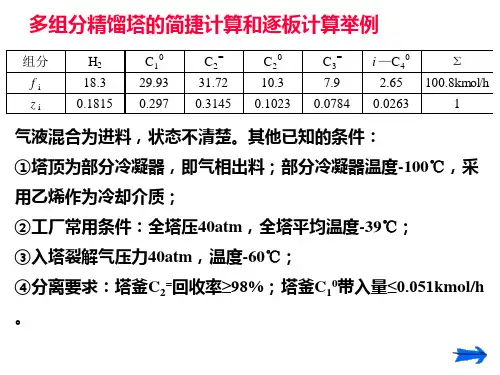
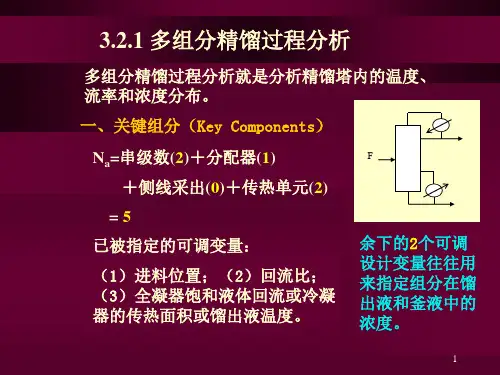
多元连续精馏的计算简介一、全塔物料衡算在多元精馏塔中，通常吧对分离程度起决定作用而必须这种控制的组分称为关键组分，其中挥发度较大的称为轻关键组分，挥发度较小的称为重关键组分。

图9—40挥发度(a)中若规定塔1的分离目标是A 、B ，则A 是轻关键组分，B 是重关键组分；而在图9—40（b ）中，若规定塔1的分离目标是B 、C ，则B 是轻关键组分，C 是重关键组分。

对二元连续精馏过程，全塔物料应该满足式（9—24）和（9－25）。

若已知原料液量F 、组成F x 以及分离要求D W x x 、，则馏出液量D 和釜液量W 就能计算出来。

而对多元连续精馏过程而言，在馏出液和釜液重仍只能规定一个组分的浓度（通常式关键组分的浓度），因为在该设计条件下就可确定精馏塔的理论板数，从而随之确定其余组分的浓度。

换句话说，另外组分的浓度不能任意规定，它们受到精馏塔分离能力的制约。

由于上述原因，多元连续精馏塔重单凭全塔物料衡算还不能确定塔顶、底的量和组成。

以精馏A 、B 、C 三元物系的精馏塔为例，全塔物料衡算关系为AF AD AW BFBD BW F D WFx D x W x Fx D x W x=+⎧⎪=+⎨⎪=+⎩ （9—87） 若已知原料液量F 和组成AF BF x x 、，以及选定的关键组分A 、B 在塔底和塔顶的浓度要求AW BD x x 、，则剩余的四个未知数——馏出液量D 、釜液量W 、组成AD x 和B W x 不能根据式（9—87）直接计算，尚缺一个方程。

为此通常采用一些假定给予补足。

若组分数增多，则需要补足的方程数也增多，因为每增加一个组分，方程数增加一个，而未知数却要增加两个。

总体来说，对C 各组分的多元精馏，全塔物料衡算需要补足的方程数为C —2个。

根据补足方程的不同形式，全塔物料衡算可分为清洗分割和非清晰分割两种。

1、1、 清晰分割若选取的轻、重关键组分式相邻组分，且这两个关键组分间的相对挥发度较大，其分离要求也较高，即轻、重关键组分分别在塔底、塔顶产品中的浓度较低。