扭簧设计公式及图例
- 格式:doc
- 大小:80.00 KB
- 文档页数:3

扭簧设计1. 简介扭簧是一种常见的机械弹性元件,广泛应用于各种机械装置中。
它具有弹性变形能力,能够承受旋转或回转运动时的扭矩,常用于提供力矩或恢复力的作用。
本文将介绍扭簧的设计原理、计算方法和注意事项。
2. 设计原理扭簧的设计需要考虑以下几个关键因素:2.1 材料选择扭簧通常使用优质的弹簧钢材料,如65MN、60SI2MN等。
这些材料具有良好的弹性和硬度,能够确保扭簧的稳定性和耐久性。
2.2 弹性系数扭簧的弹性系数是一项重要的设计参数,用于描述扭簧的刚度。
弹性系数决定了扭簧所能承受的最大扭力和变形程度。
在设计过程中,需要合理选择弹性系数,使得扭簧在工作条件下能够满足所需的扭矩和回弹力。
2.3 螺旋方向扭簧的螺旋方向分为左旋和右旋,具体选择取决于应用需求。
在实际应用中,需要根据装置的运动方式和力矩要求来确定扭簧的螺旋方向,以确保扭簧可以提供所需的扭矩和回弹力。
3. 计算方法扭簧的设计计算需要考虑以下几个方面:3.1 扭矩计算根据应用需求和工作条件,可以通过扭矩计算公式来确定扭簧的设计参数。
一般情况下,扭矩计算公式为:T = K * φ * G式中,T表示扭矩,K表示弹簧的弹性系数,φ表示扭簧的角度变形,G表示扭簧的几何形状参数。
3.2 变形计算扭簧的变形计算需要考虑弹簧材料的弹性模量和几何参数。
一般情况下,变形计算公式为:φ = (T * L) / (G * d^4)式中,φ表示扭簧的角度变形,T表示扭矩,L表示扭簧的长度,G表示扭簧的剪切模量,d表示扭簧的直径。
3.3 弹性系数计算扭簧的弹性系数计算需要考虑弹簧材料的切变模量和几何参数。
一般情况下,弹性系数计算公式为:K = (G * d^4) / (8 * D^3 * n)式中,K表示弹性系数,G表示扭簧的剪切模量,d表示扭簧的直径,D表示扭簧的平均直径,n表示扭簧的总匝数。
4. 注意事项在扭簧设计过程中,需要注意以下几点:•根据应用需求选择合适的弹簧钢材料,确保扭簧的强度和耐久性;•合理选择扭簧的弹性系数,以满足所需的扭矩和回弹力;•在设计过程中考虑扭簧的螺旋方向,以适应装置的运动方式和力矩要求;•使用合适的计算方法,准确计算扭簧的扭矩、变形和弹性系数;•定期检查和维护扭簧,确保其正常工作。

压簧、拉簧、扭簧弹力计算公式压力弹簧压力弹簧的设计数据,除弹簧尺寸外,更需要计算出最大负荷及变位尺寸的负荷;·弹簧常数:以k表示,当弹簧被压缩时,每增加1mm距离的负荷(kgf/mm);·弹簧常数公式(单位:kgf/mm):G=线材的钢性模数:琴钢丝G=8000,不锈钢丝G=7300,磷青铜线G=4500 ,黄铜线G=3500d=线径Do=OD=外径Di=ID=内径Dm=MD=中径=Do-dN=总圈数Nc=有效圈数=N-2弹簧常数计算范例:线径=2.0mm , 外径=22mm , 总圈数=5.5圈 ,钢丝材质=琴钢丝拉力弹簧的 k值与压力弹簧的计算公式相同·拉力弹簧的初张力:初张力等于适足拉开互相紧贴的弹簧并圈所需的力,初张力在弹簧卷制成形后发生。
拉力弹簧在制作时,因钢丝材质、线径、弹簧指数、静电、润滑油脂、热处理、电镀等不同,使得每个拉力弹簧初始拉力产生不平均的现象。
所以安装各规格的拉力弹簧时,应预拉至各并圈之间稍为分开一些间距所需的力称为初张力。
·初张力=P-(k×F1)=最大负荷-(弹簧常数×拉伸长度)·弹簧常数:以 k 表示,当弹簧被扭转时,每增加1°扭转角的负荷 (kgf/mm).·弹簧常数公式(单位:kgf/mm):E=线材之钢性模数:琴钢丝E=21000 ,不锈钢丝E=19400 ,磷青铜线E=11200 ,黄铜线E=11200d=线径Do=OD=外径Di=ID=内径Dm=MD=中径=Do-dN=总圈数R=负荷作用的力臂p=3.1416。

扭簧扭矩计算公式(实用版)目录1.扭簧扭矩计算公式的概念与应用背景2.扭簧扭矩计算公式的推导与解释3.扭簧扭矩计算公式在实际应用中的例子4.扭簧扭矩计算公式的局限性与改进方向正文扭簧扭矩计算公式是一种计算物体在扭转过程中产生的扭矩的数学公式。
扭簧是一种常见的弹性元件,广泛应用于各种扭转控制系统中,例如,汽车底盘系统、发动机曲轴、电机等。
在这些应用中,计算扭簧扭矩对于分析系统的力学性能和设计控制策略具有重要意义。
一、扭簧扭矩计算公式的概念与应用背景扭簧扭矩计算公式是基于弹性力学原理推导得到的。
扭簧在受到外力作用时,会产生扭转变形,这种变形会导致一个力矩,即扭矩。
根据胡克定律,弹性元件的应变与施加的力成正比,可以得到扭簧扭矩计算公式。
二、扭簧扭矩计算公式的推导与解释扭簧扭矩计算公式为:T = G * (α * l)其中,T 表示扭矩,G 表示扭簧的弹性模量,α表示扭簧的扭转角度,l 表示扭簧的长度。
这个公式的推导过程如下:假设有一个长为 l 的扭簧,在扭转过程中产生了一个角度α。
根据胡克定律,扭簧所受的力 F 与施加的力矩 M 的关系为:F =G * αM = F * l将 F 代入 M 的公式中,得到:M = G * α * l由于扭矩 T 等于力矩 M,所以:T = G * α * l这就是扭簧扭矩计算公式。
三、扭簧扭矩计算公式在实际应用中的例子假设有一个电机,它的额定功率为 P,额定转速为 n。
根据电机的额定功率和额定转速,可以求出电机的额定扭矩 T:T = P / (2 * π * n / 60)将 P、n 代入公式,得到:T = P * 60 / (2 * π * n)这个公式实际上就是扭簧扭矩计算公式在电机领域的具体应用。
四、扭簧扭矩计算公式的局限性与改进方向扭簧扭矩计算公式虽然可以用于计算物体在扭转过程中产生的扭矩,但它也有一些局限性。
例如,它只能计算线性扭转,不能计算非线性扭转;它只能计算静载荷下的扭矩,不能计算动载荷下的扭矩等。

扭簧扭力计算引言:扭簧是一种常见的机械元件,广泛应用于各种机械装置中。
扭簧的扭力是指扭簧在受到扭转时所产生的力矩,它是扭簧设计和应用的重要参数。
本文将介绍扭簧扭力计算的基本原理和方法。
一、扭簧的基本结构和工作原理扭簧是一种弹性元件,一般由圆形或方形截面的金属线材经过弯曲成螺旋形而制成。
扭簧的两端固定在机械装置中,当受到扭转力矩时,扭簧会产生弹性变形,存储弹性能量,并产生相应的力矩。
二、扭簧扭力计算的基本原理扭簧的扭力计算涉及到扭簧的几何参数、材料特性和工作条件等因素。
基本原理是根据胡克定律,即扭簧的扭转角度与所受扭矩成正比,而与扭簧的长度和材料刚度等因素有关。
根据扭簧的力学模型和胡克定律,可以得到扭簧的扭力计算公式。
三、扭簧扭力计算的方法1. 确定扭簧的几何参数,包括扭簧的外径、内径、螺距、螺旋角等。
2. 确定扭簧的材料特性,包括弹性模量、剪切模量、杨氏模量等。
3. 根据扭簧的工作条件,确定扭簧所受的扭转角度。
4. 根据扭簧的力学模型和胡克定律,计算扭簧的扭力。
四、扭簧扭力计算的注意事项1. 在计算扭力时,应考虑扭簧的非线性特性,即当扭转角度较大时,扭簧的刚度会发生变化。
2. 在实际应用中,扭簧通常会受到额外的负载,如受力物体的重量或其他外力的作用,这些负载应当考虑在扭力计算中。
3. 扭簧的实际工作寿命与其所受的循环次数密切相关,因此在扭簧设计时,应根据实际工况和使用寿命要求,合理选择扭簧的材料和几何尺寸。
五、扭簧扭力计算的应用领域扭簧扭力计算广泛应用于各种机械装置的设计和优化中。
例如,汽车悬挂系统中的扭簧、家用电器中的弹簧开关、工业机械中的传动系统等都需要进行扭力计算。
六、结论扭簧扭力计算是扭簧设计和应用中的重要环节,通过合理计算扭力可以保证扭簧在工作中的安全性和可靠性。
在实际应用中,还应考虑到扭簧的非线性特性、附加负载和工作寿命等因素,以获得更准确和可靠的扭簧设计参数。
总结:本文介绍了扭簧扭力计算的基本原理和方法,强调了在计算中应注意的事项和实际应用中的一些问题。


扭簧设计计算范文扭簧是一种常见的弹性元件,适用于许多机械设备和装置,用于提供扭矩和旋转力。
在设计扭簧时,我们需要考虑几个关键因素,包括应力、变形、传动比、扭转角度和扭转刚度等方面。
下面将详细介绍扭簧的设计计算。
1.确定扭簧的使用要求:在设计扭簧之前,首先需要明确扭簧的使用要求,包括扭矩、转速、工作时间等。
这些参数将直接影响到扭簧的设计和选择。
2.计算扭簧所受的最大应力:根据扭簧所需的扭矩和材料的弹性模量,可以计算出扭簧所受的最大应力。
常用的计算公式为:τ=(K・T)/(π・D^3)其中,τ为扭簧的最大剪应力,K为扭簧常数,T为扭矩,D为扭簧的直径。
3.计算扭簧的变形量:扭簧在受到外力作用时会发生变形,需要计算出其变形量。
一般来说,扭簧的变形量与其长度、材料的弹性模量和断面系数有关。
计算变形量的常用公式为:δ=(K・T)/(π・D^4/32・G・L)其中,δ为扭簧的变形量,K为扭簧常数,T为扭矩,D为扭簧的直径,G为材料的剪切模量,L为扭簧的长度。
4.根据传动比计算扭簧的目标扭转角度:传动比是扭簧应用中的关键参数,用于确定扭簧所需的扭转角度。
传动比定义为输出转矩与输入转矩之间的比值。
根据传动比,可以计算出扭簧所需的目标扭转角度:φ=φ1+φ2其中,φ为目标扭转角度,φ1为输入转矩所对应的扭转角度,φ2为输出转矩所对应的扭转角度。
5.计算扭簧的扭转刚度:扭簧的扭转刚度反映了其对扭转作用力的抵抗能力。
扭簧的扭转刚度与其几何形状和材料的选择有关。
计算扭簧的扭转刚度常用公式为:k=(G・D^4)/(8・N・R^3)其中,k为扭簧的扭转刚度,G为材料的剪切模量,D为扭簧的直径,N为扭簧的总圈数,R为扭簧的平均半径。
6.校核扭簧的设计参数:根据设计计算的结果,需要对扭簧的设计参数进行校核,确保其满足使用要求和安全性。
校核的内容包括应力、变形、扭转角度和扭转刚度等方面。
在扭簧设计的过程中,除了上述的几个基本计算,还需要考虑其他因素,如扭簧的材料选择、加工工艺、疲劳寿命等。

扭簧弹簧计算器以弹簧设计来图弹簧加工制造为主圆柱螺旋扭转弹簧图纸画法怎么去设计计算一个合理的弹簧目前,广泛应用的弹簧应力和变形的计算公式是根据材料力学推导出来的。
若无一定的实际经验,很难设计和制造出高精度的弹簧,随着设计应力的提高,以往的很多经验不再适用。
例如,弹簧的设计应力提高后,螺旋角加大,会使弹簧的疲劳源由簧圈的内侧转移到外侧。
所有的计算也只是给我们一个大的方向从而减少研发成本。
左图是扭转弹簧刚度系数和力度的计算方法。
螺旋线圈构成的圆柱形弹簧,工作线圈间为恒定间距,能够承受垂直于环绕轴沿着卷绕方向和反方向的扭力。
线径大于16mm的弹簧通常为冷卷。
热成型弹簧用于强负载的直径大于10mm的较大尺寸弹簧。
备注:该计算设计用于线圈卷绕方向的扭转负载,不计入弹簧内部或外部导向零件的支撑效果。
也不计入出现的摩擦效果。
线圈之间的可能的摩擦也不计入在内。
扭簧的常见形式··外臂扭转弹簧···内臂扭转弹簧···中心臂扭转弹簧···平列双扭弹簧·弹簧力度设计扭簧按两种基本设计制造:紧和松(线圈间隙)。
如果是静态负载,紧凑的线圈为推荐选项。
但是,工作线圈之间出现摩擦,这将导致弹簧寿命减少。
另外,线圈的过于接近的间隙阻止弹簧完美喷丸。
由于弹簧端部的节构形状,弹簧与导杆的摩擦等均影响弹簧的特性,所以无特殊需要时,不规定特性要求。
如规定弹簧的特性要求时,应采用簧圈间有间隙的弹簧,用指定扭转变形角时的扭力进行考核。
扭转弹簧的类型如上图,前三类为普通形式扭转弹簧,第4种为平列式双扭转弹簧。
平列双扭转弹簧,是用一根弹簧材料在同一芯轴上,向相反方向缠绕所得的两个圈数相同的弹簧。
其中每一个弹簧的扭转度,相当于以此两个弹簧的总长作为一单个弹簧使用时的2倍。
平列双扭弹簧的刚度为其单个弹簧的4倍,变形量则为单个弹簧的1/4.因此,这种平列双扭转弹簧效率高。

扭簧扭矩计算公式摘要:I.扭簧扭矩计算公式简介A.扭簧的定义和作用B.扭簧扭矩计算公式的基本原理II.扭簧扭矩计算公式推导A.扭簧的物理模型B.扭矩的计算公式C.扭簧扭矩计算公式的推导过程III.扭簧扭矩计算公式应用A.实际工程中的扭簧扭矩计算B.扭簧扭矩计算公式在机械设计中的应用C.扭簧扭矩计算公式在汽车工程中的应用IV.扭簧扭矩计算公式局限性及未来发展A.扭簧扭矩计算公式的局限性B.扭簧扭矩计算公式的发展趋势正文:I.扭簧扭矩计算公式简介扭簧,又称为扭矩弹簧,是一种可以存储和释放能量的弹性元件。
它广泛应用于各种机械设备和汽车等交通工具中,用于减震、储能和传动等。
扭簧扭矩计算公式是计算扭簧在一定条件下所产生扭矩的公式,它对于设计和分析扭簧的性能具有重要意义。
II.扭簧扭矩计算公式推导A.扭簧的物理模型扭簧通常由一个长杆和一个绕着长杆转动的圆盘组成。
圆盘固定在一端,而长杆的另一端则连接到一个负载上。
当负载施加力矩时,扭簧发生扭转,存储能量;当负载需要释放能量时,扭簧释放能量,产生扭矩。
B.扭矩的计算公式扭矩是用来描述物体转动的力矩,通常用符号M 表示。
扭矩的计算公式为:M = F × d其中,F 是作用在物体上的力,d 是力作用点到转轴的距离。
C.扭簧扭矩计算公式的推导过程扭簧扭矩计算公式可以根据扭簧的物理模型和扭矩的计算公式推导得出。
首先,我们需要计算出扭簧在发生扭转时所产生的力矩。
根据力矩的计算公式:M = R × T其中,R 是扭簧的半径,T 是扭簧所受的扭矩。
然后,将力矩代入扭矩的计算公式中,得到扭簧扭矩计算公式:T = M / RIII.扭簧扭矩计算公式应用A.实际工程中的扭簧扭矩计算在实际工程中,扭簧扭矩计算公式可以帮助工程师设计和分析扭簧的性能。
例如,在汽车工程中,扭簧扭矩计算公式可以用于计算汽车扭力梁的扭矩,从而优化汽车行驶过程中的稳定性和舒适性。
B.扭簧扭矩计算公式在机械设计中的应用扭簧扭矩计算公式在机械设计中也有广泛的应用。
1. 弹簧刚度:
2. 力值: 其中:G 为材料剪切模量,一般不锈钢取71500Mpa,碳钢取
78500Mpa ;
d 为材料直径;
D 为弹簧中径;
n 为弹簧有效圈数;
f 为变形量(拉压行程)。
3. 应力: K 为曲度系数,公式为: 其中C 为弹簧旋绕比,是弹簧中径与线径的比值,即
4. 下表是GB/T23935-2009(圆柱螺旋弹簧设计计算)中压缩弹簧及拉伸弹簧的试验切应力及许用应力表
表2-1
n D d G 34
,
8P =f 8f 34,
⋅==n D Gd P P K PC K ⋅=⋅=2
3d 8d 8PD ππτC
C C K 615.04414+--=d D
C =
比压簧多了初拉力,加上初拉力就行。
初拉力: 其中初拉力τ0按初切应力图选取,见下图。
三.扭簧:
1.计算刚度 Dn
Ed M 3670'4= Nmm/° 2.扭矩 ϕ⋅=Dn
Ed M 36704
Nmm 式中:d---材料直径;
E---材料的弹性模量,一般不锈钢丝取188000Mpa ,碳素钢丝
取206000Mpa ;
D---弹簧外径;
ϕ---弹簧的扭转行程(角度);
4. 应力: K1为曲度系数,顺旋向扭转取1,逆旋向扭转时按下式:
308τπ⋅=D d P 132
.10K d
M ⋅=σ
下表是GB/T23935-2009(圆柱螺旋弹簧设计计算)中扭转弹簧的试验切应力及许用应力表
C
C C C K 4414221---=。

各种规格双簧设计双扭簧设计公式可通过:扭转弹簧计算器进行自动计算。
此计算器是单扭簧计算器,计算结果X2即为双扭簧的刚度及力度。
双扭簧寿命计算公式,弹簧寿命的计算涉及到一系列的专业数据提取,非专业人员很难计算出合理的结果。
双扭簧设计原理双扭簧利用杠杆原理扭转或转动材料柔软、韧性大的弹性材料,使其具有很大的机械能。
它是一种能承受扭转变形的弹簧,其工作部分也被每个圆紧紧地或分开地包围着。
双扭簧的端部结构加工成各种形状的扭臂,从单扭到双扭,甚至可以根据设计形成各种扭杆的变形。
双扭簧通常用作机械中的平衡机构,并广泛用于工业生产,如汽车、机床和电器。
双扭簧的设计流程拉簧的两端将影响钩的形状和拉簧的自由长度。
该空间可以确定粘合部分的尺寸和外径。
此外,预拉伸载荷决定弹簧的材料和线直径,并且接触部分的尺寸可以调节预拉伸长度。
双扭簧的内径由主轴的尺寸决定,但应考虑双扭簧体扭转后的变化,因此应预留适当的余量。
如果双扭簧装置被嵌入,则必须考虑嵌入空间。
该空间决定弹簧体的外径、自由长度和圈数。
双扭簧工作时,它必须有一个点,可以决定扭杆的长度和形状。
当施力扭杆不起作用时,施力扭杆的长度和形式以及与支点杆的角度可以清楚地定义。
双扭簧设计结构双扭簧是变型弹簧的极点。
单双扭簧到双双扭簧甚至各种扭杆的变形都可以根据设计形成。
用在支撑的心轴或心轴上。
心轴的尺寸允许在列出的偏差中有大约10%的间隙。
如果偏差较大,轴的尺寸将减小。
为了使双扭簧功能处于良好状态,组件中的空间(最小轴向空间)必须足够大。
最小轴向空间不能指线圈的长度。
扭转弹簧应沿线圈缠绕的方向使用。
由于残余应力,最大载荷在松开方向较低。
双扭簧用途双扭簧是由一种弹簧材料在同一芯轴上以相反方向缠绕相同圈数的两种弹簧。
两个弹簧中间是挡圈,两端是增加扭矩的支点。
每个弹簧的扭转刚度相当于两个弹簧中的一个用作单个弹簧时的两倍。
双扭簧的刚度是单弹簧的4倍,变形是单弹簧的1/4。
因此,双扭簧具有高效率。
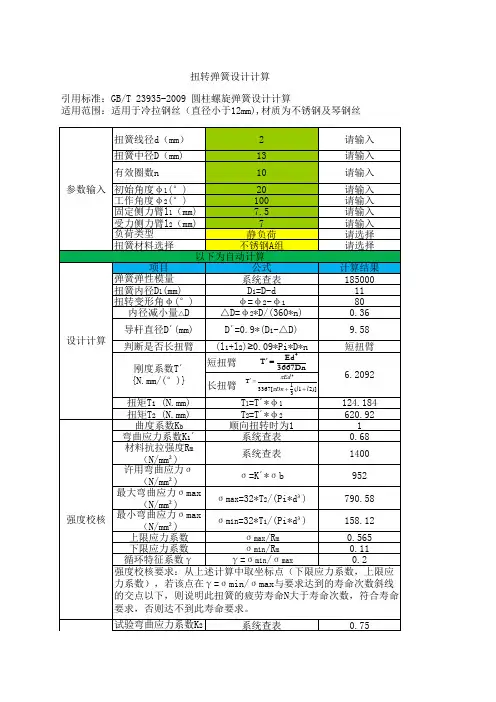
扭转弹簧设计计算扭簧线径d(mm)2请输入扭簧中径D(mm)13请输入有效圈数n 10请输入初始角度φ1(°)20请输入工作角度φ2(°)100请输入固定侧力臂l 1(mm)7.5请输入受力侧力臂l 2(mm)7请输入负荷类型静负荷请选择扭簧材料选择不锈钢A组请选择项目公式计算结果弹簧弹性模量E(MPa)系统查表185000扭簧内径D 1(mm)D 1=D-d 11扭转变形角φ(°)φ=φ2-φ180内径减小量△D △D=φ2*D/(360*n)0.36导杆直径D′(mm)D′=0.9*(D 1-△D)9.58判断是否长扭臂(l 1+l 2)≥0.09*Pi*D*n 短扭臂短扭臂长扭臂扭矩T 1 (N.mm)T 1=T′*φ1124.184扭矩T 2 (N.mm)T 2=T′*φ2620.92曲度系数K b顺向扭转时为11弯曲应力系数K 1′系统查表0.68材料抗拉强度R m (N/mm2)系统查表1400许用弯曲应力σ(N/mm2)σ=K′*σb 952最大弯曲应力σmax (N/mm2)σmax =32*T 2/(Pi*d3)790.58最小弯曲应力σmax (N/mm2)σmin =32*T 1/(Pi*d3)158.12上限应力系数σmax /R m0.565下限应力系数σmin /R m0.11循环特征系数γγ=σmin /σmax0.2试验弯曲应力系数K 2系统查表0.75强度校核校核刚度系数T′{N.mm/(°)} 6.2092强度校核要求:从上述计算中取坐标点(下限应力系数,上限应力系数),若该点在γ=σmin/σmax与要求达到的寿命次数斜线的交点以下,则说明此扭簧的疲劳寿命N大于寿命次数,符合寿命要求,否则达不到此寿命要求。
以下为自动计算参数输入设计计算扭转弹簧设计计算引用标准:GB/T 23935-2009 圆柱螺旋弹簧设计计算适用范围:适用于冷拉钢丝(直径小于12mm),材质为不锈钢及琴钢丝3667Dn Ed ′T 4=)]21(31[3367′T 4l l Dn Ed ++=ππ。