下载文档原格式
流体的连续性方程和动量方程流体力学是研究流体运动和流体力学性质的学科。
在流体力学中，连续性方程和动量方程是两个重要的基本方程。
本文将详细介绍流体的连续性方程和动量方程的定义和应用。
一、流体的连续性方程连续性方程描述了流体的质量守恒原理，表达了流体在空间和时间上的连续性。
连续性方程的数学表达形式为：∂ρ/∂t + ∇·(ρv) = 0其中，ρ是流体的密度，t是时间，v是流体的速度矢量，∇·(ρv)表示速度矢量的散度。
该方程表示，流体的密度在一个闭合曲面上的变化率等于通过该曲面的质量流量。
连续性方程是基于质量守恒原理推导得出的。
它表明，在稳定流动条件下，流体在通道中的截面积变化时，速度会发生相应的变化，以保持质量的守恒。
根据连续性方程，我们可以推导出管道中的速度分布。
在管道的收缩段，速度增加，截面积减小，密度保持不变，从而保证质量守恒。
这也是为什么水管收缩后出水流速增加的原因。
二、流体的动量方程动量方程描述了流体运动的力学性质，表达了流体在空间和时间上的动量守恒。
动量方程的数学表达形式为：ρ(dv/dt) = -∇p + μ∇^2v + F其中，ρ是流体的密度，t是时间，v是流体的速度矢量，p是压强，μ是流体的粘度，∇p表示压强的梯度，∇^2v表示速度的拉普拉斯算子，F是外力的合力。
动量方程由牛顿第二定律推导而来。
它表示，在流体中，流体质点的动量变化等于合外力对质点的作用力。
动量方程用于描述流体在受力作用下的运动状态，通过求解动量方程，可以得到流体的速度分布。
根据动量方程，我们可以推导出流体中的压力分布。
在水管中，如果水流速度增大，则根据动量方程中的负梯度项，压力会降低。
这是因为速度增大会导致动能的增加，压力会减少以保持动量守恒。
综上所述，流体的连续性方程和动量方程是流体力学中的两个基本方程。
连续性方程描述了质量守恒原理，动量方程描述了动量守恒原理。
通过求解这两个方程，我们可以获得流体在空间和时间上的运动状态和力学性质。
第二章 流体运动方程组§1.连续方程§2.作用于流体上的力§3.流体运动方程及其简化形式 §4.能量方程§5.Naver-Stokes 方程的简单解本章重点：流体的三大守恒定律，作用在流体上的力，Naver-Stokes 方程。
作为物体的形态之一，流体也遵循基本的物理规律：质量守恒定律、动量守恒定律和能量守恒定律，其分别对应本章的连续方程、运动方程和能量方程。
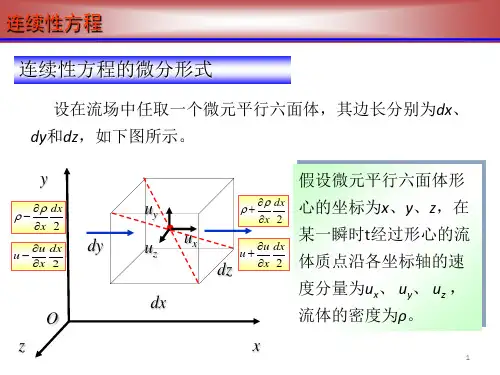
§1.连续方程1. 连续方程 设流体块体积δτδδδ=x y z ，则质量δρδτm =。
由于质量守恒，有：()dd δm =0t （2.1）()d d ρδτ=0t（2.1´）’展开：()d d d d δτρδτρ+=0t t（2.2） 同除δτ，得：()d d d d δτρρδτ+=0t t（2.3）∵()d d δτδτ∇⋅ =1V t（体胀速度）∴（2.3）式可变为:——连续方程（速度散度形式） （2.4）∵d d ρρρ∂⋅∇∂+=V t t，而()ρρ⋅∇∇⋅∇⋅ +ρ V V =V ，则（2.4）式可改写为:——连续方程（质量散度形式） （2.5） 其中称为（速度）散度，表示单位体积的流体通量。
而∇⋅V ()ρ∇⋅V 称为质量散度，表示单位体积的流体质量通量。
质量有净流入,→()ρ∇⋅V <0ρ∂∂>0t（密度增大）；质量有净流出,()ρ∇⋅ V >0→ρ∂∂<0t（密度减小）。
2. 有关流体密度的几种近似 1） 若d d ρ=0t，即const ρ()x,y,z,t =，称为不可压(缩）流体。
∵d d ρ=0t →∇⋅ V =0，∴不可压流体＝（三维）无辐散流体。
2）若d d ρ=0t，且各处的ρ（常数）也一样， const ρ=（不随而异），称为均质（均匀）不可压（缩）流体。
x,y,z,t 3）若ρ∂∂=0t ，则ρ与无关，称为（密度）定常流体（不同于定常流场）。
