一般二阶电路
- 格式:ppt
- 大小:204.50 KB
- 文档页数:8



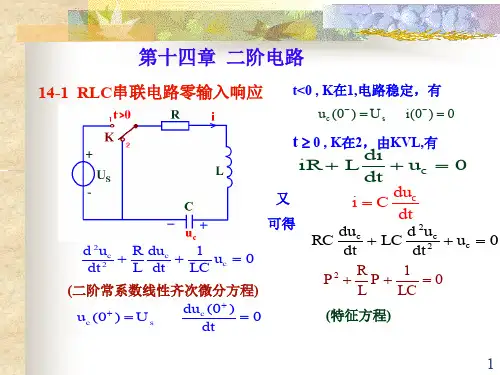



典型rlc二阶电路公式大全
典型的RLC二阶电路包括带有电感L、电阻R和电容C的串联电路和并联电路。
以下是一些常见的RLC二阶电路公式:
1. 自然频率(Resonant Frequency):
ω₀ = 1/√(LC)
2. 响应系数(Damping Factor):
ζ = R/2√(LC)
3. 频率响应函数(Frequency Response Function):
H(jω) = Vout / Vin = 1 / [1 - (ω/ω₀)² + j(2ζω/ω₀)]
4. 响应的幅度(Magnitude of Response):
|H(jω)| = |H(ω)| = 1 / √[1 - (ω/ω₀)²]² + (2ζω/ω₀)²
5. 响应的相位(Phase of Response):
φ = atan{(2ζω/ω₀) / [1 - (ω/ω₀)²]}
6. 峰值频率(Peak Frequency):
f_p = (1/2π) * √[(1 - ζ²) / (LC)]
7. 峰值带宽(Bandwidth):
Δf = (1/2π) * √[(1 - ζ²) / (LC)]
8. 峰值时间(Peak Time):
T_p = 1 / (ζω₀)
以上是一些关于RLC二阶电路的常见公式,可以用于分析和计算不同的电路参数和响应特性。
请注意,其中的符号含义可能会根据具体的文献和教材有所不同,需要根据具体情况进行理解和使用。
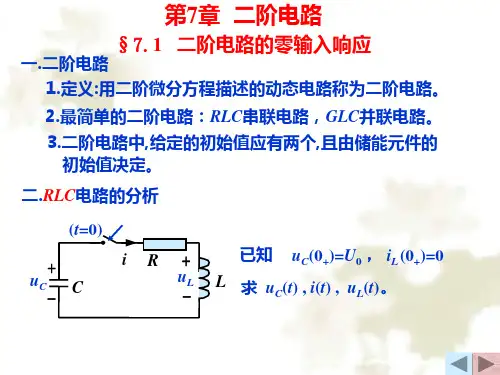


第七章 二阶电路 §7-1 二阶电路的零输入响应用二阶方程描述的动态电路称为二阶电路,当电路有电感,又有电容时就是一个二阶电路,二阶电路中给定的初始条件有2个 一、方程及特征根(RLC 串联)022=++C CC u dt du RC dtu d LC特征根为:LC L R L R p 12221-⎪⎭⎫⎝⎛+-=LC L R L R p 12221-⎪⎭⎫⎝⎛--=零输入响应为:t t P P C e A e A u 2121+= 1.电路的初始条件有三种情况,分别为:①0)0(0)0(≠≠++L C i u ②0)0(0)0(=≠++L C i u ③0)0(0)0(≠=++L C i u我们讨论第二种情况,设0)0()0()0()0(====-+-+L L C C i i u u u2.特征根p 1、p 2有不等负实数根、相等负实数根、一对共轭复数根三种情况,这三种情况决定零输入响应不同。
二、CLR 2>(1P 、2P 有不等负实根)时电路的响应 —是一个非振荡放电过程 1.电容上的电压和电流及电感上的电压响应表达式为:)(2112120t t P P C e P e P P P U u --=LCp p 121=)()()(2121120112210t t t t P P P P C e e P P L U e P e P P P P CU dt du Ci ---=---=-=)(2121120t t P P L e P e P P P U dt di Lu ---==2.响应曲线2112)/ln(P P P P T m -=此时电感电压过0,电流取得最大值m t t 2= 此时电感电压有极值三、CLR 2<(1P 、2P 有共轭复根)时电路的响应—是一个振荡放电过程1.电容上的电压和电流及电感上的电压为: )(2112120t t P P C e P e P P P U u --=[])2)(0)(00t j i t j j e e e e j U ωδβωδβωωω---+-+--=⎥⎦⎤⎢⎣⎡-=+-+-j e e eU t j t t j t2)()(00βωβωδωω)sin(00βωωωδ+=-t e U t)sin(0t e LU i tωωδ-=)sin(00βωωωδ--=-t e U u t其中:2RLδ=0ω=ω= arctg ωβδ= 2.波形图如下:ttπδ3.理想情况下,,2,1,0,00πβωωδ=====LCR 则:)2sin(00πω+=t U u Ct CLUt L U i 00000sin sin ωωω==C L u t U t U u =+=--=)2sin()2sin(0000πωπω 即等幅振荡放电过程。
二阶电路算法摘要:1.二阶电路算法的概述2.二阶电路算法的求解方法3.二阶电路算法的应用案例4.二阶电路算法的优缺点分析正文:一、二阶电路算法的概述二阶电路算法,顾名思义,是一种针对二阶电路的计算方法。
二阶电路是指由两个电感或电容元件、一个电阻元件以及一个电压源或电流源组成的电路。
在电子工程、通信工程等领域,二阶电路具有广泛的应用。
二、二阶电路算法的求解方法求解二阶电路的方法有很多,主要包括以下几种:1.欧姆定律法:适用于电阻型二阶电路,通过欧姆定律可以直接求解电路的电压和电流。
2.电容或电感定律法:适用于电容型或电感型二阶电路,通过电容或电感定律,可以得到电路的电压和电流关系。
3.复数法:也称为相量法,将电路中的电压和电流用复数表示,通过复数的加减运算,可以求解二阶电路。
4.微分方程法:将二阶电路的电压和电流关系建立成微分方程,通过求解微分方程,可以得到电路的解。
三、二阶电路算法的应用案例二阶电路算法在实际应用中有很多案例,例如:1.RLC 电路:由电阻、电感和电容组成的电路,广泛应用于通信系统中的滤波器、振荡器等。
2.LC 振荡器:由电感和电容组成的振荡电路,常用于无线电、广播电视等领域。
3.音频放大器:由电容、电感和晶体管组成的放大电路,用于音频信号的放大。
四、二阶电路算法的优缺点分析二阶电路算法具有一定的优点和缺点:优点:1.适用范围广:可以解决多种类型的二阶电路问题。
2.计算简便:通过简单的加减运算或微分方程求解,计算过程较为简单。
缺点:1.对于复杂电路,求解过程可能较为繁琐。
2.需要掌握一定的电路理论知识,对于初学者可能有一定难度。
总之,二阶电路算法是一种重要的电路计算方法,在实际应用中具有广泛的应用价值。
二阶电路电路元件参数的改变对响应变化趋势的影响在探讨二阶电路电路元件参数的改变对响应变化趋势的影响时,我们首先需要了解什么是二阶电路以及电路元件参数的含义。
二阶电路是指电路中含有二阶导数的电路,通常包括电感和电容等元件。
而电路元件参数则是指这些元件的数值,例如电感的电感值、电容的电容值等。
改变这些参数将会对电路的响应产生什么样的影响呢?让我们一起来深入探讨。
1. 二阶电路的基本概念在介绍二阶电路的基本概念时,我们先来了解一下什么是二阶电路。
二阶电路是指电路中所含有的二阶微分方程,通常包括电感和电容两种元件。
在二阶电路中,电流和电压的变化呈现出二阶导数关系,这种关系决定了电路的响应特性。
2. 电路元件参数的改变对响应的影响接下来,我们将讨论电路元件参数的改变对电路响应的影响。
我们将以电感值和电容值为例,讨论它们对电路响应的影响。
2.1 电感值的改变当电路中的电感值发生改变时,电路的响应也会出现相应的变化。
一般来说,电感值的增大会导致电路的谐振频率降低,从而影响电路的频率响应特性;而电感值的减小则会导致电路的谐振频率升高,影响电路的频率响应特性。
电感值的改变还会影响电路的幅频特性和相频特性,进而改变电路的频率响应曲线。
2.2 电容值的改变与电感值类似,电路中的电容值的改变也会对电路的响应产生影响。
一般来说,电容值的增大会导致电路的谐振频率升高,从而影响电路的频率响应特性;而电容值的减小则会导致电路的谐振频率降低,影响电路的频率响应特性。
电容值的改变还会影响电路的幅频特性和相频特性,进而改变电路的频率响应曲线。
3. 个人观点和理解在二阶电路电路元件参数的改变对响应变化趋势的影响这个主题下,我个人认为电路元件参数的改变能够显著地影响电路的响应特性。
通过改变电感值和电容值等参数,我们可以调节电路的谐振频率、幅频特性和相频特性,从而实现对电路响应的精确控制。
这种精确控制不仅在电路设计和调试中具有重要意义,还可以为电路应用提供更灵活的解决方案。
第七章二阶电路一、教学基本要求1、了解二阶电路零状态响应、零输入响应、全响应的物理意义和概念。
2、会分析简单的二阶电路。
二、教学重点与难点1. 教学重点: (1).二阶电路的方程和特征根(2). 二阶电路的零输入响应、零状态响应、全响应的概念(3). 二阶电路过渡过程的过阻尼、欠阻尼及临界阻尼的概念及分析(4). 二阶电路的阶跃响应。
2.教学难点:1.应用基尔霍夫定律和电感、电容的元件特性建立动态电路方程;2. 二阶电路的过阻尼、欠阻尼及临界阻尼放电过程分析方法和基本物理概念。
三、本章与其它章节的联系:本章讨论的仍是线性电路,因此前面讨论的线性电路的分析方法和定理全部可以用于本章的分析中。
第 9 章讨论的线性电路的正弦稳态响应就是动态电路在正弦激励下的稳态分量的求解。
四、学时安排总学时:2五、教学内容§7.1 二阶电路的零输入响应二阶电路是指用二阶微分方程来描述的电路。
下面主要通过分析RLC 串联电路来说明求二阶电路响应的方法。
1.方程和初始条件图 7.1图7.1所示的RLC串联电路在t=0时刻闭合开关,设电容原本充有电压U0,此电路的放电过程是二阶电路的零输入响应问题。
电路的KVL方程及元件的VCR 为:若以电容电压为变量,从以上方程中消去其他变量得二阶齐次微分方程:初始条件为:u C (0+)= U 0 ,i (0+)=0 ,或若以电感电流为变量,则方程为:初始条件为:i (0+)=0 ,根据得:2.二阶微分方程的解及其物理意义以电容电压为变量,电路方程为:从中得特征方程:特征根为:上式表明特征根仅与电路参数和结构有关,而与激励和初始储能无关。
当R、L、C的参数不同,特征根为不同的形式。
下面分三种情况讨论。
(1)当时,特征根为两个不相等的负实根,电路处于过阻尼状态。
此时方程的解为:由初始条件:,得:即:因此电容电压为:电流为:电感电压为:图7.2给出了电容电压、电流和电感电压随时间变化的波形,从中可以看出,电容电压和电流始终不改变方向,且最终衰减至零,说明电容始终在释放能量,称过阻尼放电。