二阶动态电路分析

二阶非线性动态电路分析题目：二阶非线性电路如图1，R=10Ω,i=ϕ+32.0ϕ，C=0.25×210-F,C U (-0)=2V.求C U (t)（t>0）,并画出t>0时ϕ-C U 的相图。

图1.二阶非线性电路理论分析:解：取ϕ与C U 为状态变量，t>0时： 32.0-ϕϕ-=-==i i dt du C C c => 380-400ϕϕ-=dtdu c 32.0ϕϕϕR R U Ri U u dt d C C L --=-== => 3210ϕϕϕ--=C U dtd Matlab 求解：此非线性动态电路难求解析解，因此利用Matlab 做数值求解，得到响应在离散时刻的近似值，再根据此离散值做出响应相关图像。

Matlab 求解的原理是利用ode45函数解微分方程组。

ode45表示采用四阶，五阶runge-kutta 单步算法。

ode45函数语法为[T,Y] = ode45(odefun, tspan,y0)，这里tspan 选择0到2.5s ，初值C U =2,ϕ=0。

首先写一个函数M 文件列出待求解方程组如下：function dy=rlc(t,y)dy=zeros(2,1)dy(1)=-400*y(2)-80*y(2)^3dy(2)=y(1)-10*y(2)-2*y(2)^3end在命令行输入[t,y]=ode45(@rlc,[0 2.5],[2 0])，可求出响应C U （t ）、ϕ（t ）数值解。

在命令行输入：plot(t,y(:,1))grid on 数值解title('Uc-t曲线')xlabel('t')ylabel('Uc')可得到Uc(t)曲线。

可以更直观的观查Uc随时间的变化。

图2 Uc响应曲线同理可得到ϕ（t）图像如图3所示：图3 ψ-t曲线同理可得到ϕ-Uc相图如图4所示。

图4 ϕ-Uc相图结果分析：观察图形可发现，该电路处于振荡放电过程，未知量L 满足不等式R<C L2。

实验二十一 二阶动态电路设计
一、实验内容
已知RLC 串联电路, 输入为单位阶跃信号, 设计元件参数, 要求电容负载输出电压的超调量约为20%, 调节时间0.003秒。

先进行理论设计和仿真分析, 连接好电路后, 再通过示波器观察实际输入和输出曲线。

二、实验原理图和理论分析
)()()()()(22t t u t u dt t du RC dt
t u d LC S C C C ε==++ 二阶电路的阶跃响应为)sin(1)(0βωωωδ++
=-t e t u t C 超调量为21%ζζπ
σ--==e
M P 调节时间为n s t ζω3=
(5%稳态范围)
,
, C
L n ⋅=21ω L R n ⋅⋅=ωζ2 选用电容C=4.7
F, 由以上推导得L=44.2mH, R=88.4
三、实验设备
函数信号发生器
KTDG-4可调式电感箱0~100mH
可调式电阻箱0~99999.9Ω
交流电压表, 交流电流表
双踪示波器
四、仿真实验
利用EWB 软件, 仿真模型图如下
运行结果如下
电容电阻电感在实验台上连接好电
路, 测量结果如下。

电压有效值
电流有效值
利用示波器观测输入电压和输出电容上电压曲线:
六、数据处理和实验结论
略。

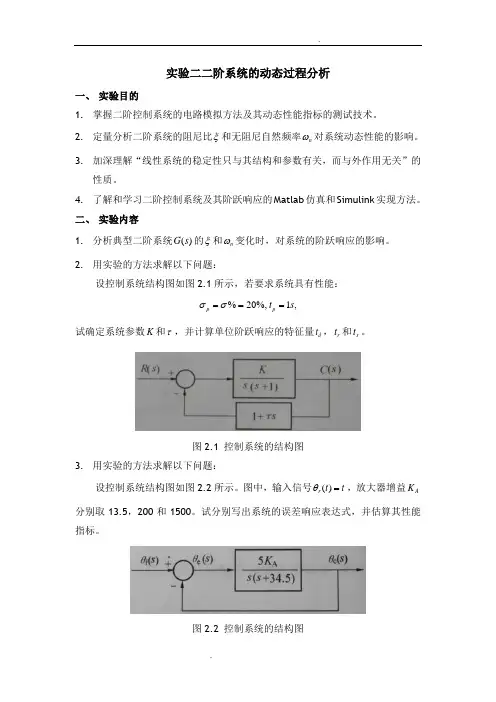
实验二二阶系统的动态过程分析一、 实验目的1. 掌握二阶控制系统的电路模拟方法及其动态性能指标的测试技术。

2. 定量分析二阶系统的阻尼比ξ和无阻尼自然频率n ω对系统动态性能的影响。

3. 加深理解“线性系统的稳定性只与其结构和参数有关，而与外作用无关”的性质。

4. 了解和学习二阶控制系统及其阶跃响应的Matlab 仿真和Simulink 实现方法。

二、 实验内容1. 分析典型二阶系统()G s 的ξ和n ω变化时，对系统的阶跃响应的影响。

2. 用实验的方法求解以下问题：设控制系统结构图如图2.1所示，若要求系统具有性能：%20%,1,p p t s σσ===试确定系统参数K 和τ，并计算单位阶跃响应的特征量d t ，r t 和s t 。

图2.1 控制系统的结构图3. 用实验的方法求解以下问题：设控制系统结构图如图2.2所示。

图中，输入信号()r t t θ=，放大器增益AK 分别取13.5，200和1500。

试分别写出系统的误差响应表达式，并估算其性能指标。

图2.2 控制系统的结构图三、实验原理任何一个给定的线性控制系统，都可以分解为若干个典型环节的组合。

将每个典型环节的模拟电路按系统的方块图连接起来，就得到控制系统的模拟电路图。

通常，二阶控制系统222()2nn nG ssωξωω=++可以分解为一个比例环节、一个惯性环节和一个积分环节，其结构原理如图 2.3所示，对应的模拟电路图如图2.4所示。

图2.3 二阶系统的结构原理图图2.4 二阶系统的模拟电路原理图图2.4中：()(),()()r cu t r t u t c t==-。

比例常数（增益系数）21RKR=，惯性时间常数131T R C=，积分时间常数242T R C=。

其闭环传递函数为：12221112()1()(1)crKU s TTKKU s T s T s K s sT TT==++++(0.1) 又：二阶控制系统的特性由两个参数来描述，即系统的阻尼比ξ和无阻尼自然频率n ω。

一阶二阶动态电路实验报告前言本文介绍了一阶二阶动态电路实验的相关内容，包括实验准备、步骤、实验结果的分析以及结论。

动态电路是一种重要的电路技术，在很多方面都起着重要的作用。

它可以应用于多种电子设备中，如电脑、摄像机和收录机等。

本实验介绍的是测试一阶二阶动态电路的实例，并解释了其中的一些概念和特性，使我们更加理解动态电路技术。

实验准备在本实验中，我们需要准备以下几种实验用品：一阶（二极管，电容，电阻）和二阶（二极管，电容，电阻，特定电路板）的模块，以及一台电脑。

实验步骤1）确定模块原理图：首先，我们需要确定对应的模块原理图，确定每个模块的输入和输出端口。

2）连接电路：然后，组装模块，连接电路，将各个模块连接起来，确保模块与电路之间的联系。

3）测试电路：接着，使用数据采集仪来测量每个模块的输入信号和输出信号，对电路进行测试。

4）对电路进行分析：最后，根据测量的结果，对电路进行分析，分析电路中每个元件的功能，并确定电路的特性。

实验结果在本实验中，我们所做的实验采用的是一阶和二阶的动态电路，我们测量了各个模块的输入和输出信号，最终得出以下结论：（1）一阶动态电路的升降沿响应时间可以在设定范围内调节；（2）二阶动态电路的输入与输出之间存在一定的延迟时间；（3）随着负载变化，动态电路的性能会受到影响；（4）一阶和二阶动态电路的性能是不同的。

结论通过本次实验，我们学会了如何测试一阶和二阶动态电路，以及他们在当今电子产品中的应用。

在模拟信号控制领域，一阶和二阶动态电路都得到了广泛的应用。

使用一阶动态电路可以满足一般要求，而使用二阶动态电路可以满足高精度的要求。

二阶动态电路响应的研究实验报告嘿，大家好！今天咱们聊聊一个让人兴奋的话题——二阶动态电路响应。

听上去是不是有点深奥？别担心，我来给你们揭开这个神秘的面纱。

这就像是一个电路在回应我们的“指令”，就像小狗听到主人的口令一样，乖乖地反应。

不过呢，这种反应可不是简单的坐下、转圈圈，而是复杂得多。

想象一下，我们把电路看成是一位艺术家，二阶动态电路就像是他用来创作的画笔。

这画笔的灵敏度、反应速度，还有画出的每一笔，每一划，都是我们研究的重点。

二阶动态电路有两个能量储存元件——电感和电容，它们就像是电路里的双胞胎，一起工作，互相影响。

你可能会问，这双胞胎到底有多厉害？嘿，这可得看看它们的“化学反应”了。

在我们的实验中，我们设置了一些有趣的场景，让电路在不同条件下进行“表演”。

想象一下，你调高音量，看看电路是怎么回应的。

嘿，瞬间，你就能看到电压和电流的波动，简直像是在看一场电气交响乐！这些变化就像是电路在告诉你，它感受到了什么。

就像人在舞台上跳舞，随着音乐的节奏而舞动。

我们称这些反应为“响应”，就像小猫看到鱼一样，立刻就能“扑”上去。

我们还得提到一个小秘密，那就是“自然频率”。

这是电路的“特色”，就像每个人都有自己独特的声音。

当我们施加一个信号，电路就会在这个频率上表现得特别活跃。

想想看，就像一个歌手在高音区时，整个气氛都被点燃了。

我们通过实验观察到，电路在自然频率附近的反应特别明显，像个兴奋的小孩子，跃跃欲试，恨不得马上就来个大展示。

实验中也不乏一些小插曲。

我们的电路表现得不太“听话”，比如出现了过冲和下冲，就像小孩闹脾气一样。

这个时候，我们就得耐心点，调整电路的参数，试图让它回到正常的“轨道”上。

你要知道，电路就像一个情绪丰富的孩子，有时候需要些耐心和引导，才能让它表现得更好。

咱们得聊聊数据分析。

这部分虽然有点严肃，但其实也挺有趣的。

我们用一些图表来展示电路的响应情况，就像是在看运动会的成绩单。

每一条曲线、每一个数据点，都是电路表演的证据。