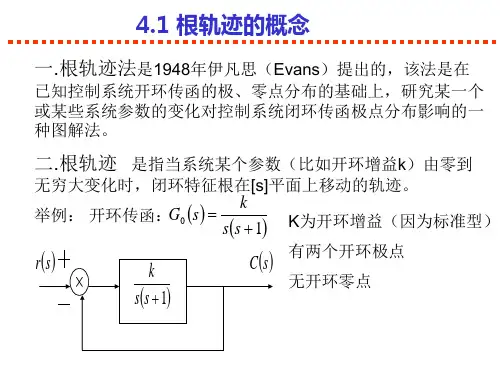
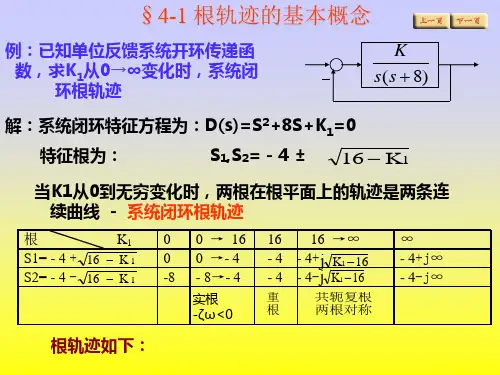
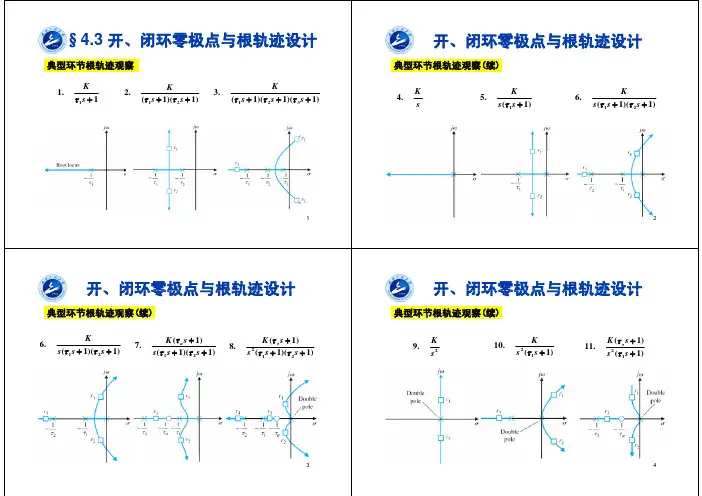
➢根轨迹的渐近线 根轨迹的渐近线就是确定当开环零点数目m小于极点 数目n时,(n-m)条根轨迹沿什么方向趋于[s]平面无 穷远处。由式(4-1-7)及式(4-2-1)求得
k (s z1)(s z2 )(s zm ) 1 (s p1)(s p2 )(s pn )
(4-2-6)
g(t) c(t) 1 et /
闭环系统特征方程为
f (s) s3 3s2 2s k 0
df (s) 3s2 6s 2 0 ds
s1 0.422, s2 1.578
由前边分析得知,s2 不是根轨迹上的点,故舍 去。s1是根轨迹与实轴分离点坐标。最后画出
根轨迹如图4-2-4所示。
图4-2-4 例4-2-1的跟轨迹图
利用多项式乘法和除法,由式(4-2-6)可得
n
s n ( pi )s n1
k
i 1 m
s m ( z j )s m1
j 1
m
n
s nm ( z j
pi )s nm1
j 1
i 1
将式(4-2-8)代入上式可得
m
n
(s )nm snm ( z j pi )snm1
(n m)
(4-2-1)
式中 s z j ( j 1,2,, m) 为系统的开环零点 s pi (i 1,2,, n) 为系统的开环极点
k称为根轨迹增益或根轨迹放大倍数。设系统为v型, 即有s=0的开环极点,将式(4-2-1)改写为
G(s)H (s)
K (1s 1)( 2s 1)( ms 1)
当1<k<∞时,两个闭环极点变为一对共轭复数极点
明当sk1→、s21、∞ 时s12,位js1于、k(s-121,将,且j趋0s1)、向点s于且2 无平的限行实远于部处虚不。轴随图的k变4直-化1线的,上控说。