第四章 根轨迹方程
- 格式:doc
- 大小:715.50 KB
- 文档页数:21

第四章根轨迹法4-1 根轨迹法的基本概念4-2 常规根轨迹的绘制法则4-3 广义根轨迹4-1 根轨迹法的基本概念一、根轨迹的概念根轨迹:系统中某个参数从零到无穷变化时,系统闭环特征根在s平面上移动的轨迹。
根指的是闭环特征根(闭环极点)。
根轨迹法是根据开环传递函数与闭环传递函数的关系,通过开环传递函数直接分析闭环特征根及系统性能的图解法。
K =0 s 1=0 s 2=-40 < K <1s 1 s 2为不等的负实根K =1s 1=-2 s 2=-21 < K < ∞s 1s2 实部均为-2由根轨迹可知:1)当K =0时,s 1=0,s 2=-1,这两点恰是开环传递函数的极点,同时也是闭环特征方程的极点.2)当0<K < 1 时,s 1,2都是负实根,随着k 的增长,s 1从s 平面的原点向左移,s 2从-1点向右移。
3) 当K = 1时, s 1,2= -2,两根重合在一起,此时系统恰好处在临界阻尼状态。
4) 1 <K <∞,s 1,2为共轭复根,它们的实部恒等于-2,虚部随着K 的增大而增大,系统此时为欠阻尼状态。
★在s平面上,用箭头标明K增大时,闭环特征根移动的方向,以数值表明某极点处的增益大小。
有了根轨迹图就可以分析系统的各种性能:(1)稳定性:根轨迹均在s的左半平面,则系统对所有K>0都是稳定的。
(2)稳态性能:如图有一个开环极点(也是闭环极点)s=0。
说明属于I型系统,阶跃作用下的稳态误差为0。
在速度信号V0t作用下,稳态误差为V0/K,在加速度信号作用下,稳态误差为∞。
(3)动态性能:过阻尼临界阻尼欠阻尼K越大,阻尼比ξ越小,超调量σ%越大。
由此可知:1、利用根轨迹可以直观的分析K的变化对系统性能的影响。
2、根据性能指标的要求可以很快确定出系统闭环特征根的位置;从而确定出可变参数的大小,便于对系统进行设计。
由以上分析知:根轨迹与系统性能之间有着密切的联系,但是,高阶方程很难求解,用直接解闭环特征根的办法来绘制根轨迹是很麻烦的。









31. K>0 系统总是稳定的。
2.0<K<0.5 不等实根,呈过阻尼状态3.K=0.5 系统呈临界阻尼状态。
4. K>0.5 呈欠阻尼状态。
5. K=1 最佳阻尼状态。
6. K>1 系统阻尼减弱,频率加大,平稳性变差。
7. 开环传递函数中有一个串联的积分环节,I 型,阶跃作用下的稳态误差为零;K v =K ,K 加大稳态精度提高。
可以得到闭环稳定性、过渡过程平稳性、稳态精度的全部信息。
根轨迹法由开环传递函数寻求闭环根轨迹。
K 05.01∞1s 2s 02−1−1−11⋅+−j 11⋅−−j ∞⋅+−j 1∞⋅−−j 1∞∞四、实轴上根轨迹所在区段内的右侧,开环零、∞∞(最小相位系统)8且τ>T例4-1 负反馈系统的开环传递函数)1()1()()(++=Ts s s K s H s G τ试确定K (由0→∞)变动下的系统根轨迹。
第一步:标出开环零、极点第二步:应用法则2阶系统有2条根轨迹,对称实轴;起于极点,终于零点及无穷远实轴上右侧零、极点数目之和为奇数例4-2 负反馈系统的开环传递函数试求系统闭环根轨迹的分离点d。
11例4-3图15例4-3图例4-3 负反馈系统的开环传递函数)15.0)(1()()(++=s s s Ks H s G 试作K (由0→∞)变动闭环根轨迹。
解:12312*0,1,2,,310.42, 1.58 20 60 3a a p p p d d s j k k πϕπσ==−=−⎧⎫=±⎨⎬⎩⎭=−=−=−=±==虚轴交点及及(舍)1618例4-4 单位负反馈系统的开环传递函数)5.15.0)(5.2()2)(5.1()(*j S s s j s s K s G ±++±++=试绘制K *(由0→∞)变动的系统根轨迹。
解:1920。
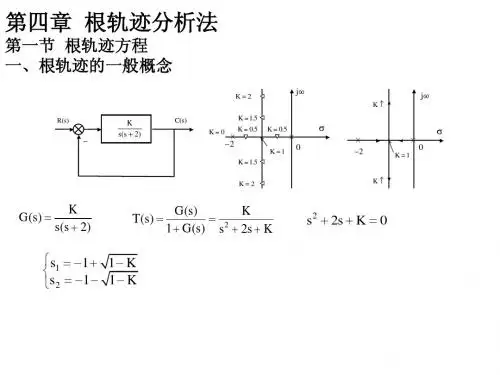
第四章 根轨迹法4-1 根轨迹的基本概念一. 根轨迹概念:闭环系统的动态性能与闭环极点在s 平面上的位置密切相关,系统的闭环极点也就是特征方程式的根.当系统的某一个或某些参量变化时,特征方程的根在s 平面上运动的轨迹称为根轨迹.根轨迹法: 直接由开环传递函数求取闭环特征根的方法.例: 设控制系统如图4-1所示()()15.0+=s s Ks G()()2220+=+=s s K s s K ,开环极点: 01=p , 22-=p ()()()0202K s s K s R s C s ++==Φ;式中K K 20= 此系统的特征方程式可写为:()02,1121102K s K s s s -±-=⇒=++=∆ 讨论: 200210-===s s K ,时,111210-=-==s s K ,时, j s j s K --=+-==112210,时, ∞--=∞+-=∞=j s j s K 11210,时,令k 为0 ∞.可以用解析的方法求出闭环极点的全部数值,将这些数值图4-1 控制系统的结构图R (s )C (s )K s(0.5s+1)标住在S 平面上,并连成光滑的粗实线,如图4-2所示。
图上,粗实线就称为系统的根轨迹。
分析:1.0K 变化时,根轨迹均位于左半s 平面,系统恒稳定.2.根轨迹有两条,两个起点2,021-==s s3.100<<K 时,闭环特征根为负实根,呈过阻尼状态.4.10=K 时,闭环特征根为一对重根,响应为单调上升的指数曲线.5.10>K 时,闭环特征根为共轭复根,响应为衰减振荡.6.开环增益K 可有根轨迹上对应的0K 值求得.0K 为可变参量绘制的根轨迹,称为常规根轨迹.二、根轨迹的幅值条件和相角条件设单闭环控制系统框图如图:通常有两种表示形式: A .时间常数形式:∏∏==++=ni imj j s T s K s H s G 11)1()1()()(τ图4-3 控制系统的结构图R (s )C (s )H(S)G(S)B .零、极点形式:∏∏==--=ni imj j p s z s K s H s G 110)()()()(则,系统特征方程:1+G(s)H(s)=0 ⇒ G(s)H(s)= -1 ⇒ 幅值条件: |G(s)H(s)|=1相角条件: ∠G(s)H(s)=±(2k+1)π, k=0,1,2,…考虑开环传递函数一般形式:∏∏==--=ni imj j p s z s K s H s G 110)()()()( ,因此幅值条件:1||||110=--∏∏==ni imj j ps z s K 或 ∏∏==--=mj jni izs p s K 110||||相角条件:)()(11∑∑==-∠--∠mj ni j jp s zs =±(2q+1)π, q=0,1,2,…说明:幅值条件与K 0有关,而相角条件与K 0无关。
因此,凡能满足相角条件的点必然满足幅值条件;而满足幅值条件的点不一定满足相角条件!因此,绘制根轨迹的一般步骤是:先找出S 平面上满足相角条件的点,并把它们连成曲线;然后根据实际需要,用幅值条件确定相关点对应的K 值。
例子:P107,例4-1。
4-2 绘制根轨迹的基本规则闭环特征方程:1)()(110-=--∏∏==ni imj j p s z s K上式表明了系统闭环极点和开环零、极点的关系。
基于这种关系,就可以根据开环零、极点的分布确定闭环极点的位置了。
根轨迹是根据系统的开环零、极点去绘制的。
在下面的讨论中,假定所研究的变化是根轨迹增益值K 0,但是当可变参数为系统的其他参数时,这些基本法则仍然适用。
这些基本法则绘出的根轨迹,其相角遵循 1800+2k π条件的称为1800 根轨迹;其相角遵循00+2k π条件的,称为00 根轨迹。
规则1:(对称性法则)根轨迹对称于S 平面的实轴。
规则2:根轨迹的分支数、根轨迹的起点和终点:分支数等于特征方程的阶数,为n 条;根轨从n 个开环极点出发,其中m 条终于开环零点,(n-m)条终点在无穷远处。
∏∏==--=mj jini zs p s K 110||||, K 0=0为根轨迹的起点 s = p i∏∏==--=n i imj jps zs K 110||||1, K 0→∞为根轨迹的终点j 或s →∞规则3:根轨迹在实轴上分布:实轴上某线段右边的实零点和实极点总数为奇数时, 这些线段就是根轨迹的部分。
规则4:根轨迹的渐进线n-m 条趋向无穷远的根轨迹可由渐进线决定:渐进线的倾角为: ,2,1,0)12(=-+±=q mn q a πϕ渐进线与实轴的交点为:开环零点数开环极点数开环零点的实部之和开环极点的实部之和--=--=∑∑==mn zp n i mj ji a 11σ例1:设控制系统的开环传递函数为)22)(3()2(3)()(2++++=s s s s s K s H s G ,求渐进线和与实轴的交点。
解 (1)系统的开环极点为0,-3,(-1+j )和(-1-j ),它们是根轨迹上各分支的起点。
共有四条根轨迹分支。
有一条根轨迹分支终止在有限开环零点-2,其它三条根轨迹分支将趋向于无穷远处。
(2)确定根轨迹的渐近线 渐近线的倾斜角为14180)12()12(-︒⨯+=-+=q m n q a πϕ 取式中的q =0,1,2,得φa =π/3,π,5π/3,或±60°及-180°。
渐近线与实轴的交点为114)2()1130(111-=-----+--=⎥⎦⎤⎢⎣⎡--=∑∑==j j z p m n m i i nj j a σ规则5:根轨迹的分离点、会合点、分离角:两条以上根轨迹的交点。
分离点和会合点必须满足方程00=dsdK ----必要条件 分离角----根轨迹离开重极点处的切线与实轴正方向的夹角分离角=rq π)12(+ , r 为重根数,q=0,1,2… 例2:已知控制系统的开环传递函数为)164)(1()1()()(20++-+=s s s s s K s H s G ,确定根轨迹的分离点。
解 :系统的特征方程式为:0)1()164)(1(02=++++-s K s s s s即:1)164)(1(20+++--=s s s s s K利用0/0=ds dK ,则有0)1(16242110322340=+-+++-=s s s s s ds dK 解之可得,分离点d 1=0.46 和 d 2=-2.22。
规则6:根轨迹的出射角和入射角:出射角:从复数极点出发的角度。
入射角:到达复数零点的角度。
P116, 图4-13:取靠近4P 的点i s ,由相角条件:()()()()()() ,,,,2101243211=+=-∠--∠--∠--∠--∠q q p s p s p s p s z s i i i i i π 4p s i →时,则:()()()()()()143424144412z p p p p p p p q p s i p -∠+-∠--∠--∠-+=-∠=πθ一般情况,出射角:()()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-∠--∠+=∑∑≠==nk i i i k m j j k pkp p z p 11πθ同理,入射角:()()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-∠--∠-=∑∑=≠=ni i k m k j j j k zkp z z z 11πθ规则7:根轨迹与虚轴的交点两种方法: (1).用劳斯判据求(2).将ωj s =带入特征方程求解例3:设系统的开环传递函数为:)2)(1(2)()(++=s s s Ks H s G ,试绘制系统的根轨迹。
解 根据绘制根轨迹的法则,先确定根轨迹上的一些特殊点,然后绘制其根轨迹图。
(1)系统的开环极点为0,1-,2-是根轨迹各分支的起点。
由于系统没有有限开环零点,三条根轨迹分支均趋向于无穷远处。
(2)系统的根轨迹有3=-m n 条渐进线渐进线的倾斜角为3180)12()12(-︒⨯+=-+=q m n q a πϕ 取式中的q =0,1,2,得φa =π/3,π,5π/3。
渐进线与实轴的交点为: 13)210(111-=--=⎥⎦⎤⎢⎣⎡--=∑∑==m i i nj j a z p m n σ 三条渐近线如图4-13中的虚线所示。
(3)实轴上的根轨迹位于原点与-1点之间以及-2点的左边,如图的粗实线所示。
(4)确定分离点: 系统的特征方程式为:022323=+++K s s s即:)23(2123s s s K ++-= 利用0/=ds dK ,则有:0)26(2123=++-=s s ds dK解得:423.01-=s 和 577.12-=s由于在-1到-2之间的实轴上没有根轨迹,故s 2=-1.577显然不是所要求的分离点。
因此,两个极点之间的分离点应为s 1=-0.423。
(5)确定根轨迹与虚轴的交点 方法一 利用劳斯判据确定劳斯行列表为 3s 1 2 2s32K 1s326K-s2K由劳斯判据,系统稳定时K 的极限值为3。
相应于K =3的频率可由辅助方程0632322=+=+s K s 确定。
解之得根轨迹与虚轴的交点为2j s ±=。
根轨迹与虚轴交点处的频率为41.12±=±=ω方法二 令ωj s =代入特征方程式,可得:02)(2)(3)(23=+++K j j j ωωω 即:0)2()32(22=-+-ωωωj K令上述方程中的实部和虚部分别等于零,即:0322=-ωK ,022=-ωω 所以 :2±=ω 3=K 系统的根轨迹如图所示:规则8:闭环极点的和与积.系统特征方程(n>m 时)为 闭环极点的和:()开环极点之和和∑==ni i p 1闭环极点的积:()()∏∏==+=mj i ni i z K p 101积可利用此性质判闭环极点i s 的分布情况 一些i s 变化后,另一些i s 会做相反变化.例4:在例3中,确定根轨迹各分支上每一点的K 值S 平面σωj根据绘制根轨迹的基本法则,当从开环极点0与-1出发的两条根轨迹分支向右运动时,从另一极点-2出发的根轨迹分支一定向左移动。
当前两条根轨迹分支和虚轴在K =3处相交时,可按式3)41.10()41.10(-=-+++j j x σ(开环极点0,-1,-2之和;即和为定值)求出后一条根轨迹分支上K =3的点为οx =-3。
由(4)知,前两条根轨迹分支离开实轴时的相应根值为-0.423±j 0。
因此,后一条根轨迹分支的相应点为3)423.0()423.0(-=-+-+x σ所以 ,οx =-2.154。