第五章线性定常系统的综合

现代控制理论习题《现代控制理论》练习题判断题1. 由⼀个状态空间模型可以确定惟⼀⼀个传递函数。

3. 对⼀个给定的状态空间模型，若它是状态能控的，则也⼀定是输出能控的。

4. 对系统Ax x= ，其Lyapunov 意义下的渐近稳定性和矩阵A 的特征值都具有负实部是⼀致的。

5. 对⼀个系统，只能选取⼀组状态变量；6. 由状态转移矩阵可以决定系统状态⽅程的系统矩阵，进⽽决定系统的动态特性；7. 状态反馈不改变系统的能控性。

8. 若传递函数B A sI C s G 1)()(--=存在零极相消，则对应状态空间模型描述的系统是不能控的；9. 若线性系统是李雅普诺夫意义下稳定的，则它是⼤范围渐近稳定的；10. 相⽐于经典控制理论，现代控制理论的⼀个显著优点是可以⽤时域法直接进⾏系统的分析和设计。

11. 传递函数的状态空间实现不唯⼀的⼀个主要原因是状态变量选取不唯⼀。

12. 状态变量是⽤于完全描述系统动态⾏为的⼀组变量，因此都是具有物理意义。

13. 等价的状态空间模型具有相同的传递函数。

14. 互为对偶的状态空间模型具有相同的能控性。

15. ⼀个系统的平衡状态可能有多个，因此系统的李雅普诺夫稳定性与系统受扰前所处的平衡位置⽆关。

16. 若⼀线性定常系统的平衡状态是渐近稳定的，则从系统的任意⼀个状态出发的状态轨迹随着时间的推移都将收敛到该平衡状态。

17. 反馈控制可改变系统的稳定性、动态性能，但不改变系统的能控性和能观性。

18. 如果⼀个系统的李雅普诺夫函数确实不存在，那么我们就可以断定该系统是不稳定的。

填空题l ．系统状态完全能控是指。

2．系统状态的能观性是指。

3．系统的对偶原理：。

4．对于⼀个不能控和不能观的系统，按系统结构标准分解为、、、、的四个⼦系统。

5．对于单输⼊单输出系统，系统能控、能观的充要条是是。

7．系统平衡状态的渐近稳定性的定义为：。

10．受控系统∑),,(C B A ，采⽤状态反馈能镇定的充分必要条件是。

《现代控制理论》课程教学大纲课程名称：现代控制理论课程类别：任意选修课适用专业：电子信息工程考核方式：考查总学时、学分：24学时1.5学分一、课程性质、教学目标《现代控制理论》是在“古典控制理论”的基础上，基于“线性代数”理论发展起来的一种自动控制系统性能分析与设计的新方法。

它由“古典控制理论”中的对单输入单输出系统的描述过渡到对多输入多输出系统的描述、由“古典控制理论”中对系统的外部性能分析过渡到内部性能分析、由“古典控制理论”中便于手工求解的数学模型过渡到便于计算机求解的数学模型。

为学生后续深造的课程《线性系统理论及应用》、《智能控制系统及应用》的学习打下必要的理论知识和实践基础。

其具体的课程教学目标为：课程教学目标1：掌握控制系统数学模型含义，系统数学模型的类型及相互关系，并能够建立常用线性系统的数学模型。

课程教学目标2：掌握线性控制系统状态方程的求解方法。

课程教学目标3：掌握控制系统的能控性和能观测性判据，并利用判据判断系统的能控性和能观测性。

通过本课程的学习,使学生掌握有关运用状态空间分析法定量和定性分析及综合控制系统的基本理论、基本方法,为学习后续课程打下基础。

三、先修课程高等数学、大学物理、电路分析、模拟电路、数字电路、高频电路、信号与系统、线性代数、自动控制原理。

四、课程教学重、难点教学重点：控制系统数学模型的建立，线性控制系统的运动能控性与能观测性和稳定性分析，线性定常系统的综合；教学难点：线性定常系统的综合。

五、课程教学方法与教学手段教学方法：讲授式教学方法、讨论式教学方法、导学式教学方法；教学手段：多媒体辅助教学。

六、课程教学内容绪论（1学时）1．教学内容(1) 自动控制与控制理论；(2) 控制理论发展简况；(3) 现代控制理论的基本内容；(4) 本课程的基本任务。

2．重、难点提示(1) 重点是控制理论的基本内容、本课程的基本任务；(2) 难点是控制理论的基本内容。

第一章控制系统的数学模型（5学时）1．教学内容(1) 状态空间表达式；(2) 由微分方程求状态空间表达式；(3) 传递函数矩阵；(4) 离散系统的数学描述；(5) 线性变换；(6) 组合系统的数学描述；(7) 利用MATLAB进行模型的转换。

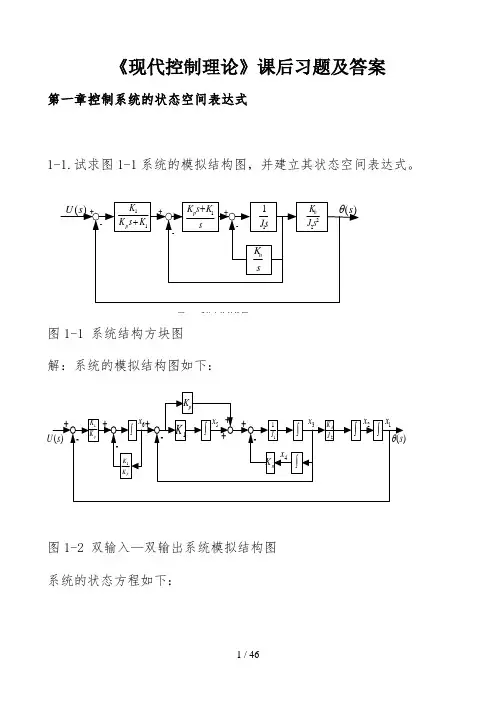
《现代控制理论》课后习题及答案第一章控制系统的状态空间表达式1-1.试求图1-1系统的模拟结构图，并建立其状态空间表达式。

图1-27系统方块结构图图1-1 系统结构方块图解：系统的模拟结构图如下：图1-30双输入--双输出系统模拟结构图图1-2 双输入—双输出系统模拟结构图系统的状态方程如下：u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n p b1611166131534615141313322211+--=+-==++--===••••••令y s =)(θ，则1x y =所以，系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡••••••6543211654321111111126543210000010000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp n p b1-2.有电路如图1-3所示。

以电压)(t u 为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻2R 上的电压作为输出量的输出方程。

U图1-28 电路图图1-3 电路图解：由图，令32211,,x u x i x i c===，输出量22x R y =有电路原理可知：•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为：[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。

自动控制原理发布日期:2011-8-27 15:29:51新闻来自:本站原创考试内容包括古典控制理论（不包含采样控制系统和非线性部分）与现代控制理论（只包含三章的内容）两部分，古典控制理论内容占70%，现代控制理论内容占30%。

古典控制理论部分第一章绪论1. 掌握自动控制系统的工作原理、自动控制系统的组成与几种不同分类。

2. 重点掌握反馈的概念、基本控制方式、对控制系统的基本要求。

第二章线性系统的数学模型控制理论的两大任务是系统分析与系统设计，系统分析和设计中首先要建立被研究系统的数学模型。

本章主要给出古典控制理论使用的系统数学模型——传递函数的建立。

本章要求：1．掌握的概念：传递函数；极点、零点；开环传递函数、闭环传递函数、误差传递函数；典型环节的传递函数。

2．掌握建立电气系统、机械系统的微分方程和传递函数模型的方法。

3．重点掌握方框图化简或信号流图梅森增益公式获得系统传递函数的建模方法。

第三章控制系统时域分析根据研究系统采用的不同数学模型，分析方法是不同的，本章给出利用系统传递函数数学模型求取时间响应的系统时域分析法。

主要是分析系统的三大基本性能，即系统的稳（稳定性）、准（准确性）、快（快速性）。

稳定性是系统工作的必要条件；快速性和相对稳定程度（振荡幅度）是评价系统动态响应的性能指标；准确性是指系统稳态响应的稳态精度，用稳态误差来衡量，需注意：讨论的稳态误差是指由输入信号和系统结构引起的系统稳态时的误差。

本章要求：1．掌握的概念：稳定性；动态（或暂态）性能指标（最大超调量、上升时间、峰值时间、调整时间）；稳态（静态）性能指标（稳态误差）；一阶、二阶系统的主要特征参量；欠阻尼、临界阻尼、过阻尼系统特点；主导极点。

2．重点掌握系统稳定性判别（Routh判据）；稳态误差终值计算（包括三个稳态误差系数的计算）；二阶系统动态性能指标计算。

3．掌握利用主导极点对高阶系统模型的简化与性能分析。

第四章根轨迹法闭环系统特征方程的根（系统闭环极点）在S平面的分布完全决定了系统的稳定性、主要决定了系统的动态性能，因此利用根轨迹（闭环系统特征方程的根随系统参数变化在S平面所形成的轨迹）可对系统性能进行分析。

《现代控制理论》习题第一章 控制系统的状态空间模型1.1 考虑以下系统的传递函数：656)()(2+++=s s s s U s Y试求该系统状态空间表达式的能控标准形和可观测标准形。

1.2 考虑下列单输入单输出系统：u y y yy 66116=+++试求该系统状态空间表达式的对角线标准形。

1.3 考虑由下式定义的系统：Cxy Bu Ax x=+=式中]11[,213421=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=C B A ，－－试将该系统的状态空间表达式变换为能控标准形。

1.4 考虑由下式定义的系统：Cxy Bu Ax x=+=式中]011[,10030021101=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=C B A ，－－试求其传递函数Y(s)/U(s)。

1.5 考虑下列矩阵：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=0001100001000010A试求矩阵A 的特征值λ1,λ2,λ3 和λ4。

再求变换矩阵P ，使得),,,(diag 43211λλλλ=-AP P第二章 状态方程的解2.1 用三种方法计算下列矩阵A 的矩阵指数函数At e 。

1） ⎥⎦⎤⎢⎣⎡--=5160A； 2） ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=6116100010A2.2 计算下列矩阵的矩阵指数函数At e 。

1） ⎥⎦⎤⎢⎣⎡=0010A ； 2） ⎥⎦⎤⎢⎣⎡=1002－－A ； 3） ⎥⎦⎤⎢⎣⎡-=0110A ； 4） ⎥⎦⎤⎢⎣⎡=1021A5) ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=200010011A ； 6） ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=210010001A ； 7） ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=000100010A2.2 给定线性定常系统Ax x=式中⎥⎦⎤⎢⎣⎡--=2310A且初始条件为⎥⎦⎤⎢⎣⎡-=11)0(x试求该齐次状态方程的解x (t )。

2.4 已知系统方程如下[]xy u x x 11015610-=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=求输入和初值为以下值时的状态响应和输出响应。