三角形全等之手拉手模型、倍长中线、截长补短法、旋转、寻找三角形全等方法归纳总结

全等模型-倍长中线与截长补短模型全等三角形在中考数学几何模块中占据着重要地位，也是学生必须掌握的一块内容，本专题就全等三角形中的重要模型（倍长中线模型、截长补短模型）进行梳理及对应试题分析，方便掌握。

模型1.倍长中线模型【模型解读】中线是三角形中的重要线段之一，在利用中线解决几何问题时，常常采用“倍长中线法”添加辅助线．所谓倍长中线法，就是将三角形的中线延长一倍，以便构造出全等三角形，从而运用全等三角形的有关知识来解决问题的方法．（注：一般都是原题已经有中线时用，不太会有自己画中线的时候）。

【常见模型及证法】1、基本型：如图1，在三角形ABC 中，AD 为BC 边上的中线.证明思路：延长AD 至点E ，使得AD =DE . 若连结BE ，则BDE CDA ∆≅∆；若连结EC ，则ABD ECD ∆≅∆；2、中点型:如图2，C 为AB证明思路：若延长EC 至点F ，使得CF EC =，连结AF ，则BCE ACF ∆≅∆;若延长DC 至点G ，使得CG DC =，连结BG ，则ACD BCG ∆≅∆.3、中点+平行线型：如图3, //AB CD ，点E 为线段AD 的中点.证明思路：延长CE 交AB 于点F (或交BA 延长线于点F )，则EDC EAF ∆≅∆.例1．（2023·江苏徐州·模拟预测）（1）阅读理解：如图①，在ABC 中，若8AB =，5AC =，求BC 边上的中线AD 的取值范围．可以用如下方法：将ACD △绕着点D 逆时针旋转180︒得到EBD △，在ABE △中，利用三角形三边的关系即可判断中线AD 的取值范围是______；（2）问题解决：如图②，在ABC 中，D 是BC 边上的中点，DE DF ⊥于点D ，DE 交AB 于点E ，DF 交AC 于点F ，连接EF ，求证：BE CF EF +>；（3）问题拓展：如图③，在四边形ABCD 中，180B D ∠+∠=︒，CB CD =，100BCD ∠=︒，以C 为顶点作一个50︒的角，角的两边分别交AB 、AD 于E 、F 两点，连接EF ，探索线段BE ，DF ，EF 之间的数量关系，并说明理由．【答案】（1）31322AD <<；（2）见详解；（3）EF BE DF =+，理由见详解【分析】（1）根据旋转的性质可证明ADC EDB ≅，6,AC BE AD ED ===，在ABE △中根据三角形三边关系即可得出答案；（2）延长FD 至M ，使DF=DM ，连接BM ，EM ，可得出CF BM =，根据垂直平分线的性质可得出EF EM =，利用三角形三边关系即可得出结论；（3）延长AB 至N ，使BN=DF ，连接CN ，可得NBC D ∠=∠，证明NBC FDC ≅，得出,CN CF NCB FCD =∠=∠，利用角的和差关系可推出50ECN ECF ∠=︒=，再证明NCE FCE ≅，得出EN EF =，即可得出结论．【详解】解：（1）∵,,AD ED CD BD ADC BDE ==∠=∠∴ADC EDB ≅∴5,AC BE AD ED ===在ABE △中根据三角形三边关系可得出：AB BE AE AB BE −<<+，即3213AD << ∴31322AD <<故答案为：31322AD <<； （2）延长FD 至M ，使DF=DM ，连接BM ，EM ，同（1）可得出CF BM =，∵,FD MD FD DE =⊥∴EF EM =在BEM △中，BE BM EM +>∴BE CF EF +>；（3）EF BE DF =+，理由如下：延长AB 至N ，使BN=DF ，连接CN ，∵180,180ABC D ABC NBC ∠+∠=︒∠+∠=︒∴NBC D ∠=∠∴NBC FDC ≅∴,CF CN NCB FCD =∠=∠∵100,50BCD FCE ∠=︒∠=︒∴50ECN ECF ∠=︒=∴NCE FCE ≅（SAS ）∴EN EF =∴EF EN BE BN BE DF ==+=+∴EF BE DF =+．【点睛】本题考查的知识点有旋转的性质、全等三角形的判定及性质、线段垂直平分线的性质、三角形三边关系、角的和差等，解答此题的关键是作出辅助线，构造出与图①中结构相关的图形．此题结构精巧，考查范围广，综合性强．例2．（2023·贵州毕节·二模）课外兴趣小组活动时，老师提出了如下问题：(1)如图1，△ABC 中，若AB =5，AC =3，求BC 边上的中线AD 的取值范围．小明在组内经过合作交流，得到了如下的解决方法：延长AD 到点E ，使DE =AD ，请根据小明的方法思考帮小明完成解答过程．(2)如图2，AD 是△ABC 的中线，BE 交AC 干E ，交AD 于F ，且AE =EF ．请判昕AC 与BF 的数量关系，并说明理由．【答案】(1)见解析(2)AC=BF ，理由见解析【解析】（1）解：如图，延长AD 到点E ，使DE=AD ，连接BE ，在△ADC 和△EDB 中∵AD DE ADC EDB CD DB =⎧⎪∠=∠⎨⎪=⎩，∴△ADC ≌△EDB （SAS ）．∴BE=AC=3．∵AB -BE<AE<AB+BE ∵2<AE<8．∵AE=2AD ∴1<AD<4．（2）AC=BF ，理由如下：延长AD 至点G ，使GD=AD ，连接BG ，在△ADC 和△GDB 中，AD DG ADC GDB BD CD =⎧⎪∠=∠⎨⎪=⎩，∴△ADC ≌△GDB （SAS ）．∴BG=AC ，∠G=∠DAC ．．∵AE=EF ∴∠AFE=∠FAE ． ∴∠DAC=∠AFE=∠BFG ∴∠G=∠BFG ∴BG=BF ∴AC=BF ．【点睛】本题考查全等三角形判定与性质，三角形三边的关系，作辅助线：延长AD 到点E ，使DE=AD ，构造全等三角形是解题的关键．例3．（2022·山东·安丘市一模）阅读材料：如图1，在ABC 中，D ，E 分别是边AB ，AC 的中点，小亮在证明“三角形的中位线平行于第三边，且等于第三边的一半”时，通过延长DE 到点F ，使EF DE =，连接CF ，证明ADE CFE ≌，再证四边形DBCF 是平行四边形即得证．类比迁移：（1）如图2，AD 是ABC 的中线，E 是AC 上的一点，BE 交AD 于点F ，且AE EF =，求证：AC BF =． 小亮发现可以类比材料中的思路进行证明．证明：如图2，延长AD 至点M ，使MD FD =，连接MC ，……请根据小亮的思路完成证明过程．方法运用：（2）如图3，在等边ABC 中，D 是射线BC 上一动点（点D 在点C 的右侧），连接AD ．把线段CD 绕点D 逆时针旋转120°得到线段DE ，F 是线段BE 的中点，连接DF 、CF ．请你判断线段DF 与AD 的数量关系，并给出证明．【答案】（1）证明见解析；（2）2AD DF =，证明见解析【分析】(1) 延长AD 至M ，使MD FD =，连接MC ，证明BDF CDM △≌△，结合等角对等边证明即可． (2) 延长DF 至点M ，使DF FM =，连接BM 、AM ，证明(SAS)ABM ACD △≌△，△ABM 是等边三角形，代换后得证．【详解】（1）证明：延长AD 至M ，使MD FD =，连接MC ．在BDF 和CDM V 中，BD CD BDF CDM DF DM =⎧⎪∠=∠⎨⎪=⎩，∴BDF CDM △≌△，∴MC BF =，M BFM ∠=∠， ∵AE EF =，∴EAF EFA ∠=∠，∵EFA BFM ∠=∠，∴M MAC ∠=∠，∴AC MC =，∴AC BF =．（2）线段DF 与AD 的数量关系为：2AD DF =．证明如下：延长DF 至点M ，使DF FM =，连接BM 、AM ，如图2所示：∵点F 为BE 的中点，∴BF EF =在BFM 和EFD △中，∵BF EF BFM EFD FM DF =⎧⎪∠=∠⎨⎪=⎩，∴(SAS)BFM EFD △≌△∴BM DE =，MBF DEF ∠=∠，∴BM DE ∥ ∵线段CD 绕点D 逆时针旋转120°得到线段DE∴CD DE BM ==，120∠=︒BDE ，∴18012060MBD ∠=−=︒︒︒∵ABC 是等边三角形∵AB AC =，60ABC ACB ∠=∠=︒，∴6060120ABM ABC MBD ∠∠∠︒︒=+=+=︒ ∵180********ACD ACB ∠=︒−∠=︒−︒=︒，∴ABM ACD ∠=∠在ABM 和ACD △中，∵AB AC ABM ACD BM CD =⎧⎪∠=∠⎨⎪=⎩，∴(SAS)ABM ACD △≌△∴AM AD =，BAM CAD ∠=∠，∴60MAD MAC CAD MAC BAM BAC ∠∠∠∠∠∠=+=+==︒∴AMD 是等边三角形，∴2==AD DM DF ．【点睛】本题考查了等边三角形的判定和性质，三角形全等的判定和性质，熟练掌握等边三角形的判定和性质，三角形全等的判定和性质是解题的关键．例4．（2022·河南商丘·一模）阅读材料如图1，在△ABC 中，D ，E 分别是边AB ，AC 的中点，小明在证明“三角形的中位线平行于第三边，且等于第三边的一半”时，通过延长DE 到点F ，使EF ＝DE ，连接CF ，证明△ADE ≌△CFE ，再证四边形DBCF 是平行四边形即得证．(1)类比迁移：如图2，AD 是△ABC 的中线，BE 交AC 于点E ，交AD 于点F ，且AE ＝EF ，求证：AC ＝BF ． 小明发现可以类比材料中的思路进行证明．证明：如图2，延长AD 至点M ，使MD ＝FD ，连接MC ，……请根据小明的思路完成证明过程．(2)方法运用：如图3，在等边△ABC 中，D 是射线BC 上一动点（点D 在点C 的右侧），连接AD ．把线段CD 绕点D 逆时针旋转120°得到线段DE ．F 是线段BE 的中点，连接DF ，CF ．请你判断线段DF 与AD 的数量关系，并给出证明；【答案】(1)见解析(2)线段DF 与AD 的数量关系为：AD ＝2DF ，证明见解析；【分析】（1）类比材料，运用倍长中线辅助线作法，证得结论．（2）运用倍长中线辅助线作法，结合三角形全等证明及等边三角形性质，得出结论．（1）证明：如图，延长AD 至M ，使MD ＝FD ，连接MC ，在△BDF 和△CDM 中，∵BD CD BDF CDM DF DM =⎧⎪∠=∠⎨⎪=⎩，∴△BDF ≌△CDM （SAS ），∴MC ＝BF ，∠M ＝∠BFM ，∵AE ＝EF ，∴∠EAF ＝∠EFA ，∵∠EFA＝∠BFM，∴∠M＝∠MAC，∴AC＝MC，∴AC＝BF；（2）解：线段DF与AD的数量关系为：AD＝2DF，证明如下：延长DF至点M，使DF＝FM，连接BM、AM，如图所示：∵点F为BE的中点，∴BF＝EF，在△BFM和△EFD中，∵BF EFBFM EFDFM DF=⎧⎪∠=∠⎨⎪=⎩，∴△BFM≌△EFD（SAS），∴BM＝DE，∠MBF＝∠DEF，∴BM∥DE，∵线段CD绕点D逆时针旋转120°得到线段DE，∴CD＝DE＝BM，∠BDE＝120°，∴∠MBD＝180°﹣120°＝60°，∵△ABC是等边三角形，∴AB＝AC，∠ABC＝∠ACB＝60°，∴∠ABM＝∠ABC+∠MBD＝60°+60°＝120°，∵∠ACD＝180°﹣∠ACB＝180°﹣60°＝120°，∴∠ABM＝∠ACD，在△ABM和△ACD中，∵AB ACABM ACDBM CD=⎧⎪∠=∠⎨⎪=⎩，∴△ABM≌△ACD（SAS），∴AM＝AD，∠BAM＝∠CAD，∴∠MAD＝∠MAC+∠CAD＝∠MAC+∠BAM＝∠BAC＝60°，∴△AMD是等边三角形，∴AD＝DM＝2DF；综合运用相关知识是解题的关键．模型2.截长补短模型【模型解读】截长补短的方法适用于求证线段的和差倍分关系。

专题13全等模型-倍长中线与截长补短模型全等三角形在中考数学几何模块中占据着重要地位，也是学生必须掌握的一块内容，本专题就全等三角形中的重要模型（倍长中线模型、截长补短模型）进行梳理及对应试题分析，方便掌握。

模型1.倍长中线模型【模型解读】中线是三角形中的重要线段之一，在利用中线解决几何问题时，常常采用“倍长中线法”添加辅助线．所谓倍长中线法，就是将三角形的中线延长一倍，以便构造出全等三角形，从而运用全等三角形的有关知识来解决问题的方法．（注：一般都是原题已经有中线时用，不太会有自己画中线的时候）。

【常见模型及证法】1、基本型：如图1，在三角形ABC 中，AD 为BC 边上的中线.证明思路：延长AD 至点E ，使得AD =DE .若连结BE ，则BDE CDA ；若连结EC ，则ABD ECD ；2、中点型:如图2，C 为AB 的中点.证明思路：若延长EC 至点F ，使得CF EC ，连结AF ，则BCE ACF ;若延长DC 至点G ，使得CG DC ，连结BG ，则ACD BCG .3、中点+平行线型：如图3,//AB CD ，点E 为线段AD 的中点.证明思路：延长CE 交AB 于点F (或交BA 延长线于点F )，则EDC EAF .例1．（2023·江苏徐州·模拟预测）（1）阅读理解：如图①，在ABC 中，若8AB ，5AC ，求BC 边上的中线AD 的取值范围．可以用如下方法：将ACD △绕着点D 逆时针旋转180 得到EBD △，在ABE △中，利用三角形三边的关系即可判断中线AD 的取值范围是______；（2）问题解决：如图②，在ABC 中，D 是BC 边上的中点，DE DF 于点D ，DE 交AB 于点E ，DF 交AC 于点F ，连接EF ，求证：BE CF EF ；（3）问题拓展：如图③，在四边形ABCD 中，180B D ，CB CD ，100BCD ，以C 为顶点作一个50 的角，角的两边分别交AB 、AD 于E 、F 两点，连接EF ，探索线段BE ，DF ，EF 之间的数量关系，并说明理由．同（1）可得出CF BM ，∵,FD MD FD DE ∴EF EMEF ；（3）EF BE DF ，理由如下：延长AB 至N ，使BN=DF ，连接CN ，∵180,180ABC D ABC NBC ∴NBC D∴NBC FDC ∴,CF CN NCB FCD∵100,50BCD FCE ∴50ECN ECF∴NCE FCE （SAS ）∴EN EF∴EF EN BE BN BE DF ∴EF BE DF ．【点睛】本题考查的知识点有旋转的性质、全等三角形的判定及性质、线段垂直平分线的性质、三角形三边关系、角的和差等，解答此题的关键是作出辅助线，构造出与图①中结构相关的图形．此题结构精巧，考查范围广，综合性强．例2．（2023·贵州毕节·二模）课外兴趣小组活动时，老师提出了如下问题：(1)如图1，△ABC 中，若AB =5，AC =3，求BC 边上的中线AD 的取值范围．小明在组内经过合作交流，得到了如下的解决方法：延长AD 到点E ，使DE =AD ，请根据小明的方法思考帮小明完成解答过程．(2)如图2，AD 是△ABC 的中线，BE 交AC 干E ，交AD 于F ，且AE =EF ．请判昕AC 与BF 的数量关系，并说明理由．【答案】(1)见解析(2)AC =BF ，理由见解析【解析】（1）解：如图，延长AD 到点E ，使DE =AD ，连接BE ，在△ADC 和△EDB 中∵AD DE ADC EDB CD DB，∴△ADC ≌△EDB （SAS ）．∴BE =AC =3．∵AB -BE <AE <AB +BE ∵2<AE <8．∵AE =2AD ∴1<AD <4．（2）AC=BF，理由如下：延长AD至点G，使GD=AD，连接BG，在△ADC和△GDB中，AD DGADC GDBBD CD，∴△ADC≌△GDB（SAS）．∴BG=AC，∠G=∠DAC．．∵AE=EF∴∠AFE=∠FAE．∴∠DAC=∠AFE=∠BFG∴∠G=∠BFG∴BG=BF∴AC=BF．【点睛】本题考查全等三角形判定与性质，三角形三边的关系，作辅助线：延长AD到点E，使DE=AD，构造全等三角形是解题的关键．例3．（2022·山东·安丘市一模）阅读材料：如图1，在ABC中，D，E分别是边AB，AC的中点，小亮在证明“三角形的中位线平行于第三边，且等于第三边的一半”时，通过延长DE到点F，使EF DE，连接CF，证明ADE CFE≌，再证四边形DBCF是平行四边形即得证．类比迁移：（1）如图2，AD是ABC的中线，E是AC上的一点，BE交AD于点F，且AE EF，求证：AC BF．小亮发现可以类比材料中的思路进行证明．证明：如图2，延长AD至点M，使MD FD，连接MC，……请根据小亮的思路完成证明过程．方法运用：（2）如图3，在等边ABC中，D是射线BC上一动点（点D在点C的右侧），连接AD．把线段CD绕点D逆时针旋转120°得到线段DE，F是线段BE的中点，连接DF、CF．请你判断线段DF与AD 的数量关系，并给出证明．【答案】（1）证明见解析；（2）2AD DF ，证明见解析【分析】(1)延长AD 至M ，使MD FD ，连接MC ，证明BDF CDM △≌△，结合等角对等边证明即可．(2)延长DF 至点M ，使DF FM ，连接BM 、AM ，证明(SAS)ABM ACD △≌△，△ABM 是等边三角形，代换后得证．【详解】（1）证明：延长AD 至M ，使MD FD ，连接MC ．在BDF 和CDM V 中，BD CD BDF CDM DF DM，∴BDF CDM △≌△，∴MC BF ，M BFM ，∵AE EF ，∴EAF EFA ，∵EFA BFM ，∴M MAC ，∴AC MC ，∴AC BF ．（2）线段DF 与AD 的数量关系为：2AD DF ．证明如下：延长DF 至点M ，使DF FM ，连接BM 、AM ，如图2所示：∵点F 为BE 的中点，∴BF EF在BFM 和EFD △中，∵BF EF BFM EFD FM DF，∴(SAS)BFM EFD △≌△∴BM DE ，MBF DEF ，∴BM DE ∥∵线段CD 绕点D 逆时针旋转120°得到线段DE ∴CD DE BM ，120 BDE ，∴18012060MBD∵ABC 是等边三角形∵AB AC ，60ABC ACB ，∴6060120ABM ABC MBD ∵180********ACD ACB ，∴ABM ACD在ABM 和ACD △中，∵AB AC ABM ACD BM CD，∴(SAS)ABM ACD △≌△∴AM AD ，BAM CAD ，∴60MAD MAC CAD MAC BAM BAC ∴AMD 是等边三角形，∴2 AD DM DF ．【点睛】本题考查了等边三角形的判定和性质，三角形全等的判定和性质，熟练掌握等边三角形的判定和性质，三角形全等的判定和性质是解题的关键．例4．（2022·河南商丘·一模）阅读材料如图1，在△ABC中，D，E分别是边AB，AC的中点，小明在证明“三角形的中位线平行于第三边，且等于第三边的一半”时，通过延长DE到点F，使EF＝DE，连接CF，证明△ADE≌△CFE，再证四边形DBCF是平行四边形即得证．(1)类比迁移：如图2，AD是△ABC的中线，BE交AC于点E，交AD于点F，且AE＝EF，求证：AC＝BF．小明发现可以类比材料中的思路进行证明．证明：如图2，延长AD至点M，使MD＝FD，连接MC，……请根据小明的思路完成证明过程．(2)方法运用：如图3，在等边△ABC中，D是射线BC上一动点（点D在点C的右侧），连接AD．把线段CD绕点D逆时针旋转120°得到线段DE．F是线段BE的中点，连接DF，CF．请你判断线段DF与AD的数量关系，并给出证明；【答案】(1)见解析(2)线段DF与AD的数量关系为：AD＝2DF，证明见解析；【分析】（1）类比材料，运用倍长中线辅助线作法，证得结论．（2）运用倍长中线辅助线作法，结合三角形全等证明及等边三角形性质，得出结论．（1）证明：如图，延长AD至M，使MD＝FD，连接MC，在△BDF和△CDM中，∵BD CDBDF CDMDF DM，∴△BDF≌△CDM（SAS），∴MC＝BF，∠M＝∠BFM，∵AE＝EF，∴∠EAF＝∠EFA，∵∠EFA＝∠BFM，∴∠M＝∠MAC，∴AC＝MC，∴AC＝BF；（2）解：线段DF与AD的数量关系为：AD＝2DF，证明如下：延长DF至点M，使DF＝FM，连接BM、AM，如图所示：∵点F为BE的中点，∴BF＝EF，在△BFM和△EFD中，∵BF EFBFM EFDFM DF，∴△BFM≌△EFD（SAS），∴BM＝DE，∠MBF＝∠DEF，∴BM∥DE，∵线段CD绕点D逆时针旋转120°得到线段DE，∴CD＝DE＝BM，∠BDE＝120°，∴∠MBD＝180°﹣120°＝60°，∵△ABC是等边三角形，∴AB＝AC，∠ABC＝∠ACB＝60°，∴∠ABM＝∠ABC+∠MBD＝60°+60°＝120°，∵∠ACD＝180°﹣∠ACB＝180°﹣60°＝120°，∴∠ABM＝∠ACD，在△ABM和△ACD中，∵AB ACABM ACDBM CD，∴△ABM≌△ACD（SAS），∴AM＝AD，∠BAM＝∠CAD，∴∠MAD＝∠MAC+∠CAD＝∠MAC+∠BAM＝∠BAC＝60°，∴△AMD是等边三角形，∴AD＝DM＝2DF；【点睛】本题考查了倍长中线的辅助线作法，全等三角形的证明，在倍长中线构造全等三角形的基础上，综合运用相关知识是解题的关键．模型2.截长补短模型【模型解读】截长补短的方法适用于求证线段的和差倍分关系。

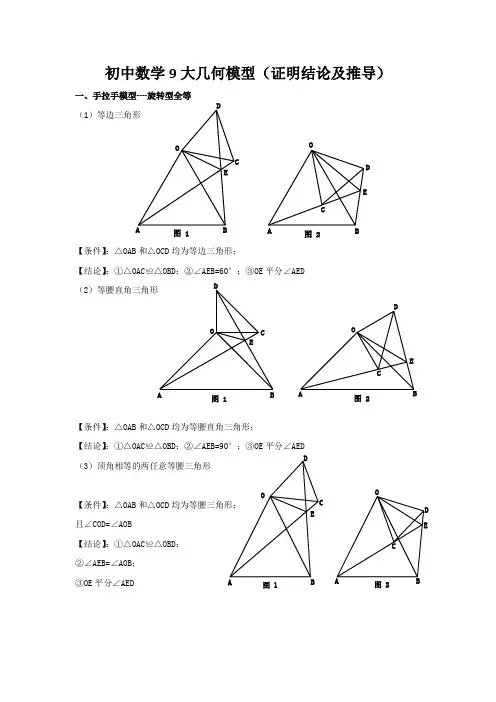
初中数学9大几何模型（证明结论及推导）一、手拉手模型----旋转型全等（1）等边三角形【条件】：△OAB 和△OCD 均为等边三角形；【结论】：①△OAC ≌△OBD ；②∠AEB=60°；③OE 平分∠AED （2）等腰直角三角形【条件】：△OAB 和△OCD 均为等腰直角三角形；【结论】：①△OAC ≌△OBD ；②∠AEB=90°；③OE 平分∠AED （3）顶角相等的两任意等腰三角形【条件】：△OAB 和△OCD 均为等腰三角形； 且∠COD=∠AOB【结论】：①△OAC ≌△OBD ； ②∠AEB=∠AOB ； ③OE 平分∠AEDOABC DE图 1OABC D E图 2OABCDE图 1OACDE图 2OABC DEOABCD E图 1图 2二、模型二：手拉手模型----旋转型相似 （1）一般情况【条件】：CD ∥AB ， 将△OCD 旋转至右图的位置【结论】：①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ； ②延长AC 交BD 于点E ，必有∠BEC=∠BOA （2）特殊情况【条件】：CD∥AB ，∠AOB=90° 将△OCD 旋转至右图的位置 【结论】：①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ； ②延长AC 交BD 于点E ，必有∠BEC=∠BOA ； ③===OAOBOC OD AC BD tan ∠OCD ；④BD ⊥AC ； ⑤连接AD 、BC ，必有2222CD AB B C AD +=+；⑥BD AC 21S △BCD ⨯=三、模型三、对角互补模型 （1）全等型-90°【条件】：①∠AOB=∠DCE=90°；②OC 平分∠AOB【结论】：①CD=CE ；②OD+OE=2OC ；③2△OCE △OCD △DCE OC 21S S S =+= 证明提示：①作垂直，如图2，证明△CDM ≌△CEN②过点C 作CF ⊥OC ，如图3，证明△ODC ≌△FEC ※当∠DCE 的一边交AO 的延长线于D 时（如图4）： 以上三个结论：①CD=CE ；②OE-OD=2OC ； ③2△OCD △OCE OC 21S S =-OB CDO ABCDEOB CDEOA C DAO BCDE图 1A OBCDE M N 图 2A OBCDEF图 3A O BCDEMN 图 4（2）全等型-120°【条件】：①∠AOB=2∠DCE=120°；②OC 平分∠AOB【结论】：①CD=CE ；②OD+OE=OC ；③2△OCE △OCD △DCE OC 43S S S =+=证明提示：①可参考“全等型-90°”证法一；②如右下图：在OB 上取一点F ，使OF=OC ，证明△OCF 为等边三角形。

手拉手模型时间：2021.03.03 创作：欧阳学要点一：手拉手模型特点：由两个等顶角的等腰三角形所组成，并且顶角的顶点为公共顶点结论：（1）△ABD ≌△AEC （2）∠α+∠BOC=180°（3）OA平分∠BOC变形：例 1.如图在直线ABC的同一侧作两个等边三角形ABD∆与∆，连结AE与CD，证明BCE（1）DBC∆≅ABE∆(2)AE与DC之间的夹角为︒60∠(3)HB平分AHC变式精练1：如图两个等边三角形ABD∆与∆，连结AE与CD，BCE证明（1）DBC≅∆ABE∆60（2）AE与DC之间的夹角为︒∠（3）AE与DC的交点设为H,BH平分AHC变式精练2：如图两个等边三角形ABD ∆与BCE ∆，连结AE 与CD ，证明（1）DBC ABE ∆≅∆(2）AE 与DC之间的夹角为︒60 (3）AE 与DC 的交点设为H ,HB 平分AHC ∠例2：如图，两个正方形ABCD 与DEFG ,连结CE AG ,,二者相交于点H问：（1）CDE ADG ∆≅∆是否成立？（2）AG 是否与CE 相等？（3）AG 与CE 之间的夹角为多少度？（4）HD 是否平分AHE ∠？例3：如图两个等腰直角三角形ADC 与EDG ，连结CE AG ,,二者相交于点H问：（1）CDE ADG ∆≅∆是否成立？（2）AG 是否与CE 相等？（3）AG 与CE 之间的夹角为多少度？（4）HD 是否平分AHE ∠？例4：两个等腰三角形ABD ∆与BCE ∆，其中BD AB =,,EB CB =α=∠=∠CBE ABD ,连结AE 与CD ，问：（1）DBC ABE ∆≅∆是否成立？（2）AE 是否与CD 相等？（3）AE 与CD 之间的夹角为多少度？（4）HB 是否平分AHC ∠？例5：如图，点A. B. C 在同一条直线上，分别以AB 、BC 为边在直线AC 的同侧作等边三角形△ABD 、△BCE.连接AE 、DC ，AE 与DC 所在直线相交于F ，连接FB.判断线段FB 、FE 与FC 之间的数量关系，并证明你的结论。

手拉手模子要点一：手拉手模子特色：由两个等顶角的等腰三角形所构成,并且顶角的极点为公共极点结论：（1）△ABD ≌△AEC （2）∠α+∠BOC=180°（3）OA等分∠BOC变形：ABC的统一侧作两个等边三角形∆,贯穿连接AE与CD,证∆与BCEABD实（1）DBC∆≅ABE∆(2)AE与DC之间的夹角为︒60∠(3)HB等分AHC变式精练1：如图两个等边三角形ABD∆与BCE∆,贯穿连接AE与CD,证实（1）DBC∆ABE∆≅60（2）AE与DC之间的夹角为︒∠（3）AE与DC的交点设为H,BH等分AHC变式精练2：如图两个等边三角形ABD∆,贯穿连接AE与CD,∆与BCE证实（1）DBC∆ABE∆≅(2）AE与DC之间的夹角为︒60∠(3）AE与DC的交点设为H,HB等分AHC例2：如图,两个正方形ABCD 与DEFG ,贯穿连接CE AG ,,二者订交于点H 问：（1）CDE ADG ∆≅∆是否成立？（2）AG 是否与CE 相等？（3）AG 与CE 之间的夹角为若干度？ （4）HD 是否等分AHE ∠？例3：如图两个等腰直角三角形ADC 与EDG ,贯穿连接CE AG ,,二者订交于点H问：（1）CDE ADG ∆≅∆是否成立？ （2）AG 是否与CE 相等？（3）AG 与CE 之间的夹角为若干度？ （4）HD 是否等分AHE ∠？例4：两个等腰三角形ABD ∆与BCE ∆,个中穿连接BD AB =,,EB CB =α=∠=∠CBE ABD ,贯AE 与CD ,问：（1）DBC ABE ∆≅∆是否成立？ （2）AE 是否与CD 相等？（3）AE 与CD 之间的夹角为若干度？ （4）HB 是否等分AHC ∠？例5：如图,点A. B. C 在统一条直线上,分离以AB.BC 为边在直线AC 的同侧作等边三角形△ABD.△BCE.衔接AE.DC,AE 与DC 地点直线订交于F,衔接FB.断定线段FB.FE 与FC 之间的数目关系,并证实你的结论.【练1】如图,三角形ABC 和三角形CDE 都是等边三角形,点A,E,D,同在一条直线上,且角EBD=62°,求角AEB 的度数 倍长与中点有关的线段 倍长中线类☞考点解释：凡是消失中线或相似中线的线段,都可以斟酌倍长中线,倍长中线的目标是可以扭转等长度的线段,从而达到将前提进行转化的目标：将题中已知和未知前提分散在一对三角形中.结构全等三角形.平移线段. 【办法精讲】经常运用帮助线添加办法——倍长中线 △ABC 中 方法1：延伸AD 到E,AD 是BC 边中线 使DE=AD,衔接BE方法2：间接倍长作CF⊥AD 于F,延伸MD 到N,作BE⊥AD 的延伸线于 E使DN=MD,衔接BE衔接CD【例1】 已知：ABC ∆中,AM是中线．求证：1()2AM AB AC <+．【练1】在△ABC 中,59AB AC ==，,则BC 边上的中线AD 的长的取值规模是什EDA么？【练2】如图所示,在ABC ∆的AB 边上取两点E .F ,使AE BF =,衔接CE .CF ,求证：AC BC +>EC FC +．【练3】如图,在等腰三角形ABC 中,AB=AC,D 是AB 上一点,F 是AC 延伸线上的一点,且BD=CF,贯穿连接DF交BC 于E ．求证：DE=EF(倍长中线.截长补短)【例2】 如图,已知在ABC∆中,AD 是BC 边上的中线,E 是AD 上一点,延伸BE 交AC 于F ,AF EF =,求证：AC BE =．【练1】如图,已知在ABC ∆中,AD 是BC 边上的中线,E 是AD 上一点,且BE AC =,延伸BE 交AC 于F ,求证：AF EF =【练2】如图,在△ABC 中,AB>AC,E 为BC 边的中点,AD 为∠BAC 的等分线,过E 作AD 的平行线,交AB 于F,交CA 的延伸线于G.求证：BF=CG.【练3】如图,在ABC ∆中,AD 交BC 于点D ,点E 是BC 中点,EF AD ∥交CA 的延伸线于点F ,交AB 于点G ,若BG CF =,求证：AD 为ABC ∆的角等分线．【练4】如图所示,已知ABC ∆中,AD 等分BAC ∠,E .F 分离在BD .AD 上．DE CD =,EF AC =．求证：EF ∥AB【例3】已知AM 为ABC ∆的中线,AMB ∠,AMC ∠的等分线分离交AB 于E .交AC 于F ．求证：BE CF EF +>．【练1】在Rt ABC ∆中,F 是斜边AB 的中点,D .E 分离在边CA .CB 上,知足90DFE ∠=︒．若3AD =,4BE =,则线段DE 的长度为_________．【练2】如图,△ABC 中,AB=2AC,AD 等分BC 且AD⊥AC,则∠BAC=______. 【练3】在ABC ∆中,点D 为BC 的中点,点M .N 分离为AB .AC 上的点,且MD ND ⊥．（1）若90A ∠=︒,以线段BM .MN .CN 为边可否构成一个三角形？若能,该三角形是锐角三角形.直角三角形或钝角三角形？ （2）假如2222BM CN DM DN +=+,求证()22214AD AB AC =+．【例4】如图,等腰直角ABC ∆与等腰直角BDE ∆,P 为CE 中点,衔接PA .PD .探讨PA .PD 的关系.（证角相等办法） 【练1】如图,两个正方形ABDE 和ACGF ,点P 为BC 的中点,衔接PA 交EF 于点Q .探讨AP 与EF 的数目关系和地位关系.（证角相等办法）【练2】如图,在ABC ∆中,AB CD =,BDA BAD ∠=∠,AE 是BD 边的中线.求证：AE AC 2=【例5】如图所示,在ABC ∆中,AB AC =,延伸AB 到D ,使BD AB =,E 为AB 的中点,衔接CE .CD ,求证2CD EC =．【练1】已知ABC ∆中,AB AC =,BD 为AB 的延伸线,且BD AB =,CE 为ABC ∆的AB 边上的中线．求证：2CD CE =【练2】如图,CB.CD 分离是钝角△AEC 和锐角△ABC 中线,且AC=AB,∠ACB=∠ABC.求证CE=2CD. 【例16】如图,两个正方形ABDE 和ACGF ,点P 为BC 的中点,衔接PA 交EF 于点Q .探讨AP 与EF 的数目关系和地位关系.（倍长中线与手拉手模子分解运用） 【练1】已知：如图,正方形ABCD 和正方形EBGF ,点M 是线段DF 的中点. ⑴试解释线段ME 与MC 数目关系和关系.⑵如图,若将上题中正方形EBGF 绕点B 顺时针扭转α度数（︒<90α）,其他前提不变,上述结论还准确吗？若准确,请你证实;若不准确,请解释来由.★全等之截长补短：人教八年级上册教材中,在全等三角形部分介绍了角的等分线的性质,这一性质在很多问题里都有着普遍的运用.而“截长补短法”又是解决这一类问题的一种特别办法(把长边截成两个短边或把两个短边放到一路;消失角等分线进行翻折;有具体角的度数解释请求角的度数,进而得到角相等,∆全等)【例10】 如图所示,ABC ∆中,0045,90=∠=∠B C ,AD等分BAC ∠交BC 于D.求证：AB=AC+CD.【练1】如图所示,在ABC ∆中,060=∠B ,ABC ∆的角D CBOEDA BDOECBANMDCBADA等分线AD.CE 订交于点O.求证：AE+CD=AC.【练2】已知ABC ∆中, 60=∠A ,BD .CE 分离等分ABC ∠和ACB ∠,BD .CE 交于点O ,试断定BE .CD .BC 的数目关系,并加以证实．【练2】如图,在四边形ABCD 中,AD∥BC,AE 等分∠BAD 交DC 于点E,衔接BE,且AE⊥BE,求证：AB=AD+BC.【练3】已知：如图,在△ABC 中,∠A=90∘,AB=AC,BD 是∠ABC 的等分线.求证：BC=AB+AD.【练4】点M,N 在等边三角形ABC 的AB 边上活动,BD=DC,∠BDC=120°,∠MDN=60°,求证MN=MB+NC ．【例11】已知如图所示,在△ABC 中,AD 是角等分线,且AC=AB+BD,试解释∠B=2∠C（不只是边,倍角也实用）【练1】如图,在△ABC 中,AB ＝AC,BD⊥AC 交AC 于点D ．求证：∠DBC＝21∠BAC．【例12】如图所示,已知21∠=∠,P 为BN 上一点,且BCPD ⊥于D,AB+BC=2BD,求证：0180=∠+∠BCP BAP .【练1】如图,在四边形ABCD 中,BC ＞BA,AD ＝CD,BD 等分ABC ∠,求证： 0180=∠+∠C A 【例13】如图所示,在ABCRt ∆21D MCPNA CEDBCA中,AB=AC,090=∠BAC ,CBD ABD ∠=∠,CE 垂直于BD 的延伸线于 E.求证：BD=2CE. 【练1】已知：如图示,在Rt△ABC中,∠A=90°,∠ABC=2∠C,BD 是∠ABC 的等分线．求证：CD=2AD ．【练2】如图所示,在ABC ∆中,090=∠ABC ,AD 为BAC ∠的等分线,C ∠=300,AD BE ⊥于E 点,求证：AC-AB=2BE. 【练3】正方形ABCD,E 是BC 上一点,AE ⊥EF,交∠DCH 的等分线于点F,求证AE=EF【练4】已知在△ABC 中,AB=AC,D 在AB 上,E 在AC 的延伸线上,DE 交BC 于F,且DF=EF,求证：BD=CE【例14】如图所示,已知AB //CD,BCD ABC ∠∠,的等分线正好交于AD 上一点E,求证：BC=AB+CD.【练1】如图,已知AD∥BC,∠PAB 的等分线与∠CBA 的等分线订交于E,CE 的连线交AP 于D ．求证：AD+BC=AB ．【练2】如图,在正方形ABCD 中,F 是CD 的中点,E 是BC 边上的一点,且AF 等分∠DAE,求证：AE=EC+CD ．【练3】在△ABC 中,AD 是BC 边上的高,∠B=2∠C．求证：CD=AB+BD ．【练4】如图所示,在三角形ABC中,∠ACB=90°,AC=BC,D 为三角形ABC 外一点,且AD ＝PEDCBABD,DE⊥AC 交AC 的延伸线于点E.试寻找ED.AE 和BC 之间有何数目关系 【练5】在四边形ABCD 中,AB∥DC,E 为BC 边的中点,∠BAE=∠EAF,AF 与DC 的延伸线订交于点F.试探讨线段AB 与AF.CF 之间的数目关系,并证实你的结论【例15】如图在△ABC 中,AB ＞AC,∠1＝∠2,P 为AD 上随意率性一点,求证：AB-AC ＞PB-PC A12PB C【练1】已知AM 为ABC ∆的中线,AMB ∠,AMC ∠的等分线分离交AB 于E .交AC 于F ．求证：BE CF EF +>．如图,E 是AOB ∠的等分线上一点,OA EC ⊥,OB ED ⊥,垂足为C.D.求证：（1）OC=OD; （2）DF=CF. 结构等边三角形1.如图,已知△ABC 中,AB=AC,D 是CB 延伸线上一点,∠ADB=60∘,E 是AD 上一点,且有DE=DB.求证：AE=BE+BC.2.在等腰ABC ∆中,AB AC =,顶角20A ∠=︒,在边AB 上取点D ,使AD BC =,求BDC ∠. 演习1.如图,在△ABC 中,∠ACB=90°,BE 等分∠ABC,DE⊥AB 于D,假如AC=3cm,那么AE+DE 等于OA.2cmB.3cmC.4cmD.5cm演习2.在△ABC 和△A'B'C'中,AB=A'B',AC=A'C',点D,D'分离是BC,B'C'的中点,且AD=A'D',证眀：'''C B A ABC ∆≅∆.（倍长中线）演习 3.如图,在△ABC 中,BE 是∠ABC 的角等分线,AD⊥BE,垂足为D,求证：∠2=∠1+∠C演习4.如图（1）,已知△ABC 中,∠BAC=90°,AB=AC,AE 是过A 的一条直线,且B.C 在A.E 的异侧,BD⊥AE 于D,CE⊥AE 于E （1）试解释：BD=DE+CE ．（2）若直线AE 绕A 点扭转到图（2）地位时（BD ＜CE ）,其余前提不变,问BD 与DE.CE 的关系若何？请直接写出成果;（3）若直线AE 绕A 点扭转到图（3）地位时（BD ＞CE ）,其余前提不变,问BD 与DE.CE 的关系若何？请直接写出成果,不需解释来由．如图所示,在Rt△ABC 中,AB ＝AC,∠BAC ＝90°,有过A 的任一条直线AN,BD⊥AN 于D,CE⊥AN 于E,求证：DE ＝BD －CE ．（思绪：截长补短法） 如图,在△ABC 中,AB=AC,D 是三角形外一点,且∠ABD=60∘,BD+DC=AB.求证：∠ACD=60∘.（截长补短）1.如图,等腰直角ABC ∆与等腰直角BDE ∆,P 为CE 中点,衔接PA .PD .探讨PA .PD 的关系.（帮助线的连法都一样） 2.已知：如图,正方形ABCD 和正方形EBGF ,点M 是线段DF 的中点.AB C DA 'B 'C 'D '⑴试解释线段ME与MC数目关系和关系.（帮助线的连法都一样）⑵如图,若将上题中正方形EBGF绕点B顺时针扭转α度数（︒α）,其他前提不变,上述结论还准确吗？若准确,请你<90证实;若不准确,请解释来由.3.已知AM为ABC∠的等分线分离交AB于E.交AC于F．∆的中线,AMB∠,AMC求证：BE CF EF+>．（帮助线的连法都一样）【浏览懂得】已知：如图1,等腰直角三角形ABC中,∠B=90°,AD是角等分线,交BC边于点D．求证：AC=AB+BD证实：如图1,在AC上截取AE=AB,衔接DE,则由已知前提易知：Rt△ADB≌Rt△ADE（AAS）∴∠AED=∠B=90°,DE=DB又∵∠C=45°,∴△DEC是等腰直角三角形．∴DE=EC．∴AC=AE+EC=AB+BD．【解决问题】已知,如图2,等腰直角三角形ABC中,∠B=90°,AD是∠BAC的等分线,交BC 边于点D,DE⊥AC,垂足为E,若AB=2,则三角形DEC的周长为．【数学思虑】：现将原题中的“AD是内角等分线,交BC边于点D”换成“AD 是外角等分线,交BC边的延伸线于点D如图3”,其他前提不变,请你猜测线段AC.AB.BD之间的数目关系,并证实你的猜测．【类比猜测】随意率性三角形ABC,∠ABC=2∠C,AD是∠BAC的外角等分线,交CB边的延伸线于点D,如图4,请你写出线段AC.AB.BD之间的数目关系．如图,已知∠B=∠C=90°,M是BC的中点,DM等分∠ADC.（1）求证：AM等分∠DAB（2）试解释线段DM与AM有如何的地位关系？（3）线段CD.AB.AD间有如何的关系？直接写出成果.。

初二下册数学几何模型归纳在初二下册的数学学习中，几何部分的知识变得更加丰富和复杂。

为了更好地理解和解决几何问题，掌握一些常见的几何模型是非常重要的。

下面就为大家归纳一下初二下册数学中常见的几何模型。

一、全等三角形模型1、手拉手模型两个顶角相等且有公共顶点的等腰三角形所组成的图形。

例如，在三角形 ABC 和三角形 ADE 中，AB ＝ AC，AD ＝ AE，且∠BAC ＝∠DAE，通过证明全等可以得到一些线段和角的关系。

2、倍长中线模型遇到中线时，可以将中线延长一倍，构造全等三角形。

例如，在三角形 ABC 中，AD 是中线，延长 AD 至 E，使 DE ＝ AD，连接 BE，可证明三角形 ADC 和三角形 EDB 全等。

3、一线三等角模型一条直线上有三个相等的角，通常可以通过相似或全等三角形来解决问题。

二、相似三角形模型1、 A 字模型形如“A”字的相似三角形，通常是由平行线得到的。

2、 8 字模型形如“8”字的相似三角形，通过对顶角和同位角等证明相似。

3、射影定理模型在直角三角形中，斜边上的高把斜边分成两段，这两段的乘积等于高的平方。

三、等腰三角形模型1、等腰三角形三线合一等腰三角形底边上的高线、中线、顶角平分线互相重合。

2、等腰三角形的性质和判定要熟练掌握等腰三角形两腰相等、两底角相等，以及通过等角对等边或等边对等角来判定等腰三角形。

四、直角三角形模型1、勾股定理直角三角形两直角边的平方和等于斜边的平方。

2、直角三角形斜边上的中线等于斜边的一半。

3、特殊的直角三角形比如含 30°角的直角三角形，三边的比例关系为 1 ：√3 ： 2；含 45°角的直角三角形，三边比例关系为 1 ： 1 ：√2 。

五、平行四边形模型1、平行四边形的性质对边平行且相等，对角相等，对角线互相平分。

2、平行四边形的判定从对边、对角、对角线等方面进行判定。

六、矩形模型矩形具有平行四边形的所有性质，并且四个角都是直角，对角线相等。

专题01全等模型-倍长中线与截长补短全等三角形在中考数学几何模块中占据着重要地位，也是学生必须掌握的一块内容，本专题就全等三角形中的重要模型（倍长中线模型、截长补短模型）进行梳理及对应试题分析，方便掌握。

模型1.倍长中线模型【模型解读】中线是三角形中的重要线段之一，在利用中线解决几何问题时，常常采用“倍长中线法”添加辅助线．所谓倍长中线法，就是将三角形的中线延长一倍，以便构造出全等三角形，从而运用全等三角形的有关知识来解决问题的方法．（注：一般都是原题已经有中线时用，不太会有自己画中线的时候）。

【常见模型及证法】1、基本型：如图1，在三角形ABC 中，AD 为BC 边上的中线.证明思路：延长AD 至点E ，使得AD =DE .若连结BE ，则BDE CDA ∆≅∆；若连结EC ，则ABD ECD ∆≅∆；2、中点型:如图2，C 为AB 的中点.证明思路：若延长EC 至点F ，使得CF EC =，连结AF ，则BCE ACF ∆≅∆;若延长DC 至点G ，使得CG DC =，连结BG ，则ACD BCG ∆≅∆.3、中点+平行线型：如图3,//AB CD ，点E 为线段AD 的中点.证明思路：延长CE 交AB 于点F (或交BA 延长线于点F )，则EDC EAF ∆≅∆.例1．（2023·成都市·八年级课时练习）【阅读理解】课外兴趣小组活动时，老师提出了如下问题：如图，△ABC 中，若AB ＝8，AC ＝6，求BC 边上的中线AD 的取值范围．小明在组内经过合作交流，得到了如下的解决方法：如图，延长AD 到点E ，使DE ＝AD ，连结BE ．请根据小明的方法思考：(1)由已知和作图能得到ADC EDB ≌△△的理由是（）．A ．SSS B ．SAS C ．AASD ．ASA (2)AD 的取值范围是（）．A ．68AD <<B ．1216AD <<C ．17AD <<D ．214AD <<(3)【感悟】解题时，条件中若出现“中点”、“中线”字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论转化到同一个三角形中．【问题解决】如图，AD 是△ABC 的中线，BE 交AC 于点E ，交AD 于F ，且AE ＝EF ．求证：AC ＝BF．【答案】(1)B (2)C (3)见解析【分析】（1）根据AD =DE ，∠ADC =∠BDE ，BD =DC 推出△ADC 和△EDB 全等即可；（2）根据全等得出BE =AC =6，AE =2AD ，由三角形三边关系定理得出8-6＜2AD ＜8+6，求出即可；（3）延长AD 到M ，使AD =DM ，连接BM ，根据SAS 证△ADC ≌△MDB ，推出BM =AC ，∠CAD =∠M ，根据AE =EF ，推出∠CAD =∠AFE =∠BFD ，求出∠BFD =∠M ，根据等腰三角形的性质求出即可．（1）∵在△ADC 和△EDB 中AD DE ADC BDE BD CD ⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ADC ≌△EDB （SAS ），故选B ；（2）∵由（1）知：△ADC ≌△EDB ，∴BE =AC =6，AE =2AD ，∵在△ABE 中，AB =8，由三角形三边关系定理得：8-6＜2AD ＜8+6，∴1＜AD ＜7，故选：C ．（3）延长AD 到点M ，使AD ＝DM ，连接BM ．∵AD 是△ABC 中线∴CD ＝BD∵在△ADC 和△MDB 中DC DB ADC MDB DA DM =⎧⎪∠=∠⎨⎪=⎩∴()SAS ADC MDB ≌△△∴BM ＝AC （全等三角形的对应边相等）∠CAD ＝∠M （全等三角形的对应角相等）∵AE ＝EF ，∴∠CAD ＝∠AFE （等边对等角）∵∠AFE ＝∠BFD ，∴∠BFD ＝∠M ，∴BF ＝BM （等角对等边）又∵BM ＝AC ，∴AC ＝BF ．【点睛】本题考查了三角形的中线，三角形的三边关系定理，等腰三角形性质和判定，全等三角形的性质和判定等知识点，主要考查学生运用定理进行推理的能力．例2．（2022·河南南阳·中考模拟）【教材呈现】如图是华师版八年级上册数学教材第69页的部分内容：如图，在ABC 中，D 是边BC 的中点，过点C 画直线CE ，使//CE AB ，交AD 的延长线于点E ，求证：AD ED =证明∵//CE AB （已知）∴ABD ECD ∠=∠，BAD CED ∠=∠（两直线平行，内错角相等）．在ABD △与ECD 中，∵ABD ECD ∠=∠，BAD CED ∠=∠（已证），BD CD =（已知），∴()A.A.S ABD ECD △△≌，∴AD ED =（全等三角形的对应边相等）．（1）【方法应用】如图①，在ABC 中，6AB =，4AC =，则BC 边上的中线AD 长度的取值范围是______．（2）【猜想证明】如图②，在四边形ABCD 中，//AB CD ，点E 是BC 的中点，若AE 是BAD ∠的平分线，试猜想线段AB 、AD 、DC 之间的数量关系，并证明你的猜想；（3）【拓展延伸】如图③，已知//AB CF ，点E 是BC 的中点，点D 在线段AE 上，EDF BAE ∠=∠，若5AB =，2CF =，求出线段DF 的长．【答案】（1）1＜AD ＜5；（2）AD =AB +DC ．理由见解析；（3）DF =3．【分析】（1）延长AD 到E ，使AD =DE ，连接BE ，证△ADC ≌△EDB ，推出AC =BE =4，在△ABE 中，根据三角形三边关系定理得出AB -BE ＜AE ＜AB +BE ，代入求出即可；（2）结论：AD =AB +DC ．延长AE ，DC 交于点F ，证明△ABE ≌△FEC （AAS ），推出AB =CF ，再证明DA =DF 即可解决问题；（3）如图③，延长AE 交CF 的延长线于点G ，证明AB =DF +CF ，可得结论．【详解】解：（1）延长AD 到E ，使AD =DE ，连接BE ，∵AD 是BC 边上的中线，∴BD =CD ，在△ADC和△EDB中，AD DEADC EDBDC DB=⎧⎪∠=∠⎨⎪=⎩，∴△ADC≌△EDB（SAS），∴AC=BE=4，在△ABE中，AB-BE＜AE＜AB+BE，∴6-4＜2AD＜6+4，∴1＜AD＜5，故答案为：1＜AD＜5；（2）结论：AD=AB+DC．理由：如图②中，延长AE，DC交于点F，∵AB∥CD，∴∠BAF=∠F，在△ABE和△FCE中，AEB FECBAE FBE CE∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ABE≌△FCE（AAS），∴CF=AB，∵AE是∠BAD的平分线，∴∠BAF=∠FAD，∴∠FAD=∠F，∴AD=DF，∵DC+CF=DF，∴DC+AB=AD；（3）如图③，延长AE交CF的延长线于点G，∵E是BC的中点，∴CE=BE，∵AB∥CF，∴∠BAE=∠G，在△AEB和△GEC中，BAE GAEB GECBE CE∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△AEB≌△GEC（AAS），∴AB=GC，∵∠EDF=∠BAE，∴∠FDG=∠G，∴FD=FG，∴AB=DF+CF，∵AB=5，CF=2，∴DF=AB-CF=3．【点睛】本题考查了全等三角形的判定与性质、等腰三角形的判定与性质、角平分线的性质、三角形三边关系等知识点，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．例3．（2022·贵州毕节·二模）课外兴趣小组活动时，老师提出了如下问题：(1)如图1，△ABC中，若AB=5，AC=3，求BC边上的中线AD的取值范围．小明在组内经过合作交流，得到了如下的解决方法：延长AD到点E，使DE=AD，请根据小明的方法思考帮小明完成解答过程．(2)如图2，AD是△ABC的中线，BE交AC干E，交AD于F，且AE=EF．请判昕AC与BF的数量关系，并说明理由．【答案】(1)见解析(2)AC=BF，理由见解析【解析】（1）解：如图，延长AD到点E，使DE=AD，连接BE，在△ADC和△EDB中∵AD DEADC EDBCD DB=⎧⎪∠=∠⎨⎪=⎩，∴△ADC≌△EDB（SAS）．∴BE=AC=3．∵AB-BE<AE<AB+BE∵2<AE<8．∵AE=2AD∴1<AD<4．（2）AC=BF，理由如下：延长AD至点G，使GD=AD，连接BG，在△ADC和△GDB中，AD DGADC GDBBD CD=⎧⎪∠=∠⎨⎪=⎩，∴△ADC≌△GDB（SAS）．∴BG=AC，∠G=∠DAC．．∵AE=EF∴∠AFE=∠FAE．∴∠DAC=∠AFE=∠BFG∴∠G=∠BFG∴BG=BF∴AC=BF．【点睛】本题考查全等三角形判定与性质，三角形三边的关系，作辅助线：延长AD到点E，使DE=AD，构造全等三角形是解题的关键．例4．（2022·山东·安丘市一模）阅读材料：如图1，在ABC中，D，E分别是边AB，AC的中点，小亮在证明“三角形的中位线平行于第三边，且等于第三边的一半”时，通过延长DE到点F，使EF DE=，连接CF ，证明ADE CFE ≌，再证四边形DBCF是平行四边形即得证．类比迁移：（1）如图2，AD 是ABC 的中线，E 是AC 上的一点，BE 交AD 于点F ，且AE EF =，求证：AC BF =．小亮发现可以类比材料中的思路进行证明．证明：如图2，延长AD 至点M ，使MD FD =，连接MC ，……请根据小亮的思路完成证明过程．方法运用：（2）如图3，在等边ABC 中，D 是射线BC 上一动点（点D 在点C 的右侧），连接AD ．把线段CD 绕点D 逆时针旋转120°得到线段DE ，F 是线段BE 的中点，连接DF 、CF ．请你判断线段DF 与AD 的数量关系，并给出证明．【答案】（1）证明见解析；（2）2AD DF =，证明见解析【分析】(1)延长AD 至M ，使MD FD =，连接MC ，证明BDF CDM △≌△，结合等角对等边证明即可．(2)延长DF 至点M ，使DF FM =，连接BM 、AM ，证明(SAS)ABM ACD △≌△，△ABM 是等边三角形，代换后得证．【详解】（1）证明：延长AD 至M ，使MD FD =，连接MC ．在BDF 和CDM V 中，BD CD BDF CDM DF DM =⎧⎪∠=∠⎨⎪=⎩，∴BDF CDM △≌△，∴MC BF =，M BFM ∠=∠，∵AE EF =，∴EAF EFA ∠=∠，∵EFA BFM ∠=∠，∴M MAC ∠=∠，∴AC MC =，∴AC BF =．（2）线段DF 与AD 的数量关系为：2AD DF =．证明如下：延长DF 至点M ，使DF FM =，连接BM 、AM ，如图2所示：∵点F 为BE 的中点，∴BF EF=在BFM 和EFD △中，∵BF EF BFM EFD FM DF =⎧⎪∠=∠⎨⎪=⎩，∴(SAS)BFM EFD △≌△∴BM DE =，MBF DEF ∠=∠，∴BM DE∥∵线段CD 绕点D 逆时针旋转120°得到线段DE∴CD DE BM ==，120∠=︒BDE ，∴18012060MBD ∠=-=︒︒︒∵ABC 是等边三角形∵AB AC =，60ABC ACB ∠=∠=︒，∴6060120ABM ABC MBD ∠∠∠︒︒=+=+=︒∵180********ACD ACB ∠=︒-∠=︒-︒=︒，∴ABM ACD∠=∠在ABM 和ACD △中，∵AB AC ABM ACD BM CD =⎧⎪∠=∠⎨⎪=⎩，∴(SAS)ABM ACD △≌△∴AM AD =，BAM CAD ∠=∠，∴60MAD MAC CAD MAC BAM BAC ∠∠∠∠∠∠=+=+==︒∴AMD 是等边三角形，∴2==AD DM DF ．【点睛】本题考查了等边三角形的判定和性质，三角形全等的判定和性质，熟练掌握等边三角形的判定和性质，三角形全等的判定和性质是解题的关键．模型2.截长补短模型【模型解读】截长补短的方法适用于求证线段的和差倍分关系。

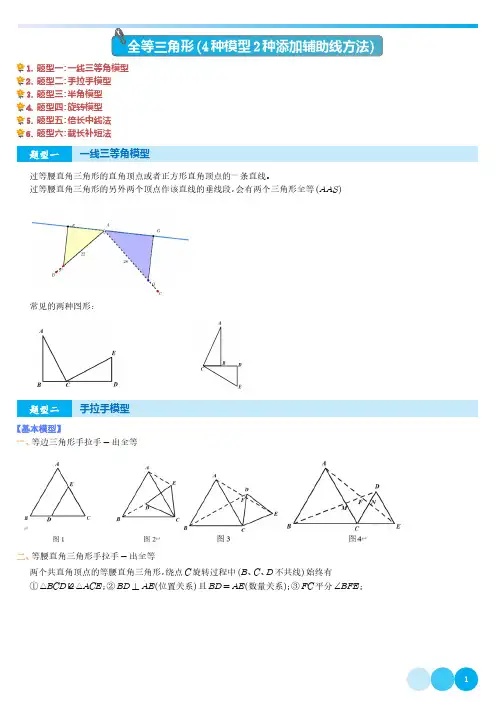
全等三角形(4种模型2种添加辅助线方法)1.题型一：一线三等角模型2.题型二：手拉手模型3.题型三：半角模型4.题型四：旋转模型5.题型五：倍长中线法6.题型六：截长补短法题型一一线三等角模型过等腰直角三角形的直角顶点或者正方形直角顶点的一条直线。

过等腰直角三角形的另外两个顶点作该直线的垂线段，会有两个三角形全等(AAS)常见的两种图形：题型二手拉手模型【基本模型】一、等边三角形手拉手-出全等二、等腰直角三角形手拉手-出全等两个共直角顶点的等腰直角三角形，绕点C旋转过程中(B、C、D不共线)始终有①△BCD≌△ACE；②BD⊥AE(位置关系)且BD=AE(数量关系)；③FC平分∠BFE；12题型三半角模型过等腰三角形顶点两条射线，使两条射线的夹角为等腰三角形顶角的一半这样的模型称为半角模型。

常见的图形为正方形，正三角形，等腰直角三角形等，解题思路一般是将半角两边的三角形通过旋转到一边合并成新的三角形，从而进行等量代换，然后证明与半角形成的三角形全等，再通过全等的性质得到线段之间的数量关系。

解题技巧：在图1中，△AEB 由△AND 旋转所得，可得△AEM ≌△AMN ，∴BM +DN =MN∠AMB =∠AMNAB =AH△CMN 的周长等于正方形周长的一半在图2中将△ABC 旋转至△BEF ，易得△BED ≌△BCD 同理得到边角之间的关系；总之：半角模型(题中出现角度之间的半角关系)利用旋转--证全等--得到相关结论.题型四旋转模型31一、奔驰模型旋转是中考必考题型，奔驰模型是非常经典的一类题型，且近几年中考中经常出现。

我们不仅要掌握这类题型，提升利用旋转解决问题的能力，更重要的是要明白一点:旋转的本质是把分散的条件集中化，从而解决问题2二、费马点模型费马点就是到三角形的三个顶点距离之和最小的点.最值问题是中考常考题型，费马点属于几何中的经典题型，目前全国范围内的中考题都是从经典题改编而来，所以掌握费马点等此类最值经典题是必不可少的.题型五倍长中线法三角形一边的中线(与中点有关的线段)，或中点，通常考虑倍长中线或类中线，构造全等三角形.把该中线延长一倍，证明三角形全等，从而运用全等三角形的有关知识来解决问题的方法.主要思路：倍长中线(线段)造全等4在△ABC 中AD 是BC边中线延长AD 到E ，使DE =AD ，连接BE作CF ⊥AD 于F ，作BE ⊥AD 的延长线于E 连接BE延长MD 到N ，使DN =MD ，连接CD截长补短法截长补短法在初中几何教学中有着十分重要的作用,它主要是用来证线段的和差问题,而且这种方法一直贯穿着整个几何教学的始终.那么什么是截长补短法呢?所谓截长补短其实包含两层意思,即截长和补短.截长就是在较长的线段上截取一段等于要证的两段较短的线段中的一段,证剩下的那一段等于另外一段较短的线段.当条件或结论中出现a +b =c 时，用截长补短．1.补短法：通过添加辅助线“构造”一条线段使其为求证中的两条线段之和，在证所构造的线段和求证中那一条线段相等；2.截长法：通过添加辅助线先在求证中长线段上截取与线段中的某一段相等的线段，在证明截剩部分与线段中的另一段相等。

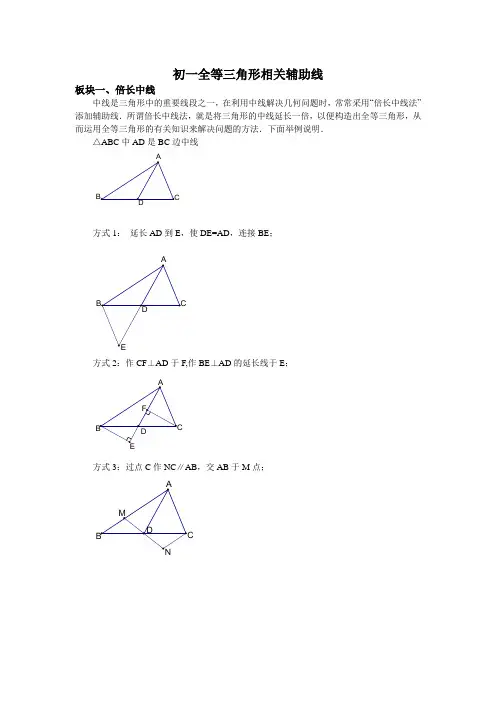
初一全等三角形相关辅助线板块一、倍长中线中线是三角形中的重要线段之一，在利用中线解决几何问题时，常常采用“倍长中线法”添加辅助线．所谓倍长中线法，就是将三角形的中线延长一倍，以便构造出全等三角形，从而运用全等三角形的有关知识来解决问题的方法．下面举例说明．△ABC中AD是BC边中线方式1：延长AD到E，使DE=AD，连接BE；方式2：作CF⊥AD于F,作BE⊥AD的延长线于E；方式3：过点C作NC∥AB，交AB于M点；例1 如图，在△ABC 中，AD 为BC 边上的中线．求证：AB +AC ＞2AD ．DABC例2 如图，在△ABC 中，AB ＞AC ，E 为BC 边的中点，AD 为∠BAC的平分线，过E 作AD 的平行线，交AB 于F ，交CA 的延长线于G ．求证：BF =CG ．例3 如图4，CB ，CD 分别是钝角△AEC 和锐角△ABC 的中线，且AC =AB ．求证：CE =2CD ．变式1：已知在△ABC 中，AD 是BC 边上的中线，E 是AD 上一点，且BE=AC ，延长BE 交AC 于F ，求证：AF=EF变式2：在四边形ABCD 中，AB ∥DC ，E 为BC 边的中点，∠BAE=∠EAF ，AF 与DC 的延长线相交于点F ，求证：AB=AF+CF 。

FEDBCEABC课堂练习：如图， 在ABC ∆中，AC AB ≠，D 、E 在BC 上，且DE=EC ，过D 作BA DF //交AE 于点F ，DF=AC. 求证：AE 平分BAC ∠第 1 题图ABFDEC板块二、角平分线角平分线是三角形中的重要线段之一，在利用角平分线解决几何问题时，常常采用“轴对称”添加辅助线．所谓轴对称，根据翻折对称的思想，构造出全等三角形，从而运用全等三角形的有关知识来解决问题的方法．下面举例说明．(l)若PA ⊥OM 于点A ，如图 (a)，可以过P 点作PB ⊥ON 于点B ，则PB=PA.可记为“图中有角平分线，可向两边作垂线”．(a)B AOPM N(b)B OPMNA(2)若点A 是射线OM 上任意一点，如图 (b)，可以在ON 上截取OB=OA ，连接PB ，构造△OPB ∽△OPA.可记为“图中有角平分线，可以将图对折看，对称以后关系现”．(3)若AP ⊥OP 于点P ，如图 (c)，可以延长AP 交ON 于点B ，构造△AOB 是等腰三角形，P 是底边AB 的中点，可记为“角平分线加垂线，三线合一试试看”．(c)BAOPM N(d)QOPMN(4)若过P 点作PQ ∥ON 交OM 于点Q ，如图 (d)，可以构造△POQ 是等腰三角形，可记为“角平分线十平行线，等腰三角形必呈现”．例1 (1)如图2-3(a)，在△ABC 中，∠C=90。

手拉手模型欧阳引擎（2021.01.01）要点一：手拉手模型特点：由两个等顶角的等腰三角形所组成，并且顶角的顶点为公共顶点结论：（1）△ABD ≌△AEC （2）∠α+∠BOC=180°（3）OA平分∠BOC变形：例 1.如图在直线ABC的同一侧作两个等边三角形ABD∆与∆，连结AE与CD，证明BCE（1）DBC∆ABE∆≅(2)AE与DC之间的夹角为︒60∠(3)BH平分AHC变式精练1：如图两个等边三角形ABD∆与BCE∆，连结AE与CD，证明（1）DBC∆≅ABE∆60（2）AE与DC之间的夹角为︒∠（3）AE与DC的交点设为H,BH平分AHC变式精练2：如图两个等边三角形ABD∆，连结AE与∆与BCECD ，证明（1）DBC ABE ∆≅∆(2）AE 与DC之间的夹角为︒60 (3）AE 与DC 的交点设为H ,BH 平分AHC ∠例2：如图，两个正方形ABCD 与DEFG ,连结CE AG ,,二者相交于点H问：（1）CDE ADG ∆≅∆是否成立？（2）AG 是否与CE 相等？（3）AG 与CE 之间的夹角为多少度？（4）HD 是否平分AHE ∠？例3：如图两个等腰直角三角形ADC 与EDG ，连结CE AG ,,二者相交于点H问：（1）CDE ADG ∆≅∆是否成立？（2）AG 是否与CE 相等？（3）AG 与CE 之间的夹角为多少度？（4）HD 是否平分AHE ∠？例4：两个等腰三角形ABD ∆与BCE ∆，其中BD AB =,,EB CB =α=∠=∠CBE ABD ,连结AE 与CD ，问：（1）DBC ABE ∆≅∆是否成立？（2）AE 是否与CD 相等？（3）AE 与CD 之间的夹角为多少度？（4）HB 是否平分AHC ？例5：如图，点A. B. C 在同一条直线上，分别以AB 、BC 为边在直线AC 的同侧作等边三角形△ABD 、△BCE.连接AE 、DC ，AE 与DC 所在直线相交于F ，连接FB.判断线段FB 、FE 与FC 之间的数量关系，并证明你的结论。

全等三角形八大基本模型摘要：1.全等三角形的定义与性质2.全等三角形的八大基本模型1.手拉手模型2.一线三垂直模型3.一线三等角模型4.等腰三角形中边边角模型5.背对背模型6.半角旋转模型7.角分线模型8.正方形手拉手模型正文：全等三角形是指两个三角形的对应边和对应角分别相等的三角形。

在解决全等三角形问题时，我们需要了解全等三角形的定义和性质，同时掌握一些常用的模型。

本文将介绍全等三角形的八大基本模型，希望能帮助大家更好地理解和解决全等三角形问题。

1.手拉手模型：两个三角形通过一个公共边，并且这个公共边的两个相邻角分别相等。

2.一线三垂直模型：两个三角形有一个公共边，并且这个公共边的两个相邻角分别相等，同时还有另一条公共边上的一个角与另一个角的补角相等。

3.一线三等角模型：两个三角形有一个公共边，并且这个公共边上的三个角分别相等。

4.等腰三角形中边边角模型：两个等腰三角形，其中一个等腰三角形的底边与另一个等腰三角形的腰相等，同时这两个等腰三角形的底角分别相等。

5.背对背模型：两个三角形分别有一个角和另一个角的补角相等，且这两个三角形的另一条边分别相等。

6.半角旋转模型：两个三角形有一个公共边，并且这个公共边的两个相邻角中有一个角是另一个角的一半。

7.角分线模型：两个三角形有一个公共边，并且这个公共边上的一个角平分另一个角。

8.正方形手拉手模型：两个正方形，其中一个正方形的边与另一个正方形的对角线相等。

在解决全等三角形问题时，我们可以根据题目所给的条件，结合全等三角形的性质和八大基本模型，通过适当的变换和推理，证明两个三角形全等。