最优装载问题
- 格式:ppt
- 大小:132.50 KB
- 文档页数:14
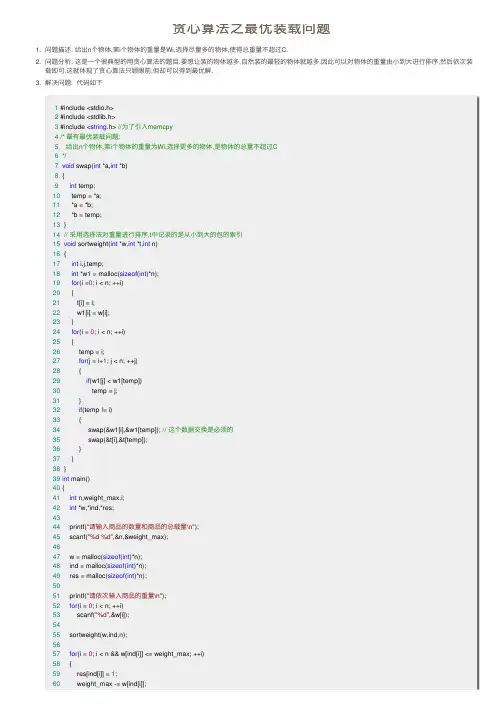
贪⼼算法之最优装载问题1. 问题描述: 给出n个物体,第i个物体的重量是Wi,选择尽量多的物体,使得总重量不超过C.2. 问题分析: 这是⼀个很典型的⽤贪⼼算法的题⽬.要想让装的物体越多,⾃然装的最轻的物体就越多.因此可以对物体的重量由⼩到⼤进⾏排序,然后依次装载即可.这就体现了贪⼼算法只顾眼前,但却可以得到最优解.3. 解决问题: 代码如下4. 1 #include <stdio.h>2 #include <stdlib.h>3 #include <string.h> //为了引⼊memcpy4/* 最有最优装载问题:5给出n个物体,第i个物体的重量为Wi,选择更多的物体,是物体的总量不超过C6*/7void swap(int *a,int *b)8 {9int temp;10 temp = *a;11 *a = *b;12 *b = temp;13 }14// 采⽤选择法对重量进⾏排序,t中记录的是从⼩到⼤的包的索引15void sortweight(int *w,int *t,int n)16 {17int i,j,temp;18int *w1 = malloc(sizeof(int)*n);19for(i =0; i < n; ++i)20 {21 t[i] = i;22 w1[i] = w[i];23 }24for(i = 0; i < n; ++i)25 {26 temp = i;27for(j = i+1; j < n; ++j)28 {29if(w1[j] < w1[temp])30 temp = j;31 }32if(temp != i)33 {34 swap(&w1[i],&w1[temp]); // 这个数据交换是必须的35 swap(&t[i],&t[temp]);36 }37 }38 }39int main()40 {41int n,weight_max,i;42int *w,*ind,*res;4344 printf("请输⼊商品的数量和商品的总载量\n");45 scanf("%d %d",&n,&weight_max);4647 w = malloc(sizeof(int)*n);48 ind = malloc(sizeof(int)*n);49 res = malloc(sizeof(int)*n);5051 printf("请依次输⼊商品的重量\n");52for(i = 0; i < n; ++i)53 scanf("%d",&w[i]);5455 sortweight(w,ind,n);5657for(i = 0; i < n && w[ind[i]] <= weight_max; ++i)58 {59 res[ind[i]] = 1;60 weight_max -= w[ind[i]];61 }62 printf("贪⼼算法求解后的结果是:\n");63for(i = 0; i < n; ++i)64 {65 printf("%d ",res[i]);66 }67 printf("\n");68return0;69 }4. 程序分析: 由于不要改变原始物体重量的值,所以在排序的时候要另外再开辟⼀个数组存储重量.并且另外开辟ind[]存放索引记录装载的顺序.ind[]存放的是重量数组中每个元素在这组数组中⼤⼩的顺序(索引).怎样在排序时记录索引需要在练习排序的时候注意下.。

.. . .. . ..算法分析与设计2016/2017(2)实验题目装载问题5种解法学生姓名学生学号. 专业学习资料... . .. . ..学生班级任课教师提交日期2017计算机科学与技术学目录一问题定义 (4)二解决方案 (4)1优先队列式分支限界法求解 (4)1.1算法分析 (4)1.2代码 (4)1.3运行结果 (17)2队列式分支限界法求解 (17)2.1算法分析 (17)2.2代码 (18)2.3测试截图 (30)3回朔法-迭代 (30)3.1算法分析 (30)3.2代码 (30)3.3测试截图 (35)4回朔法-递归 (35)4.1算法分析 (35)4.2代码 (35). 专业学习资料... . .. . ..4.3测试截图 (41)5贪心算法 (42)5.1算法分析 (42)5.2代码 (42)5.3测试截图 (46). 专业学习资料.一问题定义有一批共有n 个集装箱要装上两艘载重量分别为c1 和c2 的轮船,其中集装箱i 的重量为w[i], 且重量之和小于(c1 + c2)。
装载问题要求确定是否存在一个合理的装载方案可将这n 个集装箱装上这两艘轮船。
如果有,找出一种装载方案。
二解决方案1优先队列式分支限界法求解1.1算法分析活结点x在优先队列中的优先级定义为从根结点到结点x的路径所相应的载重量再加上剩余集装箱的重量之和。
优先队列中优先级最大的活结点成为下一个扩展结点。
以结点x为根的子树中所有结点相应的路径的载重量不超过它的优先级。
子集树中叶结点所相应的载重量与其优先级相同。
在优先队列式分支限界法中,一旦有一个叶结点成为当前扩展结点,则可以断言该叶结点所相应的解即为最优解。
此时可终止算法。
1.2代码1.2-1////MaxHeap.htemplate<class T>class MaxHeap{public:MaxHeap(int MaxHeapSize = 10);~MaxHeap() {delete [] heap;}int Size() const {return CurrentSize;}T Max(){ //查找if (CurrentSize == 0){throw OutOfBounds();}return heap[1];}MaxHeap<T>& Insert(const T& x); //增MaxHeap<T>& DeleteMax(T& x); //删void Initialize(T a[], int size, int ArraySize);private:int CurrentSize, MaxSize;T *heap; // element array};template<class T>MaxHeap<T>::MaxHeap(int MaxHeapSize){// Max heap constructor.MaxSize = MaxHeapSize;heap = new T[MaxSize+1];CurrentSize = 0;}template<class T>MaxHeap<T>& MaxHeap<T>::Insert(const T& x){// Insert x into the max heap.if (CurrentSize == MaxSize){cout<<"no space!"<<endl;return *this;}// 寻找新元素x的位置// i——初始为新叶节点的位置,逐层向上,寻找最终位置int i = ++CurrentSize;while (i != 1 && x > heap[i/2]){// i不是根节点,且其值大于父节点的值,需要继续调整heap[i] = heap[i/2]; // 父节点下降i /= 2; // 继续向上,搜寻正确位置}heap[i] = x;return *this;}template<class T>MaxHeap<T>& MaxHeap<T>::DeleteMax(T& x){// Set x to max element and delete max element from heap. // check if heap is emptyif (CurrentSize == 0){cout<<"Empty heap!"<<endl;return *this;}x = heap[1]; // 删除最大元素// 重整堆T y = heap[CurrentSize--]; // 取最后一个节点,从根开始重整// find place for y starting at rootint i = 1, // current node of heapci = 2; // child of iwhile (ci <= CurrentSize){// 使ci指向i的两个孩子中较大者if (ci < CurrentSize && heap[ci] < heap[ci+1]){ci++;}// y的值大于等于孩子节点吗?if (y >= heap[ci]){break; // 是,i就是y的正确位置,退出}// 否,需要继续向下,重整堆heap[i] = heap[ci]; // 大于父节点的孩子节点上升i = ci; // 向下一层,继续搜索正确位置ci *= 2;}heap[i] = y;return *this;}template<class T>void MaxHeap<T>::Initialize(T a[], int size,int ArraySize){// Initialize max heap to array a.delete [] heap;heap = a;CurrentSize = size;MaxSize = ArraySize;// 从最后一个内部节点开始,一直到根,对每个子树进行堆重整 for (int i = CurrentSize/2; i >= 1; i--){T y = heap[i]; // 子树根节点元素// find place to put yint c = 2*i; // parent of c is target// location for ywhile (c <= CurrentSize){// heap[c] should be larger siblingif (c < CurrentSize && heap[c] < heap[c+1]) {c++;}// can we put y in heap[c/2]?if (y >= heap[c]){break; // yes}// noheap[c/2] = heap[c]; // move child upc *= 2; // move down a level}heap[c/2] = y;}}1.2-2///6d3-2.cpp//装载问题优先队列式分支限界法求解#include "stdafx.h"#include "MaxHeap.h"#include <iostream>using namespace std;const int N = 4;class bbnode;template<class Type>class HeapNode{template<class Type>friend void AddLiveNode(MaxHeap<HeapNode<Type>>& H,bbnode *E,Type wt,bo ol ch,int lev);template<class Type>friend Type MaxLoading(Type w[],Type c,int n,int bestx[]);public:operator Type() const{return uweight;}private:bbnode *ptr; //指向活节点在子集树中相应节点的指针Type uweight; //活节点优先级(上界)int level; //活节点在子集树中所处的层序号};class bbnode{template<class Type>friend void AddLiveNode(MaxHeap<HeapNode<Type>>& H,bbnode *E,Type wt,bo ol ch,int lev);template<class Type>friend Type MaxLoading(Type w[],Type c,int n,int bestx[]);friend class AdjacencyGraph;private:bbnode *parent; //指向父节点的指针bool LChild; //左儿子节点标识};template<class Type>void AddLiveNode(MaxHeap<HeapNode<Type>>& H,bbnode *E,Type wt,bool ch,int l ev);template<class Type>Type MaxLoading(Type w[],Type c,int n,int bestx[]);int main(){float c = 70;float w[] = {0,20,10,26,15};//下标从1开始int x[N+1];float bestw;cout<<"轮船载重为:"<<c<<endl;cout<<"待装物品的重量分别为:"<<endl;for(int i=1; i<=N; i++){cout<<w[i]<<" ";}cout<<endl;bestw = MaxLoading(w,c,N,x);cout<<"分支限界选择结果为:"<<endl;for(int i=1; i<=4; i++){cout<<x[i]<<" ";}cout<<endl;cout<<"最优装载重量为:"<<bestw<<endl;return 0;}//将活节点加入到表示活节点优先队列的最大堆H中template<class Type>void AddLiveNode(MaxHeap<HeapNode<Type>>& H,bbnode *E,Type wt,bool ch,int l ev){bbnode *b = new bbnode;b->parent = E;b->LChild = ch;HeapNode<Type> N;N.uweight = wt;N.level = lev;N.ptr = b;H.Insert(N);}//优先队列式分支限界法,返回最优载重量,bestx返回最优解template<class Type>Type MaxLoading(Type w[],Type c,int n,int bestx[]){//定义最大的容量为1000MaxHeap<HeapNode<Type>> H(1000);//定义剩余容量数组Type *r = new Type[n+1];r[n] = 0;for(int j=n-1; j>0; j--){r[j] = r[j+1] + w[j+1];}//初始化int i = 1;//当前扩展节点所处的层bbnode *E = 0;//当前扩展节点Type Ew = 0; //扩展节点所相应的载重量//搜索子集空间树while(i!=n+1)//非叶子节点{//检查当前扩展节点的儿子节点if(Ew+w[i]<=c){AddLiveNode(H,E,Ew+w[i]+r[i],true,i+1); }//右儿子节点AddLiveNode(H,E,Ew+r[i],false,i+1);//取下一扩展节点HeapNode<Type> N;H.DeleteMax(N);//非空i = N.level;E = N.ptr;Ew = N.uweight - r[i-1];}//构造当前最优解for(int j=n; j>0; j--){bestx[j] = E->LChild;E = E->parent;}return Ew;}1.3运行结果2队列式分支限界法求解2.1算法分析在算法的循环体中,首先检测当前扩展结点的左儿子结点是否为可行结点。



算法中的最优装载问题问题描述有n个集装箱要装上1艘载重量分别为c的轮船,其中第i个集装箱的重量为wi。
最优装载问题要求确定在装载体积不受限制的情况下,将尽可能多的集装箱装上轮船,并找出一种装载方案其中@w #集装箱的重量数组@c #货船的最大载重量@n #集装箱的个数@r #未被装载的货物重量@cw #当前货船上的载重@i #搜索树的层数@bestw #最优值@bestx #最优解class Loadingdef initialize(weight,cont)@w,@c,@n=weight,cont,weight.length@r,@cw,@i,@bestw=0,0,0,0@x=Array.new@bestx=Array.newfor j in 0..@n-1@r=@r+@w[j];@bestx[j],@x[j]=0,0endprint \\"集装箱的总重量为 #@r,\\n\\"enddef MaxLoadingwhile truewhile @i<=(@n-1) and (@cw+@w[@i]<@c)@r-=@w[@i]@cw+=@w[@i]@x[@i]=1print \\"在左子树中\\",@x[@i],\\"\\n\\"@i+=1endif @i>@n-1for j in 0..@n-1@bestx[j]=@x[@i]print \'到达叶子节点\',j,\\"\\t @bestx[j]\\",@bestx[j],\\"\\n\\" end@bestw=@cwelse@r-=@w[@i];@x[@i]=0;print \'在右子树中\',@x[@i],\\"\\n\\" @i+=1endwhile @cw+@r<=@bestw@i-=1while @i>=0 and (@x[@i]==0)@r+=@w[@i];@i-=1endif @i==-1 thenprint \\"@bestw:\\",@bestwreturnend@x[@i]=0@cw-=@w[@i]@i+=1endendendendweight=[30,10,10]cont=35s=Loading.new(weight,cont)s.MaxLoading运行的结果如下:集装箱的总重量为 50,在左子树中1在右子树中0在右子树中0到达叶子节点0 @bestx[j]nil到达叶子节点1 @bestx[j]nil到达叶子节点2 @bestx[j]nil@bestw:30>Exit code: 0。

贪⼼算法之最优装载问题贪⼼算法之最优装载问题1. 问题描述有⼀批集装箱要装上⼀艘重量为c的轮船,其中集装箱i的重量为W i。
最优装载问题要求确定在装载体积不受限制的情况下,将尽可能多的集装箱装上轮船。
2. 问题分析2.1确定贪⼼策略采⽤重量最轻者先装的贪⼼选择策略,可产⽣该问题的最优解。
2.2代码求解/*** x[] 保存最优解路径数组* w[] 集装箱重量数组* c 船的载重量* n 集装箱的数量**/void Loading(int x[], int w[], int c, int n) {// 按照集装箱重量从⼩到⼤排序sort(w, n);for (int i = 1; i <= n; i++)x[i] = 0;for (int i = 1; i <= n && w[i] <= c; i++) {x[i] = 1;c -= w[i];}}2.3贪⼼选择性质设集装箱依其重量从⼩到⼤排序,(x1,x2,…,x n)是其最优解,x i={0,1},设x k是第⼀个等于1的。
(1) 如k=1,则满⾜贪⼼选择性质(2) 如k≠1,⽤x1替换x k,构造的新解同原解最优值相同,故也是最优解,满⾜贪⼼选择性质该证明⽅法只证明了任何⼀个最优解都可以转换为第⼀个集装箱上船的最优解(满⾜贪⼼策略)。
此⽅法对⼦问题同样有效,因此可以将⼀个普通最优解转化为满⾜贪⼼策略的最优解。
如(0101)⇒(1100)2.4.最优⼦结构性质最优装载问题具有最优⼦结构性质,设1⾄n个集装箱装上船的最⼤数量为T(1,n,w),则T(1,n,w)=1+T(2,n,w−w1);因T(1,n,w)是最优值,则T(2,n,w−w i)⼀定是最优值,反证法证明之反证法:如果T(2,n,w−w1)不是该问题的最优解,则存在最优值T′(2,n,w−w1)>T(2,n,w−w1),则1+T′(2,n,w−w1)=T′(1,n,w)>T(1,n,w),这与⼤前提T(1,n,w)是最优值相⽭盾,故T(2,n,w−w1)⼀定是最优值。


英语算法-回复如何使用贪心算法(Greedy Algorithm)解决最优装载问题(Knapsack Problem)。
【引言】贪心算法是一种基于局部最优选择的算法思想,可用于解决最优装载问题,即在给定容量的背包中,如何选择物品使其总价值最大。
本文将介绍如何使用贪心算法逐步解决最优装载问题,帮助读者更好地理解和应用贪心算法。
【步骤一:问题描述】首先,让我们明确最优装载问题的具体要求。
给定一个背包的容量C和N 个物品,每个物品有自己的重量w和价值v。
我们的目标是在不超过背包容量的情况下,选择物品放入背包,使得放入背包的物品的总价值最大。
【步骤二:贪心选择策略】贪心算法的核心思想是进行局部最优选择,以期望最终得到整体最优解。
对于最优装载问题,我们可以采用“单位重量价值最大”的贪心选择策略。
即优先选择单位重量价值最大的物品放入背包中,直至背包无法再放入物品。
【步骤三:算法实现】基于贪心选择策略,我们可以使用如下步骤实现算法:1. 根据物品的重量w和价值v,计算每个物品的单位重量价值vu = v / w。
2. 按照单位重量价值vu从大到小对物品进行排序。
3. 初始化当前背包的总价值val = 0和当前背包的剩余容量rc = C。
4. 逐个遍历排序后的物品列表:a. 如果当前物品的重量小于等于当前背包的剩余容量,则将该物品放入背包中,更新当前背包的总价值val和剩余容量rc。
b. 如果当前物品的重量大于当前背包的剩余容量,则放弃该物品,继续遍历下一个物品。
5. 返回最终的背包总价值val作为最优装载问题的解。
【步骤四:算法示例】接下来,我们通过一个简单的例子演示如何使用贪心算法解决最优装载问题。
假设背包容量C为10,有以下4个物品可供选择:物品1:重量w1 = 2,价值v1 = 5物品2:重量w2 = 3,价值v2 = 8物品3:重量w3 = 4,价值v3 = 9物品4:重量w4 = 5,价值v4 = 10按照贪心选择策略,首先计算每个物品的单位重量价值vu:物品1:vu1 = v1 / w1 = 5 / 2 = 2.5物品2:vu2 = v2 / w2 = 8 / 3 ≈2.67物品3:vu3 = v3 / w3 = 9 / 4 = 2.25物品4:vu4 = v4 / w4 = 10 / 5 = 2.0然后,按照单位重量价值vu从大到小对物品进行排序:物品2 > 物品1 > 物品3 > 物品4接下来,我们按照步骤三中的算法实现进行装载:初始化当前背包的总价值val = 0和剩余容量rc = 10。

最优装载一、问题描述:有一批集装箱要装上一艘载重量为c的轮船。
其中集装箱i的重量为Wi。
最优装载问题要求确定在装载体积不受限制的情况下,将尽可能多的集装箱装上轮船。
二、输入:表格一:物品的重量三、输出:图一:放入轮船的物品四、算法描述:定义存放的重量w[]、总容量为c、定义一个新数组数组内的序号定义为0,首先把数组的序号和数值打印出来,进行冒泡排序,把排序好的数组内的值打印一遍,开始往船上放物品,每放入一个物品,把这个物品的下标定义为1,并且用总容量c-w[i],当c大于0,就一直存放,直到不能放入为止。
五、算法设计:使用贪心算法首先要明白贪心算法,贪心算法以贪心为主,要达到每一步都是最优解。
于是,我先对物品的重量进行排序,在问题描述中已经得知,要将尽可能多的集装箱装上轮船,所以我按照从小到大的顺序物品排序完毕后,开始往轮船上放;在每一次放入后,刷新剩余的总容量,并将放入物品的下表定义为1,就这样依次装入,直到物品不能放入为止。
六、举例:表格二:排序后的物品重量因为轮船的容量为100,当第一个物品放入后当前背背包的容量为90,并且下标为1.表格三:第一个物品放入后当第一个物品放入后容量已经变为90,开始放入第二个物品,放入后当前总量为78,并让第二个物品下标为1。
表格四:第二个物品放入后第二个物品放入后容量由原来的90变为现在的78,准备放入第三个物品,并让第三个下标为1。
表格五:第三个物品放入后第三个物品放入后容量由原来的78变为现在的64,准备放入第四个物品,并让第四个下标为1。
表格六:第四个物品放入后第四个物品放入后容量由原来的64变为现在的49,准备放入第五个物品,并让第五个下标为1。
表格七:第五个物品放入后第五个物品放入后容量由原来的49变为现在的34,准备放入第六个物品,并让第六个下标为1。
表格八:第六个物品放入后第六个物品放入后容量由原来的34变为现在的18,准备放入第七物品,并让第七个下标为1。

最优装载问题(贪⼼)⼀、实验内容运⽤贪⼼算法解决活动安排问题(或最优装载问题)使⽤贪⼼算法解决最优装载问题。
⼆、所⽤算法基本思想及复杂度分析1.算法基本思想贪⼼算法是指在对问题求解时,总是做出在当前看来是最好的选择。
也就是说,不从整体最优上加以考虑,它所做出的仅是在某种意义上的局部最优解。
⽤局部解构造全局解,即从问题的某⼀个初始解逐步逼近给定的⽬标,以尽可能快的求得更好的解。
当某个算法中的某⼀步不能再继续前进时,算法停⽌。
2.问题分析及算法设计问题分析:(1)给定n个古董,要把它们装到装载量为c的装载船上。
(2)⾸先需要对这n个古董进⾏质量从⼩到⼤的排序。
(3)然后每次都选择最轻的,接着再从剩下的n-1件物品中选择最轻的。
(4)重复第(3)步骤,直到当前载重量⼤于装载船的最⼤装载量,停⽌装载。
(5)此时得到最优的贪⼼⽅案,记录下装载的最⼤古董数。
算法设计:(1)算法策略:把n件物品从⼩到⼤排序,然后根据贪⼼策略尽可能多的选出前i个物品,直到不能装为⽌。
(2)特例:算法复杂度分析由最优装载问题的贪⼼选择性质和最优⼦结构性质,可知将这些古董按照其重量从⼩到⼤排序,所以算法所需的计算时间为O(nlogn)。
三、源程序核⼼代码及注释(截图)四、运⾏结果五、调试和运⾏程序过程中产⽣的问题及解决⽅法,实验总结(5⾏以上)这⾥的调试,没有什么⼤问题,单纯的依次⽐较,判断,从⽽得到结果。
这次实验让我对贪⼼算法有了更深刻的认识,其主要是从问题的初始解出发,按照当前最佳的选择,把问题归纳为更⼩的相似的⼦问题,并使⼦问题最优,再由⼦问题来推导出全局最优解。
贪⼼算法虽然求的是局部最优解,但往往许多问题的整体最优解都是通过⼀系列的局部最优解的选择来达到的,所以贪⼼算法不⼀定可以得到能推导出问题的最优解,但其解法是最优解的近似解。
懂得算法的原理,还需要多去练习才能更好的掌握其⽤法。
源码:#include<iostream>#include<algorithm>#define MAXN 1000005using namespace std;int w[MAXN];//每件古董的重量int main(){int c,n;//c:载重量,n古董数int sum = 0;//装⼊古董的数量int tmp = 0;//装⼊古董的重量cin >> c >> n;for(int i= 1; i <= n; ++i)cin >> w[i];sort(w+1,w+1+n);for(int i = 1; i <= n; ++i){tmp += w[i];if(tmp <= c)++sum;elsebreak;}cout << sum << endl;return 0;}。

最优装载问题最优装载问题问题:n 个集装箱1, 2, … , n 装上轮船,集装箱i 的重量wi , 轮船装载重量限制为C,无体积限制. 问如何装使得上船的集装箱最多?不妨设每个箱子的重量w i ≤C.该问题是0-1背包问题的子问题. 集装箱相当于物品,物品重量是w i ,价值v i 都等于1,轮船载重限制C 相当于背包重量限制b .建模ni x Cx w x i i n i in i i ,...,2,11,0max 11==≤∑∑==设<x 1,x 2,...,x n > 表示解向量,x i =0,1,x i =1当且仅当第i 个集装箱装上船目标函数约束条件算法设计•贪心策略:轻者优先•算法设计:将集装箱排序,使得w1 ≤w2≤... ≤w n按照标号从小到大装箱,直到装入下一个箱子将使得集装箱总重超过轮船装载重量限制,则停止.正确性证明思路•命题:对装载问题任何规模为n 的输入实例,算法得到最优解.•设集装箱从轻到重记为1, 2, … , n.归纳基础证明对任何只含1个箱子的输入实例,贪心法得到最优解.显然正确.•归纳步骤证明:假设对于任何n个箱子的输入实例贪心法都能得到最优解,那么对于任何n+1个箱子的输入实例贪心法也得到最优解.归纳步骤证明思路N={1,2,...,n+1}, w1≤w2≤...≤w n+1正确性证明假设对于n个集装箱的输入,贪心法都可以得到最优解,考虑输入N = { 1, 2, … , n+1 }≤w2 ≤… ≤w n+1.其中w1由归纳假设,对于N' = {2, 3, …, n+1},C'= C−w1, 贪心法得到最优解I'. 令I = I '∪{1}7正确性证明(续)I (算法解)是关于N 的最优解.若不然,存在包含1 的关于N 的最优解I*(如果I* 中没有1,用1 替换I* 中的第一个元素得到的解也是最优解), 且|I*|>| I |;那么I*−{1}是N' 和C' 的解且| I*−{1}| > | I −{1} | = | I' |与I'是关于N' 和C' 的最优解矛盾.I* I小结•装载问题是0-1背包的子问题(每件物品重量为1),NP难的问题存在多项式时间可解的子问题.•贪心法证明:对规模归纳9。
最优装载问题(Optimal loading problem)最优装载问题(Optimal loading problem)Optimal loading problemProblem descriptionThere are n containers to be loaded with 1 ships with carrying capacity of C respectively, in which the weight of the first I container is wi. The optimal loading problem requires that the container be loaded with as many containers as possible in the case of unlimited loading volume and find a loading schemeinputThe input has several sets of test data (no more than 20 groups).Each set of test data has 2 lines:The first line is the container number N and the ship carrying capacity C (n<1000, c<65535);The second line has n integers W1, w2,... Wn, integers are separated by one space, and these n integers represent the weight of the n containers in turn, (0<wi, <1000, i=1,2),... (n).outputYou are required to output 3 lines of each test data in the input: The output of "Case #" in the first line, which "#" is the number of test data (starting from 1).On the second line, two integers bestn and leftc, where bestn is the maximum number of containers loaded by the vessel, and leftc is the maximum remaining load of the ship corresponding to the bestn.Output a 0-1 string x1x2 on the third line... Xn, in which x1x2... Xn is the specific loading scheme corresponding to the bestn. The xi=1 indicates that the I container is mounted on the vessel, while the xi=0 indicates that the I container is not mounted on the vessel.The loading scheme corresponding to the bestn may not be unique, such as 3 containers with a weight of 40, 10, and 40. If the carrying capacity of the vessel is 50, then only 2 containers can be loaded on board, so there are two options for loading, 110 and 011. In order to make the output results only, we agreed to n long 0-1 string to the maximum lexicographic order to meet the requirements of the loading scheme, in this case should be 110.sample input3504010405371030243540sample outputCase 120One hundred and tenCase 223Ten thousand and one hundred#include <iostream.h>//template<class int>Class MaxHeap;//template<class int>Class HeapNode;Class bbnode{Friend, void, AddLiveNode (MaxHeap&, bbnode*, int, int, int);Friend, int, MaxLoading (int*, int, int, int *);//friend class adjacencygraph;Private:Bbnode *parent; / / pointer to the parent node.Int Lchild; / / left son node mark};//////////////////////////////////////////////////////////////////// /////template<class int>Class HeapNode{Friend, void, AddLiveNode (MaxHeap&, bbnode*, int, int, int);Friend, int, MaxLoading (int*, int, int, int *);Public:Operator int () const {return uweight;}/ / private:Bbnode *ptr; / / to live nodes in the corresponding node subset tree pointerInt uweight; / / live node priority - boundInt level; / / live nodes in subset tree layers in number};//template <class int>类maxheap {朋友AddLiveNode(maxheap无效,bbnode *,int,int,int);朋友int Maxloading(int,int,int,int *);私人:int m;int SZ;heapnode * HX;公共:maxheap(int SZ){HX =新heapnode【尺码】;m,0;}/ / ~ maxheap() {删除[ ] HX;}插入(heapnode n){HX [M + 1 ] = N;HX [ M ] n.ptr ptr = + 1;HX [M + 1 ]。
货物装载优化方法及应用探究一、引言货物装载优化是物流行业中的关键问题之一,它直接影响物流成本、时效等方面。
因此,如何通过科学的方法减少货物装载过程中出现的问题,优化装载方案,提高物流效率和降低成本,成为当前物流业面临的重大问题。
二、货物装载问题分析1. 装载顺序问题针对不同的货物需求和运输条件,运输车辆上的货物装载顺序应该有所区别。
否则可能出现在卸货时形成交集,造成货物混乱,影响卸载时效。
2. 承载限制问题每辆运输车辆对于所能承载的重量和体积都有明确的限制。
如果不合理地将货物装载到车厢中,将使得运输车辆在行驶过程中出现滚动、不平衡的现象,从而影响交通安全。
3. 货物固定问题运输车辆上的货物在行驶过程中可能会出现晃动、摇晃等现象,如不能很好的固定住货物,这样就会影响货物的安全性和配送质量。
同时,对于货物固定采取不合理的方法会导致货物损坏或者车辆受损。
三、货物装载优化方法1. 货物分组优化法其中一个解决运输车装载顺序的方法是将货物分组,依据各组货物的卸车目的地、内部的物种及数量等特性,对它们进行装载。
通过分组减少分组货物之间的交叉卸货次数,保证装载的货物在卸货时具有合理的顺序和方便的运输。
2. 模拟优化法尤其是在装载车辆数量较多时,对于人工的优化算法来说存在一定程度上的无效性和低效性。
目前,很多生产企业已经引入各种装载的模拟软件来实现货物的自动优化。
在运用这些软件的时候,只需输入货物量、车辆数和运输信息等数据,程序即可自动进行货物装载方案优化,并得出最优方案。
3. 有效利用空间对于承载限制等装载问题,则需要在货物上装载时合理考虑并有效利用车辆运输空间。
可以通过控制装载高度、拉伸牢固以及选择不同的运输装置等措施。
例如,利用高低搭配安排货物的装载,以满足所装载物品体积要求和车辆限制标准等。
四、应用探究随着物流行业的不断发展,货物装载优化方法的应用不断变化。
如今,各个物流公司普遍采用智能装载优化系统,用于提高装载效率,降低运输成本。
回溯法——装载问题问题描述: 有⼀批共n个集装箱要装上2艘载重量分别为c1和c2的轮船,其中集装箱i的重量是wi,且不能超,即Σwi<=c1+c2。
算法思想: ——在给定的装载问题有解的情况下 最优装载⽅案:⾸先将第⼀艘轮船尽可能的装满; 然后将剩余的集装箱装上第⼆艘轮船。
将第⼀艘轮船尽可能的装满等价于选取全体集装箱的⼀个⼦集,使该⼦集中集装箱重量之和最接近c1。
算法设计: 先考虑装载⼀艘轮船的情况,依次讨论每个集装箱的装载情况,共分为两种,要么装(1),要么不装(0),因此很明显其解空间树可以⽤⼦集树来表⽰。
在算法Maxloading中,返回不超过c的最⼤⼦集和,但是并没有给出到达这个最⼤⼦集和的相应⼦集,稍后完善。
在算法Maxloading中,调⽤递归函数Backtrack(1)实现回溯搜索。
Backtrack(i)搜索⼦集树中的第i层⼦树。
在算法Backtrack中,当i>n时,算法搜索到叶结点,其相应的载重量为cw,如果cw>bestw,则表⽰当前解优于当前的最优解,此时应该更新bestw。
算法Backtrack动态地⽣成问题的解空间树。
在每个结点处算法花费O(1)时间。
⼦集树中结点个数为O(2^n),故Backtrack所需的时间为O(2^n)。
另外Backtrack还需要额外的O(n)的递归栈空间。
算法描述:1 template <class Type>2class Loading3 {4 friend Type MaxLoading(Type [],Type,int);5private:6void Backtrack(int i);7int n; //集装箱数⽬8 Type * w, //集装箱重量数组9 c, //第⼀艘轮船的载重量10 cw, //当前载重量11 bestw; //当前最优载重量12 };1314 template <class Type>15void Loading<Type>::Backtrack(int i) //回溯搜索16 { //搜索第i层结点17if(i>n) //到达叶结点18 {19if(cw>bestw)20 bestw = cw;21return;22 }23if(cw+w[i] <= c) //搜索⼦树24 {25 cw += w[i]; //当前载重量增加正考虑对象的重量26 Backtrack(i+1); 27 cw -= w[i]; //递归返回上⼀层时,记得减去刚考虑对象的集装箱重量28 }29 Backtrack(i+1); //递归搜索第i+1层30 }3132 template <class Type>33 Type MaxLoading(Type w[],Type c,int n) //返回最优载重量34 {35 Loading<Type> X; //初始化36 X.w = w;37 X.c = c;38 X.n = n;39 X.bestw = 0; //当前最优载重量的初值赋为040 X.cw = 0;41 X.Backtrack(1); //计算最优载重量————调⽤递归函数,实现回溯搜索42return X.bestw;43 }上界函数: 引⼊剪枝函数,⽤于剪去不含最优解的⼦树:即当cw(当前载重量)+r(未考察对象的总重量)<bestw(当前的最优载重量)时当前⼦树不可能包含最优解,直接减掉。
优化装载案例分析报告
装载优化技术是指通过合理的装载方案,使得货物能够最大限度地利用运输工具的容量,以提高运输效率和降低成本。
下面针对某物流公司在装载方案上存在的问题进行分析,并提出优化建议。
问题分析:
1. 货物装载不合理。
目前公司的货物装载主要依靠人工操作,由于人工操作可能存在主观因素,无法保证最优的装载方案。
因此,装载效率低,容易造成货物损坏和浪费运输空间。
2. 载重过大。
在装载货物时,有时可能会将货物的总重量超过运输工具的承载极限,这样容易导致运输事故发生,危害货物和车辆的安全。
优化建议:
1. 引入装载优化软件。
通过使用装载优化软件,可以根据货物的体积、重量等因素,自动生成最优的装载方案。
软件能够实时优化装载方案,减少空间浪费和货物损坏的风险。
2. 分析运输工具的承载能力。
在制定装载方案时,应对运输工具的承载能力进行准确的评估,合理控制货物的总重量。
可以通过称重等手段,确保货物的重量不超过运输工具的承载极限。
3. 提高装载效率。
在进行货物装载时,应尽可能地减少装载和卸载时间,提高装载效率。
可以通过优化装卸工序、配备必要的装卸工具等方式,提高装载效率,降低运输成本。
通过优化装载方案,可以有效提高运输效率,降低运输成本。
装载优化技术的引入可以减少人为因素对装载效果的影响,提
高装载的准确性和稳定性。
同时,合理控制货物的总重量,可以保证货物和车辆的安全。
只有充分发挥装载优化技术的作用,才能在提高货物运输效率和降低成本方面取得更好的效果。