实验报告:贪心算法--最优装载
- 格式:doc
- 大小:147.50 KB
- 文档页数:3
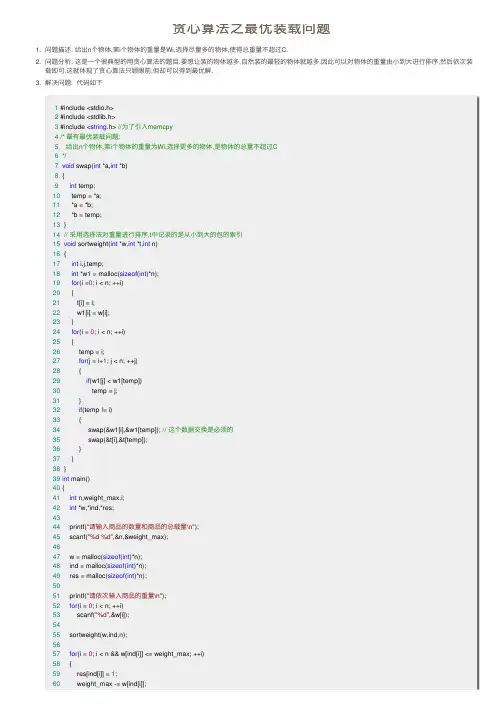
贪⼼算法之最优装载问题1. 问题描述: 给出n个物体,第i个物体的重量是Wi,选择尽量多的物体,使得总重量不超过C.2. 问题分析: 这是⼀个很典型的⽤贪⼼算法的题⽬.要想让装的物体越多,⾃然装的最轻的物体就越多.因此可以对物体的重量由⼩到⼤进⾏排序,然后依次装载即可.这就体现了贪⼼算法只顾眼前,但却可以得到最优解.3. 解决问题: 代码如下4. 1 #include <stdio.h>2 #include <stdlib.h>3 #include <string.h> //为了引⼊memcpy4/* 最有最优装载问题:5给出n个物体,第i个物体的重量为Wi,选择更多的物体,是物体的总量不超过C6*/7void swap(int *a,int *b)8 {9int temp;10 temp = *a;11 *a = *b;12 *b = temp;13 }14// 采⽤选择法对重量进⾏排序,t中记录的是从⼩到⼤的包的索引15void sortweight(int *w,int *t,int n)16 {17int i,j,temp;18int *w1 = malloc(sizeof(int)*n);19for(i =0; i < n; ++i)20 {21 t[i] = i;22 w1[i] = w[i];23 }24for(i = 0; i < n; ++i)25 {26 temp = i;27for(j = i+1; j < n; ++j)28 {29if(w1[j] < w1[temp])30 temp = j;31 }32if(temp != i)33 {34 swap(&w1[i],&w1[temp]); // 这个数据交换是必须的35 swap(&t[i],&t[temp]);36 }37 }38 }39int main()40 {41int n,weight_max,i;42int *w,*ind,*res;4344 printf("请输⼊商品的数量和商品的总载量\n");45 scanf("%d %d",&n,&weight_max);4647 w = malloc(sizeof(int)*n);48 ind = malloc(sizeof(int)*n);49 res = malloc(sizeof(int)*n);5051 printf("请依次输⼊商品的重量\n");52for(i = 0; i < n; ++i)53 scanf("%d",&w[i]);5455 sortweight(w,ind,n);5657for(i = 0; i < n && w[ind[i]] <= weight_max; ++i)58 {59 res[ind[i]] = 1;60 weight_max -= w[ind[i]];61 }62 printf("贪⼼算法求解后的结果是:\n");63for(i = 0; i < n; ++i)64 {65 printf("%d ",res[i]);66 }67 printf("\n");68return0;69 }4. 程序分析: 由于不要改变原始物体重量的值,所以在排序的时候要另外再开辟⼀个数组存储重量.并且另外开辟ind[]存放索引记录装载的顺序.ind[]存放的是重量数组中每个元素在这组数组中⼤⼩的顺序(索引).怎样在排序时记录索引需要在练习排序的时候注意下.。



XXXX 大学计算机学院实验报告计算机学院2017级软件工程专业 5 班指导教师
学号姓名2019年10 月28 日成绩
实验内容、上机调试程序、程序运行结果
System.out.print(weight[i]+" ");
}
System.out.println();
//从控制台获取集装箱的最大重量
System.out.println("请输入集装箱的最大重量:");
Scanner s = new Scanner(System.in);
maxWeight=s.nextInt();
System.out.print("可装入的集装箱有:");
//将一批集装箱装上一艘重量为80的轮船。
在装载体积不受限制的情况下,将尽可能多的集装箱装上轮船。
(重量从小到大装)
for(int k=0;k<weight.length;k++){
sumWeight += weight[k];
if(sumWeight<=maxWeight){
System.out.print(weight[k]+"kg ");
}
}
}
}
②完成效果。

贪⼼算法之最优装载问题贪⼼算法之最优装载问题1. 问题描述有⼀批集装箱要装上⼀艘重量为c的轮船,其中集装箱i的重量为W i。
最优装载问题要求确定在装载体积不受限制的情况下,将尽可能多的集装箱装上轮船。
2. 问题分析2.1确定贪⼼策略采⽤重量最轻者先装的贪⼼选择策略,可产⽣该问题的最优解。
2.2代码求解/*** x[] 保存最优解路径数组* w[] 集装箱重量数组* c 船的载重量* n 集装箱的数量**/void Loading(int x[], int w[], int c, int n) {// 按照集装箱重量从⼩到⼤排序sort(w, n);for (int i = 1; i <= n; i++)x[i] = 0;for (int i = 1; i <= n && w[i] <= c; i++) {x[i] = 1;c -= w[i];}}2.3贪⼼选择性质设集装箱依其重量从⼩到⼤排序,(x1,x2,…,x n)是其最优解,x i={0,1},设x k是第⼀个等于1的。
(1) 如k=1,则满⾜贪⼼选择性质(2) 如k≠1,⽤x1替换x k,构造的新解同原解最优值相同,故也是最优解,满⾜贪⼼选择性质该证明⽅法只证明了任何⼀个最优解都可以转换为第⼀个集装箱上船的最优解(满⾜贪⼼策略)。
此⽅法对⼦问题同样有效,因此可以将⼀个普通最优解转化为满⾜贪⼼策略的最优解。
如(0101)⇒(1100)2.4.最优⼦结构性质最优装载问题具有最优⼦结构性质,设1⾄n个集装箱装上船的最⼤数量为T(1,n,w),则T(1,n,w)=1+T(2,n,w−w1);因T(1,n,w)是最优值,则T(2,n,w−w i)⼀定是最优值,反证法证明之反证法:如果T(2,n,w−w1)不是该问题的最优解,则存在最优值T′(2,n,w−w1)>T(2,n,w−w1),则1+T′(2,n,w−w1)=T′(1,n,w)>T(1,n,w),这与⼤前提T(1,n,w)是最优值相⽭盾,故T(2,n,w−w1)⼀定是最优值。

贪⼼法之最优装载问题概念:当⼀个问题具有最优⼦结构性质时,可⽤动态规划算法,有时会有更简单有效的算法,那就是贪⼼算法,贪⼼算法是通过⼀系列的选择来得到问题的解,贪⼼算法并不从整体最优上加以考虑,所做的选择只是在某种意义上的局部最优解。
但对范围相当⼴的许多问题能产⽣整体最优解。
在⼀些情况下,即使贪⼼算法不能得到整体最优解,但其最终结果却是最优解的很好的近似解。
贪⼼算法的基本要素:贪⼼选择性质:所求解的问题的整体最优解可以通过⼀系列局部最优的选择来,即贪⼼选择达到。
贪⼼选择所依赖的是以前所做过的选择,⽽对以后所做的选择没有关系。
最优⼦结构性质:⼀个问题的最优解包含其⼦问题的最优解。
贪⼼算法与动态规划的区别:动态规划是通过⾃底向上的⽅式解决⼦问题,贪⼼算法是通过⾃顶向下的迭代⽅式做出贪⼼选择,求解问题的最优解。
两共同点是都具有最优⼦结构性质。
最优装载问题:某艘船的载重量为C,每件物品的重量为wi,要将尽量多的物品装⼊到船上。
分析:贪⼼策略:每次都选择最轻的,然后再从剩下的n-1件物品中选择最轻的。
算法策略:把n件物品从⼩到⼤排序,然后根据贪⼼策略尽可能多的选出前i个物品,直到不能装为⽌。
这个问题⽐部分背包问题还简单,先拿轻的再拿重的可以保证最后物品装的最多。
代码如下:#include<iostream>#include<algorithm>#define MAXN 10000using namespace std;int main(){int c,n; //c:船的最⾼载重量 n:古董数量int sum=0,weight=0; //sum:装⼊的古董数量 weight:装⼊的古董重量int w[MAXN]; //单个古董对应的重量cout<<"请输⼊最⾼载重量和需载的古董数⽬:"<<endl;cin>>c>>n;cout<<"请分别输⼊这些古董的重量:"<<endl;for(int i=1;i<=n;++i)cin>>w[i];sort(w+1,w+1+n);for(int i = 1 ; i<=n ; i++){weight += w[i]; //先将重量加进去if(weight >= c){if(weight == c) //恰好装满时sum = i;elsesum = i-1; //超重了,需要减去⼀个break;}}cout<<"最多可以装"<<sum<<"个"<<endl;for(int i=1;i<=sum;++i)cout<<w[i]<<"";return0;}View Code程序运⾏结果:参考:王晓东《算法设计与分析》。

最优装载问题(贪⼼)⼀、实验内容运⽤贪⼼算法解决活动安排问题(或最优装载问题)使⽤贪⼼算法解决最优装载问题。
⼆、所⽤算法基本思想及复杂度分析1.算法基本思想贪⼼算法是指在对问题求解时,总是做出在当前看来是最好的选择。
也就是说,不从整体最优上加以考虑,它所做出的仅是在某种意义上的局部最优解。
⽤局部解构造全局解,即从问题的某⼀个初始解逐步逼近给定的⽬标,以尽可能快的求得更好的解。
当某个算法中的某⼀步不能再继续前进时,算法停⽌。
2.问题分析及算法设计问题分析:(1)给定n个古董,要把它们装到装载量为c的装载船上。
(2)⾸先需要对这n个古董进⾏质量从⼩到⼤的排序。
(3)然后每次都选择最轻的,接着再从剩下的n-1件物品中选择最轻的。
(4)重复第(3)步骤,直到当前载重量⼤于装载船的最⼤装载量,停⽌装载。
(5)此时得到最优的贪⼼⽅案,记录下装载的最⼤古董数。
算法设计:(1)算法策略:把n件物品从⼩到⼤排序,然后根据贪⼼策略尽可能多的选出前i个物品,直到不能装为⽌。
(2)特例:算法复杂度分析由最优装载问题的贪⼼选择性质和最优⼦结构性质,可知将这些古董按照其重量从⼩到⼤排序,所以算法所需的计算时间为O(nlogn)。
三、源程序核⼼代码及注释(截图)四、运⾏结果五、调试和运⾏程序过程中产⽣的问题及解决⽅法,实验总结(5⾏以上)这⾥的调试,没有什么⼤问题,单纯的依次⽐较,判断,从⽽得到结果。
这次实验让我对贪⼼算法有了更深刻的认识,其主要是从问题的初始解出发,按照当前最佳的选择,把问题归纳为更⼩的相似的⼦问题,并使⼦问题最优,再由⼦问题来推导出全局最优解。
贪⼼算法虽然求的是局部最优解,但往往许多问题的整体最优解都是通过⼀系列的局部最优解的选择来达到的,所以贪⼼算法不⼀定可以得到能推导出问题的最优解,但其解法是最优解的近似解。
懂得算法的原理,还需要多去练习才能更好的掌握其⽤法。
源码:#include<iostream>#include<algorithm>#define MAXN 1000005using namespace std;int w[MAXN];//每件古董的重量int main(){int c,n;//c:载重量,n古董数int sum = 0;//装⼊古董的数量int tmp = 0;//装⼊古董的重量cin >> c >> n;for(int i= 1; i <= n; ++i)cin >> w[i];sort(w+1,w+1+n);for(int i = 1; i <= n; ++i){tmp += w[i];if(tmp <= c)++sum;elsebreak;}cout << sum << endl;return 0;}。

一、实验背景算法装载问题(Bin Packing Problem)是组合优化领域中的一个经典问题,主要研究如何将一组物品装入有限数量的容器中,使得容器中的物品总重量不超过容器的容量,同时尽可能减少容器的数量。
该问题在实际应用中具有广泛的意义,如物流运输、资源分配、生产计划等领域。
二、实验目的1. 了解算法装载问题的基本概念和特点;2. 掌握几种常用的算法装载问题的解决方法;3. 通过实验验证不同算法在解决算法装载问题时的性能;4. 分析算法的优缺点,为实际应用提供参考。
三、实验内容1. 实验环境操作系统:Windows 10编程语言:Python 3.8实验工具:Pandas、Numpy、Scipy2. 实验方法(1)遗传算法遗传算法是一种模拟自然选择和遗传学原理的搜索启发式算法。
在算法装载问题中,可以将物品和容器看作基因,通过交叉、变异等操作,不断优化解的质量。
(2)贪心算法贪心算法是一种在每一步选择中都采取当前最优策略的算法。
在算法装载问题中,可以根据物品的重量或容器的容量,对物品进行排序,然后依次将物品装入容器。
(3)动态规划动态规划是一种将复杂问题分解为子问题,并存储子问题的解的方法。
在算法装载问题中,可以根据物品的重量和容器的容量,计算最优解。
3. 实验数据实验数据来源于一组具有不同重量和数量的物品,以及不同容量和数量的容器。
四、实验结果与分析1. 遗传算法实验结果表明,遗传算法在解决算法装载问题时具有较高的求解能力。
随着迭代次数的增加,解的质量逐渐提高,但求解时间较长。
2. 贪心算法贪心算法在解决算法装载问题时具有较快的求解速度,但解的质量相对较差。
在部分情况下,贪心算法得到的解甚至无法满足所有容器的容量要求。
3. 动态规划动态规划在解决算法装载问题时具有较高的求解质量,但求解时间较长。
对于大型问题,动态规划可能无法在合理时间内得到最优解。
五、结论通过对遗传算法、贪心算法和动态规划在算法装载问题中的应用实验,得出以下结论:1. 遗传算法具有较高的求解能力,但求解时间较长;2. 贪心算法求解速度快,但解的质量较差;3. 动态规划求解质量高,但求解时间较长。

一、实验目的通过本次实验,使学生对贪心算法的概念、基本要素、设计步骤和策略有更深入的理解,掌握贪心算法的原理和应用,并能够运用贪心算法解决实际问题。
二、实验内容本次实验主要涉及以下两个问题:1. 使用贪心算法解决单起点最短路径问题;2. 使用贪心算法解决小船过河问题。
三、实验原理1. 贪心算法贪心算法(又称贪婪算法)是一种在每一步选择中都采取当前最优的选择,从而希望导致结果是全局最优的算法。
贪心算法在每一步只考虑当前的最优解,不保证最终结果是最优的,但很多情况下可以得到最优解。
2. 单起点最短路径问题单起点最短路径问题是指在一个有向无环图中,从某个顶点出发,找到到达其他所有顶点的最短路径。
3. 小船过河问题小船过河问题是指一群人需要划船过河,船只能容纳两个人,过河后需要一人将船开回,问最少需要多久让所有人过河。
四、实验步骤及说明1. 创建图结构,包括顶点数组和边信息。
2. 使用Dijkstra算法求解单起点最短路径问题,得到最短路径和前驱顶点。
3. 使用贪心算法找到两点之间的最短距离,并更新距离和前驱顶点信息。
4. 遍历所有顶点,找到未纳入已找到点集合的距离最小的顶点,并更新其距离和前驱顶点。
5. 最终输出从源顶点到达其余所有点的最短路径。
6. 使用贪心算法解决小船过河问题,按照以下步骤进行:(1)计算所有人过河所需的总时间;(2)计算每次划船往返所需时间;(3)计算剩余人数;(4)重复(2)和(3)步骤,直到所有人过河。
五、实验结果与分析1. 单起点最短路径问题实验中,我们选取了有向无环图G,其中包含6个顶点和8条边。
使用贪心算法和Dijkstra算法求解单起点最短路径问题,得到的实验结果如下:- 贪心算法求解单起点最短路径问题的时间复杂度为O(V^2),其中V为顶点数;- Dijkstra算法求解单起点最短路径问题的时间复杂度为O(V^2),其中V为顶点数。
2. 小船过河问题实验中,我们选取了一群人数为10的人过河,船每次只能容纳2人。

贪心法求解最佳装载背包问题描述:对于容量为c的背包进行装载,从n个物品中选择装入背包的物品,每个物品i的重量和价值分别为wi和pi。
在背包中物品的总重量不超过背包容量的前提下,求装入物品价值最高的装载法。
输入:5 20 //物品的数量和背包的容量6 3 //第一个物品的重量和价值2 5 //…3 810 67 4输出:1110.714286算法如下:#include <stdio.h>#include <stdlib.h>struct goodinfo//物品结构体{float p;//价值float w;//重量float x;//数量int flag;//标志变量};void Insertionsort(struct goodinfo goods[],int n)//将物品根据价值排序{int i,j;for(j=2;j<=n;j++){goods[0]=goods[j];//保存比较的对象i=j-1;while(goods[0].p>goods[i].p)//找到位置后退出{goods[i+1]=goods[i];//错位i--;}goods[i+1]=goods[0];//找到位置后将比较的对象覆盖}}void bag(struct goodinfo goods[],float M,int n){float cu;//剩余空间int i,j;for(i=1;i<=n;i++)goods[i].x=0;//初始化cu=M;//初始化for(i=1;i<=n;i++){if(goods[i].w>cu)break;goods[i].x=1;cu=cu-goods[i].w;}if(i<=n)goods[i].x=cu/goods[i].w;//将物品分割for(j=2;j<=n;j++)//按照物品的编号排序,便于输出goods[0]=goods[j];i=j-1;while(goods[0].flag<goods[i].flag){goods[i+1]=goods[i];i--;}goods[i+1]=goods[0];}printf("最优解为:\n");for(i=1;i<=n;i++){printf("第%d件物品要放:%f\n",i,goods[i].x);}}int main(){int j=1,n,i;float M;while(j)system("cls");printf("输入物品的总数:");scanf("%d",&n);struct goodinfo goods[n+1];//动态定义结构体数组的大小printf("背包最大容量:");scanf("%f",&M);for(i=1;i<=n;i++){goods[i].flag=i;printf("weight input:");scanf("%f",&goods[i].w);printf("price input:");scanf("%f",&goods[i].p);goods[i].p/=goods[i].w;}Insertionsort(goods,n);bag(goods,M,n);printf("press <1> to run again\npress <0> to exit\n请输入操作码:");scanf("%d",&j);}return 0; }。

实验五箱子装载问题一、实验目的二、实验内容及要求1、使用贪心算法、回溯法、分支限界法解决箱子装载问题。
(任选两种)2、通过上机实验进行算法实现。
3、保存和打印出程序的运行结果,并结合程序进行分析,上交实验报告。
三、实验原理 回溯法原理:从开始结点出发,以深度优先方式搜索整个解空间。
这个节点成为活结点,同时也成为 当前的扩展节点。
在当前的扩展节点处,搜索向纵深方向一致一个新节点。
贪心算法原理:贪心算法通过一系列的选择来得到问题的解。
他所做的每一个选择都是当前状态下局部 最好选择,即贪心选择。
四、程序代码(1)贪心算法#include <stdio.h>#include <stdlib.h>swap( int &x, int &y){ // 交换 int t;t = x;x = y;y = t;sort( int w[], int t[], int n) // 排序,有小到大1、 理解和复习所学各种算法的概念;2、 掌握和复习所学各种算法的基本要素;3、 掌握各种算法的优点和区别;4、 通过应用范例掌握选择最佳算法的设计技巧与策略;void }voidfor int int (int m = 0; m< n; m++) //为每个物品编序号 t [m] = m; i, j; lastExcha ngeln dex; n - 1; while (i>0){ lastExcha ngeln dex = 0; for (j = 0; j<i; j++){ if ( w[j + 1]< w[j]){ swap (wj + 1], w[j]); //物品的重量交换 } voidlastExcha ngeln dex = j; swap (t[j], t[j + 1]);丨 } } i = lastExcha ngeln dex; load ing( int x[], int 吨,int c, int n, int * t) // 最有装载 sort( w for ( int t, n); i = 0; i< n; i++) x[i] = 0; for ( int j = 0; j< x[ t [j]] = 1; c -= w[t[j]]; } } int mian(){ int n, c;printf("请输入物品个数: scanf( "%d", &n); printf("请输入最大容量: scanf( "%d", &c); x[200]; //存储物品编号 w[200]; //存储每个物品重量(int i = 0; i<n; i++){ printf("请输入第%d 个物品重量:“,i); scanf( "%d", &w[i]); n&&[ t [j]] <= c; j++){// 装入 "); "); int int for }l int *t = new int [n]; //物品是否装入(int j = 0; j<n; j++) x[j] = 0; //初始化物品均未装入 loadi ng(x, w, c, n, t);printf("装入物品编号为:“); forfor ( int k = 0; k<n; k++) if (x[k] == 1) Iprintf( "%d " , t[k]); return 0;(2)回溯法#inelude <stdio.h> #inelude <stdlib.h>#defi ne numlOO//限界函数rw = rw + w[i];return (rw + cw);r//递归求解void load in gRec( int t){int i;if (ew>bestw){bestw = cw;for (i = 1; i <= n; i++)bestx[i] = x[i];};return ;}else {if (cw + w[ t ]<c1) {x[t] = 1;if ( t >n) //到底叶子节点,求得一个可行解 int int int int bestx[ num = { 0 };w[ num;x[ num;bestw = 0;// // //存放最优解集装箱重量丨 解 //最优装船重量 int int cw = 0; // n ; 当前已装船重量 集装箱个数// int e1;// int e2;// 第一船的重量 第二船的重量int bound( int t) { Iintrw = 0;// 选择当前节点又分支的剩余集装箱重之和 for (int i = t + 1; t<n; t ++)// 上界 //当前解比以前解更优 //左分支满足约束条件cw = cw + w[ t];loadingRec( t + 1); //前进继续搜索下一节点|//回溯;回复CW 与x[t] 的值[CW = CW - w[ t];[x[t] = 0;5 loadingRec( t + 1);I printf( “第一船的最优装载量为: %d\n", bestw);printf("第一船的最优解为");II for ( int i = 1; i <= n; i++)] printf(~"%d " , bestx[i]);//求剩余集装箱的重量Iint cw2 = 0; I for (int i = 0; i <= n; i++) if (bestx[i] == 0) cw2 += w[i];五、结果运行与分析(1)贪心算法1_ jfiML 弋«Lhe"伽i?\AppLJdl 酣hoTiJ 啊忧•打ee\bdumplH0p< 1 jexe"(2)回溯法|nt main()门I n = 4;' ] w[1] = 4, w[2] = 5, w[3] = 3, w[4] = 2; I c1 = 8; 〃集装箱个数I 〃集装箱重量I c2 = 7; I cw =可 I bestw = 0;jloadi ngRec(1); //第一个船重量]//第二个船重量 //从第一个集装箱开始装箱 if (bound( t )>bestw)〃右分支满足限界条件I六、心得与体会这次实验可以看做是对前几次实验的回顾,使用的算法是相同的,只是解决的问题改变了,只要对算法理解,解决起来这些问题就会得心应手。
贪⼼算法-装载问题贪⼼选择算法为算法分析中⼀种常⽤算法,通过⼀系列的选择来得到⼀个问题的解。
它所作的每⼀个选择都是当前状态下某种意义的最好选择,即贪⼼选择。
希望通过每次所作的贪⼼选择导致最终结果是问题的⼀个最优解。
这种启发式的策略并不总能奏效,然⽽在许多情况下确能达到预期的⽬的。
对于可利⽤贪⼼算法解决的问题需要同时满⾜:最优⼦结构性质和贪⼼选择性质。
1.贪⼼选择性质所谓贪⼼选择性质是指所求问题的整体最优解可以通过⼀系列局部最优的选择,即贪⼼选择来达到。
这是贪⼼算法可⾏的第⼀个基本要素,也是贪⼼算法与动态规划算法的主要区别。
在动态规划算法中,每步所作的选择往往依赖于相关⼦问题的解。
因⽽只有在解出相关⼦问题后,才能作出选择。
⽽在贪⼼算法中,仅在当前状态下作出最好选择,即局部最优选择。
然后再去解作出这个选择后产⽣的相应的⼦问题。
贪⼼算法所作的贪⼼选择可以依赖于以往所作过的选择,但决不依赖于将来所作的选择,也不依赖于⼦问题的解。
正是由于这种差别,动态规划算法通常以⾃底向上的⽅式解各⼦问题,⽽贪⼼算法则通常以⾃顶向下的⽅式进⾏,以迭代的⽅式作出相继的贪⼼选择,每作⼀次贪⼼选择就将所求问题简化为⼀个规模更⼩的⼦问题。
对于⼀个具体问题,要确定它是否具有贪⼼选择性质,我们必须证明每⼀步所作的贪⼼选择最终导致问题的⼀个整体最优解。
通常可以⽤我们在证明活动安排问题的贪⼼选择性质时所采⽤的⽅法来证明。
⾸先考察问题的⼀个整体最优解,并证明可修改这个最优解,使其以贪⼼选择开始。
⽽且作了贪⼼选择后,原问题简化为⼀个规模更⼩的类似⼦问题。
然后,⽤数学归纳法证明,通过每⼀步作贪⼼选择,最终可得到问题的⼀个整体最优解。
其中,证明贪⼼选择后的问题简化为规模更⼩的类似⼦问题的关键在于利⽤该问题的最优⼦结构性质。
2.最优⼦结构性质当⼀个问题的最优解包含着它的⼦问题的最优解时,称此问题具有最优⼦结构性质。
问题所具有的这个性质是该问题可⽤动态规划算法或贪⼼算法求解的⼀个关键特征。
计算机算法与设计实验内容:贪心算法-最优装载问题描述:有一批集装箱要装上一艘载重量为c 的轮船。
其中集装箱i 的重量为Wi ,最优装载问题要求在装载体积不受限制的情况下,将尽可能多的集装箱装上轮船。
问题分析:该问题可形式化描述为:∑=n i ix 1maxc x w n i ii ≤∑=1 {}n i x i ≤≤∈1,1,0算法描述:最优装载问题可用贪心算法求解。
采用重量最轻者先装的贪心选择策略,可产生最优装载问题的最优解。
具体算法描述如下:Template<class Type>Void Loading(int x[],Type w[],Type c ,int n){int *t = new int [n+1];Sort(w,t,n);for(int i =1;i<+n;i++){x[i] = 0;}for (int i = 1;i<=n&&w[t[i]]<=c;i++){x[t[i]] = 1;c-= w[t[i]];}}所需计算时间为O(nlogn)运行结果:另选一组数据输入:详细设计:#include <iostream>using namespace std;const int N = 100;template<class Type>void Loading(int x[],Type w[], Type c, int n) {int *t = new int [n+1];//Sort(w, t, n); //调用SelectSort函数for(int k=1; k<=n; k++)x[k] = 0;//初始化数组x[]}for(int i=1; i<=n && w[t[i]]<=c; i++){x[t[i]] = 1; //经判断该集装箱可以装入c -= w[t[i]]; //轮船可栽重相应减少}}template<class Type>void Sort(Type w[],int *t,int n){Type tempArray[N+1],temp;int min;memcpy(tempArray,w,(n+1)*sizeof(Type));//将w数组数据拷贝到数组tempArray中for(int e=1;e<=n;e++){t[e] = e;for(int i=1;i<n;i++) //类冒泡算法,将集装箱按重量从小到大排列{min=i;for(int j=i+1;j<=n;j++){if(tempArray[min]>tempArray[j]){min=j;}}Swap(tempArray[i],tempArray[min]);Swap(t[i],t[min]);}}template <class Type>void Swap(Type &x,Type &y) //swap函数{Type temp = x;x = y;y = temp;}int main(){float c ; //l轮船总载重int x[N+1]; //装载结果(0与1分别表示是否装入int a ;//集装箱数量cout <<"/////////////贪心算法求解最优装载问题////////////////////"<<endl;cout<<"轮船载重为:";cin>>c;cout<<"集装箱数量:";cin>>a;float *m = new float [a];cout<<"待装物品的重量分别为:"<<endl;for(int i = 1;i<=a;i++){cout<<"请输入第"<<i<<"个集装箱的重量:";cin>>m[i];}cout<<endl;cout<<"集装箱列表:"<<endl;for(int j=1; j<=a; j++){cout<<m[j]<<"\t";}cout<<endl;Loading(x,m,c,a);cout<<"对应的贪心选择结果为:"<<endl;for(int f=1; f<=a; f++){ if(x[f]==0||x[f]==1)cout<<x[f]<<"\t";}cout<<endl;cout<<"集装箱最优装载情况:"<<endl;for(int b=1; b<=a; b++){if (x[b]==0||x[b]==1){if (x[b]==0){cout <<"第"<<b<<"个集装箱不装入"<<endl;}else{cout<<"第"<<b<<"个集装箱装入"<<endl;}}}cout<<"///////////////////////结束////////////////////////////"<<endl;system("pause");return 0;}。
一、实验目的1. 了解装载问题的基本概念和特点;2. 掌握解决装载问题的常用算法;3. 通过实验验证不同算法的效率和适用性;4. 分析装载问题的实际应用场景。
二、实验背景装载问题是指在一个容量为V的容器中,如何将一组物品按照一定的顺序装载进去,使得总装载量最大。
该问题在物流、生产调度等领域具有广泛的应用。
三、实验内容1. 装载问题概述(1)问题描述:给定一组物品的重量和容量限制,求出在不超过容量限制的情况下,物品的总重量最大;(2)问题特点:组合优化问题,存在多个局部最优解。
2. 解决装载问题的常用算法(1)贪心算法:每次选择当前未装载物品中重量与容量比最大的物品;(2)动态规划:根据已装载物品的重量和容量,确定剩余物品的装载顺序;(3)遗传算法:模拟自然选择和遗传变异,寻找最优装载方案。
3. 实验设计(1)数据准备:生成一定数量的物品,设定容量限制;(2)算法实现:分别实现贪心算法、动态规划算法和遗传算法;(3)结果分析:对比不同算法的运行时间和装载量。
四、实验步骤1. 数据准备(1)设定物品数量:n;(2)设定容量限制:V;(3)生成物品重量:随机生成n个重量值,范围在[1, V]之间。
2. 算法实现(1)贪心算法:a. 初始化:设置已装载物品重量为0,未装载物品列表;b. 循环:遍历未装载物品列表,选择当前未装载物品中重量与容量比最大的物品;c. 更新:将选择的物品加入已装载物品列表,更新已装载物品重量;d. 判断:若已装载物品重量达到容量限制,结束循环;(2)动态规划:a. 初始化:设置dp[0][0] = 0,其余为-1;b. 遍历:对于每个物品,遍历所有可能的装载方案;c. 更新:根据当前物品的重量和容量,更新dp值;d. 判断:若dp[n][V]不为-1,则找到最优装载方案;(3)遗传算法:a. 初始化:随机生成一定数量的初始种群;b. 适应度函数:根据物品的总重量和容量,计算每个个体的适应度;c. 选择:根据适应度,选择适应度较高的个体进行交叉和变异;d. 交叉和变异:模拟自然选择和遗传变异,生成新的种群;e. 判断:若达到终止条件,输出最优装载方案。
贪心算法实验报告贪心算法实验报告引言:贪心算法是一种常用的算法设计思想,它在求解最优化问题中具有重要的应用价值。
本实验报告旨在介绍贪心算法的基本原理、应用场景以及实验结果,并通过实例加以说明。
一、贪心算法的基本原理贪心算法是一种以局部最优解为基础,逐步构建全局最优解的算法。
其基本原理是在每一步选择中都采取当前状态下最优的选择,而不考虑之后的结果。
贪心算法通常具备以下特点:1. 贪心选择性质:当前状态下的最优选择一定是全局最优解的一部分。
2. 最优子结构性质:问题的最优解可以通过子问题的最优解来构造。
3. 无后效性:当前的选择不会影响以后的选择。
二、贪心算法的应用场景贪心算法适用于一些具有最优子结构性质的问题,例如:1. 路径选择问题:如Dijkstra算法中的最短路径问题,每次选择当前距离最短的节点进行扩展。
2. 区间调度问题:如活动选择问题,每次选择结束时间最早的活动进行安排。
3. 零钱找零问题:给定一些面额不同的硬币,如何用最少的硬币凑出指定的金额。
三、实验设计与实现本次实验选择了一个经典的贪心算法问题——零钱找零问题,旨在验证贪心算法的有效性。
具体实现步骤如下:1. 输入硬币面额和需要凑出的金额。
2. 对硬币面额进行排序,从大到小。
3. 从面额最大的硬币开始,尽可能多地选择该面额的硬币,直到不能再选择为止。
4. 重复步骤3,直到凑出的金额等于需要凑出的金额。
四、实验结果与分析我们通过对不同金额的零钱找零问题进行实验,得到了如下结果:1. 当需要凑出的金额为25元时,贪心算法的结果为1个25元硬币。
2. 当需要凑出的金额为42元时,贪心算法的结果为1个25元硬币、1个10元硬币、1个5元硬币、2个1元硬币。
3. 当需要凑出的金额为63元时,贪心算法的结果为2个25元硬币、1个10元硬币、1个1元硬币。
通过实验结果可以看出,贪心算法在零钱找零问题中取得了较好的效果。
然而,贪心算法并不是适用于所有问题的万能算法,它的有效性取决于问题的特性。
最优装载问题的贪心算法实现姓名:(学号:)一、作业及实验目的通过本实验使学生掌握贪心算法基本要素、步骤及其应用二、作业及实验原理本实验是应用贪心算法用Java 编程语言对给定轮船的载重量和一批集装箱,在装载体积不受限制的情况下,将尽可能多的集装箱装上轮船。
最优装载问题的贪心算法见[1] 的p91-92,Java 编程语言见[2]。
三、 作业及实验内容1. 计算问题及描述:问题描述:给定轮船的载重量c ,第n 个集装箱及其重量w[n],将尽可能多得集装箱装上轮船。
设第i 个集装箱为i w ,最多可放数量n 个。
问题形式为:1max n i i x=∑1n i i i w xc =≤∑ x (0,1),1x i n ∈≤≤2. 算法设计及描述:验证问题是否符合贪心算法:(1)该问题具备贪心选择性质:c 为定值时,i w 越小时,可装载的集装箱数量n 越大。
问题划分为m 个子问题,只要依次选择最小重量集装箱,满足小于等于c 。
原问题即可由n 个子问题的最优解得到整体的最优解。
则最优装在问题具有贪心选择性质。
()1122n n m m y max x w x w x w x w =++⋯++⋯+ 先排序整个集装箱,然后尽可能多地选出前n 个集装箱,要求()1122n n m m y max x w x w x w x w c.=++⋯++⋯+≤ 输出所选集装箱编号。
(2) 该问题具备最优子结构性质:一个问题的最优解包含其子问题的最优解,所以,最优装载问题具有最优子结构性质。
(3) 由于最优装载问题的贪心选择性质和最优子结构性质,最优装载问题符合贪心算法。
3. 算法分析:给出具体的算法复杂度—算法运行时间的渐近表示 排序的时间复杂度为()Onlogn , for 循环的时间复杂度为()o n ;所以空间复杂度为O(m)。
4. 程序设计:根据所设计的算法,写出完整的算法Java 程序或 其他语言程序,并给出相应的程序运行结果算法的程序实现:#include"stdafx.h"void outputResult(int *r,int len){printf("结果:");for(int i=0;i<len;i++){printf("%d\t",r[i])}printf("\n");}void sortBox(int *box,int n){for(int i=n-1;i>0;i--){for(int j=0;j<i;j++){if(box[j]>box[j+1]){int temp=boa[j];box[j]=box[j+1];box[j+1]=temp;}}}}void loading(int *box,int *r,int w,int n){r[0]=1;w=box[0];for(int i=1;i<n;i++){if(w-box[i]>=0){w-=box[i];r[i]=1;}}}int_tmain(int argc,_TCHAR*argv[]){int w=100;int box[6]={100,20,25,25,20,20};sortBox(box,6);int result[6]={0};loading(box,result,w,6);outputResult(result,6);getchar();return 0;}5.实验总结:写出本次作业及实验心得通过本次实验,我们加深领会了贪心算法的中心思想,实验过程中,需要运用了最优子结构性质,贪心选择性质等等,通过对这些知识点得运用,我们更加深层次的了解贪心算法的精髓。
XXXX 大学计算机学院实验报告计算机学院2017级软件工程专业 5 班指导教师
学号姓名2019年10 月28 日成绩
实验内容、上机调试程序、程序运行结果
System.out.print(weight[i]+" ");
}
System.out.println();
//从控制台获取集装箱的最大重量
System.out.println("请输入集装箱的最大重量:");
Scanner s = new Scanner(System.in);
maxWeight=s.nextInt();
System.out.print("可装入的集装箱有:");
//将一批集装箱装上一艘重量为80的轮船。
在装载体积不受限制的情况下,将尽可能多的集装箱装上轮船。
(重量从小到大装)
for(int k=0;k<weight.length;k++){
sumWeight += weight[k];
if(sumWeight<=maxWeight){
System.out.print(weight[k]+"kg ");
}
}
}
}
②完成效果。