算法装载问题

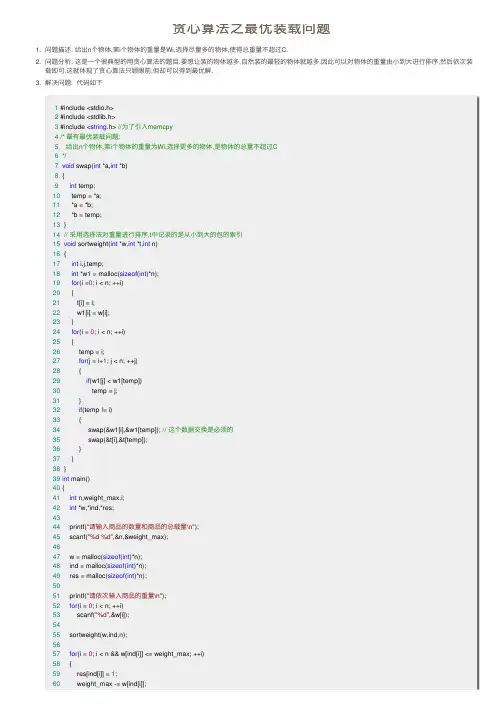
贪⼼算法之最优装载问题1. 问题描述: 给出n个物体,第i个物体的重量是Wi,选择尽量多的物体,使得总重量不超过C.2. 问题分析: 这是⼀个很典型的⽤贪⼼算法的题⽬.要想让装的物体越多,⾃然装的最轻的物体就越多.因此可以对物体的重量由⼩到⼤进⾏排序,然后依次装载即可.这就体现了贪⼼算法只顾眼前,但却可以得到最优解.3. 解决问题: 代码如下4. 1 #include <stdio.h>2 #include <stdlib.h>3 #include <string.h> //为了引⼊memcpy4/* 最有最优装载问题:5给出n个物体,第i个物体的重量为Wi,选择更多的物体,是物体的总量不超过C6*/7void swap(int *a,int *b)8 {9int temp;10 temp = *a;11 *a = *b;12 *b = temp;13 }14// 采⽤选择法对重量进⾏排序,t中记录的是从⼩到⼤的包的索引15void sortweight(int *w,int *t,int n)16 {17int i,j,temp;18int *w1 = malloc(sizeof(int)*n);19for(i =0; i < n; ++i)20 {21 t[i] = i;22 w1[i] = w[i];23 }24for(i = 0; i < n; ++i)25 {26 temp = i;27for(j = i+1; j < n; ++j)28 {29if(w1[j] < w1[temp])30 temp = j;31 }32if(temp != i)33 {34 swap(&w1[i],&w1[temp]); // 这个数据交换是必须的35 swap(&t[i],&t[temp]);36 }37 }38 }39int main()40 {41int n,weight_max,i;42int *w,*ind,*res;4344 printf("请输⼊商品的数量和商品的总载量\n");45 scanf("%d %d",&n,&weight_max);4647 w = malloc(sizeof(int)*n);48 ind = malloc(sizeof(int)*n);49 res = malloc(sizeof(int)*n);5051 printf("请依次输⼊商品的重量\n");52for(i = 0; i < n; ++i)53 scanf("%d",&w[i]);5455 sortweight(w,ind,n);5657for(i = 0; i < n && w[ind[i]] <= weight_max; ++i)58 {59 res[ind[i]] = 1;60 weight_max -= w[ind[i]];61 }62 printf("贪⼼算法求解后的结果是:\n");63for(i = 0; i < n; ++i)64 {65 printf("%d ",res[i]);66 }67 printf("\n");68return0;69 }4. 程序分析: 由于不要改变原始物体重量的值,所以在排序的时候要另外再开辟⼀个数组存储重量.并且另外开辟ind[]存放索引记录装载的顺序.ind[]存放的是重量数组中每个元素在这组数组中⼤⼩的顺序(索引).怎样在排序时记录索引需要在练习排序的时候注意下.。

用分支限界算法解装载问题详解一、实验目的1、理解分支限界法的概念，掌握分支限界法的基本要素。

2、掌握设计分支限界法的一般步骤，针对具体问题，能应用分支限界法求解二、实验内容1、问题描述：有一批共个集装箱要装上2艘载重量分别为C1和C2的轮船，其中集装箱i的重量为Wi，且w1+…+wn<= C1+ C2; 装载问题要求确定是否有一个合理的装载方案可将这个集装箱装上这2艘轮船。

如果有，找出一种装载方案。

2、数据输入：文件输入或键盘输入。

3、要求：1）完成上述问题的队列式分支限界法解决问题，时间为1 次课。

2）独立完成实验及实验报告。

三、实验步骤1、理解方法思想和问题要求。

2、采用编程语言实现题目要求。

3、上机输入和调试自己所写的程序。

4、附程序主要代码：#include <bits/stdc++、h>using namespace std;class MaxHeapQNode{public: MaxHeapQNode*parent; int lchild; int weight; int lev;};structcmp{ bool operator()(MaxHeapQNode *&a, MaxHeapQNode *&b)const { return a->weight < b->weight; }};int n;int c;int bestw;int w[100];int bestx[100];voidInPut(){ scanf("%d %d", &n, &c); for(int i =1; i <= n;++i)scanf("%d", &w[i]);}voidAddAliveNode(priority_queue<MaxHeapQNode *,vector<MaxHeapQNode *>, cmp> &q, MaxHeapQNode *E, int wt, int i, int ch){ MaxHeapQNode *p = new MaxHeapQNode; p->parent = E; p->lchild = ch; p->weight = wt; p->lev = i +1; q、push(p);}voidMaxLoading(){ priority_queue<MaxHeapQNode *,vector<MaxHeapQNode *>, cmp > q; // 大顶堆 //定义剩余重量数组r int r[n +1]; r[n] = 0; for(int j = n-j)r[j] = r[j +1] + w[j +1]; int i =1; MaxHeapQNode *E; int Ew = 0; while(i != n +1){ if(Ew + w[i] <= c){ AddAliveNode(q, E, Ew + w[i] + r[i], i,1); } AddAliveNode(q, E, Ew + r[i], i, 0); //取下一节点 E = q、top(); q、pop(); i = E->lev; Ew = E->weight1]; } bestw = Ew; for(int j = n; j > 0;j){ bestx[j] = E->lchild; E = E->parent; }}void OutPut(){ printf("最优装载量为 %d\n", bestw); printf("装载的物品为 \n"); for(int i =1; i <= n; ++i)if(bestx[i] ==1)printf("%d ", i);}int main(){ InPut(); MaxLoading(); OutPut();}5、实验结果：4、装载问题实验分析：1、将wt<=c和Ew+r>=bestw作为限界判定。

航空货运装载问题算法设计与研究航空货运装载问题算法设计与研究随着全球贸易的不断发展，航空货运业务也得到了迅猛的增长。

在航空货运过程中，货物的装载和排列方式对于提高运输效率至关重要。

航空货运装载问题是一种复杂的组合优化问题，涉及到如何在有限的空间中合理装载和排列各种尺寸、形状和重量的货物。

为了解决航空货运装载问题，研究人员们提出了许多算法和方法，并不断改进和优化。

本文将针对航空货运装载问题，从简到繁、由浅入深地探讨算法设计与研究的相关内容。

一、航空货运装载问题的定义与背景分析航空货运装载问题是指在给定的飞机货舱空间和重量限制条件下，如何优化装载和排列货物，使得运输效率最大化。

该问题可以被抽象为一个组合优化问题，需要通过算法求解。

要解决航空货运装载问题，需要考虑以下因素：1. 航空公司的货舱容量和重量限制：不同型号的飞机具有不同的货舱容量和重量限制，需要根据实际情况进行合理装载。

2. 货物的尺寸、形状和重量：货物的尺寸、形状和重量不同，对于装载的方式和顺序有着不同的要求。

3. 装卸过程中的安全性和稳定性：货物在装卸过程中需要保持安全和稳定，避免损坏和意外情况的发生。

二、航空货运装载问题的求解算法为了求解航空货运装载问题，研究人员们提出了多种算法和方法。

根据问题的复杂度和求解的效果，可以分为以下几种算法。

1. 贪心算法贪心算法是一种简单而有效的算法，它根据每个货物的优先级选择最佳的放置位置。

该算法通过贪心策略，逐步选择最佳装载位置，直到将所有货物装载完毕。

然而，贪心算法可能无法找到最优解，因为它只考虑当前局部最优解。

2. 动态规划算法动态规划算法是解决最优化问题的一种常用方法。

在航空货运装载问题中，可以通过动态规划算法来计算每个装载单元的最优解，并逐步求解整个装载问题。

然而，由于航空货运装载问题的复杂性，动态规划算法的时间复杂度会随着问题规模的增加而增加。

3. 遗传算法遗传算法是一种模拟生物进化过程的优化算法。

遗传算法解决装载问题的例子遗传算法是一种优化算法，它模拟自然选择和遗传机制，寻找最优解决方案。

装载问题是指如何最有效地将多个物体装载到一个限定容积的容器中。

本文将介绍遗传算法如何应用于解决装载问题的例子。

首先，我们需要定义问题的目标函数。

在装载问题中，我们希望最小化剩余容量，即最大化已装载物品的总体积。

因此，我们的目标函数可以定义为：f(x) = - (V - ∑vi)其中，f(x)表示染色体x的适应度，V表示容器的容积，vi表示第i个物品的体积。

接下来，我们需要定义染色体的编码方式。

在装载问题中，一种常用的编码方式是二进制编码。

假设我们有n个物品需要装载，我们可以将染色体编码为长度为n的二进制串，其中1表示对应物品被装载，0表示未被装载。

例如，对于四个物品，染色体0101表示第1和第3个物品被装载，第2和第4个物品未被装载。

然后，我们需要定义遗传算法的操作。

遗传算法通常包括选择、交叉和变异三种基本操作。

在装载问题中，我们可以采用轮盘赌选择操作，即根据染色体适应度进行选择。

交叉操作可以采用单点交叉或多点交叉，用于产生新的染色体。

变异操作可以随机翻转某一位二进制数，用于增加染色体的多样性。

最后，我们可以应用遗传算法进行求解。

假设我们有一个装载容器，其容积为100，同时有n个物品需要装载，每个物品的体积随机分布在[1,20]之间。

我们可以先随机生成一组初始染色体，然后进行遗传算法的迭代过程，直到找到最优解。

通过这样的方法，我们可以在较短的时间内找到最优的装载方案，解决装载问题。

此外，遗传算法还可以应用于其他优化问题的求解，具有广泛的应用前景。

航空货运装载问题算法设计与研究一、引言航空货运业是现代经济中不可或缺的一部分，它承载着跨国贸易、物流运输等重要任务。

但是，航空货运装载问题一直是困扰航空业的一个难题。

如何在有限的装载空间中，合理、高效地装载货物，不仅关系到货物的安全和完整性，还关系到航空公司的运营成本和效益。

对航空货运装载问题进行算法设计与研究具有重大意义。

二、航空货运装载问题的背景和现状1. 航空货运装载问题的背景航空货物装载问题是指如何在给定的飞机货仓内，按照一定的装载规则和限制条件，合理排布和装载各种货物，以达到最优的装载效果。

2. 航空货运装载问题的现状目前，在航空货运业中，一般采用人工经验进行货物的装载，存在装载不均匀、装载效率低下等问题。

虽然国内外已经有许多学者对航空货运装载问题进行了研究，但仍然存在许多难点和挑战。

三、航空货运装载问题的算法设计1. 航空货运装载问题的目标在进行算法设计时，首先需要明确航空货运装载问题的目标。

主要包括最大化装载效率、保证货物的安全性和完整性、降低航空公司的运营成本等。

2. 航空货运装载问题的限制条件在进行算法设计时，需要考虑到各种限制条件，如货仓的实际空间大小、货物的种类和重量、货物的特殊要求等。

3. 航空货运装载问题的算法设计方法针对航空货运装载问题，可以采用启发式算法、遗传算法、禁忌搜索算法等进行设计和优化。

通过模拟货物装载的过程，不断调整和优化装载方案，以达到最优的装载效果。

四、航空货运装载问题的研究进展1. 目前的研究成果国内外许多学者对航空货运装载问题进行了研究，提出了许多有效的算法和方法。

这些研究成果在一定程度上解决了航空货运装载问题中的一些难点和挑战。

2. 待解决的问题和挑战尽管已经取得了一定的成果，但航空货运装载问题仍然存在装载效率不高、计算复杂度大等问题，需要进一步深入研究和探讨。

五、个人观点和总结航空货运装载问题的算法设计与研究，是一个复杂而又具有挑战性的课题。

在未来的研究中，可以结合物流信息技术、智能优化算法等手段，进一步提高货物装载的效率和质量。

算法中的最优装载问题问题描述有n个集装箱要装上1艘载重量分别为c的轮船，其中第i个集装箱的重量为wi。

最优装载问题要求确定在装载体积不受限制的情况下，将尽可能多的集装箱装上轮船，并找出一种装载方案其中@w #集装箱的重量数组@c #货船的最大载重量@n #集装箱的个数@r #未被装载的货物重量@cw #当前货船上的载重@i #搜索树的层数@bestw #最优值@bestx #最优解class Loadingdef initialize(weight,cont)@w,@c,@n=weight,cont,weight.length@r,@cw,@i,@bestw=0,0,0,0@x=Array.new@bestx=Array.newfor j in 0..@n-1@r=@r+@w[j];@bestx[j],@x[j]=0,0endprint \\"集装箱的总重量为 #@r,\\n\\"enddef MaxLoadingwhile truewhile @i<=(@n-1) and (@cw+@w[@i]<@c)@r-=@w[@i]@cw+=@w[@i]@x[@i]=1print \\"在左子树中\\",@x[@i],\\"\\n\\"@i+=1endif @i>@n-1for j in 0..@n-1@bestx[j]=@x[@i]print \'到达叶子节点\',j,\\"\\t @bestx[j]\\",@bestx[j],\\"\\n\\" end@bestw=@cwelse@r-=@w[@i];@x[@i]=0;print \'在右子树中\',@x[@i],\\"\\n\\" @i+=1endwhile @cw+@r<=@bestw@i-=1while @i>=0 and (@x[@i]==0)@r+=@w[@i];@i-=1endif @i==-1 thenprint \\"@bestw:\\",@bestwreturnend@x[@i]=0@cw-=@w[@i]@i+=1endendendendweight=[30,10,10]cont=35s=Loading.new(weight,cont)s.MaxLoading运行的结果如下:集装箱的总重量为 50,在左子树中1在右子树中0在右子树中0到达叶子节点0 @bestx[j]nil到达叶子节点1 @bestx[j]nil到达叶子节点2 @bestx[j]nil@bestw:30>Exit code: 0。

算法——分⽀限界法（装载问题）对⽐回溯法回溯法的求解⽬标是找出解空间中满⾜约束条件的所有解，想必之下，分⽀限界法的求解⽬标则是找出满⾜约束条件的⼀个解，或是满⾜约束条件的解中找出使某⼀⽬标函数值达到极⼤或极⼩的解，即在某种意义下的最优解。

另外还有⼀个⾮常⼤的不同点就是，回溯法以深度优先的⽅式搜索解空间，⽽分⽀界限法则以⼴度优先的⽅式或以最⼩耗费优先的⽅式搜索解空间。

分⽀限界法的搜索策略在当前节点（扩展节点）处，先⽣成其所有的⼉⼦节点（分⽀），然后再从当前的活节点（当前节点的⼦节点）表中选择下⼀个扩展节点。

为了有效地选择下⼀个扩展节点，加速搜索的进程，在每⼀个活节点处，计算⼀个函数值（限界），并根据函数值，从当前活节点表中选择⼀个最有利的节点作为扩展节点，使搜索朝着解空间上有最优解的分⽀推进，以便尽快地找出⼀个最优解。

分⽀限界法解决了⼤量离散最优化的问题。

选择⽅法1.队列式（FIFO）分⽀限界法队列式分⽀限界法将活节点表组织成⼀个队列，并将队列的先进先出原则选取下⼀个节点为当前扩展节点。

2.优先队列式分⽀限界法优先队列式分⽀限界法将活节点表组织成⼀个优先队列，并将优先队列中规定的节点优先级选取优先级最⾼的下⼀个节点成为当前扩展节点。

如果选择这种选择⽅式，往往将数据排成最⼤堆或者最⼩堆来实现。

例⼦：装载问题有⼀批共n个集装箱要装上2艘载重量分别为c1，c2的轮船，其中集装箱i的重量为wi，且要求确定是否有⼀个合理的装载⽅案可将这n个集装箱装上这2艘轮船。

可证明，采⽤如下策略可以得到⼀个最优装载⽅案：先尽可能的将第⼀艘船装满，其次将剩余的集装箱装到第⼆艘船上。

代码如下：//分⽀限界法解装载问题//⼦函数，将当前活节点加⼊队列template<class Type>void EnQueue(Queue<Type> &Q, Type wt, Type &bestw, int i, int n){if(i == n) //可⾏叶结点{if(wt>bestw) bestw = wt ;}else Q.Add(wt) ; //⾮叶结点}//装载问题先尽量将第⼀艘船装满//队列式分⽀限界法，返回最优载重量template<class Type>Type MaxLoading(Type w[],Type c,int n){//初始化数据Queue<Type> Q; //保存活节点的队列Q.Add(-1); //-1的标志是标识分层int i=1; //i表⽰当前扩展节点所在的层数Type Ew=0; //Ew表⽰当前扩展节点的重量Type bestw=0; //bestw表⽰当前最优载重量//搜索⼦集空间树while(true){if(Ew+w[i]<=c) //检查左⼉⼦EnQueue(Q,Ew+w[i],bestw,i,n); //将左⼉⼦添加到队列//将右⼉⼦添加到队列即表⽰不将当前货物装载在第⼀艘船EnQueue(Q,Ew,bestw,i,n);Q.Delete(Ew); //取下⼀个节点为扩展节点并将重量保存在Ewif(Ew==-1) //检查是否到了同层结束{if(Q.IsEmpty()) return bestw; //遍历完毕，返回最优值Q.Add(-1); //添加分层标志Q.Delete(Ew); //删除分层标志，进⼊下⼀层i++;}}}算法MaxLoading的计算时间和空间复杂度为O(2^n).上述算法可以改进，设r为剩余集装箱的重量，当Ew+r<=bestw的时候，可以将右⼦树剪去。

贪⼼算法之最优装载问题贪⼼算法之最优装载问题1. 问题描述有⼀批集装箱要装上⼀艘重量为c的轮船，其中集装箱i的重量为W i。

最优装载问题要求确定在装载体积不受限制的情况下，将尽可能多的集装箱装上轮船。

2. 问题分析2.1确定贪⼼策略采⽤重量最轻者先装的贪⼼选择策略，可产⽣该问题的最优解。

2.2代码求解/*** x[] 保存最优解路径数组* w[] 集装箱重量数组* c 船的载重量* n 集装箱的数量**/void Loading(int x[], int w[], int c, int n) {// 按照集装箱重量从⼩到⼤排序sort(w, n);for (int i = 1; i <= n; i++)x[i] = 0;for (int i = 1; i <= n && w[i] <= c; i++) {x[i] = 1;c -= w[i];}}2.3贪⼼选择性质设集装箱依其重量从⼩到⼤排序，(x1,x2,…,x n)是其最优解，x i={0,1}，设x k是第⼀个等于1的。

(1) 如k=1，则满⾜贪⼼选择性质(2) 如k≠1，⽤x1替换x k，构造的新解同原解最优值相同，故也是最优解，满⾜贪⼼选择性质该证明⽅法只证明了任何⼀个最优解都可以转换为第⼀个集装箱上船的最优解（满⾜贪⼼策略）。

此⽅法对⼦问题同样有效，因此可以将⼀个普通最优解转化为满⾜贪⼼策略的最优解。

如(0101)⇒(1100)2.4.最优⼦结构性质最优装载问题具有最优⼦结构性质，设1⾄n个集装箱装上船的最⼤数量为T(1,n,w)，则T(1,n,w)=1+T(2,n,w−w1)；因T(1,n,w)是最优值，则T(2,n,w−w i)⼀定是最优值，反证法证明之反证法：如果T(2,n,w−w1)不是该问题的最优解，则存在最优值T′(2,n,w−w1)>T(2,n,w−w1)，则1+T′(2,n,w−w1)=T′(1,n,w)>T(1,n,w)，这与⼤前提T(1,n,w)是最优值相⽭盾，故T(2,n,w−w1)⼀定是最优值。

算法分析与设计2016/2017(2)实验题目装载问题5种解法学生学生学号学生班级任课教师提交日期2017计算机科学与技术学目录一问题定义 (3)二解决方案 (3)1优先队列式分支限界法求解 (3)1.1算法分析 (3)1.2代码 (3)1.3运行结果 (13)2队列式分支限界法求解 (13)2.1算法分析 (13)2.2代码 (14)2.3测试截图 (22)3回朔法-迭代 (22)3.1算法分析 (22)3.2代码 (22)3.3测试截图 (26)4回朔法-递归 (26)4.1算法分析 (26)4.2代码 (27)4.3测试截图 (31)5贪心算法 (31)5.1算法分析 (31)5.2代码 (31)5.3测试截图 (35)一问题定义有一批共有 n 个集装箱要装上两艘载重量分别为 c1 和 c2 的轮船，其中集装箱 i 的重量为 w[i], 且重量之和小于(c1 + c2)。

装载问题要求确定是否存在一个合理的装载方案可将这 n 个集装箱装上这两艘轮船。

如果有，找出一种装载方案。

二解决方案1优先队列式分支限界法求解1.1算法分析活结点x在优先队列中的优先级定义为从根结点到结点x的路径所相应的载重量再加上剩余集装箱的重量之和。

优先队列中优先级最大的活结点成为下一个扩展结点。

以结点x为根的子树中所有结点相应的路径的载重量不超过它的优先级。

子集树中叶结点所相应的载重量与其优先级相同。

在优先队列式分支限界法中，一旦有一个叶结点成为当前扩展结点，则可以断言该叶结点所相应的解即为最优解。

此时可终止算法。

1.2代码1.2-1////MaxHeap.htemplate<class T>class MaxHeap{public:MaxHeap(int MaxHeapSize = 10);~MaxHeap() {delete [] heap;}int Size() const {return CurrentSize;}T Max(){ //查找if (CurrentSize == 0){throw OutOfBounds();}return heap[1];}MaxHeap<T>& Insert(const T& x); //增MaxHeap<T>& DeleteMax(T& x); //删void Initialize(T a[], int size, int ArraySize);private:int CurrentSize, MaxSize;T *heap; // element array};template<class T>MaxHeap<T>::MaxHeap(int MaxHeapSize){// Max heap constructor.MaxSize = MaxHeapSize;heap = new T[MaxSize+1];CurrentSize = 0;}template<class T>MaxHeap<T>& MaxHeap<T>::Insert(const T& x){// Insert x into the max heap.if (CurrentSize == MaxSize){cout<<"no space!"<<endl;return *this;}// 寻找新元素x的位置// i——初始为新叶节点的位置，逐层向上，寻找最终位置int i = ++CurrentSize;while (i != 1 && x > heap[i/2]){// i不是根节点，且其值大于父节点的值，需要继续调整heap[i] = heap[i/2]; // 父节点下降i /= 2; // 继续向上，搜寻正确位置}heap[i] = x;return *this;}template<class T>MaxHeap<T>& MaxHeap<T>::DeleteMax(T& x){// Set x to max element and delete max element from heap.// check if heap is emptyif (CurrentSize == 0){cout<<"Empty heap!"<<endl;return *this;}x = heap[1]; // 删除最大元素// 重整堆T y = heap[CurrentSize--]; // 取最后一个节点，从根开始重整// find place for y starting at rootint i = 1, // current node of heapci = 2; // child of iwhile (ci <= CurrentSize){// 使ci指向i的两个孩子中较大者if (ci < CurrentSize && heap[ci] < heap[ci+1]){ci++;}// y的值大于等于孩子节点吗？if (y >= heap[ci]){break; // 是，i就是y的正确位置，退出}// 否，需要继续向下，重整堆heap[i] = heap[ci]; // 大于父节点的孩子节点上升i = ci; // 向下一层，继续搜索正确位置ci *= 2;}heap[i] = y;return *this;}template<class T>void MaxHeap<T>::Initialize(T a[], int size,int ArraySize){// Initialize max heap to array a.delete [] heap;heap = a;CurrentSize = size;MaxSize = ArraySize;// 从最后一个部节点开始，一直到根，对每个子树进行堆重整for (int i = CurrentSize/2; i >= 1; i--){T y = heap[i]; // 子树根节点元素// find place to put yint c = 2*i; // parent of c is target// location for ywhile (c <= CurrentSize){// heap[c] should be larger siblingif (c < CurrentSize && heap[c] < heap[c+1]){c++;}// can we put y in heap[c/2]?if (y >= heap[c]){break; // yes}// noheap[c/2] = heap[c]; // move child upc *= 2; // move down a level}heap[c/2] = y;}}1.2-2///6d3-2.cpp//装载问题优先队列式分支限界法求解#include "stdafx.h"#include "MaxHeap.h"#include <iostream>using namespace std;const int N = 4;class bbnode;template<class Type>class HeapNode{template<class Type>friend void AddLiveNode(MaxHeap<HeapNode<Type>>& H,bbnode *E,Type wt,bool ch,int lev);template<class Type>friend Type MaxLoading(Type w[],Type c,int n,int bestx[]);public:operator Type() const{return uweight;}private:bbnode *ptr; //指向活节点在子集树中相应节点的指针Type uweight; //活节点优先级(上界)int level; //活节点在子集树中所处的层序号};class bbnode{template<class Type>friend void AddLiveNode(MaxHeap<HeapNode<Type>>& H,bbnode *E,Type wt,bool ch,int lev);template<class Type>friend Type MaxLoading(Type w[],Type c,int n,int bestx[]);friend class AdjacencyGraph;private:bbnode *parent; //指向父节点的指针bool LChild; //左儿子节点标识};template<class Type>void AddLiveNode(MaxHeap<HeapNode<Type>>& H,bbnode *E,Type wt,bool ch,int lev);template<class Type>Type MaxLoading(Type w[],Type c,int n,int bestx[]);int main(){float c = 70;float w[] = {0,20,10,26,15};//下标从1开始int x[N+1];float bestw;cout<<"轮船载重为："<<c<<endl;cout<<"待装物品的重量分别为："<<endl;for(int i=1; i<=N; i++){cout<<w[i]<<" ";}cout<<endl;bestw = MaxLoading(w,c,N,x);cout<<"分支限界选择结果为:"<<endl;for(int i=1; i<=4; i++){cout<<x[i]<<" ";}cout<<endl;cout<<"最优装载重量为："<<bestw<<endl;return 0;}//将活节点加入到表示活节点优先队列的最大堆H中template<class Type>void AddLiveNode(MaxHeap<HeapNode<Type>>& H,bbnode *E,Type wt,bool ch,intlev){bbnode *b = new bbnode;b->parent = E;b->LChild = ch;HeapNode<Type> N;N.uweight = wt;N.level = lev;N.ptr = b;H.Insert(N);}//优先队列式分支限界法，返回最优载重量，bestx返回最优解template<class Type>Type MaxLoading(Type w[],Type c,int n,int bestx[]) {//定义最大的容量为1000MaxHeap<HeapNode<Type>> H(1000);//定义剩余容量数组Type *r = new Type[n+1];r[n] = 0;for(int j=n-1; j>0; j--){r[j] = r[j+1] + w[j+1];}//初始化int i = 1;//当前扩展节点所处的层bbnode *E = 0;//当前扩展节点Type Ew = 0; //扩展节点所相应的载重量//搜索子集空间树while(i!=n+1)//非叶子节点{//检查当前扩展节点的儿子节点if(Ew+w[i]<=c){AddLiveNode(H,E,Ew+w[i]+r[i],true,i+1);}//右儿子节点AddLiveNode(H,E,Ew+r[i],false,i+1);//取下一扩展节点HeapNode<Type> N;H.DeleteMax(N);//非空i = N.level;E = N.ptr;Ew = N.uweight - r[i-1];}//构造当前最优解for(int j=n; j>0; j--){bestx[j] = E->LChild;E = E->parent;}return Ew;}1.3运行结果2队列式分支限界法求解2.1算法分析在算法的循环体中，首先检测当前扩展结点的左儿子结点是否为可行结点。

实验六 回溯算法〔2学时〕一、实验目的与要求1、掌握装载问题的回溯算法；2、初步掌握回溯算法；二、实验题有一批共n 个集装箱要装上2艘载重量分别为c1和c2的轮船，其中集装箱i 的重量为wi ，且 装载问题要求确定是否有一个合理的装载方案可将这个集装箱装上这2艘轮船。

如果有，找出一种装载方案。

三、实验提示void backtrack (int i){// 搜索第i 层结点if (i > n) // 到达叶结点更新最优解bestx,bestw;return;r -= w[i];if (cw + w[i] <= c) {// 搜索左子树x[i] = 1;cw += w[i];backtrack (i + 1);cw -= w[i]; }if (cw + r > bestw) {x[i] = 0; // 搜索右子树backtrack (i + 1); }r += w[i];}四、实验代码方法1：import java.util.*;/*** 回溯法解决装载问题* author Administrator**/public class demo {public static int n; //集装箱数public static int first_weight; //第一艘载重量public static int beautif_weight; //当前最优载重量public static int[] arr_weight; //集装箱重量数组public static int[] **; //public static int[] best**;public static int maxLoadingRE(int[] w, int c, int[] bestx) {//递归回溯 n = w.length;first_weight = c;beautif_weight = 0;211c c w n i i +≤∑=arr_weight = w;best** = bestx;** = new int[n];int r = 0; //剩余集装箱重量，未进展装载的重量for (int i = 0; i < n; i++) {r += arr_weight[i];}trackback(0, 0, r);return beautif_weight;}//到达层数，目前装载的重量，未装载的重量private static void trackback(int i, int cw, int r) {if (i == n) {//到达叶结点for (int j = 0; j < n; j++) {best**[j] = **[j];}beautif_weight = cw;return; //只是一次出栈操作，栈非空还要继续执行}if (cw + arr_weight[i] <= first_weight) { //已装载的加上要装载的小于第一个的载重量**[i] = 0; //0代表装在第一个上，1代表装在第二个上trackback(i + 1, cw + arr_weight[i], r); //试图装载下一个集装箱，r是针对第一个装的重量，因此装在第一个里不需要减，但装在第二个时就要减去该重量}if (r - arr_weight[i] > beautif_weight) { //已装载的加上要装载的已经大于第一个的载重量，并且用总的载重量r减去当前要装载的还比最好的载重量大**[i] = 1; //放到第二个上trackback(i + 1, cw, r - arr_weight[i]);}}public static int maxLoading(int[] w, int c, int[] bestx) {int i = 0; //当前层int n = w.length; //层总数int[] x = new int[n]; //x[0, i]为当前选择路径Arrays.fill(x, -1); //初始化为-1，0表示选择第一个，1表示选择第二个int bestw = 0; //当前最优装载重量int[] cw = new int[n]; //当前载重量int[] r = new int[n]; //剩余集装箱容量int tor = 0;for (int item : w) {//item取出w中的值，进展相加tor += item;}r[0] = tor;//要装载的重量cw[0] = 0;//搜索子树while (i > -1) {do {x[i] += 1;if (x[i] == 0) { //选择放在第一个〔左子树〕if (cw[i] + w[i] <= c) {if (i < n - 1) {cw[i + 1] = cw[i] + w[i];r[i + 1] = r[i];}break; //能放下就直接跳出这个do-while循环}}else { //选择放在第二个〔右子树〕if (r[i] - w[i] > bestw) {//剪枝函数，没有最优解好的话x[i]会自增到2，不会进入下面的if (x[i] < 2)if (i < n - 1) {r[i + 1] = r[i] - w[i];cw[i + 1] = cw[i];}break;}}} while (x[i] < 2); //对于放不下的在这里判断后才能取右子树if (x[i] < 2) {if (i == n - 1) {for (int j = 0; j < n; j++) {bestx[j] = x[j];}if (x[i] == 0) {bestw = cw[i] + w[i];}else {bestw = cw[i];}}else {i++;x[i] = -1;}}else {//当x[i]=2时，说明已经遍历完两个叶节点，应向上一层继续遍历其它节点i--;}}return bestw;}public static void main(String[] args) {int[] w = {0,10,40,40};int n = w.length;int c = 50;int[] bestx = new int[n];System.out.println("重量分别为：");for(int ws:w){System.out.print(","+ws);}System.out.println("\n");int bestw = maxLoadingRE(w, c, bestx);System.out.println("回溯选择结果为: " + bestw); System.out.println(Arrays.toString(bestx));}}方法2：public class demo2 {public static void main(String[] args) {int n=3,m;int c=50,c2=50;int w[]={0,10,40,40};int bestx[]=new int[w.length];demo2 demo2=new demo2();m=demo2.MaxLoading(w, c, n, bestx);System.out.println("轮船的载重量分别为：");System.out.println("c(1)="+c+",c(2)="+c2);System.out.println("待装集装箱重量分别为：");System.out.print("w(i)=");for (int i=0;i<=n;i++){System.out.print("，"+w[i]);}System.out.println(");System.out.println("最优装载量为：");System.out.println("m(1)="+m);System.out.print("x(i)=");for (int i=0;i<=n;i++){System.out.print("+bestx[i]);}System.out.println(");int m2=0;for (int j=1;j<=n;j++){m2=m2+w[j]*(1-bestx[j]);}System.out.println("回溯选择结果为:"+m2);if(m2>c2){System.out.println("因为m(2)大于c(2),所以原问题无解！");}}int MaxLoading(int w[],int c,int n,int bestx[])//迭代回溯法，返回最优载重量及其相应解，初始化根结点{int i=1;//当前层，x[1:i-1]为当前路径int x[]=new int[n+1];int bestw=0; //当前最优载重量int cw=0; //当前载重量int r=0; //剩余集装箱重量for (int j=1;j<=n;j++){r+=w[j];}while(true)//搜索子树{while(i<=n &&cw+w[i]<=c)//进入左子树{r-=w[i];cw+=w[i];x[i]=1;i++;}if (i>n)//到达叶结点{for (int j=1;j<=n;j++){bestx[j]=x[j];}bestw=cw;}else//进入右子树{r-=w[i];x[i]=0; i++;}while (cw+r<=bestw){ //剪枝回溯i--;while (i>0){r+=w[i];i--;}//从右子树返回if (i==0){return bestw;}x[i]=0;cw-=w[i];i++;}}}}五、实验结果六、实验总结。

在优先队列式分支限界法中，一旦有一叶结点成为当前的扩展结点，则可以 断言该叶结点所相应的解即为最优解。此时可终止算法。
x谢谢~
解装载问题的优先队列式分支限界法用最大优先队列存储活结点表。活结点 x在优先队列中的优先级定义为从根结点到结点x的路径所相应的载重量再加 上剩余集装箱的重量之和。
优先队列中优先级最大的活结点成为下一个扩展结点。以节点x为根的子树 中所有结点相应的路径的载重量不超过它的优先级。子集树中叶节点所相应 的载重量与其优先级相同。
➢ class QNode ➢{ ➢ QNode *parent;//指向父节点的指
针 ➢ bool LChild;//左儿子标志 ➢ Type weight;//结点所相应的载重量 ➢}
➢ //构造当前最优解 ➢ for(int j=n-1;j>0;j--) ➢{ ➢ bestx[j]=bestE->Lchild; ➢ bestE=bestE->parent; ➢}
➢ 在算法的while循环中，首先检测当 Whi{
行节点。如果是，则将其加入到活 //检查左儿子结点
结点队列中，然后将其右儿子节点 if(Ew+w[i] <=c)//x[i]=1
加入到活结点队列中（右儿子结点
EnQueue(Q,Ew+w[i],bestw,i,n);
max wi xi i 1
n
s.t.
wi xi c1
i 1
xi {0,1},1 i n
装载问题实质上是求第一艘船的最优装载
该算法只求出所要求的最优值。算法 MaxLoading实施对解空间的分支限界搜索。 队列Q用于存放活结点表，其中元素的值表 示活结点所相应的当前载重量。当元素值为1时，表示队列已到达解空间树同一层节点 的尾部。

算法学习——动态规划之装载问题算法描述两艘船各⾃可装载重量为c1，c2，n个集装箱，各⾃的重量为w[n]，设计⼀个可以装载的⽅案，使得两艘船装下全部集装箱算法思路将第⼀艘船尽量装满（第⼀艘船放的集装箱的重量之和接近c1），剩余的集装箱放⼊第⼆艘船，若剩余的集装箱重量之和⼤于第⼆艘船，则⽆解定义⼀个⼀维数组，a[n] 存放对应的集装箱的重量定义⼀个数组，m[i][j]表⽰第⼀艘船还可装载的重量j，可取集装箱编号范围为i，i+1...n的最⼤装载重量值例如现在有3个集装箱重量分别为9，5，3,即a[1]=9 a[2]=5 a[3]=3m[1][2]=0 可装载重量为2，此时上述的三个集装箱都不能装⼊，所以为最⼤可装载重量为0m[1][3]=m[1][4]=3 可装载重量为3或者是4的时候，都是只能装⼊重量为3的那个集装箱，所以最⼤可装载重量为3 `实际上，这⾥的3=a[3]+m[1][2]，是⼀个递推的关系，具体看下⾯`m[i][j]分下⾯两种情况0<=j<a[n] (当可装载重量j⼩于第n个集装箱的重量w[n]，此时就不能往船上装此集装箱) m[i][j] = m[i+1][j]j>=a[n] （可装载重量j⼤于或等于第n个集装箱的重量w[n]）,此时剩余的可装载重量为j-a[n](装⼊了此时的集装箱)，最⼤的可装载重量为m[i+1][j-w[n]]+w[n]但是我们是需要最⼤的可装载重量，所以得与如果不将当前集装箱装⼊的那种情况m[i+1][j]进⾏⽐较m[i][j]=Math.max(m[i+1][j],m[i+1][j-a[n]+a[n]])上⾯我们就获得了⼀个关于m[i][j]的递推关系，我们通过逆推获得全部的数值初始值m[i][j]=0 这⾥的i=n j从0到a[n] 这⾥的a[n]是第n个集装箱重量（最后⼀个集装箱的重量）这⾥的赋值其实就是上述m[i][j]两种情况的第⼀种情况，最后⼀个集装箱的重量⼤于可装载重量，不装载此集装箱，所以最⼤可装载重量为0，m[i][j]=a[n] 这⾥的i=n j从a[n]到c1 这⾥的a[n]是第n个集装箱的重量（最后⼀个集装箱的重量）这⾥的意思为当可装载重量j只要都是⼤于最后⼀个集装箱的重量a[n]，即可装⼊此集装箱，所以最⼤可装载重量等于装⼊的集装箱的重量开始逆推使⽤上述的递推公式进⾏逆推for (int i = n; i >= 1 ; i--) {for (int j = 1; j <=c1; j++) {if(j>=a[i]){m[i][j] = Math.max(m[i+1][j],m[i+1][j-a[i]]+a[i]);}else{m[i][j]=m[i+1][j];}}}之后再进⾏输出，输出第⼀艘船的装载⽅案，输出第⼆艘船的装载⽅案算法实现System.out.println("输⼊第⼀艘船可装载重量c1:");Scanner scanner = new Scanner(System.in);int c1 = scanner.nextInt();System.out.println("输⼊第⼆艘船可装载重量c2：");int c2 = scanner.nextInt();System.out.println("输⼊集装箱个数n：");int n = scanner.nextInt();int[] a = new int[n+1];//使⽤⼀维数组存放集装箱重量System.out.println("依次输⼊集装箱的重量");for (int i =1; i < n+1; i++) {a[i] = scanner.nextInt();}int sum = 0;//集装箱重量总和for (int i = 0; i < a.length; i++) {sum=sum+a[i];}//超重情况if(sum>c1+c2){System.out.println("集装箱重量之和⼤于两艘船可装载重量，题⽬⽆解");return;//结束程序}int[][] m = new int[100][100];//m[i][j]表⽰第⼀艘船还可装载的重量j，可取集装箱编号范围为i，i+1...n的最⼤装载重量值 //赋初始值,由于是逆推，所以从末尾开始//可装载重量j⼩于第n个集装箱重量a[n]，不装此集装箱，赋值为0for (int j = 0; j < a[n]; j++) {m[n][j] = 0;}//可装载重量j⼤于或等于第n个集装箱重量a[n]，装载此集装箱，此时刻最⼤装载重量值为a[n]for (int j = a[n]; j <=c1 ; j++) {m[n][j]=a[n];}//关键逆推代码for (int i = n; i >= 1 ; i--) {for (int j = 1; j <=c1; j++) {if(j>=a[i]){m[i][j] = Math.max(m[i+1][j],m[i+1][j-a[i]]+a[i]);}else{m[i][j]=m[i+1][j];}}}int maxc1 = m[1][c1];//最⼤可装载重量System.out.println("maxc1="+maxc1);if(maxc1>sum-c2){int cw = m[1][maxc1];int sw,i;//输出第⼀艘船的装载System.out.println("第⼀艘船装载：");for (sw=0,i=1;i<=n;i++){if(m[i][cw]>m[i+1][cw]){cw = cw-a[i];sw=sw+a[i];//统计sw，sw的最终结果与maxc1相等System.out.print(a[i]+" ");a[i]=0;//装载当前的集装箱}}System.out.print("("+sw+")");System.out.println("");//输出第⼆艘船的装载System.out.println("第⼆艘船装载：");for(sw=0,i=1;i<=n;i++){//已装载在第⼀艘船的集装箱a[i]都已经为0了,只需要将不为0的那些集装箱装⼊第⼆艘船即可if(a[i]!=0){System.out.print(a[i]+" ");sw=a[i]+sw;}}System.out.println("("+sw+")"); }else{System.out.println("⽆解"); }结果。

一、实验背景算法装载问题（Bin Packing Problem）是组合优化领域中的一个经典问题，主要研究如何将一组物品装入有限数量的容器中，使得容器中的物品总重量不超过容器的容量，同时尽可能减少容器的数量。

该问题在实际应用中具有广泛的意义，如物流运输、资源分配、生产计划等领域。

二、实验目的1. 了解算法装载问题的基本概念和特点；2. 掌握几种常用的算法装载问题的解决方法；3. 通过实验验证不同算法在解决算法装载问题时的性能；4. 分析算法的优缺点，为实际应用提供参考。

三、实验内容1. 实验环境操作系统：Windows 10编程语言：Python 3.8实验工具：Pandas、Numpy、Scipy2. 实验方法（1）遗传算法遗传算法是一种模拟自然选择和遗传学原理的搜索启发式算法。

在算法装载问题中，可以将物品和容器看作基因，通过交叉、变异等操作，不断优化解的质量。

（2）贪心算法贪心算法是一种在每一步选择中都采取当前最优策略的算法。

在算法装载问题中，可以根据物品的重量或容器的容量，对物品进行排序，然后依次将物品装入容器。

（3）动态规划动态规划是一种将复杂问题分解为子问题，并存储子问题的解的方法。

在算法装载问题中，可以根据物品的重量和容器的容量，计算最优解。

3. 实验数据实验数据来源于一组具有不同重量和数量的物品，以及不同容量和数量的容器。

四、实验结果与分析1. 遗传算法实验结果表明，遗传算法在解决算法装载问题时具有较高的求解能力。

随着迭代次数的增加，解的质量逐渐提高，但求解时间较长。

2. 贪心算法贪心算法在解决算法装载问题时具有较快的求解速度，但解的质量相对较差。

在部分情况下，贪心算法得到的解甚至无法满足所有容器的容量要求。

3. 动态规划动态规划在解决算法装载问题时具有较高的求解质量，但求解时间较长。

对于大型问题，动态规划可能无法在合理时间内得到最优解。

五、结论通过对遗传算法、贪心算法和动态规划在算法装载问题中的应用实验，得出以下结论：1. 遗传算法具有较高的求解能力，但求解时间较长；2. 贪心算法求解速度快，但解的质量较差；3. 动态规划求解质量高，但求解时间较长。

0034算法笔记——【分⽀限界法】最优装载问题问题描述有⼀批共个集装箱要装上2艘载重量分别为C1和C2的轮船，其中集装箱i的重量为Wi，且装载问题要求确定是否有⼀个合理的装载⽅案可将这个集装箱装上这2艘轮船。

如果有，找出⼀种装载⽅案。

容易证明：如果⼀个给定装载问题有解，则采⽤下⾯的策略可得到最优装载⽅案。

(1)⾸先将第⼀艘轮船尽可能装满；(2)将剩余的集装箱装上第⼆艘轮船。

1、队列式分⽀限界法求解在算法的循环体中，⾸先检测当前扩展结点的左⼉⼦结点是否为可⾏结点。

如果是则将其加⼊到活结点队列中。

然后将其右⼉⼦结点加⼊到活结点队列中(右⼉⼦结点⼀定是可⾏结点)。

2个⼉⼦结点都产⽣后，当前扩展结点被舍弃。

活结点队列中的队⾸元素被取出作为当前扩展结点，由于队列中每⼀层结点之后都有⼀个尾部标记-1，故在取队⾸元素时，活结点队列⼀定不空。

当取出的元素是-1时，再判断当前队列是否为空。

如果队列⾮空，则将尾部标记-1加⼊活结点队列，算法开始处理下⼀层的活结点。

节点的左⼦树表⽰将此集装箱装上船，右⼦树表⽰不将此集装箱装上船。

设bestw是当前最优解；ew是当前扩展结点所相应的重量；r是剩余集装箱的重量。

则当ew+r为了在算法结束后能⽅便地构造出与最优值相应的最优解，算法必须存储相应⼦集树中从活结点到根结点的路径。

为此⽬的，可在每个结点处设置指向其⽗结点的指针，并设置左、右⼉⼦标志。

找到最优值后，可以根据parent回溯到根节点，找到最优解。

算法具体代码实现如下：1、Queue.h[cpp]view plain copy1.#include/doc/951702836.htmling namespace std;3.4.template5.class Queue6.{7.public:8. Queue(int MaxQueueSize=50);9. ~Queue(){delete [] queue;}10.bool IsEmpty()const{return front==rear;}11.bool IsFull(){return ( ( (rear+1) %MaxSize==front )?1:0);}12. T Top() const;13. T Last() const;14. Queue& Add(const T& x);15. Queue& AddLeft(const T& x);16. Queue& Delete(T &x);17.void Output(ostream& out)const;18.int Length(){return (rear-front);}19.private:20.int front;21.int rear;22.int MaxSize;23. T *queue;24.};25.26.template27.Queue::Queue(int MaxQueueSize)28.{29. MaxSize=MaxQueueSize+1;30. queue=new T[MaxSize];31. front=rear=0;32.}33.34.template35.T Queue::Top()const36.{37.if(IsEmpty())38. {39. cout<<"queue:no element,no!"<40.return 0;41. }42.else return queue[(front+1) % MaxSize];43.}44.45.template46.T Queue ::Last()const47.{48.if(IsEmpty())49. {50. cout<<"queue:no element"<51.return 0;52. }53.else return queue[rear];54.}55.56.template57.Queue& Queue::Add(const T& x)58.{59.if(IsFull())cout<<"queue:no memory"<60.else61. {62. rear=(rear+1)% MaxSize;63. queue[rear]=x;64. }65.return *this;66.}67.68.template69.Queue& Queue::AddLeft(const T& x)70.{71.if(IsFull())cout<<"queue:no memory"<72.else73. {74. front=(front+MaxSize-1)% MaxSize;75. queue[(front+1)% MaxSize]=x;76. }77.return *this;78.}79.80.template81.Queue& Queue ::Delete(T & x)82.{83.if(IsEmpty())cout<<"queue:no element(delete)"<84.else85. {86. front=(front+1) % MaxSize;87. x=queue[front];88. }89.return *this;90.}91.92.93.template94.void Queue ::Output(ostream& out)const95.{96.for(int i=rear%MaxSize;i>=(front+1)%MaxSize;i--)97. out<98.}99.100.template101.ostream& operator << (ostream& out,const Queue& x) 102.{x.Output(out);return out;} 2、6d3-1.cpp[cpp]view plain copy1.//装载问题队列式分⽀限界法求解2.#include "stdafx.h"3.#include "Queue.h"4.#include/doc/951702836.htmling namespace std;6.7.const int N = 4;8.9.template10.class QNode11.{12.template13.friend void EnQueue(Queue*>&Q,Type wt,int i,int n,Type bestw,QNode*E,QNode *&bestE,int bestx[],bool ch);14.15.template16.friend Type MaxLoading(Type w[],Type c,int n,int bestx[]);17.18.private:19. QNode *parent; //指向⽗节点的指针20.bool LChild; //左⼉⼦标识21. Type weight; //节点所相应的载重量22.};23.24.template25.void EnQueue(Queue*>&Q,Type wt,int i,int n,Type bestw,QNode >*E,QNode *&bestE,int bestx[],bool ch);26.27.template28.Type MaxLoading(Type w[],Type c,int n,int bestx[]);29.30.int main()31.{32.float c = 70;33.float w[] = {0,20,10,26,15};//下标从1开始34.int x[N+1];35.float bestw;36.37. cout<<"轮船载重为："<38. cout<<"待装物品的重量分别为："<39.for(int i=1; i<=N; i++)40. {41. cout<42. }43. cout<44. bestw = MaxLoading(w,c,N,x);45.46. cout<<"分⽀限界选择结果为:"<47.for(int i=1; i<=4; i++)48. {49. cout<50. }51. cout<52. cout<<"最优装载重量为："<53.54.return 0;55.}56.57.//将活节点加⼊到活节点队列Q中58.template59.void EnQueue(Queue*>&Q,Type wt,int i,int n,Type bestw,QNode >*E,QNode *&bestE,int bestx[],bool ch)60.{61.if(i == n)//可⾏叶节点62. {63.if(wt == bestw)64. {65.//当前最优装载重量66. bestE = E;67. bestx[n] = ch;68. }69.return;70. }71.//⾮叶节点72. QNode *b;73. b = new QNode;74. b->weight = wt;75. b->parent = E;76. b->LChild = ch;77. Q.Add(b);78.}79.80.template81.Type MaxLoading(Type w[],Type c,int n,int bestx[])82.{//队列式分⽀限界法，返回最优装载重量，bestx返回最优解83.//初始化84. Queue*> Q; //活节点队列85. Q.Add(0); //同层节点尾部标识86.int i = 1; //当前扩展节点所处的层87. Type Ew = 0, //扩展节点所相应的载重量88. bestw = 0, //当前最优装载重量89. r = 0; //剩余集装箱重量90.91.for(int j=2; j<=n; j++)92. {93. r += w[j];94. }95.96. QNode *E = 0, //当前扩展节点97. *bestE; //当前最优扩展节点98.99.//搜索⼦集空间树100.while(true)101. {102.//检查左⼉⼦节点103. Type wt = Ew + w[i];104.if(wt <= c)//可⾏节点105. {106.if(wt>bestw)107. {108. bestw = wt;109. }110. EnQueue(Q,wt,i,n,bestw,E,bestE,bestx,true); 111. } 112.113.//检查右⼉⼦节点114.if(Ew+r>bestw)115. {116. EnQueue(Q,Ew,i,n,bestw,E,bestE,bestx,false); 117. } 118. Q.Delete(E);//取下⼀扩展节点119.120.if(!E)//同层节点尾部121. {122.if(Q.IsEmpty())123. {124.break;125. }126. Q.Add(0); //同层节点尾部标识127. Q.Delete(E); //取下⼀扩展节点128. i++; //进⼊下⼀层129. r-=w[i]; //剩余集装箱重量130. }131. Ew =E->weight; //新扩展节点所对应的载重量132. }133.134.//构造当前最优解135.for(int j=n-1; j>0; j--)136. {137. bestx[j] = bestE->LChild;138. bestE = bestE->parent;139. }140.return bestw;141.}程序运⾏结果如图：2、优先队列式分⽀限界法求解解装载问题的优先队列式分⽀限界法⽤最⼤优先队列存储活结点表。

贪⼼算法-装载问题贪⼼选择算法为算法分析中⼀种常⽤算法，通过⼀系列的选择来得到⼀个问题的解。

它所作的每⼀个选择都是当前状态下某种意义的最好选择，即贪⼼选择。

希望通过每次所作的贪⼼选择导致最终结果是问题的⼀个最优解。

这种启发式的策略并不总能奏效，然⽽在许多情况下确能达到预期的⽬的。

对于可利⽤贪⼼算法解决的问题需要同时满⾜：最优⼦结构性质和贪⼼选择性质。

1．贪⼼选择性质所谓贪⼼选择性质是指所求问题的整体最优解可以通过⼀系列局部最优的选择，即贪⼼选择来达到。

这是贪⼼算法可⾏的第⼀个基本要素，也是贪⼼算法与动态规划算法的主要区别。

在动态规划算法中，每步所作的选择往往依赖于相关⼦问题的解。

因⽽只有在解出相关⼦问题后，才能作出选择。

⽽在贪⼼算法中，仅在当前状态下作出最好选择，即局部最优选择。

然后再去解作出这个选择后产⽣的相应的⼦问题。

贪⼼算法所作的贪⼼选择可以依赖于以往所作过的选择，但决不依赖于将来所作的选择，也不依赖于⼦问题的解。

正是由于这种差别，动态规划算法通常以⾃底向上的⽅式解各⼦问题，⽽贪⼼算法则通常以⾃顶向下的⽅式进⾏,以迭代的⽅式作出相继的贪⼼选择，每作⼀次贪⼼选择就将所求问题简化为⼀个规模更⼩的⼦问题。

对于⼀个具体问题，要确定它是否具有贪⼼选择性质，我们必须证明每⼀步所作的贪⼼选择最终导致问题的⼀个整体最优解。

通常可以⽤我们在证明活动安排问题的贪⼼选择性质时所采⽤的⽅法来证明。

⾸先考察问题的⼀个整体最优解，并证明可修改这个最优解，使其以贪⼼选择开始。

⽽且作了贪⼼选择后，原问题简化为⼀个规模更⼩的类似⼦问题。

然后，⽤数学归纳法证明，通过每⼀步作贪⼼选择，最终可得到问题的⼀个整体最优解。

其中，证明贪⼼选择后的问题简化为规模更⼩的类似⼦问题的关键在于利⽤该问题的最优⼦结构性质。

2．最优⼦结构性质当⼀个问题的最优解包含着它的⼦问题的最优解时，称此问题具有最优⼦结构性质。

问题所具有的这个性质是该问题可⽤动态规划算法或贪⼼算法求解的⼀个关键特征。

(1) (1)，xi(2)源自，…，xi(mi)
(mi-1)
，|Si| =mi，i=1，2，…，n。从根开始，
让 T 的第 I 层的每一个结点都有 mi 个儿子。这 mi 个儿子到它们的双亲的边，按从左到右的 ，xi+1
(2)
，…，xi+1
，i=0，1，2，…，n-1。照这种构造方式，E
中的一个 n 元组（x1，x2，…，xn）对应于 T 中的一个叶子结点，T 的根到这个叶子结点的路 径上依次的 n 条边的权分别为 x1，x2，…，xn，反之亦然。另外，对于任意的 0≤i≤n-1，E 中 n 元组（x1，x2，…，xn）的一个前缀 I 元组（x1，x2，…，xi）对应于 T 中的一个非叶子 结点，T 的根到这个非叶子结点的路径上依次的 I 条边的权分别为 x1，x2，…，xi，反之亦 然。特别，E 中的任意一个 n 元组的空前缀（） ，对应于 T 的根。 因而， 在 E 中寻找问题 P 的一个解等价于在 T 中搜索一个叶子结点， 要求从 T 的根到该
叶子结点的路径上依次的 n 条边相应带的 n 个权 x1，x2，…，xn 满足约束集 D 的全部约束。 在 T 中搜索所要求的叶子结点， 很自然的一种方式是从根出发， 按深度优先的策略逐步深入， 即依次搜索满足约束条件的前缀 1 元组（x1i） 、前缀 2 元组（x1，x2） 、…，前缀 I 元组（x1， x2，…，xi） ，…，直到 i=n 为止。 在回溯法中， 上述引入的树被称为问题 P 的状态空间树； 树 T 上任意一个结点被称为问 题 P 的状态结点； 树 T 上的任意一个叶子结点被称为问题 P 的一个解状态结点； 树 T 上满足 约束集 D 的全部约束的任意一个叶子结点被称为问题 P 的一个回答状态结点， 它对应于问题 P 的一个解。

算法分析与设计2016/2017(2）实验题目装载问题5种解法学生姓名学生学号学生班级任课教师提交日期2017计算机科学与技术学目录一问题定义 (2)二解决方案 (2)1优先队列式分支限界法求解 (2)1。

3运行结果 (12)2队列式分支限界法求解 (12)2。

1算法分析 (12)2。

2代码 (13)2.3测试截图 (21)3回朔法-迭代 (21)3.1算法分析 (21)3。

2代码 (21)3.3测试截图 (25)4回朔法-递归 (25)4。

1算法分析 (25)4。

2代码 (25)4.3测试截图 (30)5贪心算法 (30)5.1算法分析 (30)5.2代码 (30)5。

3测试截图 (33)一问题定义有一批共有 n 个集装箱要装上两艘载重量分别为 c1 和 c2 的轮船，其中集装箱 i 的重量为 w［i]，且重量之和小于(c1 + c2）。

装载问题要求确定是否存在一个合理的装载方案可将这 n 个集装箱装上这两艘轮船。

如果有，找出一种装载方案.二解决方案1优先队列式分支限界法求解1.1算法分析活结点x在优先队列中的优先级定义为从根结点到结点x的路径所相应的载重量再加上剩余集装箱的重量之和。

优先队列中优先级最大的活结点成为下一个扩展结点.以结点x为根的子树中所有结点相应的路径的载重量不超过它的优先级。

子集树中叶结点所相应的载重量与其优先级相同。

在优先队列式分支限界法中，一旦有一个叶结点成为当前扩展结点,则可以断言该叶结点所相应的解即为最优解。

此时可终止算法.1.2代码1。

2-1////MaxHeap.htemplate<class T〉class MaxHeap{public：MaxHeap(int MaxHeapSize = 10）;~MaxHeap() {delete [］heap;｝int Size() const {return CurrentSize;}T Max（){ //查找if (CurrentSize == 0)｛throw OutOfBounds（)；}return heap[1];｝MaxHeap<T>& Insert(const T＆x）; //增MaxHeap<T>& DeleteMax（T& x)；//删void Initialize(T a［]，int size, int ArraySize）;private:int CurrentSize，MaxSize；T ＊heap；// element array｝;template<class T〉MaxHeap〈T〉::MaxHeap（int MaxHeapSize）｛// Max heap constructor。