小学思维数学讲义：几何中的重叠问题-带详解

第十八讲重叠问题第一部分：趣味数学灰太狼的诡计灰太狼去参加羊村举行的运动会。

在百米赛跑中，灰太狼得了第四名，很生气。

第二天，灰太狼找到冠军喜羊羊，对他说：“咱俩再比一比，如果这次你还是第一，我才佩服你呢！”他俩来到操场。

34米32米68米灰太狼说：“我沿着整个操场跑一圈是200米。

你沿着东操场跑两圈，也是200米。

”“行。

开始吧！”喜羊羊说道。

结果灰太狼先跑完全程，得了第一。

喜羊羊想不通，说：“我比你跑得快，怎么今天没跑过你呢？”小朋友们，你们知道是怎么回事吗？快来帮帮喜羊羊吧！分析：灰太狼跑了4个34米和2个32米，喜羊羊跑了4个34米和4个32米，比灰太狼多跑了2个32米。

答案：灰太狼：4×34+2×32=136+64=200（米）喜羊羊：4×34+4×32=136+128=264（米）所以灰太狼跑得快，得了第一。

第二部分：奥数小练三（1）班准备给参加班级绘画比赛的16位同学和参加朗读比赛的12位同学每人发一份纪念品，当中队长玲玲将28份纪念品发下去时，却多出5份，这是怎么回事？对了，因为有5位同学既参加了绘画比赛，又参加了朗读比赛，所以奖品就多出了5份。

数学中，我们将这样的问题称为重叠问题。

解答重叠问题要用到数学中的一个重要原理——包含与排除原理，即当两个计数部分有重复包含时，为了不重复计数，应从它们的和中排除重复部分。

解答重叠问题的应用题，必须从条件入手进行认真的分析，有时还要画出图示，借助图形进行思考，找出哪些是重复的，重复了几次？明确求的是哪一部分，从而找出解答方法。

【例题1】六一儿童节，学校门口挂了一行彩旗。

小张从前数起，红旗是第8面；从后数起，红旗是第10面。

这行彩旗共多少面？【思路导航】根据题意，画出下图：从图上可以看出，从前数起红旗是第8面，从后数起是第10面，这样红旗就数了两次，重复了一次，所以这行彩旗共有8＋10－1=17面。

练习1：1.小朋友排队做操，小明从前数起排在第4个，从后数起排在第7个。

1. 瞭解容斥原理二量重疊和三量重疊的內容；2. 掌握容斥原理的在組合計數等各個方面的應用．一、兩量重疊問題 在一些計數問題中，經常遇到有關集合元素個數的計算．求兩個集合並集的元素的個數，不能簡單地把兩個集合的元素個數相加，而要從兩個集合個數之和中減去重複計算的元素個數，即減去交集的元素個數，用式子可表示成：A B A B A B =+-(其中符號“”讀作“並”，相當於中文“和”或者“或”的意思；符號“”讀作“交”，相當於中文“且”的意思．)則稱這一公式為包含與排除原理，簡稱容斥原理．圖示如下:A 表示小圓部分，B 表示大圓部分，C 表示大圓與小圓的公共部分，記為：A B ，即陰影面積．圖示如下:A 表示小圓部分，B 表示大圓部分，C 表示大圓與小圓的公共部分，記為：A B ，即陰影面積．包含與排除原理告訴我們，要計算兩個集合A B 、的並集AB 的元素的個數，可分以下兩步進行：第一步：分別計算集合A B 、的元素個數，然後加起來，即先求A B +(意思是把A B 、的一切元素都“包含”進來，加在一起)；第二步：從上面的和中減去交集的元素個數，即減去C AB =(意思是“排除”了重複計算的元素個數)． 二、三量重疊問題A 類、B 類與C 類元素個數的總和A =類元素的個數B +類元素個數C +類元素個數-既是A 類又是B 類的元素個數-既是B 類又是C 類的元素個數-既是A 類又是C 類的元素個數+同時是A 類、B 類、C 類的元素個數．用符號表示為：A B C A B C A B B C A C A B C =++---+．圖示如下：教學目標知識要點7-7-3.幾何中的重疊問題1．先包含——A B +重疊部分A B 計算了2次，多加了1次；2．再排除——A B A B +-把多加了1次的重疊部分A B 減去．在解答有關包含排除問題時，我們常常利用圓圈圖(韋恩圖)來幫助分析思考．【例 1】 把長38釐米和53釐米的兩根鐵條焊接成一根鐵條．已知焊接部分長4釐米，焊接後這根鐵條有多長？【考點】幾何中的重疊問題 【難度】1星 【題型】解答【解析】 因為焊接部分為兩根鐵條的重合部分，所以，由包含排除法知，焊接後這根鐵條長3853487+-=(釐米)．【答案】87釐米【巩固】 把長23釐米和37釐米的兩根鐵條焊接成一根鐵條．已知焊接部分長3釐米，焊接後這根鐵條有多長？【考點】幾何中的重疊問題 【難度】1星 【題型】解答【解析】 焊接部分為兩根鐵條的重合部分，由包含排除法知，焊接後這根鐵條長：2337357+-=(釐米)．【答案】57釐米【例 2】 兩張長4釐米，寬2釐米的長方形紙擺放成如圖所示形狀．把它放在桌面上，覆蓋面積有多少平方釐米？【考點】幾何中的重疊問題 【難度】1星 【題型】解答例題精講圖中小圓表示A 的元素的個數，中圓表示B 的元素的個數，大圓表示C 的元素的個數．1．先包含：A B C ++ 重疊部分A B 、B C 、C A 重疊了2次，多加了1次． 2．再排除：A B C A B B C A C ++--- 重疊部分A B C 重疊了3次，但是在進行A B C ++- A B B C A C --計算時都被減掉了． 3．再包含：A B C A B B C A C A B C ++---+．图32厘米4厘米【解析】 兩個長方形如圖擺放時出現了重疊(見圖中的陰影部分)，重疊部分恰好是邊長為2釐米的正方形，如果利用兩個42⨯的長方形面積之和來計算被覆蓋桌面的面積，那麼重疊部分在兩個長方形面積中各被計算了一次，而實際上這部分只需計算一次就可以了．所以，被覆蓋面積=長方形面積之和-重疊部分．於是，被覆蓋面積4222212=⨯⨯-⨯=(平方釐米)．【答案】12釐米【巩固】 如圖3，一張長8釐米，寬6釐米，另一個正方形邊長為6釐米，它們中間重疊的部分是一個邊長為4釐米的正方形，求這個組合圖形的面積．【考點】幾何中的重疊問題 【難度】1星 【題型】解答图3【解析】 兩個圖形如圖擺放時出現了重疊(見圖中的陰影部分)，重疊部分恰好是邊長為4釐米的正方形，如果利用長方形和正方形面積之和來計算被覆蓋桌面的面積，那麼重疊部分在長方形和正方形面積中各被計算了一次，而實際上這部分只需計算一次就可以了．所以，組合圖形的面積=長方形面積+正方形面積-重疊部分．於是，組合圖形的面積：86664468⨯+⨯-⨯=(平方釐米)．【答案】68平方釐米【巩固】 一個長方形長12釐米，寬8釐米，另一個長方形長10釐米，寬6釐米，它們中間重疊的部分是一個邊長4釐米的正方形，求這個組合圖形的面積．【考點】幾何中的重疊問題 【難度】1星 【題型】解答【解析】 兩個長方形如圖擺放時出現了重疊(見圖中的陰影部分)，重疊部分恰好是邊長為4釐米的正方形，如果利用兩個長方形面積之和來計算被覆蓋桌面的面積，那麼重疊部分在兩個長方形面積中各被計算了一次，而實際上這部分只需計算一次就可以了．所以，組合圖形的面積=長方形面積之和-重疊部分．於是，組合圖形的面積12810644140=⨯+⨯-⨯=(平方釐米)．【答案】140平方釐米【例 3】三個面積均為50平方釐米的圓紙片放在桌面上(如圖)，三個紙片共同重疊的面積是10平方釐米．三個紙片蓋住桌面的總面積是100釐米．問：圖中陰影部分面積之和是多少？【考點】幾何中的重疊問題【難度】2星【題型】解答C BA10【解析】將圖中的三個圓標上A、B、C．根據包含排除法，三個紙片蓋住桌面的總面積=(A圓面積B+圓面積C+圓面積-）（A與B重合部分面積A+與C重合部分面積B+與C重合部分面積+）三個紙片共同重疊的面積，得：100505050A=++-（）（與B重合部分面積A+與C重合部分面積B+與C重合部分面積10+），得到A、B、C三個圓兩兩重合面積之和為：16010060-=平方釐米，而這個面積對應於圓上的那三個紙片共同重疊的面積的三倍與陰影部分面積的和，即：60103=⨯+陰影部分面積，則陰影部分面積為：603030-=(平方釐米)．【答案】30平方釐米【巩固】如圖，已知甲、乙、丙3個圓的面積均為30，甲與乙、乙與丙、甲與丙重合部分的面積分別為6，8，5，而3個圓覆蓋的總面積為73．求陰影部分的面積．【考點】幾何中的重疊問題【難度】2星【題型】解答【解析】設甲圓組成集合A，乙圓組成集合B，丙圓組成集合C．A B C===30，A B=6，B C=8，A C=5，A B C=73，而A B C=A B C+--A B B C A C A B C--+.有73=30×3-6-8-5+A B C，即A B C=2，即甲、乙、丙三者的公共面積(⑧部分面積)為2．那麼只是甲與乙(④)，乙與丙(⑥)，甲與丙(⑤)的公共的面積依次為6-2=4，8-2=6，5-2=3，所以有陰影部分(①、②、③部分之和)的面積為73-4-6-3-2=58．【答案】58【例 4】如圖，三角形紙板、正方形紙板、圓形紙板的面積相等，都等於60平方釐米．陰影部分的面積總和是40平方釐米，3張板蓋住的總面積是100平方釐米，3張紙板重疊部分的面積是多少平方釐米？【考點】幾何中的重疊問題【難度】3星【題型】解答【解析】了三次．所以三張紙重疊部分的面積60310040220（）(平方釐米)．=⨯--÷=【答案】20平方釐米【巩固】如圖所示，A、B、C分別是面積為12、28、16的三張不同形狀的紙片，它們重疊在一起，露在外面的總面積為38．若A與B、B與C的公共部分的面積分別為8、7，A、B、C這三張紙片的公共部分為3．求A與C公共部分的面積是多少？【考點】幾何中的重疊問題【難度】3星【題型】解答【解析】設A與C公共部分的面積為x，由包含與排除原理可得：⑴先“包含”：把圖形A、B、C的面積相加：12281656++=，那麼每兩個圖形的公共部分的面積都重複計算了1次，因此要排除掉．⑵再“排除”：5687x---，這樣一來，三個圖形的公共部分被全部減掉，因此還要再補回．⑶再“包含”：56873x---+，這就是三張紙片覆蓋的面積．根據上面的分析得：5687338x=．x---+=，解得：6【答案】6。

第十章重叠问题（讲义）教案章节：第十章重叠问题教材：小学数学七年级上册目标：1. 让学生了解重叠问题的概念和基本思路；2. 让学生能够运用所学知识解决重叠问题。

教学重点：让学生明确重叠问题的基本概念和基本思路。

教学难点：让学生能够灵活运用所学知识解决具体问题。

教学内容：1. 重叠问题的定义重叠问题是指两个或多个物体在一定的情况下重叠在一起，需要通过计算来求出它们的具体位置和大小等问题。

2. 重叠问题的基本思路a. 先理清要求解决的具体问题。

b. 利用图形加减法或平移法计算出每个物体的具体位置和大小。

c. 通过比较和调整计算出它们的重叠部分的位置、大小和形状。

d. 最后总结并验证计算结果。

教学过程：1. 导入新知识通过导图、图片和视频等多种形式让学生了解重叠问题的概念和基本思路。

2. 指导学生进行实际操作让学生通过实物和图形模拟进行重叠问题的实际操作，如两个圆形的重叠和交集问题等。

3. 分小组进行练习将学生分成若干小组，让每个小组自行设计两个或三个图形进行重叠问题的实际操作，并让其他小组进行验证和总结。

4. 进一步挑战让学生设计更加复杂的图形，进一步挑战重叠问题的难度，如三角形和正方形的重叠，在讲解的基础上让学生独立解决实际问题。

教学评价：1. 课上教师进行实时评价，对学生的问题作出及时回答和指导。

2. 课后学生进行个人和小组总结，将所学知识运用到实际生活中，提出反馈意见和建议。

教学延伸：1. 扩大应用范围将重叠问题应用到其他学科中，如自然科学、社会科学等有关科目中，帮助学生更好地理解和掌握相关内容。

2. 考虑个体差异针对不同学生的学习兴趣和能力差异，采用不同的教学方式和方法，帮助学生更好地学习和掌握相关知识。

教学延伸（续）3. 引导学生独立探究在教学中，应该多给予学生探究机会，通过实际操作和自主学习，帮助学生更好地理解和掌握相关知识，培养学生的独立思考和解决问题的能力。

4. 结合现实生活案例在教学中，应该和学生结合现实生活中的案例，如居民区的规划设计、交通布局等，让学生通过实际操作和运用所学知识，了解相关解决方案和应用技巧。

第06讲重叠问题（上）教学目标：1、理解简单的重叠问题，通过画图解决重叠问题；2、鼓励学员尽可能多的在纸上画一画，写一写重叠问题的相关问题，提升计算准确度和速度；3、丰富对直观的认识，发展形象思维，养成善于观察、善于思考的良好学习习惯。

教学重点：理解重叠问题，掌握重叠问题的解题思路和方法，让学生初步体会数学中的一个重要原理——容斥原理。

教学难点：理解什么是重叠问题，掌握重叠问题的解题方法。

教学过程：【环节一：预习讨论，案例分析】【知识回顾——温故知新】----参考时间-2分钟等量代换注意的问题：（1）寻找中间量；（2）当两个整体相等时，如果它们中的一部分相等，那么其余的部分一定也相等。

（3）用数学式子表示关系式，再寻找相同的量进行代换。

【知识回顾——上期巩固】----参考时间-3分钟已知○+△= 41，△+□=53，□+○=18，求○=（），△=（），□=（）。

解析部分：引导学生思考,从已知的三个等式可以看出：两个圆形、两个三角形、两个正方形的和是41+53+18=112千克，由此可以求出一个圆形、一个三角形、一个正方形的和，进而求出每一种图形的数值。

给予新学员的建议：教师可以引导学员先求出两个圆形、两个三角形、两个正方形的和；哈佛案例教学法：鼓励学生独立完成，课堂上分享解题方法。

参考答案：方法一：由○+△= 41，△+□=53，得□-○=12，结合□+○=18，根据和差问题，□=(18+12)÷2=15，△=53-15=38。

○=3。

方法二：上讲讲解室的解法，求得○+△+□=56，然后得□=15，△=38，○=3。

【预习题分析——本期预习】----参考时间-7分钟兔把两块一样长的木板，钉在一起，如果每块木板长25厘米，中间重叠部分长5厘米，钉好后木板有多长？解析部分：让学生思考，兔把两块木板钉起来，接口处有重叠部分。

钉好后的总长就是原来两个总长的和减去重叠部分。

重叠问题的关键：确定重叠部分。

第十四讲重叠问题【知识要点】重叠问题是数学思维训练中经常会遇到的问题，解答重叠问题要用到数学中的一个重要原理——包含与排除原理，即当两个计数部分有重复包含时，为了不重复计数，应从它们的和中排除重复部分。

解答重叠问题时会借助集合圈来帮助分析数量之间的关系，借助图形进行思考，找出哪些是重复的，重复了几次。

其基本方法一般有两种：1．求有重叠情况的两部分的和，可用原来两部分的和，减去重叠部分；2．求有重叠情况的两部分的和，还可以用分块计算的方法，即先分别算出互不重叠的各个部分，再把它们相加。

例题1、在一次期终考试中，某年级有24人英语得100分，有31人数学得100分，其中有10人英语、数学都得100分，这个年级英语或数学得100分的共有多少人?练习1、将两张面积都是30平方厘米的纸片叠放在桌面上，两张纸片在桌面上的覆盖面积是48平方厘米，两张纸片重合部分的面积是多少平方厘米?例题2、某班有26人参加体育比赛，其中参加跑步的有12人，参加跳绳的有18人，既参加跑步又参加跳绳的有多少人?练习2、一个歌舞表演团中，能表演独唱的有12人，能表演跳舞的有25人，两种都能表演的有3人。

这个表演队共有多少人能登台表演歌舞?例题3、四(1)班共有学生32人，其中有21人参加美术兴趣小组，有13人参加朗诵兴趣小组，有10人既参加美术兴趣小组又参加朗诵兴趣小组．这个班中没有参加兴趣小组的有多少人?练习3、一次春游中，某班34名同学去公园游玩，有25人划船，19人爬山，4名同学因身体不好既没划船又没爬山，既划船又爬山的有多少人?例题4、在一次测试中，某班有12人语文得满分，15人数学得满分，两门都得满分的有6人，两门都没得满分的有14人。

这个班共有多少人?练习4、在一次学校组织的竞赛中，三（1）班40名同学中，有18人参加数学竞赛，有22人参加作文竞赛，已知全班有5人既参加数学竞赛又参加作文竞赛，两种竞赛都没参加的有多少人?例题5、学校组织象棋和围棋棋比赛，共有48人参加比赛。

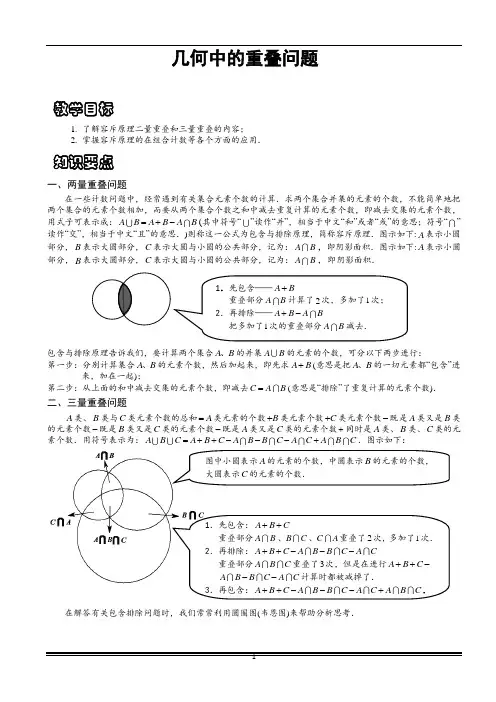
几何中的重叠问题1. 了解容斥原理二量重叠和三量重叠的内容；2. 掌握容斥原理的在组合计数等各个方面的应用．一、两量重叠问题在一些计数问题中，经常遇到有关集合元素个数的计算．求两个集合并集的元素的个数，不能简单地把两个集合的元素个数相加，而要从两个集合个数之和中减去重复计算的元素个数，即减去交集的元素个数，用式子可表示成：A B A B A B =+-(其中符号“”读作“并”，相当于中文“和”或者“或”的意思；符号“”读作“交”，相当于中文“且”的意思．)则称这一公式为包含与排除原理，简称容斥原理．图示如下:A 表示小圆部分，B 表示大圆部分，C 表示大圆与小圆的公共部分，记为：A B ，即阴影面积．图示如下:A 表示小圆部分，B 表示大圆部分，C 表示大圆与小圆的公共部分，记为：A B ，即阴影面积．包含与排除原理告诉我们，要计算两个集合A B 、的并集A B 的元素的个数，可分以下两步进行： 第一步：分别计算集合A B 、的元素个数，然后加起来，即先求A B +(意思是把A B 、的一切元素都“包含”进来，加在一起)；第二步：从上面的和中减去交集的元素个数，即减去C A B =(意思是“排除”了重复计算的元素个数)． 二、三量重叠问题A 类、B 类与C 类元素个数的总和A =类元素的个数B +类元素个数C +类元素个数-既是A 类又是B 类的元素个数-既是B 类又是C 类的元素个数-既是A 类又是C 类的元素个数+同时是A 类、B 类、C 类的元素个数．用符号表示为：A B C A B C A B B C A C A B C =++---+．图示如下：在解答有关包含排除问题时，我们常常利用圆圈图(韦恩图)来帮助分析思考．教学目标 知识要点 1．先包含——A B + 重叠部分A B 计算了2次，多加了1次； 2．再排除——A B A B +- 把多加了1次的重叠部分A B 减去．图中小圆表示A 的元素的个数，中圆表示B 的元素的个数，大圆表示C 的元素的个数．1．先包含：A B C ++ 重叠部分A B 、B C 、C A 重叠了2次，多加了1次． 2．再排除：A B C A B B C A C ++--- 重叠部分A B C 重叠了3次，但是在进行A B C ++- A B B C A C --计算时都被减掉了． 3．再包含：A B C A B B C A C A B C ++---+．【例 1】 把长38厘米和53厘米的两根铁条焊接成一根铁条．已知焊接部分长4厘米，焊接后这根铁条有多长？【考点】几何中的重叠问题 【难度】1星 【题型】解答【解析】 因为焊接部分为两根铁条的重合部分，所以，由包含排除法知，焊接后这根铁条长3853487+-=(厘米)．【答案】87厘米【巩固】 把长23厘米和37厘米的两根铁条焊接成一根铁条．已知焊接部分长3厘米，焊接后这根铁条有多长？【考点】几何中的重叠问题 【难度】1星 【题型】解答【解析】 焊接部分为两根铁条的重合部分，由包含排除法知，焊接后这根铁条长：2337357+-=(厘米)．【答案】57厘米【例 2】 两张长4厘米，宽2厘米的长方形纸摆放成如图所示形状．把它放在桌面上，覆盖面积有多少平方厘米？【考点】几何中的重叠问题 【难度】1星 【题型】解答图32厘米4厘米【解析】 两个长方形如图摆放时出现了重叠(见图中的阴影部分)，重叠部分恰好是边长为2厘米的正方形，如果利用两个42⨯的长方形面积之和来计算被覆盖桌面的面积，那么重叠部分在两个长方形面积中各被计算了一次，而实际上这部分只需计算一次就可以了．所以，被覆盖面积=长方形面积之和-重叠部分．于是，被覆盖面积4222212=⨯⨯-⨯=(平方厘米)．【答案】12厘米【巩固】 如图3，一张长8厘米，宽6厘米，另一个正方形边长为6厘米，它们中间重叠的部分是一个边长为4厘米的正方形，求这个组合图形的面积．【考点】几何中的重叠问题 【难度】1星 【题型】解答图3 【解析】 两个图形如图摆放时出现了重叠(见图中的阴影部分)，重叠部分恰好是边长为4厘米的正方形，如果利用长方形和正方形面积之和来计算被覆盖桌面的面积，那么重叠部分在长方形和正方形面积中各被计算了一次，而实际上这部分只需计算一次就可以了．所以，组合图形的面积=长方形面积+正方形面积-重叠部分．于是，组合图形的面积：86664468⨯+⨯-⨯=(平方厘米)．【答案】68平方厘米【巩固】 一个长方形长12厘米，宽8厘米，另一个长方形长10厘米，宽6厘米，它们中间重叠的部分是一个边长4厘米的正方形，求这个组合图形的面积．【考点】几何中的重叠问题 【难度】1星 【题型】解答例题精讲12【解析】 两个长方形如图摆放时出现了重叠(见图中的阴影部分)，重叠部分恰好是边长为4厘米的正方形，如果利用两个长方形面积之和来计算被覆盖桌面的面积，那么重叠部分在两个长方形面积中各被计算了一次，而实际上这部分只需计算一次就可以了．所以，组合图形的面积=长方形面积之和-重叠部分．于是，组合图形的面积12810644140=⨯+⨯-⨯=(平方厘米)．【答案】140平方厘米【例 3】 三个面积均为50平方厘米的圆纸片放在桌面上(如图)，三个纸片共同重叠的面积是10平方厘米．三个纸片盖住桌面的总面积是100厘米．问：图中阴影部分面积之和是多少？【考点】几何中的重叠问题 【难度】2星 【题型】解答CBA10 【解析】 将图中的三个圆标上A 、B 、C ．根据包含排除法，三个纸片盖住桌面的总面积=(A 圆面积B +圆面积C +圆面积-）（A 与B 重合部分面积A +与C 重合部分面积B +与C 重合部分面积+）三个纸片共同重叠的面积，得：100505050A =++-（）（与B 重合部分面积A +与C 重合部分面积B +与C 重合部分面积10+），得到A 、B 、C 三个圆两两重合面积之和为：16010060-=平方厘米，而这个面积对应于圆上的那三个纸片共同重叠的面积的三倍与阴影部分面积的和，即：60103=⨯+阴影部分面积，则阴影部分面积为：603030-=(平方厘米)．【答案】30平方厘米【巩固】 如图，已知甲、乙、丙3个圆的面积均为30，甲与乙、乙与丙、甲与丙重合部分的面积分别为6，8，5，而3个圆覆盖的总面积为73．求阴影部分的面积．【考点】几何中的重叠问题 【难度】2星 【题型】解答【解析】 设甲圆组成集合A ，乙圆组成集合B ，丙圆组成集合C ． A B C ===30，A B =6，B C =8，A C =5，A B C =73，而A B C =A B C +--A B B C A C A B C --+.有73=30×3-6-8-5+AB C ，即A B C =2，即甲、乙、丙三者的公共面积(⑧部分面积)为2．那么只是甲与乙(④)，乙与丙(⑥)，甲与丙(⑤)的公共的面积依次为6-2=4，8-2=6，5-2=3，所以有阴影部分(①、②、③部分之和)的面积为73-4-6-3-2=58．【答案】58【例 4】 如图，三角形纸板、正方形纸板、圆形纸板的面积相等，都等于60平方厘米．阴影部分的面积总和是40平方厘米，3张板盖住的总面积是100平方厘米，3张纸板重叠部分的面积是多少平方厘米？【考点】几何中的重叠问题 【难度】3星【题型】解答【解析】 阴部分的面积60310040220=⨯--÷=（）(平方厘米)．【答案】20平方厘米【巩固】如图所示，A、B、C分别是面积为12、28、16的三张不同形状的纸片，它们重叠在一起，露在外面的总面积为38．若A与B、B与C的公共部分的面积分别为8、7，A、B、C这三张纸片的公共部分为3．求A与C公共部分的面积是多少？【考点】几何中的重叠问题【难度】3星【题型】解答【解析】设A与C公共部分的面积为x，由包含与排除原理可得：⑴先“包含”：把图形A、B、C的面积相加：12281656++=，那么每两个图形的公共部分的面积都重复计算了1次，因此要排除掉．⑵再“排除”：5687x---，这样一来，三个图形的公共部分被全部减掉，因此还要再补回．⑶再“包含”：56873---+，这就是三张纸片覆盖的面积．x根据上面的分析得：5687338x=．x---+=，解得：6【答案】6。