透视投影与正投影相关函数介绍
- 格式:doc
- 大小:103.00 KB
- 文档页数:3

投影转换公式范文投影转换的目的是将三维物体的形状、尺寸、方向等信息映射到二维平面上,以便于在计算机屏幕上显示或进行进一步处理。
其中最常用的投影转换有透视投影和平行投影两种。
透视投影是模拟人眼看到的投影效果。
当物体离观察者比较近时,离观察者越近的物体映射到平面上的尺寸越大;当物体离观察者比较远时,离观察者越远的物体映射到平面上的尺寸越小。
透视投影的数学表达式如下:```x'=(x*f)/(z+d)y'=(y*f)/(z+d)```其中,(x,y,z)是三维物体上的一个点,(x',y')是其在二维平面上的投影点,f是焦距,d是观察者到投影平面的距离。
平行投影是保持物体的形状和尺寸不变,将其映射到平行于观察视线的平面上。
平行投影的数学表达式如下:```x' = x + dxy' = y + dy```其中,(x, y, z)是三维物体上的一个点,(x', y')是其在二维平面上的投影点,dx和dy是投影平面的偏移量,用于控制投影的位置。
除了透视投影和平行投影,还有其他各种形式的投影转换公式。
比如等角投影、斜投影、正射投影等等。
不同的投影转换公式适用于不同的应用场景和需求。
在计算机图形学中,投影转换通常是在视景体的局部坐标系中进行的。
视景体是一个六面体,用于限定需要显示的物体范围。
常见的视景体包括矩形视景体、正交视景体、透视视景体等。
在进行投影转换时,需要将三维物体先从局部坐标系转换到世界坐标系,然后再进行投影转换到二维平面上。
投影转换还涉及到一些常见的问题和技巧,比如消失点的计算、背面剔除、深度缓冲等。
这些问题和技巧都是为了提高投影转换的效果和速度,使得二维平面上的投影能够尽可能地还原出三维物体的形状和尺寸。
总结起来,投影转换公式是将三维空间中的点映射到二维平面上的数学公式。
不同的投影转换公式适用于不同的应用场景和需求。
投影转换涉及到视景体、局部坐标系、世界坐标系等概念。

数学投影知识点总结投影是数学中一个重要的概念,在不同的数学分支中,都有着广泛的应用。
在几何学中,就有投影的相关概念。
同时,在线性代数,微积分等数学领域中也存在着对投影的研究和应用。
本文就数学投影的相关知识点进行总结,希望对读者有所帮助。
一、几何投影在几何学中,投影是一个非常重要的概念。
可以通过直线或者平面对物体进行投影,来得到与原物体相关的信息。
投影可以分为平行投影和透视投影。
平行投影是指从一个点或者平面上进行投影,透视投影是指从一个视点或者视平面上进行投影。
1.1 二维投影在二维空间中,通过一个直线对一个点或者物体进行投影。
例如,我们常常在平面上投影得到某个物体的阴影,来了解它的形状和大小。
在几何学中,我们可以通过简单的几何图形来了解二维投影的一些性质。
例如,一个线段在平行于投影直线的平面上的投影长度等于原线段长度乘以一个比例因子。
这个比例因子与投影直线的夹角有关。
这就是二维投影的一个基本知识点。
1.2 三维投影在三维空间中,投影的概念就更加复杂。
我们可以通过一个平面对一个三维物体进行投影,来得到它在平面上的投影。
这就是三维空间中的投影。
在几何学中,我们可以通过向量和矩阵的方法来研究三维投影。
通过线性代数的知识,可以得到在一个给定坐标系下,一个点在一个给定平面上的投影的坐标。
这就是三维投影的基本知识点。
1.3 投影的应用在几何学中,投影有着广泛的应用。
例如,在工程图学中,我们需要根据三维物体的投影来绘制其对应的二维工程图。
这就需要我们对三维投影有着深刻的认识。
在建筑学中,我们需要根据建筑物的三维模型来绘制其二维图纸。
这也需要我们对投影有着深入的了解。
因此,对于投影的几何学知识点的掌握是非常重要的。
二、线性代数中的投影在线性代数中,投影是一个重要的概念。
特别是在向量空间和点集投影中,投影的研究有着广泛的应用。
2.1 向量投影在线性代数中,我们经常需要计算一个向量在另一个向量上的投影。
这就是向量投影。

透视投影透视投影是用中心投影法将形体投射到投影面上,从而获得的一种较为接近视觉效果的单面投影图。
它具消失感、距离感、相同大小的形体呈现出有规律的变化等一系列的透视特性,能逼真地反映形体的空间形象。
透视投影也称为透视图,简称透视。
在建筑设计过程中,透视图常用来表达设计对象的外貌,帮助设计构思,研究和比较建筑物的空间造型和立面处理,是建筑设计中重要的辅助图样。
透视投影符合人们心理习惯,即离视点近的物体大,离视点远的物体小,远到极点即为消失,成为灭点。
它的视景体类似于一个顶部和底部都被切除掉的棱椎,也就是棱台。
这个投影通常用于动画、视觉仿真以及其它许多具有真实性反映的方面。
在平行投影中,图形沿平行线变换到投影面上;对透视投影,图形沿收敛于某一点的直线变换到投影面上,此点称为投影中心,相当于观察点,也称为视点。
平行投影和透视投影区别在于透视投影的投影中心到投影面之间的距离是有限的,而平行投影的投影中心到投影面之间的距离是无限的。
当投影中心在无限远时,投影线互相平行,所以定义平行投影时,给出投影线的方向就可以了,而定义透视投影时,需要指定投影中心的具体位置平行投影保持物体的有关比例不变,这是三维绘图中产生比例图画的方法。
物体的各个面的精确视图可以由平行投影得到。
另一方面,透视投影不保持相关比例,但能够生成真实感视图。
对同样大小的物体,离投影面较远的物体比离投影面较近物体的投影图象要小,产生近大远小的效果.透视投影的原理和实现by Goncely摘要:透视投影是3D渲染的基本概念,也是3D程序设计的基础。
掌握透视投影的原理对于深入理解其他3D渲染管线具有重要作用。
本文详细介绍了透视投影的原理和算法实现,包括透视投影的标准模型、一般模型和屏幕坐标变换等,并通过VC实现了一个演示程序。
1 概述在计算机三维图像中,投影可以看作是一种将三维坐标变换为二维坐标的方法,常用到的有正交投影和透视投影。
正交投影多用于三维健模,透视投影则由于和人的视觉系统相似,多用于在二维平面中对三维世界的呈现。
3d图形程序,就一定会做坐标变换。
而谈到坐标变换,就不得不提起投影变换,因为它是所有变换中最不容易弄懂的。
但有趣的是,各种关于透视变换的文档却依然是简之又简,甚至还有前后矛盾的地方。
看来如此这般光景,想要弄清楚它,非得自己动手不可了。
所以在下面的文章里,作者尝试推导一遍这个难缠的透视变换,然后把它套用到DX和PS2lib 的实例中去。
1.一般概念所谓透视投影变换,就是view 空间到project 空间的带透视性质的坐标变换步骤(这两个空间的定义可以参考其他文档和书籍)。
我们首先来考虑它应该具有那些变换性质。
很显然,它至少要保证我们在view空间中所有处于可视范围内的点通过变换之后,统统落在project空间的可视区域内。
好极了,我们就从这里着手——先来看看两个空间的可视区域。
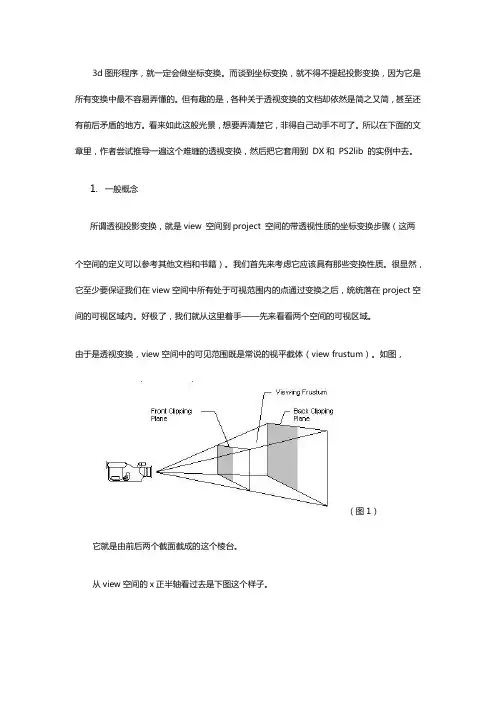
由于是透视变换,view空间中的可见范围既是常说的视平截体(view frustum)。
如图,(图1)它就是由前后两个截面截成的这个棱台。
从view空间的x正半轴看过去是下图这个样子。
(图2)接下来是project空间的可视范围。
这个空间应当是处于你所见到的屏幕上。
实际上将屏幕表面视作project空间的xoy平面,再加一条垂直屏幕向里(或向外)的z轴(这取决于你的坐标系是左手系还是右手系),这样就构成了我们想要的坐标系。
好了,现在我们可以用视口(view port)的大小来描述这个可视范围了。
比如说全屏幕640*480的分辨率,原点在屏幕中心,那我们得到的可视区域为一个长方体,它如下图(a)所示。
(图3)但是,这样会带来一些设备相关性而分散我们的注意力,所以不妨先向DirectX文档学学,将project空间的可视范围定义为x∈[-1,1], y∈[-1,1], z∈[0,1]的一个立方体(上图b)。
这实际上可看作一个中间坐标系,从这个坐标系到上面我们由视口得出的坐标系,只需要对三个轴向做一些放缩和平移操作即可。
另外,这个project坐标系对clip操作来说,也是比较方便的。




投影与透视知识点总结投影与透视是建筑、设计、绘画、摄影等领域中非常重要的概念,它们影响着我们的视觉感知和空间表现。
在本文中,我们将对投影与透视的基本原理、应用以及技术进行总结和分析。
1. 投影基本原理投影是一种几何学上的技术,它以一定的方式将三维空间中的物体投射到一个二维平面上,从而使得我们可以在平面上观察和分析这些物体。
在投影的过程中,需要考虑到物体、投影面和视点的空间关系。
根据不同的投影方式,可以将投影分为平行投影和透视投影。
1.1 平行投影平行投影是指在投影过程中,光线是平行的,物体在投影面上的形状和尺寸与实际物体的形状和尺寸完全一致。
平行投影主要包括正射投影和斜投影两种方式。
正射投影是指投影面与物体的关系是垂直的,而斜投影是指投影面与物体的关系是倾斜的。
平行投影的特点是投影形体的比例尺不变,适用于工程图、建筑图等。
1.2 透视投影透视投影是指在投影过程中,光线是经过物体和观察者的,具有一定的角度和距离。
这种投影方式具有远大近小和空间感的特点,更符合人眼观察的实际情况。
透视投影在绘画、建筑、摄影等领域中被广泛应用。
2. 透视基本原理透视是指在投影过程中,根据离观察者的距离远近和物体的大小来改变物体在平面上的形状和尺寸。
通过透视投影可以在平面上表现出空间的深度和远近关系,具有较强的艺术表现力和空间感。
透视主要包括单点透视、双点透视和三点透视三种方式。
2.1 单点透视单点透视是在透视投影过程中,根据物体远近关系,将物体在平面上的形状和尺寸进行递减处理,使得远处的物体看起来比较小,近处的物体看起来比较大。
在单点透视中,观察者眼睛、投影面和物体三者关系共线,呈现出一种非常明显的远大近小效果。
因此,单点透视也被称为中心透视。
2.2 双点透视双点透视是在透视投影过程中,根据物体在水平方向的远近关系,将物体在平面上的形状和尺寸进行递减处理。
在双点透视中,观察者的眼睛位于一个点上,投影面位于另一个点上,观察者的眼睛与投影面之间的连线与物体在水平方向的远近关系一致,使得物体在平面上的形状和尺寸表现出立体感。

透视函数的使用方法透视函数是现代数学和几何学中的一个重要工具,它能够帮助我们更好地理解和解决各种问题。
在本文中,我将向大家介绍透视函数的使用方法以及其在不同领域的应用。
首先,我们来了解一下透视函数的定义和基本概念。
透视函数是一种将空间中的物体影射到平面上的数学函数,它能够保持物体在空间中的相对位置关系,并将其映射到平面上的透视投影上。
透视函数由相机的焦距、观察角度等参数来确定,不同的参数组合会产生不同的投影效果。
在使用透视函数时,我们首先需要确定透视中心,也就是相机的位置。
然后,我们可以根据物体在空间中的位置和透视中心的距离来计算出物体在平面上的投影位置。
透视函数常用的数学表示方式是通过矩阵运算来实现的,我们可以通过矩阵乘法将物体的坐标转化为平面上的坐标。
透视函数在几何学和计算机图形学中有着广泛的应用。
例如,在建筑设计中,我们可以利用透视函数来模拟建筑物在现实世界中的投影效果,从而可以更好地理解和评估建筑的外观和空间布局。
在地理学中,透视函数可以用来制作地图,将地球表面的平面投影到纸面上,以便于我们进行测量和分析。
此外,透视函数还被广泛应用于艺术领域。
在绘画和摄影中,透视函数可以帮助我们更好地描绘和捕捉物体的形状和体积感。
通过运用透视函数,我们可以创建出更加逼真和立体的图像,使观众能够更好地体验到作品所传达的意境和情感。
在数学建模和科学研究中,透视函数也扮演着重要的角色。
例如,在物理学中,透视函数可以用来模拟光线的传播和折射,从而可以预测和解释光学现象。
在经济学中,透视函数可以用来分析市场行为和消费者偏好,帮助企业和政府制定更合理的决策。
综上所述,透视函数是一个非常有用的工具,它可以帮助我们更好地理解和解决各种问题。
无论是在建筑设计、地理学、艺术领域还是数学建模和科学研究中,透视函数都发挥着重要的作用。
通过学习和应用透视函数,我们可以提高自己的思维能力和问题解决能力,拓宽自己的知识领域。
因此,我们应该加强对透视函数的学习和掌握,发挥其在实践中的巨大潜力。

投影变换投影变换就是要确定一个取景体积,其作用有两个:1). 确定物体投影到屏幕的方式,即是透视投影还是正交投影。
2). 确定从图象上裁剪掉哪些物体或物体的某些部分。
投影变换包括透视投影和正交投影(平行投影)。
●透视投影透视投影的示意图如下,其取景体积是一个截头锥体,在这个体积内的物体投影到锥的顶点,用glFrustum()函数定义这个截头锥体,这个取景体积可以是不对称的,计算透视投影矩阵M,并乘以当前矩阵C,使C=CM。
void glFrustum(GLdouble left,GLdouble right,GLdouble bottom,GLdouble top,GLdouble near,GLdouble far);该函数以透视矩阵乘当前矩阵left, right 指定左右垂直裁剪面的坐标。
bottom,top 指定底和顶水平裁剪面的坐标。
near,far 指定近和远深度裁剪面的距离,两个距离一定是正的。
程序函数gluPerspective()可以创建一个与调用glFrustum()所得到的同样形状的视图体,它创建的是一个沿视线关于x和y轴均对称的平截台体,在很多实际应用中都采用函数gluPerspective()。
void gluPerspective(GLdouble fovy,GLdouble aspect, GLdouble zNear,GLdouble zFar);fovy是在x-z平面内视区的角度,其值必须在区间【0.0,180.0】内。
Aspect为长宽比,是平截台体的宽度与高度之比。
zNear和zFar的值是视点(沿z轴负向)与两个裁剪平面的距离。
参数恒为正。
图1透视投影示意图●正交投影正交投影的示意图见下:其取景体积是一个各面均为矩形的六面体,用glOrtho()函数创建正交平行的取景体积,计算正交平行取景体积矩阵M,并乘以当前矩阵C,使C=CM。
void glOrtho(Gldouble left,Gldouble right,Gldouble bottom,Gldouble top,Gldoublenear,Gldouble far);该函数以正交投影矩阵乘当前矩阵。

matlab投影函数在MATLAB中,有几种不同的函数可以用来进行投影处理。
投影是将三维物体映射到一个二维平面或图像上的过程。
以下是一些常用的MATLAB投影函数:1. perspective函数:perspective函数可以用于生成透视投影。
透视投影是通过将远离观察者的对象看起来较小来模拟现实世界中的透视效果。
这个函数接受一个3x4的投影矩阵作为输入,输出是一个透视变换的新图像。
2. orthographic函数:orthographic函数可以用于生成正交投影。
正交投影是一种将物体投影到平行于观察方向的平面上的投影方式。
这个函数接受一个3x4的投影矩阵作为输入,并返回一个正交变换的新图像。
3. imtransform函数:imtransform函数可以用于进行任意的二维图像变换,包括投影变换。
它接受一个二维变换矩阵作为输入,并返回一个经过变换的新图像。
4. projective2d对象:MATLAB中的projective2d对象代表一个二维的投影变换。
这个对象可以用来进行各种类型的二维变换,包括投影变换。
它可以通过设置变换矩阵的值来定义不同的投影变换。
5. tranformPointsForward函数:transformPointsForward函数可以用于将二维点集进行投影变换。
它接受一个变换矩阵和一个二维点坐标的矩阵作为输入,并返回经过变换后的点坐标。
6. imshow函数:imshow函数可以显示图像,并可以在显示之前应用其中一种类型的变换。
例如,可以使用imshow函数来显示一个经过投影变换后的图像。
7. plot函数:plot函数可以用来绘制二维图形,也可以用于绘制一个经过投影变换后的点集。
这可以通过将二维点集的坐标作为输入,然后在进行投影变换之后使用plot函数进行绘制。
MATLAB提供了许多功能强大的函数来进行投影处理。
以上列举的只是其中一些常用的函数。
使用这些函数,可以对三维物体进行各种类型的投影处理,并将它们映射到二维平面或图像上。
OpenGL图形变换OpenGL图形软件包是为三维应用设计的,其中包含了大量的有关三维变换的操作,二维变换则可以看作是三维变换的特例。
OpenGL中常用的变换包括模型视图变换、投影变换和视见区变换。
一、矩阵堆栈在计算机图形学中,所有的变换都是通过矩阵乘法来实现的,即将三维形体顶点构成的齐次坐标矩阵乘以三维变换矩阵就得到了变换后的形体顶点的齐次坐标矩阵,这样只要求出形体的三维变换矩阵,就可以得到变换后的形体。
在OpenGL中,对象的坐标变换也是通过矩阵来实现的。
OpenGL中包含了两个重要的矩阵:模型视图矩阵和投影矩阵,其中模型视图矩阵用于物体的模型视图变换,投影矩阵用于投影变换。
一般来说,在进行矩阵操作之前,需要指定当前操作的矩阵对象,这可以使用函数:glMatrixMode(GLenum mode);定义。
其中当mode取GL_MODELVIEW时,表示对模型视图矩阵进行操作;当mode取GL_PROJECTION时表示对投影矩阵进行操作,并且一旦设置了当前操作矩阵,它就将保持为当前的矩阵对象,直到再次调用函数glMatrixMode修改它为止。
默认情况下,系统处理的当前矩阵是模型视图矩阵。
OpenGL为模型视图矩阵和投影矩阵各维护着一个“矩阵堆栈”,其中堆栈的栈顶矩阵就是当前的模型视图矩阵或投影矩阵。
在调用变换函数的时候,系统自动计算变换函数对应的变换矩阵与当前操作的矩阵堆栈栈顶矩阵的乘积,并置为栈顶矩阵,绘制图形时使用栈顶矩阵作为图形的变换矩阵。
矩阵堆栈主要用来保存和恢复矩阵的状态。
OpenGL中利用函数:void glPushMatrix(void);void glPopMatrix(void);实现矩阵堆栈的操作。
其中函数glPushMatrix将当前矩阵堆栈的栈顶矩阵复制一个,并将其压入当前矩阵堆栈,以保存当前变换矩阵。
函数glPopMatrix用于将当前矩阵堆栈的栈顶矩阵弹出,这样,堆栈中的下一个矩阵变为栈顶矩阵(当前变换矩阵),用来恢复当前变换矩阵原先的状态。
透视投影的详细解释(转载)本⽂乃<投影矩阵的推导>译⽂,原⽂地址为:译者: 流星上的潴如需转载,请注明出处,感谢!在3D图形程序的基本矩阵变换中,投影矩阵是其中⽐较复杂的。
平移和缩放浏览⼀下就能理解,旋转矩阵只要掌握了三⾓函数知识也可以理解,但投影矩阵有点棘⼿。
如果你曾经看过投影矩阵,你会发现你的常识不⾜以告诉你它是怎么来的。
⽽且,我在⽹上还未看到许多关于如何推导投影矩阵的教程资源。
本⽂的话题就是如何推导投影矩阵。
对于刚刚开始接触3D图形的⼈,我应该指出,理解投影矩阵如何推导可能是我们对于数学的好奇⼼,它不是必须的。
你可以只⽤公式,并且如果你⽤像Direct3D那样的图形API,你甚⾄都不需要使⽤公式,图形API会为你构建⼀个投影矩阵。
所以,如果本⽂看起来有点难,不要害怕。
只要你理解了投影矩阵做了什么,你没必要在你不想的情况下关注它是怎么做的。
本⽂是给那些想了解更多的程序员的。
概述: 什么是投影?计算机显⽰器是⼀个⼆维表⾯,所以如果你想显⽰三维图像,你需要⼀种⽅法把3D⼏何体转换成⼀种可作为⼆维图像渲染的形式。
那也正是投影做的。
拿⼀个简单的例⼦来说,⼀种把3D对象投影到2D表⾯的⽅法是简单的把每个坐标点的z坐标丢弃。
对⽴⽅体来说,看上去可能像图1:图1: 通过丢弃Z坐标投影到XY平⾯当然,这过于简单,并且在⼤多数情况下不是特别有⽤。
⾸先,根本不会投影到⼀个平⾯上;相反,投影公式将变换你的⼏何体到⼀个新的空间体中,称为规范视域体(canonical view volume),规范视域体的精确坐标可能在不同的图形API之间互不相同,但作为讨论起见,把它认为是从(-1, -1, 0)延伸⾄(1, 1, 1)的盒⼦,这也是Direct3D中使⽤的。
⼀旦所有顶点被映射到规范视域体,只有它们的x和y坐标被⽤于映射到屏幕上。
这并不代表z坐标是⽆⽤的,它通常被深度缓冲⽤于可见度测试。
这就是为什么变换到⼀个新的空间体中,⽽不是投影到⼀个平⾯上。
透视投影详解透视投影透视投影是⽤中⼼投影法将形体投射到投影⾯上,从⽽获得的⼀种较为接近视觉效果的单⾯投影图。
它具消失感、距离感、相同⼤⼩的形体呈现出有规律的变化等⼀系列的透视特性,能逼真地反映形体的空间形象。
透视投影也称为透视图,简称透视。
在建筑设计过程中,透视图常⽤来表达设计对象的外貌,帮助设计构思,研究和⽐较建筑物的空间造型和⽴⾯处理,是建筑设计中重要的辅助图样。
透视投影符合⼈们⼼理习惯,即离视点近的物体⼤,离视点远的物体⼩,远到极点即为消失,成为灭点。
它的视景体类似于⼀个顶部和底部都被切除掉的棱椎,也就是棱台。
这个投影通常⽤于动画、视觉仿真以及其它许多具有真实性反映的⽅⾯。
在平⾏投影中,图形沿平⾏线变换到投影⾯上;对透视投影,图形沿收敛于某⼀点的直线变换到投影⾯上,此点称为投影中⼼,相当于观察点,也称为视点。
平⾏投影和透视投影区别在于透视投影的投影中⼼到投影⾯之间的距离是有限的,⽽平⾏投影的投影中⼼到投影⾯之间的距离是⽆限的。
当投影中⼼在⽆限远时,投影线互相平⾏,所以定义平⾏投影时,给出投影线的⽅向就可以了,⽽定义透视投影时,需要指定投影中⼼的具体位置平⾏投影保持物体的有关⽐例不变,这是三维绘图中产⽣⽐例图画的⽅法。
物体的各个⾯的精确视图可以由平⾏投影得到。
另⼀⽅⾯,透视投影不保持相关⽐例,但能够⽣成真实感视图。
对同样⼤⼩的物体,离投影⾯较远的物体⽐离投影⾯较近物体的投影图象要⼩,产⽣近⼤远⼩的效果.透视投影的原理和实现by Goncely摘要:透视投影是3D渲染的基本概念,也是3D程序设计的基础。
掌握透视投影的原理对于深⼊理解其他3D渲染管线具有重要作⽤。
本⽂详细介绍了透视投影的原理和算法实现,包括透视投影的标准模型、⼀般模型和屏幕坐标变换等,并通过VC实现了⼀个演⽰程序。
1 概述在计算机三维图像中,投影可以看作是⼀种将三维坐标变换为⼆维坐标的⽅法,常⽤到的有正交投影和透视投影。
正交投影多⽤于三维健模,透视投影则由于和⼈的视觉系统相似,多⽤于在⼆维平⾯中对三维世界的呈现。
透视投影透视投影最显著的特征就是透视缩短,物体距离照相机越远,它在最终图像中看上去就越小。
这是因为透视投影的视景体可以看成是一个金字塔的平截头体(顶部被一个平行于底面的平面截除)。
位于视景体之内的物体被投影到金字塔的顶点,也就是照相机或观察点的位置。
靠近观察点的物体看上去更大一些,因为和远处的物体相比,它们占据了视景体中相对较大的区域。
这种投影方法常用于动画、视觉模拟以及其他要求某种程度的现实感的应用领域,因为它和我们在日常生活中观察事物的方式相同。
glFrustum()函数定义了一个平截头体,它计算一个用于实现透视投影的矩阵,并把它与当前的投影矩阵(一般为单位矩阵)相乘。
记住,视景体用于裁剪那些位于它之外的物体。
平截头体的4个侧面、顶面和底面对应于视景体的6个裁剪平面,如图3-13所示。
位于这些平面之外的物体(或物体的一部分)将裁剪掉,1.void glFrustum(GLdouble left, GLdouble right,2.GLdouble bottom, GLdouble top,3.GLdouble near, GLdouble far);创建一个表示透视视图平截头体的矩阵,并把它与当前矩阵相乘。
平截头体的视景体是由这个函数的参数定义的:(left, bottom, -near)和(right, top, -near)分别指定了近侧裁剪平面左上角和右下角的(x, y, z)坐标。
near和far分别表示从观察点到近侧和远侧裁剪平面的距离,它们的值都应该是正的。
平截头体在三维空间中有一个默认的方向。
可以在投影矩阵上执行旋转或移动,对这个方向进行修改。
但是,这种做法难度较大,因此最好还是避免。
高级话题平截头体并不一定要求是对称的,它的轴也并不需要与z 轴对齐。
例如,可以使用glFrustum()函数绘制一幅图片,就像透过房子右上角的一个矩阵窗口向外观察一样。
摄像师使用这种视景体创建人工透视效果。
和透视变换相关的参数
透视变换(Perspective Transformation)是一种将二维图像映射到三维空间中的变换方式,通常用于模拟人眼观察物体的视觉效果。
透视变换涉及到多个参数,以下是其中一些主要的参数:投影矩阵(Projection Matrix):投影矩阵定义了从三维空间到二维图像的映射关系。
它通常由四个参数组成,即焦距(f)、主点(h)、副点(v)和倾斜因子(k)。
这些参数共同决定了投影的方向和形状。
旋转矩阵(Rotation Matrix):旋转矩阵用于描述物体在三维空间中的旋转。
它通常由三个参数组成,即绕x轴、y轴和z轴的旋转角度。
这些参数可以单独调整,也可以组合使用以实现复杂的旋转效果。
平移矩阵(Translation Matrix):平移矩阵用于描述物体在三维空间中的平移。
它通常由三个参数组成,即沿x轴、y轴和z 轴的平移距离。
这些参数可以单独调整,也可以组合使用以实现复杂的平移效果。
缩放因子(Scaling Factor):缩放因子用于描述物体在三维空间中的缩放。
它通常由一个参数组成,即缩放因子的大小。
这个参数可以单独调整,也可以组合使用以实现复杂的缩放效果。
这些参数共同决定了透视变换的效果,可以根据具体需求进行调整和组合。
需要注意的是,透视变换通常需要结合其他图像
处理技术(如插值、滤波等)来实现更复杂的视觉效果。
OpenGL 入门纪录--2 .透视函数glFrustum(), gluPerspective()函数用法和glOrtho()函数用
法
2008-12-24 16:14
在OpenGL中,如果想对模型进行操作,就要对这个模型的状态(当前的矩阵)乘上这个操作对应的一个矩阵.
如果乘以变换矩阵(平移, 缩放, 旋转), 那相乘之后, 模型的位置被变换;
如果乘以投影矩阵(将3D物体投影到2D平面), 相乘后, 模型的投影方式被设置;
如果乘以纹理矩阵(), 模型的纹理方式被设置.
而用来指定乘以什么类型的矩阵, 就是glMatriMode(GLenum mode);
glMatrixMode有3种模式: GL_PROJECTION 投影, GL_MODELVIEW 模型视图, GL_TEXTURE 纹理.
所以,在操作投影矩阵以前,需要调用函数:
glMatrixMode(GL_PROJECTION); //将当前矩阵指定为投影矩阵
然后把矩阵设为单位矩阵:
glLoadIdentity();
然后调用glFrustum()或gluPerspective(),它们生成的矩阵会与当前的矩阵相乘,生成透视的效果;
1.glFrustum()
这个函数原型为:
void glFrustum(GLdouble left, GLdouble Right, GLdouble bottom, GLdouble top, GLdouble near, GLdouble far);
创建一个透视型的视景体。
其操作是创建一个透视投影的矩阵,并且用这个矩阵乘以当前矩阵。
这个函数的参数只义近裁剪平面的左下角点和右上角点的三维空间坐标,即(left,bottom,-near)和(right,top,-near);最后一个参数far是远裁剪平面的离视点的距离值,其左下角点和右上角点空间坐标由函数根据透视投影原理自动生成。
ne 和far表示离视点的远近,它们总为正值(near/far 必须>0)。
2.gluPerspective()
这个函数原型为:
void gluPerspective(GLdouble fovy,GLdouble aspect,GLdouble zNear, GLdouble zFar);
创建一个对称的透视型视景体,但它的参数定义于前面的不同,如图。
其操作是创建一个对称的透视投影矩阵,并且用这个矩阵以当前矩阵。
参数fovy定义视野在Y-Z平面的角度,范围是[0.0, 180.0];参数aspect是投影平面宽度与高度的比率;参数Near和F 分别是近远裁剪面到视点(沿Z负轴)的距离,它们总为正值。
以上两个函数缺省时,视点都在原点,视线沿Z轴指向负方向。
void mydisplay (void)
{
......
glMatrixMode (GL_PROJECTION);
LoadIdentity ();
Frustum (left, right, bottom, top, near, far);
......
}
3.glOrtho()
这个函数的原型为:
glOrtho(GLdouble left, GLdouble right, GLdouble bottom, GLdouble top, GLdouble near, GLdouble far)
六个参数, 前两个是x轴最小坐标和最大坐标,中间两个是y轴,最后两个是z轴值
它创建一个平行视景体(就是一个长方体空间区域)。
实际上这个函数的操作是创建一个正射投影矩阵,并且用这个矩阵乘以当前矩阵。
其中近裁剪平面是一个矩形,矩形左下角点三维空间坐标是(left,bottom,-near),
右上角点是(right,top,-near);远裁剪平面也是一个矩形,左下角点空间坐标是(left,bottom,-far),右上角点是(right,top,far)。
注意,所有的near和far值同时为正或同时为负, 值不能相同。
如果没有其他变换,正射投影的方向平行于Z轴,且视点朝向Z负轴。
这意味着物体在视点前面时far和near都为负值,物体在视点后面时far和near都为正值。
只有在视景体里的物体才能显示出来。
如果最后两个值是(0,0),也就是near和far值相同了,视景体深度没有了,整个视景体都被压成个平面了,就会显示不正确。