结构力学位移法的计算分享资料
- 格式:ppt
- 大小:2.56 MB
- 文档页数:17

第7章位移法一。
教学目的掌握位移法的基本概念;正确的判断位移法基本未知量的个数;熟悉等截面杆件的转角位移方程;熟练掌握用位移法计算荷载作用下的刚架的方法了解位移法基本体系与典型方程的物理概念和解法。
二。
主要章节§7—1 位移法的基本概念§7-2 杆件单元的形常数和载常数-位移法的前期工作§7—3 位移法解无侧移刚架§7-4 位移法解有侧移刚架§7-5 位移法的基本体系§7—6 对称结构的计算*§7—7支座位移和温度改变时的位移法分析(选学内容)§7-8小结§7—9思考与讨论三. 学习指导位移法解超静定结构的基础是确定结构的基本未知量以及各个杆件的转角位移方程,它不仅可以解超静定结构,同时还可以求解静定结构,另外,要注意杆端弯矩的正负号有新规定。
四。
参考资料《结构力学(Ⅰ)—基本教程第3版》P224~P257第六章我们学习了力法,力法和位移法是计算超静定结构的两个基本方法,力法发展较早,位移法稍晚一些。
力法把结构的多余力作为基本未知量,将超静定结构转变为将定结构,按照位移条件建立力法方程求解的;而我们今天开始学的这一章位移法则是以结构的某些位移作为未知量,先设法求出他们,在据以求出结构的内力和其他位移。
由位移法的基本原理可以衍生出其他几种在工程实际中应用十分普遍的计算方法,例如力矩分配法和迭代法等.因此学习本章内容,不仅为了掌握位移法的基本原理,还未以后学习其他的计算方法打下良好的基础。
此外,应用微机计算所用的直接刚度法也是由位移法而来的,所以本章的内容也是学习电算应用的一个基础。
本章讨论位移法的原理和应用位移法计算刚架,取刚架的结点位移做为基本未知量,由结点的平衡条件建立位移法方程.位移法方程有两种表现形式:①直接写平衡返程的形式(便于了解和计算)② 基本体系典型方程的形式(利于与力法及后面的计算机计算为基础的矩阵位移法相对比,加深理解)§7-1 位移法的基本概念1。
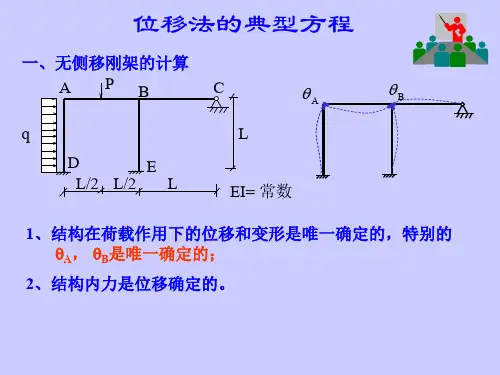

第8章 位移法(知识点小结)一、杆端内力正负号规定(图8-1)杆端弯矩AB M 、BA M :以绕杆端顺时针为正,逆时针为负;对结点或支座而言,截面弯矩以逆时针为正。
杆端剪力SAB F 、SBA F :以绕微段隔离体顺时针转动者为正,反之为负。
结点转角(杆端转角)A θ、B θ:顺时针转动为正。
两端垂直杆轴的相对线位移AB ∆:以使杆件顺时针转动为正,反之为负。
图8-1 杆端内力及杆端位移的正负号规定二、等截面直杆的转角位移方程—位移法计算的基础1、由杆端位移求杆端力——形常数考虑三种不同情况:两端固定直杆、一端固定另一端铰支的直杆及一端固定另一端滑动支承的直杆。
由杆端位移求杆端内力的公式(刚度方程),如表8-1所示,这里/i EI l =。
由杆端位移求出杆端弯矩后,杆端剪力可由平衡条件求出。
表8-1中,杆端内力是根据图示方向的位移方向求得的,当计算某一结构时,应根据其杆件所受的实际位移方向,判断其杆端内力的正负号及受拉侧。
2、由荷载求固定内力——载常数对三种等截面直杆,在荷载作用、温度改变作用下的杆端弯矩和剪力,称为固端弯矩和固端剪力(载常数)。
常见荷载作用下的载常数可查表所得。
3、等截面直杆的转角位移方程对等截面直杆,既有已知荷载作用,又有已知的杆端位移,可根据叠加原理,写出其杆端力的一般表达式,这即为等截面直杆的转角位移方程。
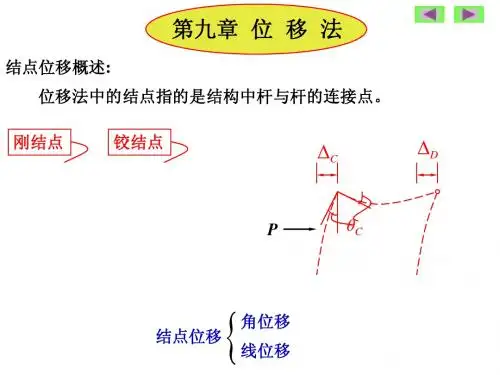
三、位移法的基本未知量包括独立的结点角位移和独立的结点线位移。
独立的结点角位移数目等于刚结点(包括组合结点、弹性抗转弹簧)的数目。
结点线位移的数目可通过增设支杆法(或铰化体系法)来确定。
铰化体系法就是将原结构中所有刚结点和固定支座均改为铰结点形成铰接体系,此铰接体系的自由度数就是原结构的独立结点线位移数。
然后分析该铰接体系的几何组成:如果它是几何不变的,说明结构无结点线位移;相反,如果铰接体系是几何可变的,再看最少需要增设几根附加支杆才能确保体系成为几何不变,或者说使此铰接体系成为几何不变而需添加的最少支杆数就等于原结构的独立结点线位移数目。

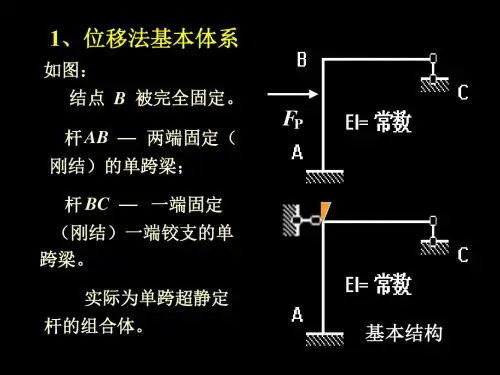

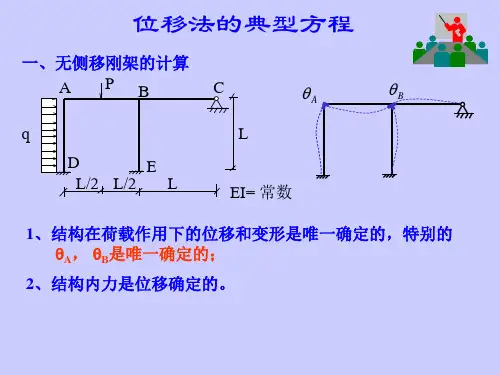



(2)位移互等定理: 据功的互等定理1·δ12=1·δ21 位移互等定理: 第二个单位力所引起的第一个单位力作用点沿其方向的位移,等于第一个单位力所引起的第二个单位力作用点沿其方向的位移。
即δ12= δ21 又如:ϕA 有↷ A C P1=1 B A C B ⌒ M=1 fC 36 ϕ A= f c(3)反力互等定理:据功的互等定理 1 △1=1 2 r12·△1= r21·△2 即 r21 1 2 △2=1 r12= r21 r12 上图表示支座1发生单位位移的状态,此时支座2产生的反力为r21。
下图表示支座2发生单位位移的状态,此时支座1产生的反力为r12。
反力互等定理:支座1发生单位位移所引起的支座2的反力,等于支座2发生单位位移所引起的支座1的反力。
37(4)反力位移互等定理由功的互等定理 r12ϕ1 + F2 Δ 21 = r22 i0 + rb i0 r12ϕ1 + F2 Δ 21 = 0 ϕ1 = 1, F2 = 1 可得r1 2 = − Δ 2 1 图a表示F2=1作用时,支座1的反力偶为r12,方向如图。
图b表示支座1顺r12方向发生单位转角时,F2作用点沿其方向的位移为△21。
反力位移互等定理:单位力所引起的结构某支座反力,等于该支座发生单位位移时 38 所引起的单位力作用点沿其方向的位移,符号相反。
主要内容一、图乘法的应用条件:二、图乘法的计算公式: ● 直杆 MMP 1 d s = ∑ (± A y 0 Δ = ∑∫ ● EI不变EI EI ● 至少有一个直线弯矩图三、图乘法的注意事项(1)必须符合上述三个前提条件;(2)竖标yC只能取自直线图形;(3)ω与yC若在杆件同侧则乘积取正号,反之取负号。
(4)顶点的切线与基线平行,才能用抛物线图形的面积和形心进行计算;反之,要把抛物线图形进行分解,应用叠加法求解. 互等定理适用于线弹性结构(包括静定结构和超静定结构) 39。