当前位置：文档之家 › 1.3 三种基本逻辑运算

1.3 三种基本逻辑运算

  • 格式：ppt
  • 大小：618.50 KB
  • 文档页数：11

下载文档原格式

  / 11

合集下载

1.3算术运算和逻辑运算

1.3算术运算和逻辑运算

1.3算术运算和逻辑运算1. 算术运算要点（1）移位操作①原码移位：原码进⾏算术左移和算术右移都不改变原码本⾝形态。

左移⼀位相当于乘以 2，右移⼀位相当于除以 2，移位出现的空位补0。

这是因为原码与⼆进制数真值的绝对值是完全⼀样的，算术移位并不涉及数的符号。

②补码移位：由于正数的补码与原码是⼀样的，所以正数的补码左、右移位所出现的空位补 0 均不会改变补码的形态。

值得注意的是负数补码的移位，当负数的补码右移时所出现的空位必须补 1 才能保证数值的正确及形体的保持。

③反码移位：由于正数的反码与原码相同，所以正数的反码左移⼀位相当于乘以2，左移出现的空位补 0，右移⼀位相当于除以 2，右移出现的空位补 0。

负数的反码左移⼀位相当于乘以 2，右移⼀位相当于除以 2，但左、右移位出现的空位必须补 1。

（2）不同编码下的规格化数浮点数是由数的阶码和数的尾数构成的。

令数的尾数为，则浮点规格化数的标准为。

规格化数的这⼀要求是从尾数的真值划定的标准，即要求尾数的绝对值⼤于或等于（相当于⼆进制数的）。

正数的规格化数⽆论是哪种编码，其尾数的最⾼位均为 1；负数的规格化数除原码外，其他编码尾数的最⾼位均为 0。

（3）溢出判断定点运算、浮点运算都会遇到溢出的问题，这是因为计算机中的运算是在⼀个有限制的空间进⾏的，当运算结果出现⼤于空间所允许的最⼤值时，则会出现上溢溢出；当运算结果出现⼩于空间所允许的最⼩值时，则会出现下溢溢出。

计算机把引起上溢溢出的值称为机器⽆穷⼤，把引起下溢溢出的值称为机器零。

浮点数是由阶和尾数构成的，浮点运算的溢出与否是由结果的阶来决定的，当运算结果的阶出现⼤于或⼩于计算机所容许的最⼤、最⼩值时，则会发⽣上溢或下溢溢出。

由于浮点数的阶是⼀个定点正数，且为 2 的指数，所以判定浮点运算可由阶所表⽰的量值给出。

定点加法、减法采⽤补码求和的运算⽅法，判断运算中的溢出有两种办法：⼀种是利⽤进位值，另⼀种是利⽤符号状态。

数字电路逻辑设计(第二版)清华大学出版社朱正伟等编著ch1综述

数字电路逻辑设计(第二版)清华大学出版社朱正伟等编著ch1综述
in1
4. 十六进制
十六进制数中只有0, 1, 2, 3, 4, 5, 6, 7, 8, 9 , A、B、C、D、E、 F十六个数码，进位规律是“逢十六进一”。各位的权均为16 的幂。
例如 (A6.C) 10 161 6 160 12 161 H
一般表达式：
m
S16 ai 16i
1.数字逻辑基础
1.1 数字电路概述 1.2 数制与码制 1.3逻辑代数的运算 1.4逻辑代数的基本定律和基本运算规则
1.5逻辑函数的表示方法及标准形式 1.6逻辑函数的化简
1.1 数字电路概述
1.1.1模拟信号与数字信号
1. 模拟信号 ---时间和数值均连续变化的电信号，如正弦波、三角波等
u
O
t
3.数字电路的分析、设计与测试
(1)数字电路的分析方法 数字电路的分析:根据电路确定电路输出与输入之间的逻辑关系。 分析工具：逻辑代数。 电路逻辑功能主要用真值表、功能表、逻辑表达式和波形图。
(2) 数字电路的设计方法
数字电路的设计:从给定的逻辑功能要求出发，选择适当的逻辑 器件，设计出符合要求的逻辑电路。 设计方式:分为传统的设计方式和基于EDA软件的设计方式。 (3) 数字电路的测试方法
1.1.2 数字电路
1..数字集成电路的分类
（3）按所采用的半导体类型分类 --数字集成电路可分为双极型电路 和单极型电路 。
a.双极型电路 --采用双极型半导体器件作为元件。双极型电 路可分为：TTL电路、ECL 电路和I２L 等类型。
b.单极型电路--采用金属-氧化物半导体场效应管(简称为 MOS管)作为元件。 MOS集成电路又可分为PMOS、 NMOS和CMOS等类型。
2 37 …………… 余 …… b0

新《数字电子技术》课程标准

新《数字电子技术》课程标准

《数字电子技术》课程标准一、概述（一）课程性质本课程是五年制高职应用电子专业的专业主干项目课程。

通过本课程的学习，使学生掌握数字电路的相关理论，使学生具备高职应用型人才所必须的常用数字集成电路的应用能力，掌握常见仪器、仪表的使用，熟悉简单电子产品的一般设计过程，数字集成电路制作与调试，培养学生独立分析问题和解决问题的能力，训练学生的创新能力。

本课程是《模拟电子设计与制作》的后续课程。

是《单片机原理及应用》、《PLC及其应用技术》、《集成电路应用技术》等课程的前修基础课程。

（二）课程基本理念本课程标准的基本理念：用项目课程，突出专业课程的实践性、针对性和实用性，努力实现课程功能取向与人才培养目标取向一致性。

以强化应用为重点，以就业为导向，以能力为本位，加强实践性教学环节，注重学生综合职业素质的提高。

紧紧围绕完成工作任务的需要来选择课程内容，改变传统的学科体系中理论的“难、繁、旧、偏”等状况，增加与就业岗位直接相关的新知识、新技术和新工艺。

以“工作项目”为主线，变学科体系本位为职业能力本位，变书本知识的传授为技能的训练，结合职业资格鉴定，培养学生的实践动手能力。

实现专业课程内容与职业岗位（群）、工作任务和工作过程相一致，实现专业教育与职业资格证书相融合。

（三）课程设计思路1、按照“以能力为本位，以职业实践为主线，以项目课程为主体的模块化专业课程体系”的总体设计要求，该门课程以形成具有灵活应用常用数字集成电路实现逻辑功能的能力为基本目标，彻底打破学科课程的设计思路，紧紧围绕工作任务完成的需要来选择和组织课程内容，突出工作任务与知识的联系，让学生在职业实践活动的基础上掌握知识，增强课程内容与职业岗位能力要求的相关性，提高学生的就业能力。

2、学习项目选取的基本依据是该门课程涉及的工作领域和工作任务范围，但在具体设计过程中，还根据三人表决器或裁判器、抢答器和数字钟等典型产品为载体，使工作任务具体化，产生了具体的学习项目。

逻辑运算

逻辑运算

逻辑运算逻辑运算又称布尔运算布尔用数学方法研究逻辑问题，成功地建立了逻辑演算。

他用等式表示判断，把推理看作等式的变换。

这种变换的有效性不依赖人们对符号的解释，只依赖于符号的组合规律。

这一逻辑理论人们常称它为布尔代数。

20世纪30年代，逻辑代数在电路系统上获得应用，随后，由于电子技术与计算机的发展，出现各种复杂的大系统，它们的变换规律也遵守布尔所揭示的规律。

逻辑运算(logical operators) 通常用来测试真假值。

最常见到的逻辑运算就是循环的处理，用来判断是否该离开循环或继续执行循环内的指令。

目录1基本概念2表示方法3运算符号4运算规则1 4.1 逻辑加法1 4.2 逻辑乘法1 4.3 逻辑否定1 4.4 异或运算1基本概念1.逻辑常量与变量：逻辑常量只有两个，即0和1，用来表示两个对立的逻辑状态。

逻辑变量与普通代数一样，也可以用字母、符号、数字及其组合来表示，但它们之间有着本质区别，因为逻辑变量的取值只有两个，即0和1，而没有中间值。

2.逻辑运算：在逻辑代数中，有与、或、非三种基本逻辑运算。

表示逻辑运算的方法有多种，如语句描述、逻辑代数式、真值表、卡诺图等。

3.逻辑函数：逻辑函数是由逻辑变量、常量通过运算符连接起来的代数式。

同样，逻辑函数也可以用表格和图形的形式表示。

4.逻辑代数：逻辑代数是研究逻辑函数运算和化简的一种数学系统。

逻辑函数的运算和化简是数字电路课程的基础，也是数字电路分析和设计的关键。

2表示方法"∨" 表示"或" （逻辑加法）"∧" 表示"与". （逻辑乘法）"┐"表示"非". （逻辑否定）"=" 表示"等价".1和0表示"真"和"假"(还有一种表示,"+"表示"或", "·"表示"与")3运算符号各种编程语言中的逻辑运算符4运算规则A......B..................A And B....A Or B........A Xor B0......0.......................0..............0. 01......0.......................0..............1. (1)0......1.......................0..............1. (1)1......1.......................1..............1. 0简单的说And:与运算。

三种基本逻辑运算

三种基本逻辑运算

L ≥1
.
A
A
≥1
B
B
L
C
C (a)
L (b)
或逻辑运算的基本规则为：
0 + 0 = 0，0 + 1=1，1 + 0= 1，1 + 1=1。
.
1.3.3 逻辑非运算 NOT 非逻辑：
一件事的发生是以其相反的条件为依据的。
电路图
电源
A
灯
L
语句描述
开关A 灯L 断开 亮 闭合 熄灭
表格描述 表达式
AL 01 10
.
电路图
A
B
电源
灯
L
语句描述
开关
A 断开 断开 闭合 闭合
开关
B 断开 闭合 断开 闭合
灯
L 熄灭 熄灭 熄灭 亮
表格描述 表达式
逻辑符号
AB L
00 0 01 0 10 0
L= A ·B A B
11 1
L &
.
A
B
A& B
Y
(a)
Y (b)
与逻辑运算的基本规则为：
0·0=0，0·1=0，1·0=0，1·1=1
1.3 三种基本逻辑运算
逻辑代数 ： 按一定的逻辑规律进行运算的代数。用
字母表示变量，但变量取值仅有0、1两种值，0、1不表示数 值的大小，而表示两种对立的逻辑状态。
逻辑代数定义了3中基本逻辑运算：与 、或、非
1.3.1 逻辑与运算 AND 与逻辑：
只有当一件事的几个条件全部具备之后， 这件事才能发生。
• 与、或、非运算的运算规则 • 门符号的识别 • 真值表描述 • 逻辑表达式描述 • 简单的输入输出波形分析

数电简明教程第一章 逻辑代数基础知识

数电简明教程第一章 逻辑代数基础知识

10
第六章 脉冲产生与整形电路
概述 6.1 施密特触发器
11
12
概 述
一、逻辑代数（布尔代数、开关代数） 逻辑： 事物因果关系的规律 逻辑函数: 逻辑自变量和逻辑结果的关系
Z f ( A, B, C )
逻辑变量取值：0、1 分别代表两种对立的状态 一种状态 另一状态 高电平 真 低电平 假 是 非 有 无 … … 1 0 0 1
概述 3.1 3.2 3.3 3.4 3.5 组合电路的分析方法和设计方法 加法器和数值比较器 编码器和译码器 数据选择器和分配器 用 MSI 实现组合逻辑函数
8
第四章
概述
触发器
4.1 基本触发器 4.2 同步触发器 4.3 边沿触发器 4.4 触发器的电气特性
9
第五章
时序逻辑电路
概述 5.1 时序电路的基本分析和设计方法 5.2 计数器 5.3 寄存器和读/写存储器
( 26 )10 = 16 + 8 + 2 = 24 +23 + 21 = ( 1 1 0 1 0 )2
16 8 4 2 1
20
(3) 二-八转换: 每 3 位二进制数相当一位 8 进制数
( 0 10 101 111 ) 2 ( 257 )8
2 5 7
( 0 1 0 0 1 1 1 0 0 0 0 1. 0 0 0 1 1 0 )2 ( 2 3 4 1 . 0 6 )8
(4) 八-二转换: 每位 8 进制数转换为相应 3 位二进制数
( 31. 47 )8 ( 011 001 . 100 111
)2
)2
( 375.64 )8 ( 011 111 101 . 110 100

数电第二讲 基本公式 基本定律及应用

数电第二讲 基本公式 基本定律及应用

例： A• B= A+B • 得
ABC = A + BC = A + B + C
由此反演律能推广到n个变量： 由此反演律能推广到n个变量：
A 1 • A 2 • … • A n = A1 + A 2 + … + A n A 1 + A 2 + … + A n = A1 • A 2 • … • A n
或非： 或非：条件
A、B、C任一 、 、 任一 具备， 具备，则F 不 发生。 发生。
F = A+B+C
A B C
≥1
F
异或：条件A、 异或：条件 、
B有一个具备， B有一个具备， 有一个具备 另一个不具备 发生。 则F 发生。
F= A ⊕ B ⊕C
A B C A B C
=1
F
同或： 同或：条件
A、B相同，则 、 相同 相同， F 发生。 发生。
§1.３ 基本逻辑运算 1.３
逻辑变量 取值： 逻辑0 逻辑1 逻辑0 和逻辑1 取值 ： 逻辑 0 、 逻辑 1 。 逻辑 0 和逻辑 1 不代表数值大小 仅表示相互矛盾、 数值大小， 不代表 数值大小 ， 仅表示相互矛盾 、 相互 对立的两种逻辑状态． 对立的两种逻辑状态． 两种逻辑状态 基本逻辑运算 与运算 或运算 非运算
AB + A C + BC = AB + AC + (A + A )BC
= AB(1 + C) + AC(1 + B)
= AB + AC =
等式右边
由此可以看出：与或表达式中，两个乘积项分别包 由此可以看出： 与或表达式中， 同一因子的 变量和反变量， 含同一因子的原变量和反变量，而两项的剩余因子 包含在第三个乘积项中， 包含在第三个乘积项中，则第三项是多余的 公式可推广： 公式可推广： AB + AC + BCDE = AB + AC

逻辑代数中的三种基本运算

逻辑代数中的三种基本运算

& ≥1
Y3
(真值表略)
(4) 异或逻辑 A
=1
(Exclusive—OR) B
Y4 A B AB AB
(5) 同或逻辑 (异或非)
(Exclusive—NOR)
Y5 A B
A B
=1
AB AB
= A⊙B
Y4
A B Y4 00 0
01 1
10 1
11 0
A B Y5
) A
公式 (4) 证明： AB AC BC AB AC
左 AB AC ( A A) BC A AB A AB AC ABC ABC AB AC
推论
AB AC BCD AB AC
公式 (5) 证明： AB AB A B AB
左 AB AB ( A B) ( A B)
A A A B AB B B A B AB 即 A B = A⊙B 同理可证 A⊙B A B
六、关于异或运算的一些公式
异或 A B AB AB A B = A⊙B 同或 A⊙B AB A B A⊙B A B (1) 交换律 A B B A
(2) 结合律 ( A B) C A ( B C ) (3) 分配律 A ( B C) AB AC
(4) 常量和变量的异或运算 A 1 A A 0 A
(5) 因果互换律
如果 A B C
A A 0 A A 1
则有 A C B BC A
电源
开关B
灯Y
逻
或逻辑关系
辑A 符B
≥1
Y
号
或门（OR gate)

数字电子技术基础7 与、或、非(基本逻辑运算)1.3.1.1 与、或、非

数字电子技术基础7 与、或、非(基本逻辑运算)1.3.1.1 与、或、非
数字电子技术基础
7. 与、或、非（基本逻辑运算）
主讲人：杨聪锟
1. 问题的引入
数制与码制 常用的逻辑运算
逻辑门电路 布尔代数（逻辑代数基础）
1. 问题的引入
常用的 逻辑运算
与
或
基本逻辑运算
非
常用复合逻辑 同或
异或
与非 或非 与或非
2. 逻辑“与”
当一个逻辑命题的所有条件（输入）同时成立时，
结论（输出）才成立。
AB F
F A B AB
00 0 01 0 10 0 11 1
A &F B 矩形轮廓符号
A
B
F
特定外形符号
A FB 曾用符号源自2. 逻辑“或”一个逻辑命题的所有条件（输入）中，只要有一个
成立，结论（输出）就成立。 A B F
F A B
00 0 01 1 10 1 11 1
A ≥1 F B 矩形轮廓符号
A B
F
特定外形符号
A F
B 曾用符号
2. 逻辑“非”
逻辑命题的条件不成立时，结论必成立； 条件成立时，结论必不成立，
简言之，结论是条件的否定。
F A F A
AF
01 10
A1
FA
FA
F
矩形轮廓符号 特定外形符号
曾用符号

基本逻辑运算

基本逻辑运算

2.3.1 TTL与非门的基本结构及工作原理
+VCC（ + 5V） R 3kΩ
D
Rc 1kΩ
D5 3 1
A B C
1
P
D
4
L
T 2
D2 D 3
R1 4.7kΩ
+VCC （ + 5V ） Rb1
+VCC （ +5V） R b1
A B C
N N N
P P P
P
N
1
3
A B C
T1
1. 电路基本结构
+V CC （ + 5V） Rc 2 R b1 4kΩ
1.输入低电平电流IIL——是指当门电路的输入端接低电平时，从 门电路输入端流出的电流。
可以算出：
I IL
VCC VB1 5 1 1(mA) Rb1 4
产品规定IIL＜1.6mA。
2.输入高电平电流IIH ——是指当门电路的输入端接高电平时，流入 输入端的电流。
产品规定：IIH＜40uA。
3 主要参数
（1)TTL与非门提高工作速度的原理
a.采用多发射极三极管加快了存储电荷的消散过程。
+VCC Rc 2 i B1 1V R b1 4kΩ
1
1.6kΩ
3.6V A B C 0.3V
3
1.4V
1
3
T1 β iB1 0.7V
T2 2
3 1
Vo T3 2
Re 2 1kΩ
b.采用了推拉式输出级，输出阻抗比较小，可迅速给负载电容充放电。
2.1
一、基本逻辑运算 1．与运算
设：开关闭合=―1‖ 开关不闭合=―0‖

数字逻辑电路基础

数字逻辑电路基础
用四位自然二进制码中的前十个码字来表示十进 制数码，因各位的权值依次为8、4、2、1，故称8421 BCD 码。
常用 BCD 码
十进制数 8421 码 余 3 码 格雷码 2421 码
0
0000 0011 0000 0000
1
0001 0100 0001 0001
2
0010 0101 0011 0010
数字逻辑电路基础
第一章 数字逻辑电路基础
1.1 数字电路的基本概念 1.2 数制和码制 1.3 基本逻辑运算 1.4 逻辑函数的表示方法 1.5 逻辑代数运算 1.6 逻辑门电路
1.1 数字电路基本概念
一、模拟信号与数字信号
模拟信号——时间连续数值也连续的信号。如速度、压 力、温度等。 数字信号——在时间上和数值上均是离散的。如电子表 的秒信号，生产线上记录零件个数的记数信号等。 数字信号在电路中常表现为突变的电压或电流。
晶体管工作在开关状 态
1、数字信号的特点
•使用高低电平来表示信号。 •门电路起开关作用。 •逻辑状态只有0，1。 •易于存储。 •抗干扰，对元件的要求不高。 •集成度高，通用性强。
2、用逻辑电平描述的数字波形：
数字波形
逻辑电平对时间的图形表示。 脉冲波： 当某波形仅有两个离散值时。 分为：周期波和非周期波
即：(1234)10＝1×103 ＋2×102＋3×101＋4×100
又如：(209.04)10＝ 2×102 ＋0×101＋9×100＋0×10－1＋4 ×10－
2、二进制
数码为：0、1；基数是2。 运算规律：逢二进一，即：1＋1＝10。 二进制数的权展开式： 如：(101.01)2＝ 1×22 ＋0×21＋1×20＋0×2－1＋1 ×2

逻辑代数

逻辑代数

For personal use only in study and research; not forcommercial use逻辑代数逻辑代数是一种描述客观事物逻辑关系的数学方法，是英国数学家乔治.布尔（George Boole）于1847年首先提出来的，所以又称布尔代数。

由于逻辑代数中的变量和常量都只有“0”和“1”两个取值，又可以称为二值代数。

逻辑代数是研究数字电路的数学工具，是分析和设计逻辑电路的理论基础。

逻辑代数研究的内容是逻辑函数与逻辑变量之间的关系。

1.3.1逻辑代数中的三种基本逻辑关系1．逻辑代数中的几个问题（1）逻辑代数中的变量和常量逻辑代数与普通代数相似，有变量也有常量。

逻辑代数中的变量用大写英文字母A、B、C…表示，称为逻辑变量。

每个逻辑变量的取值只有“0”和“1”两种。

逻辑代数中的常量，只有两个“0”和“1”。

与普通代数不同的是这里的“0”和“1”不再表示数值的大小，而是代表两种不同的逻辑状态。

例如可以用“1”和“0”表示开关的“闭合”与“断开”；信号的“有”和“无”；“高电平”与“低电平”；“是”与“非”等。

究竟代表什么意义，要视具体情况而定。

（2）正逻辑和负逻辑的规定脉冲信号的高、低电平可以用“1”和“0”来表示。

规定：如果高电平用“1”表示，低电平用“0”表示，则称这种表示方法为正逻辑。

如果高电平用“0”表示，低电平用“1”表示，则称这种表示方法为负逻辑。

以后如果无特殊声明，均采用正逻辑2．基本逻辑关系逻辑代数中有与、或、非三种基本逻辑关系，分别对应着与、或、非三种基本逻辑运算。

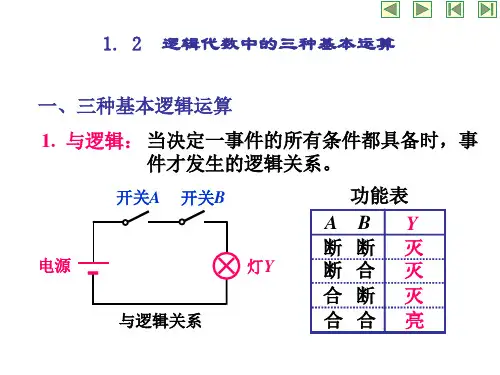
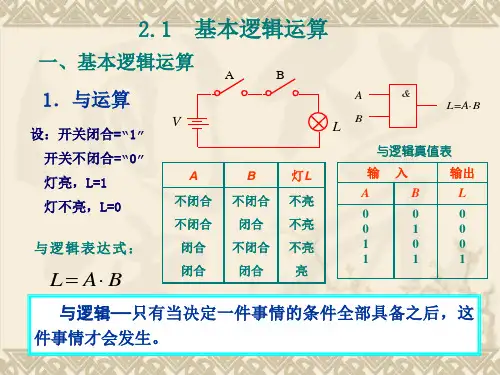
（1）“与”逻辑如图1-5（a）所示的串联开关电路中，把“开关闭合”作为条件，把“灯亮”这件事情作为结果，那么图1-5（a）说明：只有决定某件事情的所有条件都具备时，结果才会发生。

这种结果与条件之间的关系称为“与”逻辑关系，简称“与”逻辑。

图1-5（b）是“与”逻辑的逻辑符号。

图1-5 “与”逻辑与运算符号为“?”，与逻辑用表达式可以表示为Y = A·B或写成 Y＝AB（省略运算符号）。

第一章 逻辑代数基础

第一章 逻辑代数基础
V(v)
t
典型模拟信号
1.1.2 数制和码制 1.1.2数制和码制
一、数制
多位数码中每一位的构成方法以及从低位 到高位的进位规则 • 十进制 Decimal system( 逢十进一） 码：0，1，2，3，4，5，6，7，8，9 基：10 权： 10i i D = k × 10 表达式： ∑i
(143.75)10 = 1×10 2 + 4 ×101 + 3 ×100 + 7 ×10 −1 + 5 ×10−2
1 = 0， 0 =1
1+A=1 0+A=A A+A=A A+ Ā=1 A+B=B+A A+(B+C)=(A+B)+C A+B •C=(A+B) •(A+C) 重叠律 互补律 交换律 结合律 分配律 反演律 还原律
A⋅ B = A+ B
A + B = A⋅ B
1.3.2若干常用公式
序号 21 22 23 24 25 26 公式 A + A·B = A A + Ā·B = A + B
A B
Y
0 1 1 1
�Y
E
0 0 1 1
0 1 0 1
或逻辑表达式为： Y=A+B A 或运算由与逻辑门电路实现，其逻辑符号为： B
≥1
Y
• 非运算：只要条件具备了，结果就不会发生；而条
件不具备时；结果就发生。 例：设1表示开关闭合或灯亮；0表示开关不闭合或灯不亮
R A Y A
�Y
0 1 1 0
编码种类 十进制数 0 1 2 3 4 5 6 7 8 9 权 8421码 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 8421 余3码 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 2421码 0000 0001 0010 0011 0100 1011 1100 1101 1110 1111 2421 5211码 0000 0001 0100 0101 0111 1000 1001 1100 1101 1111 5211 余3循环码 0010 0110 0111 0101 0100 1100 1101 1111 1110 1010

1.3逻辑代数基础

1.3逻辑代数基础
1.3 逻辑代数基础
逻辑代数是按一定的逻辑关系进行运算的代数，是分 析和设计数字电路的数学工具。在逻辑代数，只有０和１ 两种逻辑值，有与、或、非三种基本逻辑运算，还有与或、 与非、与或非、异或几种导出逻辑运算。 逻辑是指事物的因果关系，或者说条件和结果的关系， 这些因果关系可以用逻辑运算来表示，也就是用逻辑代数 来描述。 事物往往存在两种对立的状态，在逻辑代数中可以抽 象地表示为 0 和 1 ，称为逻辑0状态和逻辑1状态。 逻辑代数中的变量称为逻辑变量，一般用大写字母 表示。逻辑变量的取值只有两种，即逻辑0和逻辑1，0 和 1 称为逻辑常量，并不表示数量的大小，而是表示两种对 立的逻辑状态。
A E B Y
A接通、B断开，灯不亮。
A、B都接通，灯亮。
两个开关必须同时接通， 灯才亮。逻辑表达式为：
Ｙ＝ＡＢ
功能表
开关 A 开关 B 断开 断开 闭合 闭合 断开 闭合 断开 闭合 灯Y 灭 灭 灭 亮
将开关接通记作1，断开记作0； 灯亮记作1，灯灭记作0。可以作 出如下表格来描述与逻辑关系：
A B
0-1率A· 1=1
冗余律： AB A C BC AB A C
证明： AB A C BC
AB A C ( A A) BC
AB A C ABC A BC
互补率A+A=1 分配率 A(B+C)=AB+AC 0-1率A+1=1
AB(1 C) A C(1 B)
=1
Y
A B
异或门的逻辑符号
L=A+B （4） 与或非运算：逻辑表达式为： Y AB CD
A B C D & ≥1 Y
A B C D & ≥1 & 与或非门的等效电路 Y

数字电子技术基础电子教案(周良权)

数字电子技术基础电子教案(周良权)

A B Y 逻辑表达式 开关 A 开关 B 灯 Y 规定: 0 开关闭合为逻辑 0 0 1 Y=A ·B 或 断 Y = AB灭 断 0 断开为逻辑 1 0 0 断 合 灭 灯亮为逻辑 1 1 0 0 合 断 与门 灭 灯灭为逻辑 0 开关 1 A、 1 B 都闭合时， 1 合 合 (AND 亮 gate) 灯 Y 真值表 才亮。 若有 0 出 0；若全 1 出 1
若相同出 1 若相异出 0
数 字 电 路 基 础
1.5逻辑函数的几种表示方法及其相互转换
主要要求： 1、已知真值表求逻辑表达式和逻辑图。 2、已知逻辑函数式求真值表和逻辑图。 3、已知逻辑图求逻辑函数式和真值表。
数 字 电 路 基 础
根据真值表求函数表达式的方法是：
将真值表中每一组使输出函数值为1的输入变量都写成一 个乘积项。在这些乘积项中，取值为1的变量，则该因子写成 原变量，取值为0的变量，则该因子写成反变量，将这些乘积 项相加，就得到了逻辑函数式。
第1章数字电路基础
概述 几种常用的数制和码制 逻辑函数中三种最基本的逻辑运算 复合逻辑函数 逻辑函数的几种表示方法及其相互转换 逻辑代数 逻辑函数的卡诺图化简法 关于正逻辑和负逻辑的规定及其转换
数 字 电 路 基 础
本章教学基本要求
1、数制和码制，各种数制间的转换；
2、与、或、非逻辑和其它复合逻辑函数；
有 8421 码 5421 码 0000 0000 0001 0001 0010 0010 0011 0011 0100 0100 0101 1000 0110 1001 0111 1010 1000 1011 1001 1100
权 码 2421(A) 2421(B) 0000 0000 0001 0001 0010 0010 0011 0011 0100 0100 0101 1011 0110 1100 0111 1101 1110 1110 1111 1111

数字电子技术基础第三版第一章答案

数字电子技术基础第三版第一章答案

第一章数字逻辑基础第一节重点与难点一、重点：1.数制2。

编码（1) 二-十进制码（BCD码）在这种编码中,用四位二进制数表示十进制数中的0~9十个数码。

常用的编码有8421BCD码、5421BCD码和余3码。

8421BCD码是由四位二进制数0000到1111十六种组合中前十种组合，即0000～1001来代表十进制数0～9十个数码，每位二进制码具有固定的权值8、4、2、1,称有权码.余3码是由8421BCD码加3(0011）得来,是一种无权码。

(2）格雷码格雷码是一种常见的无权码.这种码的特点是相邻的两个码组之间仅有一位不同，因而其可靠性较高，广泛应用于计数和数字系统的输入、输出等场合。

3。

逻辑代数基础（1)逻辑代数的基本公式与基本规则逻辑代数的基本公式反映了二值逻辑的基本思想，是逻辑运算的重要工具,也是学习数字电路的必备基础.逻辑代数有三个基本规则，利用代入规则、反演规则和对偶规则使逻辑函数的公式数目倍增.(2）逻辑问题的描述逻辑问题的描述可用真值表、函数式、逻辑图、卡诺图和时序图,它们各具特点又相互关联，可按需选用。

（3）图形法化简逻辑函数图形法比较适合于具有三、四变量的逻辑函数的简化.二、难点：1。

给定逻辑函数，将逻辑函数化为最简用代数法化简逻辑函数，要求熟练掌握逻辑代数的基本公式和规则，熟练运用四个基本方法—并项法、消项法、消元法及配项法对逻辑函数进行化简.用图形法化简逻辑函数时,一定要注意卡诺图的循环邻接的特点，画包围圈时应把每个包围圈尽可能画大。

2。

卡诺图的灵活应用卡诺图除用于简化函数外，还可以用来检验化简结果是否最简、判断函数间的关系、求函数的反函数和逻辑运算等。

3。

电路的设计在工程实际中，往往给出逻辑命题，如何正确分析命题，设计出逻辑电路呢？通常的步骤如下：1．根据命题,列出反映逻辑命题的真值表； 2．根据真值表，写出逻辑表达式； 3．对逻辑表达式进行变换化简; 4．最后按工程要求画出逻辑图。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

L
A B C (a) L (b)
或逻辑运算的基本规则为：
A B C
≥1
L
0 + 0 = 0，0 + 1=1，1 + 0= 1，1 + 1=1。
1.3.3
逻辑非运算
NOT
非逻辑：
一件事的发生是以其相反的条件为依据的。
电路图 电源 A 灯 L
语句描述 开关A 灯L 断开 亮 闭合 熄灭
表格描述 A 0 1 L 1 0
电路图
A
B 灯 L
电源
语句描述
表格描述
合
开关 B 断开 闭合 断开 闭合
灯 L 熄灭 熄灭 熄灭 亮
AB 00 01 10 11
L 0 0 0 1
L= A · B
A
B
&
L
A B (a)
A B
&
Y
Y (b)
与逻辑运算的基本规则为：
0· 0=0，0· 1=0，1· 0=0，1· 1=1
1.3
三种基本逻辑运算
逻辑代数 ： 按一定的逻辑规律进行运算的代数。用
字母表示变量，但变量取值仅有0、1两种值，0、1不表示数 值的大小，而表示两种对立的逻辑状态。 逻辑代数定义了3中基本逻辑运算：与 1.3.1 逻辑与运算 AND
、或、非
与逻辑：
只有当一件事的几个条件全部具备之后，
这件事才能发生。
表达式
逻辑符号 L
L= A
A
1
1.3.4
基本运算的推广
表达式 与非运算
L= AB
逻辑符号
A B & L
或非运算 L= A+B
A
≥1
L
B A
B L
异或运算
L= A B+A B
=1
基本逻辑运算分析举例 1 A 0 1 0
B
1
L =AB 0
1 A B 0
1 0
L =A+B
1 0 1
A A
0
应掌握的内容
1.3.2
逻辑或运算
OR
或逻辑：
当一件事的几个条件只要有一个条件满足，
这件事就会发生。
电路图
A B 电源 灯 L
语句描述
表格描述
表达式
逻辑符号
开关 A 断开 断开 闭合 闭合
开关 B 断开 闭合 断开 闭合
灯 L 熄灭 亮 亮 亮
AB 00 01 10 11
L 0 1 1 1
L= A +B
A
B
≥1
• • • • •
与、或、非运算的运算规则 门符号的识别 真值表描述 逻辑表达式描述 简单的输入输出波形分析