基本逻辑运算

三种基本的逻辑运算关系逻辑运算是思维和推理过程中的基本工具，它帮助我们分析和理解事物之间的关系，从而得出合乎逻辑的结论。

在逻辑学中，有三种基本的逻辑运算关系，即合取、析取和否定。

本文将生动、全面地介绍这三种逻辑运算关系，并探讨它们在日常生活中的重要性和指导意义。

首先，我们来讨论合取。

合取是指将两个或多个命题连接起来，只有当全部命题都为真时，合取命题才为真。

这种关系可以用中文词语“且”来表示，例如“我喜欢吃水果且喜欢吃蔬菜”。

这个例子中，只有当我既喜欢吃水果又喜欢吃蔬菜时，这个合取命题才为真。

在日常生活中，合取关系经常用于描述人们的偏好、条件或要求。

它帮助我们对事物进行分类、评估和理解，从而做出合理的决策。

其次，我们来讨论析取。

析取是将两个或多个命题连接起来，只要其中至少一个命题为真，析取命题就为真。

这种关系可以用中文词语“或”来表示，例如“明天我要去看电影或去逛街”。

这个例子中，只要我选择去看电影或去逛街中的一个选项，这个析取命题就为真。

在日常生活中，析取关系经常用于描述选择、可能性或机会。

它帮助我们在不同选项之间做出决策，灵活应对各种情况。

最后，我们来讨论否定。

否定是将一个命题的真值取反，即真变为假，假变为真。

这种关系可以用中文词语“不”来表示，例如“我不喜欢吃辣”。

这个例子中，我对吃辣这个命题进行了否定，即我不喜欢吃辣。

在日常生活中，否定关系经常用于表达不同观点、意见或态度。

它帮助我们更加清晰地表达自己的立场，增加沟通的准确性和效果。

通过了解和运用合取、析取和否定这三种基本的逻辑运算关系，我们能够更好地思考和分析问题，做出明智的决策。

在学习和工作中，逻辑思维能力是至关重要的。

它帮助我们分析信息、理清思路、解决问题，并在日常生活中做出明智的选择。

逻辑思维是培养创新、提高效率和提升能力的关键技能。

因此，我们应该不断学习和掌握逻辑运算关系，运用它们来推理和分析，以求在各个领域取得成功。

四种基本逻辑运算一、与运算与运算是逻辑运算中的一种基本运算，也称为“与”操作。

与运算的结果只有在所有输入变量都为真（即为1）时才为真，否则为假（即为0）。

与运算的运算符通常用符号“∧”或“&”表示。

例如，对于两个输入变量A和B，A∧B表示A和B的与运算结果。

与运算在实际生活中的应用非常广泛。

例如，在某些情况下，我们需要判断多个条件是否同时满足，只有当所有条件都满足时，我们才能得出最终的结论。

这时，我们可以使用与运算来判断这些条件是否同时成立。

二、或运算或运算是逻辑运算中的另一种基本运算，也称为“或”操作。

或运算的结果只要有一个输入变量为真（即为1），就为真，否则为假（即为0）。

或运算的运算符通常用符号“∨”或“|”表示。

例如，对于两个输入变量A和B，A∨B表示A和B的或运算结果。

或运算在实际生活中也有广泛的应用。

例如，当我们需要判断多个条件中是否有一个满足时，只要有一个条件满足，我们就可以得出最终的结论。

这时，我们可以使用或运算来判断这些条件是否有满足的情况。

三、非运算非运算是逻辑运算中的另一种基本运算，也称为“非”操作。

非运算的结果是输入变量的反面，即如果输入变量为真（即为1），则非运算结果为假（即为0）；如果输入变量为假（即为0），则非运算结果为真（即为1）。

非运算的运算符通常用符号“¬”或“!”表示。

例如，对于一个输入变量A，¬A表示A的非运算结果。

非运算在实际生活中也有一些应用。

例如，当我们需要判断一个条件是否不成立时，我们可以使用非运算来得出相反的结论。

四、异或运算异或运算是逻辑运算中的另一种基本运算，也称为“异或”操作。

异或运算的结果只有在输入变量不同时为真时才为真，否则为假。

异或运算的运算符通常用符号“⊕”或“xor”表示。

例如，对于两个输入变量A和B，A⊕B表示A和B的异或运算结果。

异或运算在实际生活中也有一些应用。

例如，在某些情况下，我们需要判断两个条件是否恰好有一个满足，即只有一个条件为真，而另一个条件为假。

逻辑运算
一、简介
逻辑运算是数字符号化的逻辑推演法，包括联合、相交、相减。

在图形处理操作中引用了这种逻辑运算方法以使简单的基本图形组合产生新的形体，并由二维逻辑运算发展到三维图形的逻辑运算。

由于布尔在符号逻辑运算中的特殊贡献，很多计算机语言中将逻辑运算称为布尔运算，将其结果称为布尔值。

二、基本概念
逻辑运算：在逻辑运算中，有与、或、非三种基本逻辑运算。

表示逻辑运算的方法有多种，如语句描述、逻辑代数式、真值表、卡诺图等。

三、逻辑运算符
在形式逻辑中，逻辑运算符或逻辑联结词把语句连接成更复杂的复杂语句。

1、逻辑“与”AND：指两个条件同时成立。

如“在家偷玩游戏”与“妈妈回家了”，可以将它们组成“在家偷玩游戏且妈妈回家了”。

2、逻辑“或”OR：指两个条件中的任意一个成立。

如“晚餐吃蛋糕”或“晚餐吃炸鸡”，可以组成“晚餐吃蛋糕或炸鸡，我会很开心”。

3、逻辑“非”NOT：指将原结果做相反的计算。

如条件“飞机飞行”，结果“下飞机”可以组成“飞机不飞行时，才能下飞机”。

四、各种编程语言中的逻辑运算符。

基本的逻辑运算逻辑运算是数学和计算机科学中重要的概念之一。

它是指通过一些特定的规则和操作，将一个或多个输入值映射为一个输出值的过程。

本文将从逻辑运算的基本形式出发，逐步介绍与之相关的概念和应用。

我们需要了解逻辑运算的基本组成部分——逻辑门。

逻辑门是一种由电子元件组成的电路，它能够实现特定的逻辑运算。

最常见的逻辑门有与门、或门、非门和异或门等。

与门的输出只有在所有输入都为真时才为真，或门的输出只要有一个输入为真就为真，非门的输出是输入的反值，异或门的输出只有在输入值不同时才为真。

逻辑运算可以通过组合多个逻辑门来实现更复杂的功能。

例如，通过将多个与门和非门连接起来，可以构建出一个与非门（NAND）电路。

与非门的输出只有在所有输入都为真时才为假，否则为真。

事实上，与非门本身已经足够强大，可以用来实现所有其他的逻辑门，因此被广泛应用于计算机的设计和制造中。

逻辑运算在计算机科学中扮演着重要的角色。

例如，在逻辑电路中，逻辑门的组合可以实现各种计算和控制功能。

在计算机的中央处理器中，逻辑运算用于实现算术运算、逻辑判断和控制流程等操作。

逻辑运算也被广泛应用于数字电路、通信系统和人工智能等领域，为各种应用提供了强大的计算和决策能力。

除了基本的逻辑运算，还有一些常用的逻辑运算符号和表达方式。

例如，逻辑与运算可以用符号“∧”表示，逻辑或运算可以用符号“∨”表示，逻辑非运算可以用符号“¬”表示。

这些符号可以使逻辑表达更加简洁和直观。

逻辑运算在数学推理和证明中也发挥着重要的作用。

通过运用逻辑运算的规则和定律，我们可以从已知条件推导出新的结论。

逻辑运算可以帮助我们识别和排除逻辑错误，提高思维的准确性和严谨性。

在生活中，逻辑运算也有着广泛的应用。

例如，在解决问题和做决策时，我们常常需要进行逻辑思考和逻辑推理。

通过运用逻辑运算的原理和方法，我们可以更好地分析问题、归纳总结和做出正确的判断。

逻辑运算是数学和计算机科学中重要的概念，它通过一些特定的规则和操作将输入映射为输出。

数字电路是一种用来处理数字信号的电路，它由逻辑门组成，可以实现各种逻辑运算。

在数字电路中，最基本的三种逻辑运算分别是与运算、或运算和非运算。

本文将对这三种逻辑运算进行详细介绍，以帮助读者更好地理解数字电路的基本原理和运作方式。

1. 与运算与运算是指在两个信号同时为高电平时，输出为高电平；否则输出为低电平。

在数字电路中，与运算通常由与门来实现。

与门有两个输入端和一个输出端，只有在两个输入端同时为高电平时，输出端才会输出高电平。

与门的逻辑符号通常表示为“∧”。

2. 或运算或运算是指在两个信号中至少有一个为高电平时，输出为高电平；只有在两个输入端同时为低电平时，输出端才会输出低电平。

在数字电路中，或运算通常由或门来实现。

或门同样有两个输入端和一个输出端，只要两个输入端中至少有一个为高电平，输出端就会输出高电平。

或门的逻辑符号通常表示为“∨”。

3. 非运算非运算是指将输入信号取反，即如果输入信号为低电平，则输出为高电平；如果输入信号为高电平，则输出为低电平。

在数字电路中，非运算通常由非门来实现。

非门只有一个输入端和一个输出端，其输出信号与输入信号相反。

非门的逻辑符号通常表示为“¬”。

通过这三种最基本的逻辑运算，数字电路可以实现各种复杂的逻辑功能。

通过组合多个与门、或门和非门，可以构建出加法器、减法器、乘法器、除法器等各种算术逻辑单元，从而实现数字信号的加减乘除运算。

这三种逻辑运算的组合还可以实现逻辑判断、比较、选择等功能，为数字系统的设计和实现提供了基础。

数字电路中的与运算、或运算和非运算是最基本的逻辑运算，它们是数字电路的基石。

通过这三种逻辑运算，我们可以实现各种复杂的数字逻辑功能，从而构建出功能强大的数字系统。

希望本文对读者理解数字电路和逻辑运算有所帮助，谢谢阅读！上文中我们已经介绍了数字电路中最基本的三种逻辑运算，接下来我们将继续探讨这些逻辑运算在数字电路中的应用以及它们的扩展。

4. 异或运算异或运算是指在两个信号不输出为高电平；两个输入端相同时输出为低电平。

三种基本的逻辑运算关系在数学和计算机科学中，逻辑运算关系是基本的逻辑概念，它们帮助我们理解和操控事物之间的关系。

逻辑运算关系主要有三种：与（AND）、或（OR）和非（NOT）。

下面我们将对每一种逻辑运算关系进行详细解释，以帮助读者更好地理解它们的含义和应用。

首先，我们来介绍与运算（AND）。

与运算是指两个条件同时满足时结果为真，否则结果为假。

与运算可以用来判断多个条件是否同时成立。

比如，在一个餐厅中，为了让顾客享受到美味的菜品，我们可以设置一个与运算条件，只有当顾客同时点了主菜和甜点时，才会上菜，否则不会上菜。

这样可以保证顾客们只有在满足两个条件的情况下才能获得他们所期望的美食。

其次，让我们介绍或运算（OR）。

或运算是指两个条件中只要有一个满足时结果为真，只有当两个条件都不满足时结果为假。

或运算可以用来判断多个条件中是否有至少一个成立。

例如，假设你参加了一场晚会，门口有一个守卫，他会检查你是否持有邀请函或者是否是VIP。

只要你满足其中一种条件，就可以进入晚会，否则你将无法进入。

这就是或运算的用途。

最后，让我们介绍非运算（NOT）。

非运算是指对某个条件取反，如果原来的条件为真，则取反后为假；如果原来的条件为假，则取反后为真。

非运算可以用来转换一个条件的逻辑状态。

例如，如果你希望你的自行车不被小偷盗走，你可以在停车处贴上一个标志，上面写着“此车容易损坏”。

这个标志的作用是利用非运算，通过传递一个虚假的信息，让小偷们误以为你的自行车不值得被盗窃，从而不会选择你的车作为目标。

综上所述，与、或和非是三种基本的逻辑运算关系。

它们在我们日常生活中无处不在，用来判断和操纵不同条件之间的关系。

通过了解和灵活运用这些逻辑运算关系，我们可以更加理性地思考和决策，提高我们的生活品质和工作效率。

最基本的逻辑运算基本的逻辑运算有与、或和非三种。

与运算是指两个命题都为真时，结果为真；否则，结果为假。

例如，如果今天既是周末又是晴天，那么我就去户外运动。

只有当两个条件都满足时，我才会去户外运动，否则我将选择其他活动。

或运算是指两个命题中至少一个为真时，结果为真；只有当两个条件都为假时，结果才为假。

例如，如果今天是周末或者是晴天，那么我就去户外运动。

只要有一个条件满足，我就会去户外运动，不论另一个条件是否满足。

非运算是指对一个命题取反。

例如，如果今天不下雨，那么我就去户外运动。

只要不下雨，我就会去户外运动，否则我将选择其他活动。

除了与、或和非运算，还有其他衍生的逻辑运算，如异或、蕴含和等价等。

异或运算是指两个命题中有且只有一个为真时，结果为真；否则，结果为假。

例如，如果今天是周末或者是晴天，但不能同时满足这两个条件，那么我就去户外运动。

只有一个条件满足时，我才会去户外运动，否则我选择其他活动。

蕴含运算是指当前提为真时，结论为真；否则，结果为假。

例如，如果今天是周末，那么我就去户外运动。

只有当条件满足时，我才会去户外运动，否则我选择其他活动。

等价运算是指两个命题具有相同的真值。

例如，如果今天是周末或者不下雨，那么我就去户外运动。

只要满足其中一个条件，我就会去户外运动，因为这两个条件具有相同的结果。

逻辑运算在日常生活中有着广泛的应用。

它们帮助我们进行推理和判断，使我们能够做出明智的决策。

通过对不同条件的组合和运算，我们可以得出不同的结论，从而更好地理解和解决问题。

除了基本的逻辑运算，还有其他复杂的逻辑问题需要我们思考和解决。

例如，概率逻辑运算可以用来描述随机事件的概率；模态逻辑运算可以用来描述可能性和必然性。

这些逻辑运算在数学、计算机科学、哲学等领域都有重要的应用。

逻辑运算是我们思考和推理的基础，它们帮助我们理解和解决问题。

通过灵活运用不同的逻辑运算，我们可以得出准确和有效的结论，提高我们的决策能力和思维逻辑。

逻辑运算逻辑代数的基本运算比较简单，只有三种：“与”运算、“或”运算和“非”运算。

任何复杂的逻辑运算都可由这三种基本逻辑运算构成。

如，广泛采用的“与非”、“或非”、“与或非”、“异或” 。

、“同或”等逻辑运算，它们的逻辑关系可以由以上三种基本运算导出。

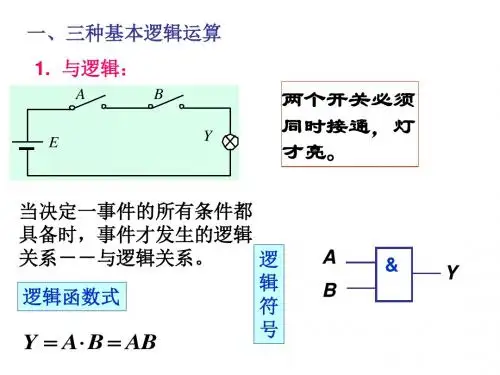
1．“与”运算当决定一事件的所有条件都具备之后，这事件才会发生，称这种因果关系为“与”逻辑关系，或称为“与”逻辑运算或逻辑乘。

条件用逻辑变量“A，B…..”表示，变量取值为1，表示条件具备;取值为0,表示条件不具备。

事件用F表示，只有发生（用1表示）和不发生（用0表示）两种取值。

“与”逻辑运算用表达式表示为：F=A·B 或者F=A ∧B一般简写为：F=AB，把此式称为变量A、B相“与”的逻辑表达式。

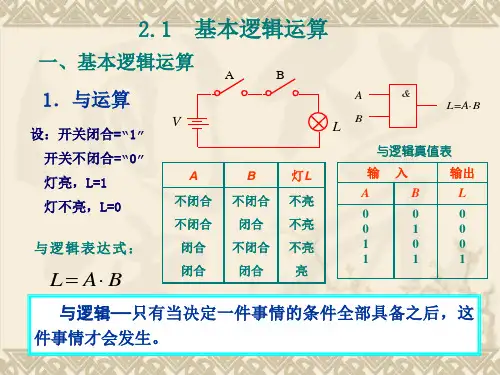
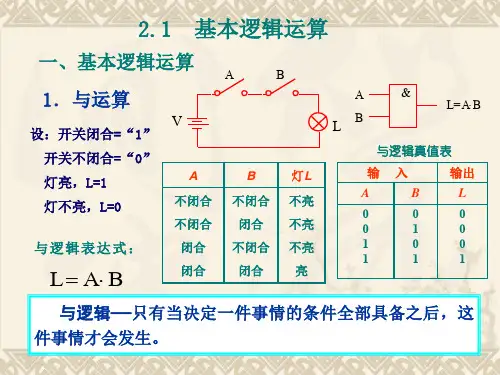
用两个串联的开关A、B控制一盏灯，如图1(a)所示。

灯亮的条件是开关A“与”开关B同时处在合上位置。

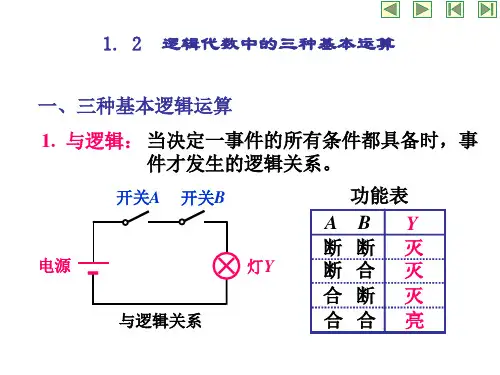
假定灯亮为“1”，不亮为“0”，开关在合上位置为“1”，在断开位置为“0”，那么，把灯的状态和两个开关所处位置之间的关系列表，如图1(b)所示。

把这种表称为真值表(或称为功能表)。

常用真值表来表示逻辑命题的真假关系。

把所有的条件(输入变量)的全部组合以表格形式列出来，这里为A、B，再把在每一种组合下对应的事件(函数)的值F求出，这张表格就是真值表。

因为每个条件有两种状态“0”、“1”，因此，n个条件就有2n个组合。

图1(b)为A“与”B 的真值表。

同一逻辑函数只可能有唯一的真值表！2．“或”运算当决定事件发生的各种条件中，只要有一个或一个以上条件具备时，这事件就会发生，这样的因果关系称为“或”逻辑关系，或称逻辑加。

“或”运算的逻辑表达式为：F=A+B 或者F=A∨B 。

用并联的两个开关A、B控制一盏灯，如图2(a)所示，只要开关A“或”开关B在合上位置，灯就亮。

按照前面假定来赋值“0”、“1”，列出真值表，如图2(b)所示。

3．“非”运算“非”运算，就是否定，或者称为求反。