决策方法计算题

1．某企业生产甲产品，单位销售价格为15元／件，单位变动成本是5元／件，年固定成本为180000元。

问：该企业的盈亏平衡点产量是多少？2．某公司计划未来5年生产某种产品，需要确定产品批量。

根据预测估计，这种产品的市场状况的概率是：畅销为0.2，一般为0.5，滞销为0.3。

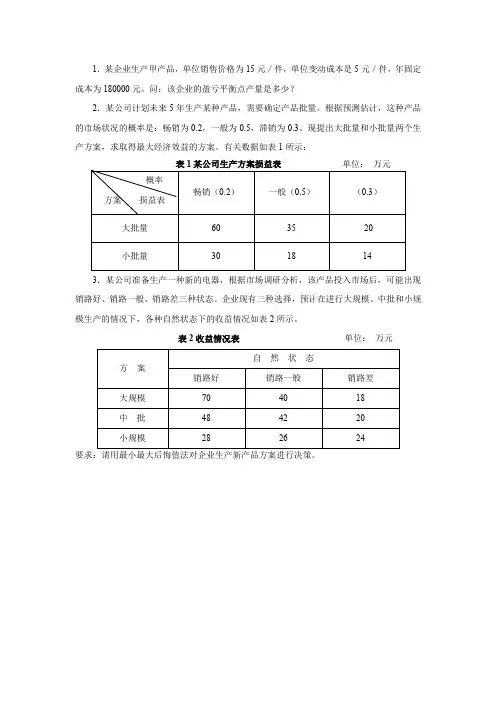
现提出大批量和小批量两个生产方案，求取得最大经济效益的方案。

有关数据如表1所示：3．某公司准备生产一种新的电器，根据市场调研分析，该产品投入市场后，可能出现销路好、销路一般、销路差三种状态。

企业现有三种选择，预计在进行大规模、中批和小规模生产的情况下，各种自然状态下的收益情况如表2所示。

表2收益情况表单位：万元要求：请用最小最大后悔值法对企业生产新产品方案进行决策。

4.某企业准备生产一种新产品，根据市场调研分析，该产品投入市场后，可能出现销路好、销路一般、销路差三种状态，其发生的概率分别为0.3、0.5、0.2。

企业现在有三种选择，预计进行大批、中批和小批生产，方案使用期限均为5年。

各方案在各种自然状态下的收益如下表所示。

单位：万元要求：请用决策树法对企业生产新产品方案进行决策5. 某企业准备生产某种产品，但对市场销量不能确定，经估算各自然状态下的损益值如下表所示，三种方案如下：方案一：改建原有罐头生产线，投资不多，风险不大，损益值一般；方案二：新建一条生产线，投资大，可能收益高，风险大；方案三：和某大厂搞联合，利润分成投资少，收益少，风险小。

某企业准备生产产品的三种备选方案的损益值单位：万元分别运用大中取大法、小中取大损益值法，最小最大后悔值法选出最优方案。

6. 某企业准备生产一种新产品，对未来三年市场预测资料如下；现有三个方案可供选择，即新建一车间，需要投资140万元；扩建原有车间，需要投资60万元，协作生产需要投资40万元。

三个方案在不同自然状态下的年收益见表。

单位：万元要求：（1）绘制决策树；（2）方案选优。

7.某企业计划未来5年生产一种新产品，根据市场调研分析，该产品投入市场后，可能出现销路好、销路一般、销路差三种状态，其发生的概率分别为0.2、0.5、0.3。

完整版决策与决策方法习题及答案决策是指在不同情况下，通过分析和权衡各种因素来做出判断和选择的过程。

在现代社会中，决策已经成为了各个领域的核心要素之一。

无论是在管理、经济、政治还是日常生活中，决策都扮演着至关重要的角色。

为了培养人们的决策能力，许多关于决策和决策方法的习题被广泛提供。

以下是一些典型的决策与决策方法习题及答案，帮助读者更好地理解决策过程。

题目一：某公司决定推出一款新产品。

该产品的市场细分为A、B、C三个部分，每个部分的预期销售额、预期成本和预期利润如下表所示：市场细分 | 预期销售额（万元） | 预期成本（万元） | 预期利润（万元）A市场 | 60 | 40 | 20B市场 | 80 | 65 | 15C市场 | 40 | 30 | 10应该选择哪个市场细分以最大化整体利润？答案：为了确定最佳决策，我们可以计算每个市场细分的预期利润率（预期利润除以预期销售额）。

通过比较这些利润率，我们可以选择具有最高利润率的市场细分。

A市场的预期利润率为 20/60 = 0.33B市场的预期利润率为 15/80 = 0.19C市场的预期利润率为 10/40 = 0.25由此可见，A市场具有最高的预期利润率，因此选择A市场会最大化整体利润。

题目二：某公司需要决定是否投资于一个新项目。

该项目的投资额为100万元，预期利润为30万元。

公司使用折现率10%来评估项目的价值。

项目的净现值是多少？答案：净现值是指项目的预期现金流入与现金流出之间的差额。

为了计算净现值，我们需要将预期利润按照折现率进行折现，并减去投资额。

净现值 = 预期利润 / (1 + 折现率) - 投资额= 30 / (1 + 0.1) - 100= 30 / 1.1 - 100= 27.27 - 100= -72.73由于净现值为负数，这表示该项目的回报率低于折现率，因此不值得投资。

题目三：某家电店想要提高电视机的销量。

他们分析了市场数据，得出以下结论：在市场上，价格和销量呈反比关系。

某企业生产A产品，预计单位产品的价格为6000元，固定成本总额为630 万元，单位产品变动成本为3000元。

求：1. 盈亏平衡点2. 企业为了获利510 万元，应达到的产量和销售收入为多少？3. 若设计能力为4000 台，那么，达到设计能力时，获利期望值为多少？解：(1) 盈亏平衡点Q=C/(P-V)=630 X 107(6000-3000)=2100(台)S 0=2100x 6000=1260(万元)(2) 若企业为获利510 万元，应达到的销售量为：Q *=(C+B)/(P-V)=(510+630) X 104/(6000-3000)=3800( 台)S *=3800X 6000=2280(万元)(3) 若设计能力为4000 台，那么，达到设计能力时，获利期望值是：B=(P-V)X-C=(6000 －3000)X 4000－630X 104=570(万元)某肉食加工厂去年6—8月份熟食日销量统计资料如表所示。

每箱利润为50元，如果当天销售不出去，每剩一箱就要支付30元冷藏保管费，预计今年6—8月份需求量与去年同期无变化。

决策问题是日产计划定为多少，能使工厂获利最大？解;收益矩阵如下:期望利润的计算如下:(4,400 X 0.2) +(5,200 X 0.4)+(6,000 X 0.3)+(6,000 X 0.1)=5,360(元)从计算结果看，日产120箱时，期望利润为5,360元，大于其它方案，应按日产120箱方案决策。

备注：由于各个方案的期望利润，都是将该方案在各种自然状态下的收益值与损失值按统计概率进行加权计算，它掩盖了偶然情况下的损失，所以，选择哪一个方案都有一定的风险。

某企业为增加某产品的产量而设计了三个可行方案：一是投资100万元新建生产车间；二是投资50万元，扩建老车间；三是转包给其他厂生产，设使用期为5年，自然状态如表：解:据题意画决策树42-8308184决策树的结构图E1=(70 X 0.6 - 20 X 0.4) X 5- 100=70(万元) E2=(50 X 0.6+20 X 0.4) X 5-50=140(万元)E3=(30 X 0.6+10 X 0.4) X 5=110(万元)••• E2>E3>E1•••选取扩建方案。

管理决策博弈法计算题（最新版）目录1.管理决策博弈法简介2.管理决策博弈法计算题的类型3.管理决策博弈法计算题的解法4.管理决策博弈法计算题的应用实例5.总结正文【1.管理决策博弈法简介】管理决策博弈法是一种用于解决管理决策问题的数学方法，它基于博弈论，通过分析决策者之间的相互作用，研究决策者的策略选择和决策结果。

管理决策博弈法可以帮助决策者在复杂的决策环境中找到最佳的决策策略，从而实现组织目标。

【2.管理决策博弈法计算题的类型】管理决策博弈法计算题主要包括以下几种类型：（1）静态博弈计算题：静态博弈是指在一次性决策中，决策者需要同时做出决策，并且每个决策者的决策不会受到其他决策者的影响。

（2）动态博弈计算题：动态博弈是指在多次性决策中，决策者需要根据其他决策者的决策结果，调整自己的决策策略。

（3）完全信息博弈计算题：完全信息博弈是指决策者拥有完全的信息，可以准确地预测其他决策者的决策结果。

（4）不完全信息博弈计算题：不完全信息博弈是指决策者拥有不完全的信息，无法准确地预测其他决策者的决策结果。

【3.管理决策博弈法计算题的解法】管理决策博弈法计算题的解法主要包括以下几种：（1）纳什讨价还价解法：纳什讨价还价解法是一种用于解决静态博弈问题的方法，它假设每个决策者都会选择最优的策略，并且每个策略都会考虑到其他决策者的可能策略。

（2）重复博弈解法：重复博弈解法是一种用于解决动态博弈问题的方法，它假设决策者会在多次决策中，根据其他决策者的决策结果，调整自己的策略。

（3）贝叶斯博弈解法：贝叶斯博弈解法是一种用于解决不完全信息博弈问题的方法，它假设决策者会根据自己拥有的信息，对其他决策者的策略进行概率分析，并选择最优的策略。

【4.管理决策博弈法计算题的应用实例】管理决策博弈法计算题在实际应用中，可以解决许多管理决策问题，例如：（1）定价决策：在市场竞争中，企业需要根据竞争对手的价格策略，选择最佳的定价策略。

最佳现⾦持有量决策⽅法和例题最佳现⾦持有量Ⅰ、考点分析：最佳现⾦持有量的确定⽅法有成本分析模式、存货模式、随机模式和现⾦周转模式。

1、成本分析模式：（1）含义：成本分析模式是通过分析持有现⾦的成本，寻找使持有成本最低的现⾦持有量。

（2）现⾦持有成本：机会成本、管理成本、短缺成本（3）决策原则：现⾦持有总成本最低时的现⾦持有量即机会成本、管理成本和短缺成本之和最低时的现⾦持有量。

【提⽰】成本分析模式是⼀种传统的分析⽅法，其中机会成本、管理成本和短缺成本三项之和的总成本线是⼀条抛物线，该抛物线的最低点即为持有现⾦的最低总成本。

2、存货模式：（1）含义：存货模式是通过分析机会成本与交易成本，寻找使这两者总成本最低的现⾦持有量。

（2）考虑相关成本：机会成本、交易成本。

（3）计算公式：式中：C*――最佳现⾦持有量T――⼀定时期内的现⾦需求量F――每次现⾦转换的交易成本K――持有现⾦的机会成本率【提⽰】①现⾦交易成本假定每次的交易成本是固定的，且企业⼀定时期内现⾦使⽤量是确定的；②存货模式模式简单、直观；主要是假定现⾦的流出量稳定不变，实际上这是很少的。

3、随机模式（1）基本原理：A：测算出现⾦持有量的上限和下限；B：当持有现⾦量达到控制上限时，购⼊有价证券，使现⾦持有量下降；C：当持有现⾦量降到控制下限时，则出售有价证券，换回现⾦，使现⾦持有量回升；D：若持有现⾦量在控制上下限之内的，是合理的，不必理会。

（2）应⽤前提：企业的现⾦未来需求总量和收⽀不可预测，此法计算出来的现⾦持有量⽐较保守。

现⾦存量的上限（H）的计算公式：H＝3R－2L式中：b――每次有价证券的固定转换成本i――有价证券的⽇利息率δ――预期每⽇现⾦余额变化的标准差（可根据历史资料测算）L――现⾦存量的下限4、现⾦周转模式：（1）确定现⾦周转期现⾦周转期=应收账款周转期+存货周转期-应付账款周转期（2）确定现⾦周转率确定现⾦周转率=计算期天数/现⾦周转期（3）确定最佳现⾦持有量确定最佳现⾦持有量=全年现⾦需求量/现⾦周转率【提⽰】计算简单明了，易于计算，但有⼀定的前提条件。

计算题 一 1.为生产甲产品，小行星公司设计了两个基本方案：一是建大工厂，二是建小工厂。

如果销路好，3年以后考虑扩建。

建大工厂需投资300万元，建小工厂需投资160万元，3年后扩建另需投资140万元。

扩建后可使用7年，其年度损益值与大工厂相同。

每种自然状态的预测概率及年度损益值如下表： 前 3 年 后7 年 根据上述资料试用决策树法做出决策。

 四、计算题（15分） 答：建大厂收益=581-300=281 建小厂收益=447-160=287 所以应选择建小厂方案。

 二 山姆公司的生产设备已经落后，需要马上更新。

公司有人认为，目前产品销路增长，应在更新设备的同时扩大再生产的规模。

但也有人认为，市场形势尚难判断，不如先更新设备，3年后再根据形势变化考虑扩大再生产的规模问题。

这样，该公司就面临着两个决策方案。

决策分析的有关资料如下： A、现在更新设备，需投资35万元，3年后扩大生产规模，另需投资40万元。

 B、现在更新设备的同时扩大再生产的规模，需投资60万元。

 C、现在只更新设备，在销售情况良好时，每年可获利6万元；在销售情况不好时，每年可获利4、5万元。

 D、如果现在更新与扩产同时进行，若销售情况好，前3年每年可获利12万元；后7年每年可获利15万元；若销售情况不好，每年只获利3万元。

 E、每种自然状态的预测概率如下表 前 3 年 后7 年 答案：根据上述资料试用决策树法做出决策。

 结点7收益值=0、85×7 × 15+0、15 ×7 ×3=92、4（万元） 结点8收益值=0、85×7 ×6+0、15 ×7 ×4、5=40、4（万元） 结点9收益值=0、1×7 × 15+0、9 ×7 ×3=29、4（万元） 结点10收益值=0、1×7 × 6+0、9 ×7 ×4、5=32、6（万元） 结点1收益值=0、7×[52、4+（3 × 6）]+0、3 ×[32、6+（3 × 4、5）] =63、1（万元） 结点2收益值=0、7×[92、4+（3 × 12）]+0、3 ×[29、4+（3 × 3）] =101、4（万元） 答：用决策树法进行决策应选择更新扩产方案，可获得收益41、4万元。