光程与光程差 半波损失

再论光波的半波损失作者：曹冬梅来源：《科学与财富》2011年第12期[摘要] 半波损失是大学物理中的重点和难点问题。

本文根据半波损失定义明确了其产生条件，重申了半波损失和附加光程差的区别与联系，最后结合薄膜干涉实例对附加光程差表达式作了针对性的分析。

[关键词] 半波损失薄膜干涉附加光程差引言半波损失问题是很久以来人们一直关注的问题，大量的文献从不同的角度对半波损失问题进行了探讨［1-3］。

由姚启钧原著的光学教材在提到半波损失对等倾干涉和等厚干涉反射光光程差的影响时，认为只要薄膜处于同一介质中，必然有额外光程差，我们在此取负号。

然而在等厚干涉一节的例1.2中却把附加光程差一项取为正号［4］。

在前一部分教材中“规定”附加光程差项取负号，而在例题运算中却取正号，附加光程差一项取正号和负号时有区别吗? 附加光程差与半波损失之间又有怎样的联系？1.半波损失半波损失，就是光在正入射或掠入射的情况下，从光疏（折射率相对小的）介质射向光密（折射率相对大的）介质被反射时，产生相位π的突变，相当于损失半个波长的光程，称为半波损失［5］。

当光从光疏介质射向光密介质，在垂直入射和掠入射时反射光有半波损失现象，我们可以由电磁场理论中的菲涅耳公式予以解释［4］。

当n1＜n2时，无论一束光是垂直入射还是掠入射，在介质界面附近反射光矢量的振动方向都与入射光矢量的振动方向相反，都将出现光矢量在同一点相位突变的情形，即有半波损失发生。

那么对于斜入射，反射光矢量的垂直分量与入射光矢量的垂直分量的振动方向始终相反，但是，平行分量的方向之间却成一定的角度，此时比较它们的相位是没有绝对意义的。

故一般描述为“光从光疏介质入射到光密介质反射时具有半波损失”，这样很容易理解为：不管入射角为多少，只要光从光疏介质入射到光密介质,反射光矢量与入射光矢量就有相位突变π,相当于反射时产生了半波损失，似乎半波损失产生条件与入射角无关。

事实上半波损失的产生，不仅取决于界面两侧介质的折射率，还取决于入射角的大小［6］。

目录半波损失定义半波损失理论的应用半波损失的原因定义光从光疏介质射向光密介质时反射过程中，如果反射光在离开反射点时的振动方向相对于入射光到达入射点时的振动方向恰好相反，这种现象叫做半波损失。

从波动理论知道，波的振动方向相反相当于波多走（或少走）了半个波长的光程。

入射光在光疏媒质中前进，遇到光密媒质界面时，在掠射或垂直入射2种情况下，在反射过程中产生半波损失，这只是对光的电场强度矢量的振动而言。

如果入射光在光密媒质中前进，遇到光疏媒质的界面时，不产生半波损失。

不论是掠射或垂直入射，折射光的振动方向相对于入射光的振动方向，永远不发生半波损失。

光的干涉现象是有关光的现象中的很重要的一部分，而只要涉及到光的干涉现象，半波损失就是一个不得不考虑的问题。

光在不同介质表面反射时，在入射点处，反射光相对于入射光来说，可能存在半波损失，半波损失可以通过直观的实验现象——干涉花样——来得到验证。

半波损失理论的应用半波损失理论在实践生活中有很重要的应用，如：检查光学元件的表面，光学元件的表面镀膜、测量长度的微小变化以及在工程技术方面有广泛的应用。

半波损失的原因在洛埃镜实验中，如果将屏幕挪进与洛埃镜相接触。

接触处两束相干波的波程差为零，但实验发现接触处不是明条纹，而是暗条纹。

这一事实说明洛埃镜实验中，光线自空气射向平面镜并在平面镜上反射后有了量值为∏的位相突变，这也相当于光程差突变了半个波长。

光在反射时为什么会产生半波损失呢？这是和光的电磁本性有关的，可通过菲涅耳公式来解释。

在任何时刻，我们都可以把入射波、反射波和折射波的电矢量分成两个分量，一个平行入射面，另一个垂直入射面。

有关各量的平行分量和垂直分量依次用指标p和s表示。

以i1、i1´ 和i2分别表示入射角、反射角和折射角，它们确定了各波的传播方向。

以A1、A1´、A2来依次表示入射波、反射波和折射波的电矢量的振幅，它们的分量相应就是Ap1、Ap1´、Ap2和As1、As1´、As2。

光从波疏媒质到波密媒质表面上反射时产生半波损失的原因2008-07-02 16:33光从波疏媒质到波密媒质表面上反射时产生半波损失的原因何万勇（楚雄师范学院物理与电子科学系云南 675000）摘要：本文介绍什么是半波损失，并用电磁场理论中的菲涅耳公式予以解释。

最后得出光从波疏媒质到波密媒质表面上反射时产生半波损失的原因是，反射光相对于入射光产生了π的相位突变。

关键词：半波损失菲涅耳公式光波波疏媒介波密媒介相位中图分类号： 043 文献标识码：文章编号：引言：当光从波疏媒质到波密媒质表面上反射时将会产生波损失，那到底什么是半波损失呢？所谓“半波损失"，就是当光从折射率小的光疏介质射向折射率大的光密介质时，在入射点，反射光相对于入射光有相位突变π，即在入射点反射光与入射光的相位差为π，由于相位差π与光程差λ\２相对应，它相当于反射光多走了半个波长λ\２的光程，故这种相位突变π的现象叫做半波损失。

半波损失仅存在于当光从光疏介质射向光密介质时的反射光中，折射光没有半波损失。

当光从光密介质射向光疏介质时，反射光也没有半波损失。

“半波损失”现象可以由电磁场理论中的菲涅耳公式予以解释。

光波是频率范围很窄（400nm～700nm）的电磁波。

在光波的电矢量E→和磁矢量H→中，能够引起人眼视觉作用和光学仪器感光作用的主要是电矢量E→，所以把光波中的电矢量E→叫做光矢量。

电磁波（光波）通过不同介质的分界面时会发生反射和折射。

根据麦克斯韦的电磁场理论，在分界面处，入射波、反射波、折射波的振幅矢量E→１、E`→１、E→２沿垂直于入射面的分量和沿平行于入射面的分量之间的关系满足菲涅耳公式：由文献[1]可知，菲涅耳公式为公式(1)~公式(4)：E`s1/Es1=-sin(i-r)/sin(i+r) (1)E`p1/Ep1=tg(i-r)/tg(i+r) (2)Es2/Es1=2sin(r)cos(i)/sin(i+r) (3)Ep2/Ep1=2sin(r)cos(i)/[sin(i+r)cos(i-r)] (4)设Es1与Ep1的合矢量为E1；E`s1与E`p1的合矢量为E`1。

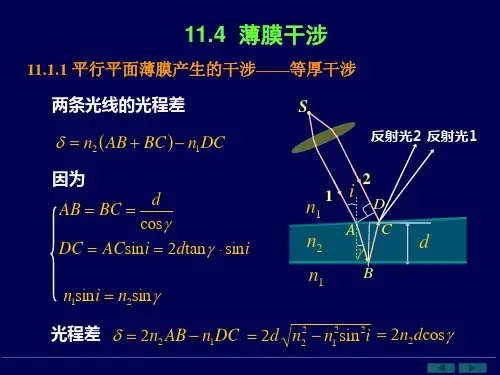
第3节光程和光程差双缝干涉21ϕϕ=，212()r r πϕλ∆=--νλ/c =：光在真空中的波长1r ，2r ：几何路程双缝和屏之间充满某种均匀透明介质n 介质中的光速n c V /=介质中光的波长n n cV //λννλ==='=∆ϕ)(212r r -'-λπ1r 2r 3r==-'-)(212r r n n λπ)(212nr nr --λπ， 1n 2n 3n定义：光程nr =∆∑=++=∆i i r n r n r n 2211，真空中：r =∆光程差12∆-∆=δ位相差=∆ϕδλπ2-在相同时间内，若光在介质中走过的几何路程为r 则光在真空中走过的几何路程为nr 光在介质中走过r 的路程产生的位相变化=光在真空中走过nr 的路程产生的位相变化光程：光在介质中走过的路程折合成光在真空中走过的路程 例：双缝干涉 P在光路2上放一厚度 S 为t 折射率为n 的玻璃片 t n r r r nt t r )1(1212-+-=-+-=δ 2S =∆ϕδλπ2-=])1([212t n r r -+--λπλ：光在真空中的波长透镜的光程F ' F透镜只改变光的传播方向，而不引起附加光程差第4节薄膜干涉（1）等厚干涉（2）等倾干涉一、 等厚干涉的一般理论1、 光路图 厚度不均匀薄膜2n i ：入射角 薄膜上下表面产生的两条反射光 在薄膜上表面相遇相干迭加 32、 光程差 DC n BC AB n 12)(-+=δ，i n n e 22122sin 2-=δ 312,n n n >，光线2有半波损失，光线1没有，应加上2/λ 312,n n n <，光线2没有半波损失，光线1有，应加上2/λ 321n n n <<，光线2和光线1都有半波损失， 不加2/λ 321n n n >>，光线2和光线1都没有半波损失，不加2/λ 3、 等厚干涉条纹 ⎪⎩⎪⎨⎧∈+∈>=<+-=干涉相消）（干涉加强N k k N k k i n n e 2122sin 222122λλλδk ：干涉级，k 的取值必须保证0≥e干涉条纹形状与薄膜等厚线形状相同说明：（1）用日光照射薄膜，呈现彩色条纹（2）从薄膜上方看到的是反射光的干涉 从薄膜下方看到的是透射光的干涉 透射光光程差-='sin 222122δi n n e 反射光干涉加强时，透射光干涉相消反射光干涉相消时，透射光干涉加强例：用日光垂直照射空气中m e μ40.0=、折射率为50.1的玻璃片 求：可见光范围，哪些波长的光反射加强、哪些波长的光透射加强？解：反射加强条件222sin 2222122λλδ+=+-=e n i n n e =λkλ=1242-k e n 3=k ，m μλ48.01321040.050.146=-⨯⨯⨯⨯=- 透射加强条件（反射光相消条件）e n i n n e 2221222sin 2=-=δ=λk ，λ=ke n 22 2=k ，m μλ60.0=；3=k ，m μλ40.0=二、 几种重要的薄膜干涉1、 劈尖干涉用波长λ的单色光垂直照射劈尖 0=i><+-=2sin 222122λδi n n e 空气劈尖22λδ+=e （空气中的玻璃劈尖22λδ+=ne ⎪⎩⎪⎨⎧=+==+=暗纹明纹,2,1,02)12(,3,2,122k k k k e λλλδ 玻璃劈尖明纹中心下面空气薄膜厚度λ412-=k e ，λ41，λ43，λ45，暗纹中心下面空气薄膜厚度λk e 21=， 0，λ1，λ，等厚线是平行棱边的直线 条纹是平行棱边的直条纹相邻两明纹或两暗纹下面空气薄膜厚度差2/λ=∆e 相邻两明纹或两暗纹的 距离θλθsin 2sin /=∆=e l 0 λ4λ2λ4λ λ4θ：劈尖的夹角，条纹均匀分布↓θ，↑l 条纹容易分辨，↑θ，↓l用途：已知λ，测量l ，求θ；已知θ，测量l ，求λ； 检验玻璃表面是否平整棱边处是一暗纹，222λλδ=+=e ，是半波损失的有力证据空气中的玻璃劈尖：n e 2λ=∆，θλsin 2n l =例：mm L 880.28=，用波长m μλ5893.0=的光垂直照射劈尖，测得第一条 明纹到第31条明纹的 距离为mm 295.4 L求：金属丝的直径D解：相邻两明纹的距离 mm l 14317.0131295.4=-=θλsin 2=l ，l 2sin λθ=l L L Ltg D 2sin λθθ=≈≈=mm 05944.0圆柱向右移动，条纹如何变化？L 变窄变密，向右移动 ↓L ，条纹如何变化？ 变窄变密)(22s i n 2/c o s /12d d tg L L N -===λθλθλθ 下面几种情况条纹如何变化？例：用波长λ的单色平行光垂直照射由平板玻璃和工件形成的空气劈尖，观察干涉条纹弯曲，弯曲部分的顶部恰与左边条纹直线部分相切，说明工件上有一凹槽，深度2/λ解；条纹是空气薄膜的等厚线 某条纹弯曲部分的顶部下面空气薄膜厚度与同一条纹上直线部分下面空气薄膜厚度相同工件上必有一凹槽，深度等于相邻两明纹直线 部分对应的空气薄膜厚度差2/λ2、 增透膜与增反膜反射光的光程差 空气1n ><+=222λδe n 薄膜2n 如果反射光干涉加强，增反膜 如果反射光干涉相消，增透膜例：设11=n ，38.12=n ，55.13=n ，用nm 550=λ的黄绿光垂直 照射薄膜，若使反射光强最小求：薄膜最小厚度解：e n 22=δe n 22=δ=2)12(λ+k λ2412n k e +=，0=k ，nm n e 10038.1455042min =⨯==λ 注：1n 、2n 、3n 、e 给定，薄膜只对特定波长的光增透或增反 若用日光照射，反射光中缺少黄绿光，反射光呈蓝紫色 μm。

薄膜干涉光程差公式高中
（原创版）
目录
1.薄膜干涉光程差公式的背景和基本概念
2.薄膜干涉光程差公式的推导和理解
3.薄膜干涉光程差公式在实际应用中的意义和价值
正文
薄膜干涉光程差公式是光学薄膜干涉现象中一个重要的公式。

在光学薄膜干涉中，由于光的波动性和叠加原理，当光线经过一个薄膜时，会在薄膜的前后表面分别反射出一束光线，这两束光线在薄膜内部相遇，形成干涉条纹。

薄膜干涉光程差公式可以用来描述这个现象中的光程差。

这个公式包含三个因素：路程差、介质和半波损。

其中，路程差就是薄膜厚度的两倍，即 2e，再乘以折射率，就是 2ne。

半波损则是由于光的波长和薄膜的厚度不相等，导致光的相位发生改变，从而引起的光程差。

在推导薄膜干涉光程差公式时，需要考虑到两束光线在薄膜内部的传播路径不同，一束光线经过的路程是薄膜的厚度，另一束光线经过的路程是薄膜的厚度加上薄膜的半波长。

因此，两束光线之间的光程差就是薄膜的厚度加上薄膜的半波长。

薄膜干涉光程差公式在实际应用中具有重要的意义和价值。

它可以用来解释和预测薄膜干涉现象中的干涉条纹，这对于光学表面的检验、微小的角度或线度的精密测量、减反射膜和干涉滤光片的制备等都具有重要的作用。

此外，薄膜干涉光程差公式还可以用来分析半波损失引起的附加光程差。

半波损失是由于光的波长和薄膜的厚度不相等，导致光的相位发生改变，从而引起的光程差。

在实际应用中，半波损失往往会对薄膜干涉现象
产生影响，因此，对半波损失的研究和理解也十分重要。

1、光程与光程差：<![endif]>⑴光程：前面讨论双缝干涉时，光始终在同一种介质中传播，两相干光束在叠加点处的相位差决定于它们的波程差。

当讨论光在几种不同的介质中传播时，因光的波长与介质的折射率有关，所以同一束光在不同介质中传播相同距离时，所引起的相位变化是不同的。

可见，在不同介质中传播的两光束间的相位差与传播距离和介质折射率都有关。

设某单色光的频率为ν，在真空中的波长为λ，真空中光速为c，则有，设它在真空中传播距离d，则其相位的变化为该光束在折射率为n的介质中传播的速度为，波长为。

当它在此介质中传播距离d时，其相位的变化为可见，光在折射率为n的介质中传播距离d，相当于在真空中传播距离nd。

见下图：定义：光程定义光程的目的是将光在不同介质中实际传播的距离折算成它在真空中传播的距离。

当一束光经过若干不同介质时：光程L = S ( ni di )⑵光程差与相位差：设S1和S2为频率均为ν的相干光源，它们的初相位相同，分别在折射率为n1和n2的介质中经路程r1和r2到达空间某点P。

n2S1S2pr1r2则这两束光的光程差为相应的相位差为可见，引入光程的概念后，相位差和光程差之间的关系为⑶透镜不引起附加光程差：从物点S发出的不同光线，经不同路径通过薄透镜后会聚成为一个明亮的实像S'，说明从物点到像点，各光线具有相等的光程。

左图：平行于透镜主光轴的平行光会聚在焦点F，从波面A上各点到焦点F的光线A1F，A2F，A3F是等光程的。

中图：平行于透镜副光轴的平行光会聚于焦面F上，从波面B上各点到F'的光线B1F'，B2F'，B3F'是等光程的。

右图：点光源S发出球面波经透镜后成为会聚于像点S'的球面波，S的波面C上的各点到像点S'的光线C1S'，C2S'，C3S'是等光程的。

2、薄膜干涉的光程差公式：设一束单色光a经折射率为n，厚度为d的薄膜上、下表面的反射形成两束平行反射光a'、b'。

发生两次半波损失光程差以下是一篇关于半波损失光程差的文章，详细解释了该现象的原因以及可能的解决方法。

引言：半波损失光程差（Half-Wave Plate Displacement）是光学中一个重要的概念，它会对光线的传播产生影响。

在实际应用中，我们可能会遇到发生两次半波损失光程差的情况。

本文将一步一步解释这一现象的原因，以及可能采取的解决方法。

第一部分：半波损失光程差的定义和特点（300字）半波损失光程差是指由于光线在通过半波片时发生位移而引起的相位变化。

半波片是一种常见的光学元件，它可以改变光线的偏振状态。

当光线从一种振动方向偏振转变为另一种方向时，会产生相位差，从而产生光程差。

在理想情况下，一次半波损失光程差是可控制的，但在实际应用中，我们可能会遇到发生两次半波损失光程差的情况。

第二部分：发生两次半波损失光程差的原因（400字）发生两次半波损失光程差的原因主要有两个。

首先，可能是在光路中存在长度的变化。

当光线通过半波片时，由于光路长度的变化，光线在传播过程中会发生位移，从而导致光程差的变化。

其次，可能是由于材料的厚度变化造成的。

材料的厚度变化会导致光线通过时的相位差发生变化，进而引起光程差的变化。

第三部分：影响和解决方法（500字）发生两次半波损失光程差会对光学系统的性能产生影响。

首先，它会导致光学元件的精度要求提高。

为了尽可能地减小光程差，我们需要更加精确地控制光路的长度和材料的厚度。

其次，它会对光学系统的工作稳定性产生不利影响。

由于光程差的变化，光学系统的性能可能会因此产生波动。

这对于某些特定的应用来说是不可接受的。

为了解决发生两次半波损失光程差的问题，我们可以采取以下方法。

首先，我们需要通过精确的测量和控制光路的长度来减小光程差的变化。

可以使用精密的测量仪器来测量光路的长度，并根据测量结果进行调整。

其次，我们可以使用材料厚度均匀的半波片来减小光程差的变化。

通过选择质量稳定、相对均匀的材料，可以减少材料厚度的变化对光程差的影响。

半波损失是加半个波长还是减半
个波长
2010-01-14 23:06:36 leaves 那算劈尖干涉的时候从接触的地方开始数干涉条纹的“级数”，然后来推算条纹下面所对应的厚度，那多半个和少半个算出来的数值就不一样了呀。

（练习题，可能现实中没这么测的吧）
================================ 计算条纹级数的时候，光程差是要和尖劈接触点的光程差比较的。

没有比较的光程差是没有意义的。

光程差Δ = (n+1/2) λ 是暗条纹，光程差Δ = (n-1/2) λ 也是暗条纹，那么到底哪一个是第 n 级暗条纹？如果你规定半波损失是+λ/2，那么尖劈接触点的光程差就是Δ = +λ/2，这是第 0 级暗纹。

因此第 n 级暗条纹满足的条件是Δ = (n+1/2) λ 只有这样，当 n = 0 的时候才能退化为Δ = +λ/2。

另一方面，若该处的空气膜厚度是 d，那么Δ = 2d + λ/2 注意是+λ/2 的原因是你统一规定了半波损失是+λ/2，所以 d = n λ/2。

如果你规定半波损失是 -λ/2，那么尖劈接触点的光程差就是Δ = -
λ/2，因此第 n 级暗条纹满足的条件是Δ = (n - 1/2) λ，该处的空气膜厚度仍然是n λ/2。

结果不变。

第3节 光程和光程差双缝干涉21ϕϕ=，=∆ϕ)(212r r --λπPνλ/c =：光在真空中的波长1r ，2r ：几何路程双缝和屏之间充满一种均匀透明介质n 介质中的光速n c V /=介质中光的波长n n cV //λννλ==='=∆ϕ)(212r r -'-λπ1r 2r 3r==-'-)(212r r n n λπ)(212nr nr --λπ， 1n 2n 3n定义：光程nr =∆∑=++=∆i i r n r n r n 2211，真空中：r =∆光程差12∆-∆=δ位相差=∆ϕδλπ2-在相同时间内，若光在介质中走过的几何路程为r 则光在真空中走过的几何路程为nr 光在介质中走过r 的路程产生的位相变化=光在真空中走过nr 的路程产生的位相变化光程：光在介质中走过的路程折合成光在真空中走过的路程 例：双缝干涉 P在光路2上放一厚度 S 为t 折射率为n 的玻璃片 t n r r r nt t r )1(1212-+-=-+-=δ 2S =∆ϕδλπ2-=])1([212t n r r -+--λπλ：光在真空中的波长透镜的光程F '第4节 薄膜干涉（1）等厚干涉（2）等倾干涉一、 等厚干涉的一般理论1、 光路图 厚度不均匀薄膜2n i ：入射角 薄膜上下表面产生的两束反射光 在薄膜上表面相遇进行相干迭加32、 光程差 DC n BC AB n 12)(-+=δ，i n n e 22122sin 2-=δ312,n n n >，光线2有半波损失，光线1没有，应加上2/λ 312,n n n <，光线2没有半波损失，光线1有，应加上2/λ 321n n n <<，光线2和光线1都有半波损失， 不加2/λ 321n n n >>，光线2和光线1都没有半波损失，不加2/λ><+-=2s i n 222122λδi n n e 3、 等厚干涉条纹 i 一定，)(e δδ=⎪⎩⎪⎨⎧∈+∈>=<+-=干涉相消）（干涉加强N k k N k k i n n e 2122sin 222122λλλδk ：干涉级，k 的取值必须保证0≥e干涉条纹形状与薄膜等厚线形状相同说明：（1）用日光照射薄膜，呈现彩色条纹（2）从薄膜上方看到的是反射光的干涉 从薄膜下方看到的是透射光的干涉 透射光光程差-='sin 222122δi n n e λ一定：反射光干涉加强时，透射光干涉相消 反射光干涉相消时，透射光干涉加强 例：用日光垂直照射空气中m e μ40.0=、折射率为50.1的玻璃片 求：可见光范围，哪些波长的光反射加强、哪些波长的光透射加强？解：反射加强条件222sin 2222122λλδ+=+-=e n i n n e =λkλ=1242-k e n 3=k ，m μλ48.01321040.050.146=-⨯⨯⨯⨯=- 透射加强条件（反射光相消条件）e n i n n e 2221222sin 2=-=δ=λk ，λ=ke n 22 2=k ，m μλ60.0=；3=k ，m μλ40.0=二、 几种重要的薄膜干涉1、 劈尖干涉用波长λ的单色光垂直照射劈尖 0=i><+-=2sin 222122λδi n n e 空气劈尖22λδ+=e （空气中的玻璃劈尖22λδ+=ne ⎪⎩⎪⎨⎧=+==+=暗纹明纹,2,1,02)12(,3,2,122k k k k e λλλδ 玻璃劈尖明纹中心下面空气薄膜厚度λ412-=k e ，λ41，λ43，λ45，暗纹中心下面空气薄膜厚度λk e 21=， 0，λ1，λ，等厚线是平行棱边的直线 条纹是平行棱边的直条纹相邻两明纹或两暗纹下面空气薄膜厚度差2/λ=∆e 相邻两明纹或两暗纹的 距离θλθsin 2sin /=∆=e l 0 λ4λ2λ4λ λ4θ：劈尖的夹角，条纹均匀分布↓θ，↑l 条纹容易分辨，↑θ，↓l用途：已知λ，测量l ，求θ；已知θ，测量l ，求λ； 检验玻璃表面是否平整棱边处是一暗纹，222λλδ=+=e ，是半波损失的有力证据空气中的玻璃劈尖：n e 2λ=∆，θλsin 2n l =例：mm L 880.28=，用波长m μλ5893.0=的光垂直照射劈尖，测得第一条 明纹到第31条明纹的 距离为mm 295.4 L求：金属丝的直径D解：相邻两明纹的距离 mm l 14317.0131295.4=-=θλsin 2=l ，l 2sin λθ=l L L Ltg D 2sin λθθ=≈≈=mm 05944.0圆柱向右移动，条纹如何变化？L 条纹间距↓，向右移动 ↓L ，条纹如何变化？ 条纹间距↓)(22s i n 2/c o s /12d d tg L L N -===λθλθλθ 下面几种情况条纹如何变化？例：用波长λ的单色平行光垂直照射由平板玻璃和工件形成的空气劈尖，观察干涉条纹弯曲，弯曲部分的顶部恰与左边条纹直线部分相切，说明工件上有一凹槽，深度2/λ解；条纹是空气薄膜的等厚线 某条纹弯曲部分的顶部下面空气薄膜厚度与同一条纹上直线部分下面空气薄膜厚度相同工件上必有一凹槽，深度等于相邻两明纹直线 部分对应的空气薄膜厚度差2/λ2、 增透膜与增反膜反射光的光程差 空气1n ><+=222λδe n 薄膜2n 如果反射光干涉加强，增反膜 如果反射光干涉相消，增透膜例：设11=n ，38.12=n ，55.13=n ，用nm 550=λ的黄绿光垂直 照射薄膜，若使反射光强最小求：薄膜最小厚度解：e n 22=δe n 22=δ=2)12(λ+k λ2412n k e +=，0=k ，nm n e 10038.1455042min =⨯==λ 注：1n 、2n 、3n 、e 给定，薄膜只对特定波长的光增透或增反 若用日光照射，反射光中缺少黄绿光，反射光呈蓝紫色。

发生两次半波损失光程差-回复什么是半波损失光程差？它是如何发生两次的呢？我们将逐步回答这些问题。

半波损失光程差是指在光学器件中，由于不完美的设计或制造造成的相位偏移，导致光学传输路径长度的差异。

这种差异会引起光束的分离或衍射，从而影响光学性能。

通常，在干涉测量或光学通信系统中，此类相位偏移是不可避免的。

首先，我们将探讨为什么会发生第一次半波损失光程差。

通常，这是由于光纤的不完整折射率分布或纤芯直径不均匀而引起的。

这些不均匀导致了光传播速度的差异，从而导致光束到达目标位置时的相位偏移。

这种相位偏移可以通过精确控制光纤的制造过程来减小，以降低半波损失光程差的发生概率。

接下来，让我们来了解第二次半波损失光程差是如何发生的。

这通常是由于在光学系统的不同组件中引入了相位偏移，例如，透镜、反射镜或光波导。

这些组件可能会因为制造或使用过程中的误差而引起光程差的变化。

特别是在高精度的光学系统中，即使微小的相位偏移也可能会导致明显的光学性能下降。

那么，有哪些方法可以减小或纠正这种半波损失光程差呢？首先，制造高质量的光学器件是关键。

通过确保光纤和光学组件的准确制造和装配，可以最大程度地减小半波损失光程差。

其次，采用精确的波长校准技术，如干涉仪或频率计来检测和测量光学系统中的相位偏移。

根据测量结果，可以调整系统中的光学组件或光纤连接，以最小化光程差的影响。

此外，使用效果良好的光学补偿器件，如相位补偿片或光纤偏振控制器，可以进一步纠正光程差引起的相位偏移。

最后，让我们总结一下这个主题。

半波损失光程差是指由于光学器件中的相位偏移而引起的光传输路径长度差异。

这种现象可能会在光传输系统中发生两次。

第一次可能是由于光纤的制造不完美引起的，而第二次可能是由于光学组件的不准确制造或装配引起的。

为了减小或纠正这种光程差，我们可以采取一系列措施，包括制造高质量的光学器件、使用精确的波长校准技术以及使用补偿器件来纠正相位偏移。

总之，了解半波损失光程差的发生原因和解决方法对于光学系统的设计和优化至关重要。