光程与光程差

光程差的概念
光程差（Path Difference）是指光线通过两种不同介质时所经过的路径长度的差异。

在波动光学中，光程差是一个重要的概念，因为它决定了干涉、衍射和偏振等现象。

光程差对于理解光线如何通过介质以及如何与物质相互作用非常重要。

光程差的计算方法如下：
光程差= n1 ×Δd1 + n2 ×Δd2
其中：
n1 和n2 分别是两个介质的折射率
Δd1 和Δd2 分别是两个介质中光线所经过的路径长度差
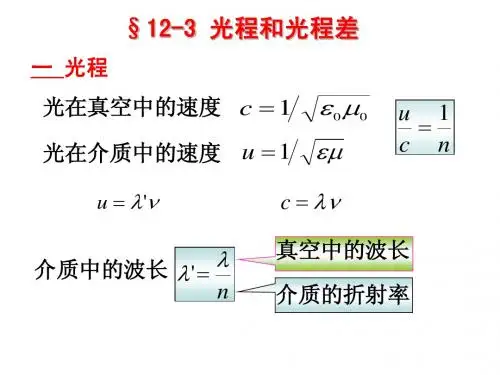
当一个光波从一种介质传播到另一种介质时，它的速度发生变化，因为光的速度等于频率乘以波长，而波长与介质的折射率有关。

当光线从一个介质进入另一个介质时，折射率发生变化，从而导致光波波长的变化。

这种波长的变化导致了光程差的出现。

1、光程与光程差：<![endif]>⑴光程：前面讨论双缝干涉时，光始终在同一种介质中传播，两相干光束在叠加点处的相位差决定于它们的波程差。

当讨论光在几种不同的介质中传播时，因光的波长与介质的折射率有关，所以同一束光在不同介质中传播相同距离时，所引起的相位变化是不同的。

可见，在不同介质中传播的两光束间的相位差与传播距离和介质折射率都有关。

设某单色光的频率为ν，在真空中的波长为λ，真空中光速为c，则有，设它在真空中传播距离d，则其相位的变化为该光束在折射率为n的介质中传播的速度为，波长为。

当它在此介质中传播距离d时，其相位的变化为可见，光在折射率为n的介质中传播距离d，相当于在真空中传播距离nd。

见下图：定义：光程定义光程的目的是将光在不同介质中实际传播的距离折算成它在真空中传播的距离。

当一束光经过若干不同介质时：光程L = S ( ni di )⑵光程差与相位差：设S1和S2为频率均为ν的相干光源，它们的初相位相同，分别在折射率为n1和n2的介质中经路程r1和r2到达空间某点P。

n2S1S2pr1r2则这两束光的光程差为相应的相位差为可见，引入光程的概念后，相位差和光程差之间的关系为⑶透镜不引起附加光程差：从物点S发出的不同光线，经不同路径通过薄透镜后会聚成为一个明亮的实像S'，说明从物点到像点，各光线具有相等的光程。

左图：平行于透镜主光轴的平行光会聚在焦点F，从波面A上各点到焦点F的光线A1F，A2F，A3F是等光程的。

中图：平行于透镜副光轴的平行光会聚于焦面F上，从波面B上各点到F'的光线B1F'，B2F'，B3F'是等光程的。

右图：点光源S发出球面波经透镜后成为会聚于像点S'的球面波，S的波面C上的各点到像点S'的光线C1S'，C2S'，C3S'是等光程的。

2、薄膜干涉的光程差公式：设一束单色光a经折射率为n，厚度为d的薄膜上、下表面的反射形成两束平行反射光a'、b'。

迈克尔逊干涉光程差公式(二)迈克尔逊干涉光程差公式1. 光程公式•迈克尔逊干涉是一种通过光程差来观察干涉现象的实验方法。

在干涉中，我们需要计算光线在两条光路中传播的光程差，即两条光路中光线的行进距离之差。

•光程公式表示了光线通过介质时的行进距离，并且与介质的折射率相关。

对于迈克尔逊干涉实验中的两条光路，它们分别通过两个不同的介质，可以使用光程公式计算它们的行进距离。

•光程公式如下所示：光程 = 折射率× 光线传播距离2. 迈克尔逊干涉光程差公式•在迈克尔逊干涉实验中，我们常常关注光程差，它表示了两条光路中光线的行进距离之差。

光程差决定了在干涉中出现明暗相间的干涉条纹。

•在迈克尔逊干涉中，对于两条光路分别为A、B，光线从光源处射出，通过分光镜分成两条路径，再通过干涉镜反射回来。

光程差公式可以表示为：光程差 = 光程A - 光程B3. 举例说明•假设我们使用迈克尔逊干涉仪测量一个薄膜的厚度。

光线从单色光源射出，经过分光镜后分成A、B两条光路，再经过干涉镜反射回来。

其中，光路A经过一层厚度为d的薄膜，折射率为n1；光路B没有经过薄膜，折射率为n2。

•我们可以利用光程差公式来计算A、B两条光路的光程差，从而得到干涉条纹的位置。

根据光程差公式：光程差 =折射率× 光线传播距离•光线在光路A中的光程为：光程A = n1 × d•光线在光路B中的光程为：光程B = n2 × d•光程差为：光程差 = 光程A - 光程B = (n1 × d) - (n2 × d) = (n1 - n2) × d•根据光程差公式，光程差与薄膜厚度d、薄膜的折射率差(n1 - n2)相关。

当光程差满足一定条件时，会出现明暗相间的干涉条纹，通过测量干涉条纹的位置，我们可以推算出薄膜的厚度。

总结•迈克尔逊干涉的光程差公式是计算干涉条纹位置的重要工具。

通过计算两条光路中光线的行进距离之差，我们可以得出干涉条纹的位置，从而推算物体的性质或参数。

光程差的计算公式
光程差是光在两条路径之间经过的距离差异。

在光学中，光程差常用于计算干涉、干涉仪和光学器件的性能。

光程差的公式可以根据特定情况和光学系统的性质来推导，以下是一些常见的光程差计算公式：
1.薄透镜的光程差公式：
光程差=(n2-n1)*d
其中，n2和n1分别是透镜两侧的介质的折射率，d是光线通过透镜的厚度。

2.双曲面透镜的光程差公式：
光程差=(n2-n1)*(R2-R1)
其中，n2和n1分别是透镜两侧的介质的折射率，R2和R1分别是透镜两表面的曲率半径。

3.光栅的光程差公式：
光程差=m*λ
其中，m是光栅的级数，λ是入射光的波长。

4.光纤的光程差公式：
光程差=(n2-n1)*L
其中，n2和n1分别是光纤芯和包层的折射率，L是光纤的长度。

5.双缝干涉的光程差公式：
光程差= d * sinθ
其中，d是两个缝的间距，θ是入射光线与法线之间的夹角。

6. Young双缝干涉的光程差公式：
光程差= d * sinθ * k
其中，d是两个缝的间距，θ是入射光线与法线之间的夹角，k是干涉级差。

这些公式给出的光程差是用于特定情形的近似计算。

在实际应用中，可以根据具体的光学系统和问题的性质，采用更复杂的公式进行光程差的计算。

光程差的计算公式光程差指的是光线在两个或多个不同介质中传播时所经过的路程差。

在光学中，光程差是一项重要的参数，它直接影响到光的干涉、衍射和折射现象等现象的产生和表现。

光程差的计算公式通常与光线在介质中的传播速度、光线的路径、反射和折射等因素有关。

下面将介绍几种常见情况下的光程差计算公式。

1.平行板间光程差：当光线从一个介质穿过一个平行板，再穿过第二个平行板，两个平行板之间的光程差可以通过以下公式来计算：光程差=(2n1d1+n2d2)-c*t其中，n1和n2分别是两个平行板的折射率，d1和d2分别是两个平行板的厚度，c是光在真空中的速度，t是光从第一个平行板到达第二个平行板所需的时间。

2.薄透镜折射光程差：当平行光线通过一个薄透镜并折射出来时，光程差可以通过以下公式来计算：光程差=(n2-n1)*r其中，n2和n1分别是透镜后面和透镜前面介质的折射率，r是光线经过透镜的距离。

3.牛顿环光程差：当光线通过凸透镜和平板玻璃组成的牛顿环时，两个相邻暗纹间的光程差可以通过以下公式来计算：光程差=2e其中，e是两个暗纹之间的半径差。

4.单缝衍射光程差：当光线通过一个狭缝并发生衍射时，光程差可以通过以下公式来计算：光程差= d*sinθ其中，d是狭缝的宽度，θ是光线与狭缝中心线的夹角。

5.双缝干涉光程差：当光线通过两个狭缝进行干涉时光程差= d*sinθ其中，d是两个狭缝的间距，θ是光线与狭缝中心线的夹角。

需要注意的是，以上公式中的折射率和反射率都是相对于真空的，实际应用中可能还需要考虑光线在介质中的衍射、散射和吸收等因素。

此外，对于复杂的光程差计算问题，可以采用光线追迹法或使用光学软件进行模拟和分析。

总之，光程差的计算公式因应用场景和物理条件的不同而有所差异，以上只是一些常见情况下的公式。

在实际应用中，需要根据具体问题进行分析和计算。

光程差的三种计算方法光程差是光学中一个非常重要的概念，它是指光线在两个点之间传播时所经过的光程差值。

在光学中，光程差是一个必须要考虑的因素，因为它会影响到光线的传播和成像效果。

在本文中，我们将介绍光程差的三种计算方法。

一、光程差的定义光程差是指光线在两个点之间传播时所经过的光程差值。

光程差可以用公式表示为：ΔL = L1 - L2其中，ΔL表示光程差，L1和L2分别表示光线从点1到点2的光程。

光程差的大小与光线传播的路径有关，因此，当光线传播路径发生变化时，光程差也会发生变化。

二、光程差的计算方法1.几何法几何法是一种简单易懂的光程差计算方法。

在几何法中，我们需要绘制出光线传播的路径，并根据路径计算出光程差。

例如，在一个透镜系统中，我们需要计算出透镜前后的光程差。

首先，我们需要绘制出透镜系统的光路图，如下图所示：图1 透镜系统的光路图在图中，P1和P2分别表示透镜的前后焦点，L1和L2分别表示光线从点1到点2的光程。

根据光程差的定义，我们可以得出透镜前后的光程差ΔL：ΔL = L2 - L1 = f2 + d - f1其中，f1和f2分别表示透镜的前后焦距，d表示透镜的厚度。

2.相位法相位法是一种基于光波相位差的计算方法。

在相位法中，我们需要测量出两个点处的光波相位差，并根据相位差计算出光程差。

例如，在一个干涉仪中，我们需要计算出两束光线的光程差。

首先，我们需要将两束光线合并在一起，使它们相干干涉，如下图所示：图2 干涉仪中的光路图在图中，L1和L2分别表示两束光线从点1到点2的光程，d表示两束光线的相位差。

根据光程差的定义，我们可以得出两束光线的光程差ΔL：ΔL = L2 - L1 = d/2πλ其中，λ表示光波的波长。

3.时间法时间法是一种基于光速和时间差的计算方法。

在时间法中，我们需要测量出两个点处的光线传播时间差，并根据时间差计算出光程差。

例如，在一个光纤系统中，我们需要计算出光纤前后的光程差。

第3节 光程和光程差双缝干涉21ϕϕ=，=∆ϕ)(212r r --λπPνλ/c =：光在真空中的波长1r ，2r ：几何路程双缝和屏之间充满一种均匀透明介质n 介质中的光速n c V /=介质中光的波长n n cV //λννλ==='=∆ϕ)(212r r -'-λπ1r 2r 3r==-'-)(212r r n n λπ)(212nr nr --λπ， 1n 2n 3n定义：光程nr =∆∑=++=∆i i r n r n r n 2211，真空中：r =∆光程差12∆-∆=δ位相差=∆ϕδλπ2-在相同时间内，若光在介质中走过的几何路程为r 则光在真空中走过的几何路程为nr 光在介质中走过r 的路程产生的位相变化=光在真空中走过nr 的路程产生的位相变化光程：光在介质中走过的路程折合成光在真空中走过的路程 例：双缝干涉 P在光路2上放一厚度 S 为t 折射率为n 的玻璃片 t n r r r nt t r )1(1212-+-=-+-=δ 2S =∆ϕδλπ2-=])1([212t n r r -+--λπλ：光在真空中的波长透镜的光程F '第4节 薄膜干涉（1）等厚干涉（2）等倾干涉一、 等厚干涉的一般理论1、 光路图 厚度不均匀薄膜2n i ：入射角 薄膜上下表面产生的两束反射光 在薄膜上表面相遇进行相干迭加32、 光程差 DC n BC AB n 12)(-+=δ，i n n e 22122sin 2-=δ312,n n n >，光线2有半波损失，光线1没有，应加上2/λ 312,n n n <，光线2没有半波损失，光线1有，应加上2/λ 321n n n <<，光线2和光线1都有半波损失， 不加2/λ 321n n n >>，光线2和光线1都没有半波损失，不加2/λ><+-=2s i n 222122λδi n n e 3、 等厚干涉条纹 i 一定，)(e δδ=⎪⎩⎪⎨⎧∈+∈>=<+-=干涉相消）（干涉加强N k k N k k i n n e 2122sin 222122λλλδk ：干涉级，k 的取值必须保证0≥e干涉条纹形状与薄膜等厚线形状相同说明：（1）用日光照射薄膜，呈现彩色条纹（2）从薄膜上方看到的是反射光的干涉 从薄膜下方看到的是透射光的干涉 透射光光程差-='sin 222122δi n n e λ一定：反射光干涉加强时，透射光干涉相消 反射光干涉相消时，透射光干涉加强 例：用日光垂直照射空气中m e μ40.0=、折射率为50.1的玻璃片 求：可见光范围，哪些波长的光反射加强、哪些波长的光透射加强？解：反射加强条件222sin 2222122λλδ+=+-=e n i n n e =λkλ=1242-k e n 3=k ，m μλ48.01321040.050.146=-⨯⨯⨯⨯=- 透射加强条件（反射光相消条件）e n i n n e 2221222sin 2=-=δ=λk ，λ=ke n 22 2=k ，m μλ60.0=；3=k ，m μλ40.0=二、 几种重要的薄膜干涉1、 劈尖干涉用波长λ的单色光垂直照射劈尖 0=i><+-=2sin 222122λδi n n e 空气劈尖22λδ+=e （空气中的玻璃劈尖22λδ+=ne ⎪⎩⎪⎨⎧=+==+=暗纹明纹,2,1,02)12(,3,2,122k k k k e λλλδ 玻璃劈尖明纹中心下面空气薄膜厚度λ412-=k e ，λ41，λ43，λ45，暗纹中心下面空气薄膜厚度λk e 21=， 0，λ1，λ，等厚线是平行棱边的直线 条纹是平行棱边的直条纹相邻两明纹或两暗纹下面空气薄膜厚度差2/λ=∆e 相邻两明纹或两暗纹的 距离θλθsin 2sin /=∆=e l 0 λ4λ2λ4λ λ4θ：劈尖的夹角，条纹均匀分布↓θ，↑l 条纹容易分辨，↑θ，↓l用途：已知λ，测量l ，求θ；已知θ，测量l ，求λ； 检验玻璃表面是否平整棱边处是一暗纹，222λλδ=+=e ，是半波损失的有力证据空气中的玻璃劈尖：n e 2λ=∆，θλsin 2n l =例：mm L 880.28=，用波长m μλ5893.0=的光垂直照射劈尖，测得第一条 明纹到第31条明纹的 距离为mm 295.4 L求：金属丝的直径D解：相邻两明纹的距离 mm l 14317.0131295.4=-=θλsin 2=l ，l 2sin λθ=l L L Ltg D 2sin λθθ=≈≈=mm 05944.0圆柱向右移动，条纹如何变化？L 条纹间距↓，向右移动 ↓L ，条纹如何变化？ 条纹间距↓)(22s i n 2/c o s /12d d tg L L N -===λθλθλθ 下面几种情况条纹如何变化？例：用波长λ的单色平行光垂直照射由平板玻璃和工件形成的空气劈尖，观察干涉条纹弯曲，弯曲部分的顶部恰与左边条纹直线部分相切，说明工件上有一凹槽，深度2/λ解；条纹是空气薄膜的等厚线 某条纹弯曲部分的顶部下面空气薄膜厚度与同一条纹上直线部分下面空气薄膜厚度相同工件上必有一凹槽，深度等于相邻两明纹直线 部分对应的空气薄膜厚度差2/λ2、 增透膜与增反膜反射光的光程差 空气1n ><+=222λδe n 薄膜2n 如果反射光干涉加强，增反膜 如果反射光干涉相消，增透膜例：设11=n ，38.12=n ，55.13=n ，用nm 550=λ的黄绿光垂直 照射薄膜，若使反射光强最小求：薄膜最小厚度解：e n 22=δe n 22=δ=2)12(λ+k λ2412n k e +=，0=k ，nm n e 10038.1455042min =⨯==λ 注：1n 、2n 、3n 、e 给定，薄膜只对特定波长的光增透或增反 若用日光照射，反射光中缺少黄绿光，反射光呈蓝紫色。

光的速度与光程差→ 电磁波的速度与光
程差
简介
本文将探讨光的速度与光程差的相关性，并将其与电磁波的速度与光程差进行比较。

以此来帮助读者更好地理解光的相关概念。

光的速度
光是电磁波的一种，它在真空中的速度被称为光速。

根据传统的物理理论，光的速度在真空中约为每秒299,792,458米。

这个速度在自然界中具有极高的意义，它对于我们认识宇宙、理解光的传播等方面有重要作用。

光程差
光程差是光线从一个点传播到另一个点所经历的路径差。

它是光线传播的一个重要物理量。

当光通过不同介质（如空气、水、玻璃等）时，由于介质的折射作用，光线在传播过程中会发生偏离，导致光程差的产生。

光程差的大小与光速、介质的折射率以及两个传播点之间的距离有关。

电磁波的速度与光程差
光是电磁波的一种，而电磁波的速度与光程差的概念也与光相似。

电磁波的速度是其在真空中的传播速度，也是光速。

而电磁波在介质中传播时，同样会发生偏离，产生光程差。

需要注意的是，不同频率下的电磁波在介质中的速度与光程差可能会有所不同。

这是因为不同频率的电磁波在介质中的折射率不同，导致其传播速度和光程差也有所变化。

结论
光的速度与光程差是光传播过程中重要的物理量。

它们也同样适用于电磁波的传播。

光的速度在真空中为光速，而光程差受到介质折射率和传播距离的影响。

对于电磁波来说，其速度与光一样，但在不同介质中传播时，也会出现光程差的现象。

了解光的速度与光程差的概念，有助于我们更好地理解光传播以及电磁波在介质中的行为。

这对于相关领域的研究和应用具有重要意义。