大学物理 相位差和光程

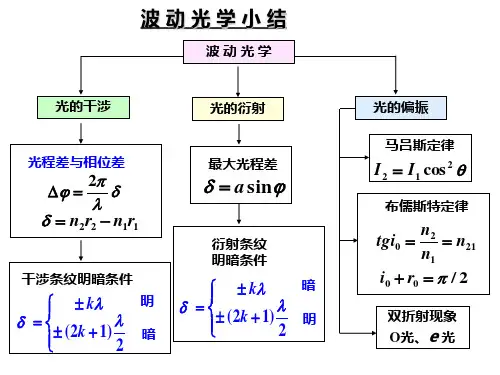
第十四章波动光学一、基本要求1. 掌握光程的概念以及光程差和相位差的关系。

2. 理解获得相干光的方法，能分析确定杨氏双缝干涉条纹及薄膜等厚干涉条纹的位置，了解迈克尔逊干涉仪的工作原理。

3. 了解惠更斯-菲涅耳原理; 掌握用半波带法分析单缝夫琅和费衍射条纹的产生及其明暗纹位置的计算，会分析缝宽及波长对衍射条纹分布的影响。

4. 掌握光栅衍射公式。

会确定光栅衍射谱线的位置。

会分析光栅常数及波长对光栅衍射谱线分布的影响。

5. 了解自然光和线偏振光。

理解布儒斯特定律和马吕斯定律。

理解线偏振光的获得方法和检验方法。

6. 了解双折射现象。

二、基本内容1. 相干光及其获得方法只有两列光波的振动频率相同、振动方向相同、振动相位差恒定时才会发生干涉加强或减弱的现象，满足上述三个条件的两束光称为相干光。

相应的光源称为相干光源。

获得相干光的基本方法有两种：（1）分波振面法（如杨氏双缝干涉、洛埃镜、菲涅耳双面镜和菲涅耳双棱镜等）；（2）分振幅法（如薄膜干涉、劈尖干涉、牛顿环干涉和迈克耳逊干涉仪等）。

2. 光程和光程差（1）光程把光在折射率为n的媒质中通过的几何路程r折合成光在真空x中传播的几何路程x，称x为光程。

nr（2）光程差在处处采用了光程概念以后就可以把由相位差决定的干涉加强，减弱等情况用光程差来表示，为计算带来方便。

即当两光源的振动相位相同时，两列光波在相遇点引起的振动的位相差πλδϕ2⨯=∆ （其中λ为真空中波长，δ为两列光波光程差） 3. 半波损失光由光疏媒质（即折射率相对小的媒质）射到光密媒质发生反射时，反射光的相位较之入射光的相位发生了π的突变，这一变化导致了反射光的光程在反射过程中附加了半个波长，通常称为“半波损失”。

4. 杨氏双缝干涉经杨氏双缝的两束相干光在某点产生干涉时有两种极端情况：（1）位相差为0或2π的整数倍，合成振动最强；（2）位相差π的奇数倍，合成振动最弱或为0。

其对应的光程差()⎪⎩⎪⎨⎧-±±=212λλδk k ()()最弱最强 ,2,1,2,1,0==k k 杨氏的双缝干涉明、暗条纹中心位置：dD k x λ±= ),2,1,0( =k 亮条纹 d D k x 2)12(λ-±= ),2,1( =k 暗条纹 相邻明纹或相邻暗纹间距:λd D x =∆ （D 是双缝到屏的距离，d 为双缝间距） 5. 薄膜干涉以21n n <为例，此时反射光要计“半波损失”， 透射光不计“半波损失”。

光相位公式
相位差=2π/λ×光程差（λ为真空中的波长）。

光程差定义为两束光到达某点的光程之差值，是表明干涉条纹性质的量。

是指由不同点发出的相干光在到达叠合点(承光板)时,两光线行程距离的差数(同一种介质中，对不同的介质还要考虑折射率的影响）。

对于两同相的相干光源发出的两相干光，其干涉条纹的明暗条件便可由两光的光程差Δ决定。

光程差的计算有两项，一项是几何路程差引起的；另一项要考虑反射面情况，当光线从光疏介质射向光密介质时，反射光有半波损失，其他情况都没有。

相位传输与光程差的关系全文共四篇示例，供读者参考第一篇示例：相位传输与光程差的关系是光学中一个非常重要的概念。

在光学中，光波的传播可以采用波动模型来描述。

而相位传输和光程差则是描述光波在传播过程中的一个重要参数。

本文将从相位传输和光程差的概念入手，探讨它们之间的关系。

首先，我们来解释一下什么是相位传输和光程差。

在光学中，相位是用来描述波的状态的一个物理量，它是一个关于时间和空间的函数。

光波在传播过程中，相位传播就是描述波前的传播方向和速度，而光程差则是描述波在传播过程中经过的路径长度差异。

光程差和相位传输之间的关系可以通过波动方程来解释。

在光学中，光波的传播可以用亥姆霍兹方程来描述：∇²E + k²E = 0其中，E是电场的复振幅，∇是梯度算子，k是波数，其定义为k=2π/λ，λ是波长。

这个方程描述了光波在介质中的传播。

在自由空间中，k=k0=2π/λ0，λ0表示真空中的波长。

根据亥姆霍兹方程，我们可以得到波动方程：E(x,t) = Aexp(i(kx-ωt))其中，A是振幅，i是虚数单位，k是波数，ω是角频率。

这个方程描述了光波在空间和时间上的特性。

通过这个方程，我们可以看到，相位传输和光程差之间的关系是密切相关的。

假设光波在传播过程中经过了一段光程差ΔL。

光波的相位传输Δθ可以表示为：Δθ = kΔL根据光程差的定义，可以得到：ΔL = nΔd其中，n是介质的折射率，Δd是光波在介质中传播的路径长度。

将光程差代入相位传输的公式中，可以得到：Δθ = nkΔd这个公式表明了相位传输和光程差之间的关系。

可以看到，光程差越大，相位传输也会随之增大。

这是因为在光学中，路径长度的增加会导致相位的改变。

因此，相位传输和光程差之间存在着紧密的关联。

在实际的光学实验中，相位传输和光程差的关系可以用来解释一些光学现象。

例如，在干涉实验中，两路光波的相位差可以通过光程差来计算。

在多束干涉中，由于不同光束走过路径不同，因此相位传输和光程差之间的关系非常重要。

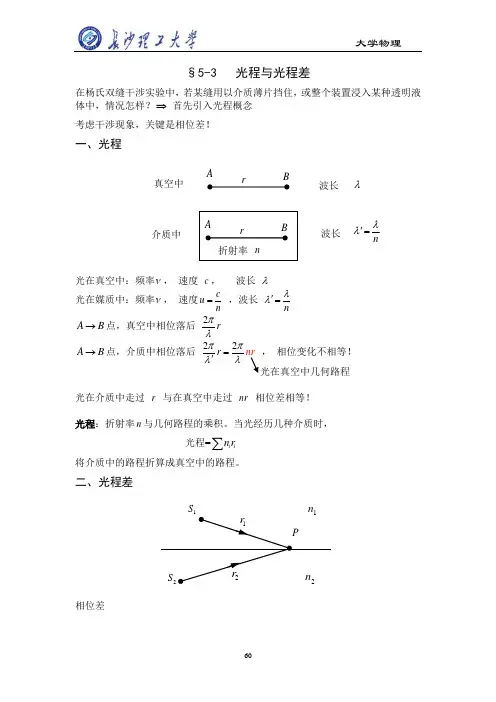
§5-3 光程与光程差在杨氏双缝干涉实验中，若某缝用以介质薄片挡住，或整个装置浸入某种透明液体中，情况怎样？⇒ 首先引入光程概念 考虑干涉现象，关键是相位差！一、光程光在真空中：频率ν， 速度 c ， 波长 λ光在媒质中：频率ν， 速度c u n = ，波长 n λλ'=A B →点，真空中相位落后2r πλ A B →点，介质中相位落后 22r nr ππλλ=' ， 相位变化不相等！ 光在真空中几何路程光在介质中走过 r 与在真空中走过 nr 相位差相等！光程：折射率n 与几何路程的乘积。

当光经历几种介质时， 光程=i i n r ∑ 将介质中的路程折算成真空中的路程。

二、光程差相位差ABrABrn真空中介质中折射率 波长λ波长 nλλ'=1S 2S P2r 1r 2n 1()2010212122r r ππϕϕϕλλ⎛⎫∆=--- ⎪⎝⎭()2010221122n r n r ππϕϕλλ⎛⎫=---⎪⎝⎭()()2010201022n r n r ππϕϕϕϕλλ=---=--∆光程差 2211n r n r ∆=- 设两个光源同相位 20100ϕϕ-= 即2πϕλ∆=-∆真空中的波长 由相长和相消条件2k ϕπ∆=± （0,1,2,k =） 干涉相长 (21)k ϕπ∆=±+ （0,1,2,k =） 干涉相消可得22kλ∆=± （0,1,2,k =） 干涉相长 (21)2k λ∆=±+ （0,1,2,k =） 干涉相消在分析问题时，只需要考虑光程，注意λ为真空中波长。

好处：统一用真空波长表达相位的变化。

三、薄透镜的等光程性在光学中经常用到透镜，需要指出的是透镜不附加光程差。

abcF亮点A B CAF 、BF 和CF 三条光线几何路程不等，但光程相等！透镜不附加光程差！（不证）二、双缝干涉实验的讨论1、光源移动光源下移：光源在S 时，0P （0级亮）： 210r r -=光源在S '时，0P '（0级亮）： ()()22110R r R r +-+= 1221R R r r -=-下移： 12R R > ， 21r r > （0级亮纹上移，条纹宽度不变）()()0201212r r πϕϕϕλ∆=---()()212122R R r r ππλλ=---- （1S 和2S 光源初相差0≠）()2122dR R x Dππλλ=---思考：光源向上移动？abcF亮点A B C'F δ2r 1R θ1s 2s Ddop '中央亮纹s s '1r 2R o p zyx上下移动光源，S 的移动方向与条纹的移动方向相反，条纹宽度不变！ 2、改变双缝间距dD x dλ∆=d ↑ ，x ∆↓ ，条纹变密 （当 d 大到一定程度，条纹密不可分，一个亮带，无干涉）3、将一缝的宽度稍增加一点12I I ≠： min 0I ≠，暗条纹处有一定光强，条纹衬比度变差。

相位传输与光程差的关系
相位传输和光程差是光学中两个重要的概念，它们之间有着密
切的关系。

首先，我们来解释一下这两个概念。

相位传输是指光波在传播过程中所积累的相位变化。

光波在传
播过程中会受到介质折射率的影响，从而导致光波的相位发生变化。

相位传输可以用来描述光波在空间中的传播情况，对于干涉、衍射
等现象都有着重要的作用。

光程差是指光波在不同路径上传播所积累的光程差异。

在光学
系统中，光波会经过不同的光程，由于介质的折射率不同或者光路
长度不同，导致光波到达某一点时所积累的光程不同，这就是光程差。

那么，相位传输和光程差之间的关系是什么呢？在光学中，光
程差可以用相位差来表示，即光程差等于相位差除以波数。

波数是
一个与光波的波长有关的物理量，通常用2π除以波长来表示。

因此，光程差与相位差之间存在着简单的线性关系。

在干涉现象中，光程差对于干涉条纹的形成起着至关重要的作
用。

通过调节光程差，可以改变干涉条纹的位置和形状。

而相位传
输则可以帮助我们理解光波在传播过程中的相位变化规律，从而更
深入地理解干涉、衍射等现象。

总之，相位传输和光程差是光学中两个重要的概念，它们之间
存在着密切的关系。

相位传输描述了光波在传播过程中的相位变化，而光程差则描述了光波在不同路径上传播所积累的光程差异。

它们
共同影响着光学现象的产生和演变。

希望这个回答能够帮助你更好
地理解相位传输和光程差之间的关系。

相位差和光程差嘿，咱今儿就来唠唠相位差和光程差这俩玩意儿。

你看啊，咱就说这相位差，就好像是两个人跑步，一个跑得快，一个跑得慢，那他们之间的差距就是相位差。

光程差呢，就像是两个人走的路不一样长，这路的长短差别就是光程差啦。

有一次我和几个朋友在那讨论这事儿呢。

“哎呀，这相位差到底是啥意思呀？”一个朋友挠着头问。

我笑着说：“你就想啊，就像咱俩同时开始做一件事，你做得快，我做得慢，咱俩进度不一样，这就是相位差嘛。

”“哦，原来是这样啊，那光程差呢？”他接着问。

另一个朋友抢着说：“这光程差就好比咱俩从不同地方出发去一个地方，咱俩走的路长度不一样呗。

”“嘿，你这解释还挺形象！”大家都笑了起来。

咱再深入说说啊，这相位差在很多地方都可重要啦。

比如说在波动现象里，那可有着关键的作用呢。

就像音乐会里，各种乐器发出的声音，它们之间就存在着相位差，这样才让音乐变得丰富多彩呀。

光程差呢，在光学里那也是不能小瞧的。

想想那些漂亮的彩虹，就是因为光程差的存在才有了那么多颜色呢。

咱平时生活里其实也能感觉到这些。

就像有时候你看两个东西在动，它们好像有点不一样的节奏，这其实也有点相位差的感觉呢。

我觉得啊，理解相位差和光程差就像是打开了一扇通往奇妙世界的门。

它们让我们看到了那些隐藏在日常背后的奇妙规律和现象。

我们可以通过它们更好地理解这个世界，从微小的波动到宏大的光学现象。

所以说啊，可别小瞧了这相位差和光程差，它们虽然看不见摸不着，但却在很多地方都起着至关重要的作用呢。

它们就像是隐藏在世界背后的小秘密，等着我们去发现和探索呀。

光程差和相位关系嘿，朋友！咱们今天来聊聊光程差和相位关系，这俩家伙可神秘又有趣着呢！你想想，光就像个调皮的小精灵，在不同的介质里穿梭，速度还不一样。

这就引出了光程差这个概念。

光程差啊，简单说就是两束光走过的路程的差别。

比如说，你和朋友去参加跑步比赛，同样的时间，你在平坦的大道上跑，他在坑坑洼洼的小路上跑。

最后到达终点，你们跑过的距离能一样吗？光也是这样，在不同的环境里，走的路程就有了差别，这就是光程差。

那相位又是什么呢？相位就像是光的“步伐”。

光在振动的时候，有自己的节奏和位置。

两束光如果相位相同，就像是两个人步伐一致，一起向前走；要是相位不同，就好比一个人快一个人慢，就不协调啦。

光程差和相位关系密切得很呢！光程差的变化会直接影响相位。

这就好比你在爬山，爬得越高，看到的风景就不一样。

光程差变了，相位也就跟着变啦。

假如有两束光，它们的光程差是半个波长，那它们的相位就相差180 度，就像两个方向相反的箭头。

要是光程差是一个波长，那相位就相同啦，就像两个同向的箭头，一起往前冲。

你再想想，舞台上的灯光，为什么能变幻出那么多美丽的色彩和图案？不就是因为光程差和相位的巧妙变化嘛！光程差和相位关系在生活中的应用也不少呢！比如在光学仪器里，像显微镜、望远镜，都得靠它们来让我们看清微小的东西或者遥远的星星。

还有啊，在通信领域，光信号的传输也离不开对光程差和相位关系的精准控制。

不然，咱们的电话、网络怎么能那么顺畅地传递信息呢？所以说，光程差和相位关系可不是什么抽象的概念，它们就在我们身边，影响着我们的生活。

咱们得好好理解它们，才能更好地感受这个神奇的光的世界！总之，光程差和相位关系就像一对亲密的伙伴，相互影响，共同为我们展现出光的奇妙之处。

朋友，你是不是对它们有了更深的认识呢？。

12.1.3光程与光程差的计算在分析和讨论光的干涉过程时，必须考虑光在不同介质中传播的问题，例如光穿过透镜时的情况。

由于光在不同介质中的波速和波长不相同，光干涉的情况比前面在机械波中的讨论要复杂一些。

一、光程和光程差先分析光的波长在介质中变化的情况。

介质的折射率定义为真空光速与介质中光速的比，故有其中λ表示光在真空中的波长，表示介质中的波长。

由于，所以即光在介质中的波长比真空中的波长要短一些。

下面分析一束光在介质中传播时光振动的相位差。

设有一束光在空间传播，沿光线设立x轴，A和B为x轴上两点，光在A B之间的路程（波程）为x，即B点比A点距离波源要远x这么一段长度，见下图（a）。

若A B之间是真空或空气，则A B之间光振动的时间差，即B点的光振动比A点在时间上要落后；A B之间光振动的相位差，即B点比A点在相位上要落后，其中λ为光在真空中的波长。

若A B之间是折射率为n的介质，见下图（b），则A B之间光振动的时间差，相位差，其中为介质中的波长，可见相位差不仅和波程x相关，还与折射率有关。

若A B之间有几种不同的介质，其长度分别为、、…折射率分别为、、…，见下图（c），则A B之间的时间差为，相位差为，其中λ为真空中的波长。

光程的概念定义A B之间的光程为求和沿光线（光路）进行，则A B之间光振动的时间差可简洁表示为相位差为在形式上又回到了“真空”情况。

光程显然和波程不同，光程含有波程和折射率两个因数，除非在光路上全是真空或空气，光程大于波程。

在物理意义上，光程的概念有等价折算的含义。

例如，有3/4毫米长折射率为4/3的一层水膜，有2/3毫米折射率为3/2的一块玻璃片，这两个物体在很多方面性质都不同，如力学性质、热学性质、电学性质等等。

但它们的光程相同（1毫米），这意味着光通过它们时所需要的时间，以及由此产生的相位差相同，都相当于1毫米的真空。

在引起光振动的时间差和相位差方面，它们完全等价，或者通俗地说，是不可分辨的。