主成分回归分析方法

主成分回归分析
logistic 回归分析法是一种应用最大似然法估计回归系数的回归方法,它不要求变量服从协方差矩阵相等和残差项服从正态分布,因而得到广泛的应用。

logistic 回归要求模型的解释变量之间不能具有线性的函数关系,然而, 在很多研究中, 各变量常常不是独立存在的, 而是存在一定程度的线性依存关系, 这一现象称作多重共线性(multi-collinearity。

多重共线性关系常增大估计参数的标准误,从而降低模型的稳定性,有时还可出现与实际情况相悖的结果。

因此, 为了合理地估计和解释一个回归模型, 需要对变量之间的多重共线性进行处理。

主成分 logistic 回归是解决 logistic 回归分析中的共线性问题的常用方法之一, 它通过主成分变换,将高度相关的变量的信息综合成相关性低的主成分, 然后以主成分代替原变量参与回归。

原理与步骤
1、原始数据标准化
2、计算相关系数矩阵
3、求相关矩阵 R 的特征根、特征向量和方差贡献率,确定主成分。

4、建立主成分特征函数
5、使用主成分代替原始变量进行多元回归。

近红外反射光谱法-土壤性质的主成分回归分析摘要一个快速，便捷的土壤分析技术是需要土壤质量评价和精密的土壤管理。

本研究的主要目的是评估近红外反射光谱（NIRS）来预测不同土壤性质的能力。

从Perstrop近红外系统6500扫描单色仪（福斯NIRSystems，马里兰州Silver Spring），和33种化学、物理和生物化学特性得到近红外反射光谱，从四个主要土地资源收集区802土壤样品（MLRAs）进行了研究。

定标是基于在1300到2500nm光谱范围内使用光学密度一阶导数[log(1/ R )]得主成分回归。

全部的碳、氮、湿度、阳离子交换量（CEC）、1.5兆帕水、基础呼吸速率、沙、淤泥和Mehlich III可萃取钙通过近红外光谱（r2>0.80）成功地预测。

有些Mehlich III可萃取金属（铁，钾，镁，锰）、可交换阳离子（钙，镁，钾），可交换基地、交换性酸、粘土、潜在可矿化氮、总呼吸速率、生物量碳和pH值的总和也可通过近红外光谱估计，但精度较低(r 2=0.80~0.50)。

聚合（wt％>2，1，0.5，0.25mm，并宏观聚合）的预测结果是不可靠的（r2=0.46~0.60）。

Mehlich III提取的Cu，P和Zn和交换性钠不能使用NIRS-PCR技术（r2<0.50）进行预测。

结果表明，NIRS可以作为一种快速的分析技术，在很短的时间用可接受的准确度来同时估计多个土壤特性。

测量土壤性质的标准程序是复杂的、耗时的，而且费用昂贵。

在农民和土地管理者将能够充分利用测土作为精准农业与土壤质量的评估和管理的一种辅助手段之前，一种快速、经济的土壤分析技术是需要。

近红外反射光谱技术是一种为研究入射光和材料表面之间相互作用的非破坏性的分析技术。

由于其简单性、快速性，并且需要很少或无需样品制备，近红外反射光谱被广泛用于工业。

三十多年以前，该技术最早用于粮食的快速水汽分析。

现在，近红外光谱是用于粮食和饲料质量评估的主要分析技术。

主成分分析（principal components analysis，PCA）又称：主分量分析，主成分回归分析法什么是主成分分析法主成分分析也称主分量分析，旨在利用降维的思想，把多指标转化为少数几个综合指标。

在统计学中，主成分分析（principal components analysis,PCA）是一种简化数据集的技术。

它是一个线性变换。

这个变换把数据变换到一个新的坐标系统中，使得任何数据投影的第一大方差在第一个坐标(称为第一主成分)上，第二大方差在第二个坐标(第二主成分)上，依次类推。

主成分分析经常用减少数据集的维数，同时保持数据集的对方差贡献最大的特征。

这是通过保留低阶主成分，忽略高阶主成分做到的。

这样低阶成分往往能够保留住数据的最重要方面。

但是，这也不是一定的，要视具体应用而定。

[编辑]主成分分析的基本思想在实证问题研究中，为了全面、系统地分析问题，我们必须考虑众多影响因素。

这些涉及的因素一般称为指标，在多元统计分析中也称为变量。

因为每个变量都在不同程度上反映了所研究问题的某些信息，并且指标之间彼此有一定的相关性，因而所得的统计数据反映的信息在一定程度上有重叠。

在用统计方法研究多变量问题时，变量太多会增加计算量和增加分析问题的复杂性，人们希望在进行定量分析的过程中，涉及的变量较少，得到的信息量较多。

主成分分析正是适应这一要求产生的，是解决这类题的理想工具。

同样，在科普效果评估的过程中也存在着这样的问题。

科普效果是很难具体量化的。

在实际评估工作中，我们常常会选用几个有代表性的综合指标，采用打分的方法来进行评估，故综合指标的选取是个重点和难点。

如上所述，主成分分析法正是解决这一问题的理想工具。

因为评估所涉及的众多变量之间既然有一定的相关性，就必然存在着起支配作用的因素。

根据这一点，通过对原始变量相关矩阵内部结构的关系研究，找出影响科普效果某一要素的几个综合指标，使综合指标为原来变量的线性拟合。

主成分分析法的原理和步骤主成分分析（Principal Component Analysis，简称PCA）是一种常用的多元统计分析方法，它通过线性变换将高维数据转换为低维数据，从而实现降维和数据可视化。

PCA的基本思想是通过选取少数几个主成分，将原始变量的方差最大化，以便保留大部分的样本信息。

下面我将详细介绍PCA的原理和步骤。

一、主成分分析的原理主成分分析的核心原理是将n维的数据通过线性变换转换为k维数据（k<n），这k维数据是原始数据最具有代表性的几个维度。

主成分是原始数据在新坐标系中的方向，其方向与样本散布区域最大的方向一致，而且不同主成分之间互不相关。

也就是说，新的坐标系是通过原始数据的协方差矩阵的特征值分解得到的。

具体来说，假设我们有一个m个样本、维度为n的数据集X，其中每个样本为一个n维向量，可以表示为X=\left ( x_{1},x_{2},...,x_{m} \right )。

我们的目标是找到一组正交的基变量（即主成分）U=\left ( u_{1},u_{2},...,u_{n} \right )，使得原始数据集在这组基变量上的投影方差最大。

通过对协方差矩阵的特征值分解，可以得到主成分对应的特征向量，也就是新的基变量。

二、主成分分析的步骤主成分分析的具体步骤如下：1. 标准化数据：对于每一维度的数据，将其减去均值，然后除以标准差，从而使得数据具有零均值和单位方差。

标准化数据是为了消除不同维度上的量纲差异，确保各维度对结果的影响是相等的。

2. 计算协方差矩阵：对标准化后的数据集X，计算其协方差矩阵C。

协方差矩阵的元素c_{ij}表示第i维度与第j维度之间的协方差，可以用以下公式表示：\[c_{ij}=\frac{\sum_{k=1}^{m}\left ( x_{ik}-\bar{X_{i}} \right )\left( x_{jk}-\bar{X_{j}} \right )}{m-1}\]其中，\bar{X_{i}}表示第i维度的平均值。

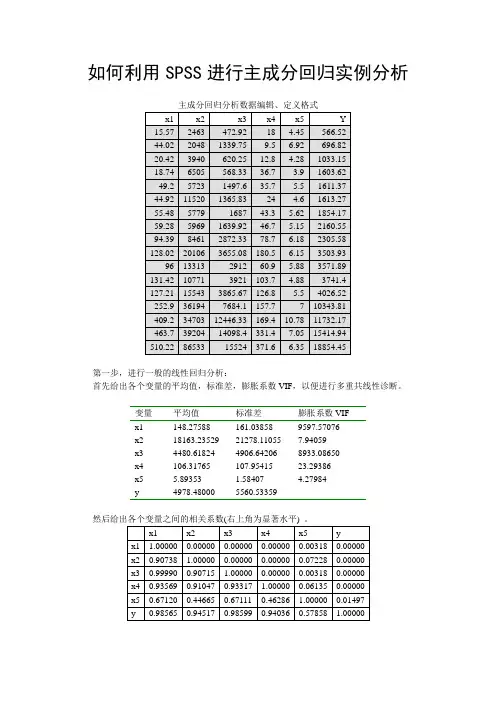
如何利用SPSS进行主成分回归实例分析主成分回归分析数据编辑、定义格式第一步，进行一般的线性回归分析：首先给出各个变量的平均值，标准差，膨胀系数VIF，以便进行多重共线性诊断。

变量平均值标准差膨胀系数VIFx1 148.27588 161.03858 9597.57076x2 18163.23529 21278.11055 7.94059x3 4480.61824 4906.64206 8933.08650x4 106.31765 107.95415 23.29386x5 5.89353 1.58407 4.27984以及一般线性回归模型分析结果：方差分析表方差来源平方和df 均方F值显著水平回归490177488.12165 5 98035497.62433 237.79008 0.00000剩余4535052.36735 11 412277.48794总的494712540.48900 16 30919533.78056相关系数R=0.995406，决定系数RR=0.990833，调整相关R'=0.993311变量x 回归系数标准系数偏相关标准误t值显著水平b0 1962.94803 1071.36166 1.83220 0.09184 b1 -15.85167 -0.45908 -0.04888 97.65299 -0.16233 0.87375 b2 0.05593 0.21403 0.62148 0.02126 2.63099 0.02194 b3 1.58962 1.40269 0.15318 3.09208 0.51409 0.61652 b4 -4.21867 -0.08190 -0.17452 7.17656 -0.58784 0.56754 b5 -394.31413 -0.11233 -0.49331 209.63954 -1.88091 0.08446 剩余标准差sse=642.08838，Durbin-Watson d=2.73322。

主成分回归（Principal Component Regression）主成分回归是一种结合了主成分分析（Principal Component Analysis，PCA）和线性回归的统计方法。

它的目标是通过将自变量进行降维，并利用主成分来解释自变量之间的相关性，从而提高回归模型的性能。

关键概念主成分分析（PCA）主成分分析是一种常用的降维技术，它通过线性变换将原始数据映射到新的坐标系中，使得新坐标系下的数据具有最大的方差。

这些新坐标被称为主成分，它们按照方差的大小排序。

主成分可以看作是原始数据中最重要的特征或信息。

线性回归线性回归是一种常见的统计方法，用于建立自变量和因变量之间线性关系的模型。

线性回归模型可以表示为：Y = β0 + β1X1 + β2X2 + … + βnXn + ε，其中Y是因变量，X1、X2、…、Xn是自变量，β0、β1、β2、…、βn是回归系数，ε是误差项。

主成分回归主成分回归将主成分作为自变量代替原始自变量，并利用线性回归建立主成分与因变量之间的关系。

主成分回归的基本思想是通过降维去除自变量之间的相关性，从而减少多重共线性对线性回归模型的影响，提高模型的稳定性和预测能力。

重要性和应用降维主成分回归通过主成分分析将自变量进行降维处理，减少了自变量的数量，简化了模型的复杂度。

降维可以帮助我们更好地理解数据，并提高模型的解释能力。

降维还可以减少计算资源的消耗，并加快模型训练和预测的速度。

处理多重共线性多重共线性是指自变量之间存在高度相关关系，导致线性回归模型估计结果不稳定或不可靠。

主成分回归可以通过降维去除自变量之间的相关性，减少多重共线性对模型的影响。

它将自变量转化为一组无关或弱相关的主成分，从而提高模型的稳定性和可靠性。

模型优化主成分回归可以通过选择合适数量的主成分来优化模型。

选择过多的主成分可能会引入噪声和不必要的复杂性，而选择过少的主成分可能会丢失重要信息。

通过交叉验证等方法，可以选择最佳的主成分数量，从而提高模型的预测能力。

主成分回归模型主成分回归模型是一种线性回归模型，用于通过消除多重共线性和记录数据的维度减少，以解释变量之间的关系。

它的思想源自于因子分析的概念，其基本思想是通过最大化方差来将原始观测变量重新组合，以获得较低维度的主成分。

它以其独特的方式对变量进行线性组合以表示数据，并消除共线性，从而可用于建立变量之间的线性关系模型。

主成分回归模型最初发布于1976年，由Harman和Hooks提出。

它是最初由Harman和Hook发明的，但是由Recknagel和Tatsuoka发展而成，他们提出了一个假设解释变量之间的关系的方法。

主成分回归模型的假设是，原始观测变量可以重新组合以形成更低维度的主成分，通过这种方式来表示变量之间的线性关系模型。

它为回归分析中的多重共线性提供了一种有效的解决方案，弥补了其他回归技术无法有效解决的问题。

主成分回归模型的主要优点是，它可以有效消除对变量之间的关系影响的多重共线性，并可以有效利用原始变量之间的冗余信息，同时保持可解释性和可操作性。

这也是主成分回归模型的核心优势之一。

另外，主成分回归模型的变量组合也可以提高模型的拟合能力，以更准确地表示数据，并减少回归模型中的随机误差。

另外，由于主成分回归模型旨在消除多重共线性，因此它可以有效地处理大规模数据集中的高维数据。

事实上，它具有提取具有最大方差的主成分的能力，因此可以大大减少记录数据的维度。

主成分回归模型的主要缺点是它不可以用于非线性关系模型，因为它只能处理基于线性关系的数据。

另外，它也无法有效地处理协变量之间的交互效应，因为它不能捕捉这种关系。

总的来说，主成分回归模型是一种有用的分析工具，可以有效消除多重共线性，提高可解释性，减少记录数据的维度，以及提高模型的拟合能力。

它已成为许多学者和其他专业人员在数据分析中的一种重要方法，用于研究变量之间的关系。

主成分分析法的原理和步骤
主成分分析（Principal Component Analysis，PCA）是一种常用的降维技术，主要用于数据预处理和特征提取。

其原理是通过线性变换将原始数据转换为具有特定性质的新坐标系，使得转换后的坐标系上数据的方差最大化。

主成分分析的步骤如下：
1. 标准化数据：对原始数据进行标准化处理，即对每个特征进行零均值化。

这是为了消除不同量纲的影响。

2. 计算协方差矩阵：计算标准化后的数据的协方差矩阵。

协方差矩阵描述了不同特征之间的相关性。

3. 计算特征值和特征向量：对协方差矩阵进行特征值分解，得到特征值和对应的特征向量。

特征值表示新坐标系上每个特征的方差，而特征向量则表示原始特征在新坐标系上的投影。

4. 选择主成分：按照特征值的大小排序，选择前k个特征值对应的特征向量作为主成分。

选择的主成分应该能够解释数据中大部分的方差。

5. 构造新的特征空间：将选择的主成分组合起来，构成新的特征空间。

这些主成分通常被视为数据的“重要”特征，用于表示原始数据。

通过主成分分析，可以将原始数据降维到低维度的子空间上，并且保留了原始数据中的信息。

这样做的好处是可以减少数据维度，简化模型，降低计算复杂度。

同时，通过选择合适的主成分，还可以实现数据的压缩和特征的提取。

主成分回归分析及其在统计学中的应用主成分回归分析是一种常用的统计学方法，用于处理多个自变量与一个因变量之间的关系。

它结合了主成分分析和多元线性回归分析的优点，能够降低自变量的维度，并提取出最能解释因变量变异的主成分。

本文将介绍主成分回归分析的基本原理和应用，并探讨其在统计学中的重要性。

一、主成分回归分析的基本原理主成分回归分析的基本原理是通过主成分分析将多个自变量转化为一组无关的主成分，然后利用这些主成分进行回归分析。

其步骤如下：1. 收集数据：首先需要收集包含多个自变量和一个因变量的数据集。

2. 主成分分析：利用主成分分析方法对自变量进行降维，得到一组无关的主成分。

主成分是原始自变量的线性组合，能够解释原始自变量变异的大部分信息。

3. 回归分析：将主成分作为新的自变量，利用多元线性回归模型进行建模，得到主成分回归方程。

4. 解释结果：通过分析主成分回归方程的系数和显著性水平，解释自变量对因变量的影响。

二、主成分回归分析的应用主成分回归分析在统计学中有着广泛的应用，以下将介绍其中几个重要的应用领域。

1. 经济学：主成分回归分析可以用于经济数据的分析和预测。

例如，可以利用主成分回归分析来分析不同经济指标对国内生产总值的影响，从而预测经济增长趋势。

2. 金融学：主成分回归分析可用于资产组合的风险管理。

通过将多个资产的收益率转化为主成分，可以降低投资组合的维度，并提取出最能解释收益率变异的主要因素，从而帮助投资者进行有效的资产配置。

3. 市场调研：主成分回归分析可以用于市场调研数据的分析。

通过将多个市场调研指标转化为主成分，可以减少指标之间的相关性，并提取出最能解释市场变异的主要因素，从而帮助企业了解市场需求和消费者行为。

4. 医学研究：主成分回归分析可用于医学研究中的变量选择和模型建立。

通过将多个生理指标转化为主成分，可以降低指标的维度，并提取出最能解释疾病变异的主要因素，从而帮助医生进行疾病诊断和治疗。

主成分回归步骤：（假设有一个因变量y ，五个自变量12345,,,,x x x x x ）
（法一）
1、主成分分析
通过“累积贡献率”和“因子负荷阵”，确定主成分的个数，比如2个 同时，计算“因子得分”，其中因子的有Fac1, Fac2
则主成分为：（利用等式计算两个主成分）
2、主成分回归
①用因变量y ，两个主成分prin1,prin2作为自变量，做二元线性回归模型，得到回归方程
②以prin1为因变量，与原来的五个自变量做多元线性回归模型，得到回归方程
③以prin2为因变量，与原来的五个自变量做多元线性回归模型，得到回归方程
将②③得到的回归方程代入①的回归方程，消去prin1,prin2,就会得到最终的y 与五个自变量的主成分回归模型。

（法二）此法没有求出主成分
1、主成分分析
通过“累积贡献率”和“因子负荷阵”，确定主成分的个数，比如2个 同时，计算“因子得分”，其中因子的有Fac1, Fac2
2、主成分回归
①用因变量y ，两个因子Fac1, Fac2作为自变量，做二元线性回归模型，得到回归方程
②以Fac1为因变量，与原来的五个自变量做多元线性回归模型，得到回归方程 ③以Fac2为因变量，与原来的五个自变量做多元线性回归模型，得到回归方程 将②③得到的回归方程代入①的回归方程，消去Fac1, Fac2,就会得到最终的y 与五个自变量的主成分回归模型。

主成分回归法-回复主成分回归法（Principal Component Regression，PCR）是一种常用于多元回归分析的统计方法。

它结合了主成分分析和普通最小二乘法回归的优点，能够处理高维数据和共线性问题，并提高回归模型的预测能力。

在进行PCR之前，首先需要准备数据集。

数据集应包括n个观测值和p 个解释变量，其中每个解释变量都与一个因变量相关联。

如果存在高度相关的解释变量，可能会出现多重共线性问题。

PCR通过将解释变量进行主成分分析，来处理这个问题。

主成分分析（Principal Component Analysis，PCA）是一种降维技术，可以将原始数据转换为一组无关的主成分。

这些主成分是原始解释变量的线性组合，是按照解释变量方差降序排列的。

通过保留主成分的前k个，可以实现数据的降维。

选择k的方法包括手动选择、保留解释变量方差的一定比例或使用交叉验证等。

接下来，对于PCR，我们需要进行主成分回归。

具体步骤如下：步骤一：进行主成分分析对于p个解释变量，进行主成分分析得到k个主成分。

这里，k是一个小于等于p的数，用于控制降维的程度。

主成分分析的目标是找到能够最大程度解释解释变量方差的主成分。

步骤二：选择主成分个数k选择主成分个数k的方法有很多。

一种常用的方法是保留能够解释总方差的一定比例，例如95。

也可以使用交叉验证等其他方法。

步骤三：建立主成分回归模型利用保留的k个主成分，建立主成分回归模型。

在PCR中，主成分回归模型是一个线性回归模型，其中主成分是解释变量。

可通过普通最小二乘法估计回归系数。

步骤四：模型评估和选择通过交叉验证等方法对PCR模型进行评估，并选择最佳模型。

可以使用各种性能指标，例如均方误差、决定系数等。

PCR的优点是能够处理高维数据和共线性问题，并提高预测能力。

同时，PCR也允许我们了解每个主成分对因变量的贡献程度，帮助我们理解解释变量对模型的影响。

然而，PCR也存在一些限制。