数制转换

进制转换规则⼀、⼗进制与⼆进制之间的相互转换⼗进制——>⼆进制1. 整数部分和⼩数部分分别转换，2.⼗进制整数转换为⼆进制整数：除2，由下往上取余3.⼗进制⼩数转换为⼆进制⼩数：乘2，由上往下取整⼆进制——>⼗进制将⼆进制数的每⼀位数乘以它的权，然后相加，即可求得对应的⼗进制数值。

⼆、⼋进制与⼗进制、⼆进制之间的相互转换⼆进制——>⼋进制从⼩数点起，每三位⼆进制位分成⼀组（不⾜3位时，在⼩数点左边时左边补0，在⼩数点右边时右边补0），然后写出每⼀组的等值⼋进制数，顺序排列起来就得到所要求的的⼋进制数。

⼋进制——>⼆进制将每⼀位⼋进制数⽤三位⼆进制数表⽰，就可以直接将⼋进制数转换成⼆进制数。

⼋进制——>⼗进制将⼋进制数的每⼀位数乘以它的权，然后相加，即可求得对应的⼗进制数值。

⼗进制——>⼋进制1. 整数部分和⼩数部分分别转换，2.⼗进制整数转换为⼋进制整数：除8，由下往上取余3.⼗进制⼩数转换为⼋进制⼩数：乘8，由上往下取整三、⼗六进制与⼗进制、⼆进制之间的相互转换⼗六进制——>⼗进制将⼗六进制数的每⼀位数乘以它的权，然后相加，即可求得对应的⼗进制数值。

⼗进制——>⼗六进制1. 整数部分和⼩数部分分别转换，2.⼗进制整数转换为⼗六进制整数：除16，由下往上取余3.⼗进制⼩数转换为⼗六进制⼩数：乘16，由上往下取整⼗六进制——>⼆进制将每⼀位⼗六进制数⽤四位⼆进制数表⽰，就可以直接将⼗六进制数转换成⼆进制数。

⼆进制——>⼗六进制从⼩数点开始，每4位⼆进制数为⼀组（不⾜4位时，在⼩数点左边时左边补0，在⼩数点右边时右边补0），将每⼀组⽤相应的⼗六进制数符来表⽰，即可得到正确的⼗六进制数。

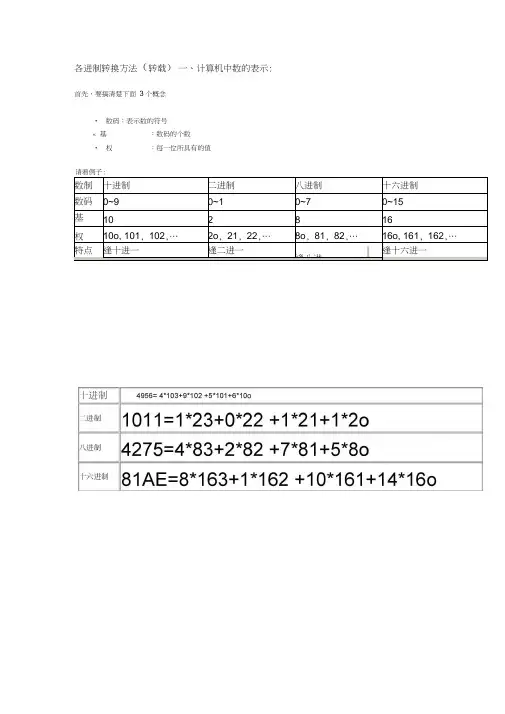
各进制转换方法（转载）一、计算机中数的表示: 首先，要搞清楚下面3个概念•数码：表示数的符号« 基：数码的个数•权：每一位所具有的值、各种进制的转换问题1. 二、八、十六进制转换成十进制2. 十进制转换成二、八、十六进制3. 二进制、八进制的互相转换4. 二进制、十六进制的互相转换1、二、八、十六进制转换成十进制方法：数码乘以相应权之和例(HloJ-l/25+lx24+l/23+0/22+ h2:+h20 -(59)10例(136)8=lx82+3x8l+6x8°=(94)10例(1F2^)1S=1X163+15X16S +2\16] + 10/16° = (7978)102、十进制转换成二、八、十六进制方法：连续除以基，直至商为0,从低到高记录余数例把十进制数159转换成八进制数 8| 198辽(159)IO =(237)8例把十进制数59转换成二进制数(59)IO =(111O11)22 余余余余余余8 159例把十进制数459转换成十六进制数u | 1| C| B(459)io=(1CB)ib '3、二进制、八进制的互相转换方法：*二进制转换成八进制：从右向左，每3位一组(不足3位左补0),转换成八进制*八进制转换成二进制：用3位二进制数代替每一位八进制数例(1101001)2=(001,101,001)2=(151)8例(246)8=(010,100,110)2=(10100110)24、二进制、十六进制的互相转换方法：二进制转换成十六进制：从右向左，每4位一组(不足4位左补0)，转换成十六进制*十六进制转换成二进制：用4位二进制数代替每一位十六进制数例(11010101111101)2=(0011,0101,0111,1101)2=(357D)16例(4B9E)16=(0100,1011,1001,1110)2=(100101110011110)2三、各种进制数的运算方法：逢满进具体计算与平时十进制的计算类似，以十六进制为例: 加法：05C3 + 3D2542 E83D25…05C3376205C3 X OOAB3F61 + 399E3D941。

各种进制转换
进制是数学中的一个重要概念，它指的是数的表示方式。

在计算机科学中，常用的进制有二进制、八进制和十六进制。

不同进制下的数在形式上有所差异，但其本质并没有变化。

二进制是计算机中最基础的进制，它只包含两个数字0和1。

二进制常用于表示计算机中的数据。

我们可以通过将十进制数不断地除以2，来将十进制数转换为二进制数。

例如，将十进制数13转换为二进制数，我们可以依次进行以下操作：
13 ÷ 2 = 6 余 1
6 ÷ 2 = 3 余 0
3 ÷ 2 = 1 余 1
1 ÷
2 = 0 余 1
将以上余数倒序排列，得到的二进制数为1101。

八进制和十六进制，分别包含8和16个数字。

它们常用于表示计算机中的颜色、地址和编码等数据。

八进制和十六进制数的转换同样可以通过不断地除以对应的进制数来实现。

例如，将十进制数100转换为八进制数，则可以依次进行以下操作：
100 ÷ 8 = 12 余 4
12 ÷ 8 = 1 余 4
1 ÷ 8 = 0 余 1
将以上余数倒序排列，得到的八进制数为144。

类似地，将十进制数100转换为十六进制数，可以依次进行以下
操作：
100 ÷ 16 = 6 余 4
6 ÷ 16 = 0 余 6
将以上余数倒序排列，得到的十六进制数为64。

总之，进制转换是计算机科学中的一项基本技能，它可以帮助我们更好地理解和处理计算机中的数据。

各种进制之间的转换方法进制转换是指将数字从一种进制表示转换为另一种进制表示。

常见的进制有二进制、八进制、十进制和十六进制。

下面将详细介绍各种进制之间的转换方法。

1.二进制转换为十进制：二进制数是由0和1组成的数字序列。

转换为十进制的方法是，将二进制数每一位上的数字乘以2的幂次方，然后将得到的结果相加。

例如：将二进制数1101转换为十进制，计算方法为：1*2^3+1*2^2+0*2^1+1*2^0=8+4+0+1=132.八进制转换为十进制：八进制数是由0到7之间的数字组成的数字序列。

转换为十进制的方法与二进制类似，只是要将八进制数每一位上的数字乘以8的幂次方，然后将得到的结果相加。

例如：将八进制数157转换为十进制，计算方法为：1*8^2+5*8^1+7*8^0=64+40+7=1113.十六进制转换为十进制：十六进制数是由0到9和A到F之间的数字和字母组成的数字序列，其中A表示十进制的10，B表示十进制的11，以此类推。

转换为十进制的方法是，将十六进制数每一位上的数字或字母转换为对应的十进制数，然后将得到的结果相加。

例如：将十六进制数1E8转换为十进制，计算方法为：1*16^2+14*16^1+8*16^0=256+224+8=4884.十进制转换为二进制：将十进制数转换为二进制的方法是，使用除2取余法。

即将十进制数连续除以2，将得到的余数从下往上排列，直到商为0为止。

例如：将十进制数43转换为二进制，计算方法为：43÷2=21余121÷2=10余110÷2=5余05÷2=2余12÷2=1余01÷2=0余15.十进制转换为八进制：将十进制数转换为八进制的方法是，使用除8取余法。

即将十进制数连续除以8，将得到的余数从下往上排列，直到商为0为止。

例如：将十进制数145转换为八进制，计算方法为：145÷8=18余118÷8=2余22÷8=0余2从下往上排列得到八进制数2216.十进制转换为十六进制：将十进制数转换为十六进制的方法是，使用除16取余法。

一、二进制转十进制由二进制数转换成十进制数的基本做法是，把二进制数首先写成加权系数展开式，然后按十进制加法规则求和。

这种做法称为按权相加法。

二、十进制转二进制十进制数转换为二进制数时，由于整数和小数的转换方法不同，所以先将十进制数的整数部分和小数部分分别转换后，再加以合并。

1. 十进制整数转换为二进制整数十进制整数转换为二进制整数采用除2取余，逆序排列法。

具体做法是：用2去除十进制整数，可以得到一个商和余数；再用2去除商，又会得到一个商和余数，如此进行，直到商为零时为止，然后把先得到的余数作为二进制数的低位有效位，后得到的余数作为二进制数的高位有效位，依次排列起来。

2．十进制小数转换为二进制小数十进制小数转换成二进制小数采用乘2取整，顺序排列法。

具体做法是：用2乘十进制小数，可以得到积，将积的整数部分取出，再用2乘余下的小数部分，又得到一个积，再将积的整数部分取出，如此进行，直到积中的小数部分为零，或者达到所要求的精度为止。

然后把取出的整数部分按顺序排列起来，先取的整数作为二进制小数的高位有效位，后取的整数作为低位有效位。

1．二进制与十进制的转换（1）二进制转十进制方法：按权展开求和例：（1011.01）2 ＝（1×23＋0×22＋1×21＋1×20＋0×2－1＋1×2－2）10＝（8＋0＋2＋1＋0＋0.25）10＝（11.25）10（2）十进制转二进制十进制整数转二进制数：除以2取余，逆序输出例：（89）10＝（1011001）22 892 44 12 22 02 11 02 5 12 2 12 1 00 1十进制小数转二进制数：乘以2取整，顺序输出例：(0．625)10= (0．101)20．625 X 21．25 X 20．5 X 21．02．八进制与二进制的转换例：将八进制的37.416转换成二进制数：37 ． 4 1 6011 111 ．100 001 110即：（37.416）8 ＝（11111.10000111）2例：将二进制的10110.0011 转换成八进制：0 1 0 1 1 0 . 0 0 1 1 0 02 6 . 1 4即：（10110.011）2 ＝（26.14）83．十六进制与二进制的转换例：将十六进制数5DF.9 转换成二十进制转二进制：用2辗转相除至结果为1将余数和最后的1从下向上倒序写就是结果例如：302转化成二进制302/2 = 151 余0151/2 = 75 余175/2 = 37 余137/2 = 18 余118/2 = 9 余09/2 = 4 余14/2 = 2 余02/2 = 1 余0故二进制为100101110二进制转十进制从最后一位开始算，依次列为第0、1、2...位第n位的数（0或1）乘以2的n次方得到的结果相加就是答案例如:01101011.转十进制:第0位:1乘2的0次方=11乘2的1次方=20乘2的2次方＝01乘2的3次方＝80乘2的4次方＝01乘2的5次方＝321乘2的6次方＝640乘2的7次方＝0然后：1＋2＋0＋8＋0＋32＋64＋0＝107．二进制01101011＝十进制107．。

二进制、八进制、十进制、十六进制之间转换一、十进制转换为其他进制方法：以二进制为例，除2取余法，即每次将整数部分除以2，余数为该位权上的数，而商继续除以2，余数又为上一个位权上的数，这个步骤一直持续下去，直到商为0为止，最后读数时候，从最后一个余数读起，一直到最前面的一个余数。

下面举例：例：将十进制的168转换为二进制步骤:第一步，将168除以2,商84,余数为0。

第二步，将商84除以2，商42余数为0。

第三步，将商42除以2，商21余数为0。

第四步，将商21除以2，商10余数为1。

第五步，将商10除以2，商5余数为0。

第六步，将商5除以2，商2余数为1。

第七步，将商2除以2，商1余数为0。

第八步，将商1除以2，商0余数为1。

最后，读数，因为最后一位是经过多次除以2才得到的，因此它是最高位，读数字从最后的余数向前读，即10101000将十进制转化为八进制与十六进制，原理相同，每次做除法时把除数变成8或16即可。

例：将十进制的5621转换为八进制步骤:第一步，将5621除以8,商702,余数为5。

第二步，将商702除以8，商87余数为6。

第三步，将商87除以8，商10余数为7。

第四步，将商10除以8，商1余数为2。

第五步，将商1除以8，商0余数为1。

最后，读数，因为最后一位是经过多次除以8才得到的，因此它是最高位，读数字从最后的余数向前读，即12765（2）二进制转换为十进制方法：从最后一位开始算，依次列为第0、1、2...位第n位的数（0或1）乘以2的n次方得到的结果相加就是答案。

例如：二进制1101011 转十进制：第0位（最后一位）:1乘2的0次方=1第1位（最后第二位）：1乘2的1次方=2第2位（最后第三位）：0乘2的2次方＝0第3位（最后第四位）：1乘2的3次方＝8第4位（最后第五位）：0乘2的4次方＝0第5位（最后第六位）：1乘2的5次方＝32第6位（最后第七位）：1乘2的6次方＝64最后：1＋2＋0＋8＋0＋32＋64＋0＝107．二进制1101011＝十进制107．二、二进制、八进制与十六进制的关系首先，我们需要了解一个数学关系，即2^3=8，2^4=16，而八进制和十六进制是用这关系衍生而来的，即用三位二进制表示一位八进制，用四位二进制表示一位十六进制数。

各种进制之间的转换稿子一嘿，亲爱的小伙伴们！今天咱们来聊聊各种进制之间的转换，这可有趣啦！你知道吗，咱们平常最常用的是十进制，就是从 0 到 9 这十个数字，满十就进一位。

比如说 19 再加 1 就变成 20 啦。

那二进制呢，就只有 0 和 1 两个数字。

电脑可喜欢二进制啦，像 1010 这样的。

把十进制转成二进制，咱们可以用除以 2 取余数的办法。

比如说 10 这个数，除以 2 商 5 余 0，5 再除以 2 商 2 余1，2 除以 2 商 1 余 0，1 除以 2 商 0 余 1，从下往上把余数排起来就是 1010 啦。

八进制呢，就是用到 0 到 7 这几个数字。

把十进制转成八进制，就除以 8 取余数。

十六进制就更酷啦，除了 0 到 9 还加上了 A 到 F 来表示 10 到 15 。

比如说 15 在十六进制里就是 F 。

进制转换其实不难，多练练就熟啦，是不是还挺好玩的？稿子二哈喽呀！今天咱们好好唠唠各种进制之间的转换。

先说说十进制，这可是咱们生活中最熟悉的啦，买东西、数数都靠它。

但世界可不止十进制这一种哦。

二进制，别看它就俩数字 0 和 1 ，作用老大了！电脑里的信息都是靠它传递的。

想把十进制数变成二进制，咱们就一直除以 2 ，然后把每次的余数记下来，倒着一拼就成啦。

八进制呢，每次要除以 8 。

比如说 20 除以 8 得 2 余 4 ，那八进制就是 24 。

还有十六进制，它更复杂点，不过也别怕。

数字不够用字母凑，A 代表 10 ，B 代表 11 ，一直到 F 代表 15 。

转换的时候也是除以16 取余数。

学会这些进制转换，感觉自己就像个数字小魔法师，能在不同的世界里自由穿梭。

怎么样，是不是很有意思？多试试，你也能玩转各种进制！加油哦，相信聪明的你肯定能轻松掌握！。

进制数的转换在计算机科学中，进制数是十分重要的概念。

进制数是指使用一定的进位规则，将数字表示为不同进制下的数。

常见的进制有二进制、八进制、十进制和十六进制。

在计算机中，二进制是最常用的进制，因为计算机内部的所有数据都是以二进制形式存储的。

因此，我们需要掌握进制数的转换方法，以便在编程和计算机科学中应用。

一、二进制转八进制和十六进制将二进制数转换为八进制或十六进制，需要先将二进制数转换为十进制数，然后再将十进制数转换为八进制或十六进制。

下面是一个将二进制数转换为八进制和十六进制的示例：1. 将二进制数10110101转换为八进制数。

首先，将二进制数转换为十进制数：101101012 = 1 × 27 + 0 × 26 + 1 × 25 + 1 × 24 + 0 ×23 + 1 × 22 + 0 × 21 + 1 × 20= 18110然后，将十进制数181除以8，得到商22和余数5。

将余数5作为八进制数的第一位。

将商22再次除以8，得到商2和余数6。

将余数6作为八进制数的第二位。

最后，将商2作为八进制数的第三位。

因此，二进制数10110101转换为八进制数265。

2. 将二进制数10110101转换为十六进制数。

首先，将二进制数转换为十进制数：101101012 = 1 × 27 + 0 × 26 + 1 × 25 + 1 × 24 + 0 ×23 + 1 × 22 + 0 × 21 + 1 × 20= 18110然后，将十进制数181除以16，得到商11和余数5。

将余数5作为十六进制数的第一位。

将商11再次除以16，得到商0和余数11。

将余数11转换为十六进制中的B，作为十六进制数的第二位。

因为商为0，所以最后的十六进制数为5B。

二、八进制和十六进制转二进制将八进制或十六进制数转换为二进制数，需要将每个八进制或十六进制位转换为对应的三个或四个二进制位。

进制转化公式
进制转化公式主要包括二进制转十进制、十进制转二进制、十进制转十六进制和十六进制转十进制四种。

1. 二进制转十进制公式：
将二进制数从左往右排列，分别与2的幂相乘，然后求和。

例如，二进制数1101转化为十进制数的计算公式为：
1 * 2^3 + 1 * 2^
2 + 0 * 2^1 + 1 * 2^0 = 13
2. 十进制转二进制公式：
将十进制数不断地除以2，并记录余数。

直到商为0为止，将记录的余数倒序排列即可。

例如，十进制数26转化为二进制数的计算公式为：
26 ÷ 2 = 商13，余0
13 ÷ 2 = 商6，余1
6 ÷ 2 = 商3，余0
3 ÷ 2 = 商1，余1
1 ÷
2 = 商0，余1
倒序排列余数为11010
3. 十进制转十六进制公式：
将十进制数不断地除以16，并记录余数。

直到商为0为止，将记录的余数倒序排列并转换成对应的字母即可。

例如，十进制数314转化为十六进制数的计算公式为：
314 ÷ 16 = 商19，余10（A）
19 ÷ 16 = 商1，余3
1 ÷ 16 = 商0，余1
倒序排列余数为13A
4. 十六进制转十进制公式：
将十六进制数从左往右排列，分别与16的幂相乘，然后求和。

例如，十六进制数1E转化为十进制数的计算公式为：
1 * 16^1 + 14 * 16^0 = 30
注意：以上都是简化说明，实际计算还需要考虑到进位和进位借位等情况。

二进制、八进制、十进制、十六进制互相转换方法1. 二进制转换为八进制：首先将二进制数按照每3位进行分组，不足3位的在左侧用0补齐。

然后将每组的二进制数转换为对应的八进制数，如下所示：二进制： 1011010分组： 001 011 010八进制： 1 3 2因此，二进制数1011010转换为八进制数为132。

2. 八进制转换为二进制：将八进制数的每一位数转换为对应的3位二进制数，不足3位的在左侧用0补齐，然后将这些二进制数拼接起来。

八进制： 327二进制： 011 010 111拼接： 011010111因此，八进制数327转换为二进制数为011010111。

3. 十进制转换为二进制：除以2，将商和余数记录下来，直到商为0。

然后将这些余数从最后一个开始依次排列即可。

十进制： 198除以2：商99 余数0商49 余数1商24 余数0商12 余数1商6 余数0商3 余数1商1 余数1商0 余数1结果： 11000110因此，十进制数198转换为二进制数为11000110。

4. 二进制转换为十进制：将二进制数的每一位与对应的位权相乘，然后将乘积相加即可。

二进制： 11000110位权： 2^7 2^6 2^5 2^4 2^3 2^2 2^1 2^0结果： 128 64 32 16 8 4 2 0计算： 128*1 + 64*1 + 32*0 + 16*0 + 8*0 + 4*1 + 2*1 + 0*0 因此，二进制数11000110转换为十进制数为198。

5. 十进制转换为十六进制：除以16，将商和余数记录下来，直到商为0。

然后将这些余数从最后一个开始依次排列即可，注意10-15分别用字母A-F表示。

十进制： 256除以16：商16 余数0商1 余数0商0 余数1结果： 100因此，十进制数256转换为十六进制数为100。

6. 十六进制转换为十进制：将十六进制数的每一位与对应的位权相乘，然后将乘积相加即可，注意10-15分别用字母A-F表示。

进制转换计算方法【简单】
1.其他进制转成十进制
（1）整数
以二进制为例：100100
转成十进制从左到右乘以2的n-1次幂：1*2^5+0*2^4+0*2^3+1*2^2+0*2^1+0*2^0=36 （2）小数
以二进制为例：0.10010
转成十进制从左到右乘以2的n-1次幂：0*2^0+1*2^-1+0*2^-2+0*2^-3+1*2^-4+0*2^-5=0+0.5+0+0+0.0625+0=0.5625
其他进制数据转化方式等同
2.十进制转成其他进制
（1）整数
以二进制为例：36转成二进制
36/2=18 0
18/2=9 0
9/2=4 (1)
4/2=2 0
2/2=1 0
1/2=0 (1)
直到商为0为止，余数从右到左组合到一起即为2进制数值100100
（2）小数
以二进制为例：0.36转成二进制
0.36*2=0.72 0
0.72*2=1.44 (1)
0.44*2=0.88 0
0.88*2=1.76 (1)
0.76*2=1.52 (1)
0.52*2=1.04 (1)
直到十分位为0为止，整数位从右到左组合到一起即为2进制数值111010
其他进制数据转化方式等同。

3.其他进制之间转换要以十进制作为纽带进行转换
比如八进制转成二进制：要先把八进制转成十进制，再转成二进制。

二进制八进制十进制十六进制四种算法之间的互相转换1.二进制转十进制：二进制数是基于2的数制系统，只包含0和1两个数字。

转换二进制数到十进制数非常简单，只需要将二进制数中的每个数字乘以2的幂次方，然后将结果相加即可。

例如，二进制数"1010"转换为十进制数的计算方法如下：1*2^3+0*2^2+1*2^1+0*2^0=8+0+2+0=102.八进制转十进制：八进制数是基于8的数制系统，只包含0到7的数字。

转换八进制数到十进制数也非常简单，只需要将八进制数中的每个数字乘以8的幂次方，然后将结果相加即可。

例如，八进制数"753"转换为十进制数的计算方法如下：7*8^2+5*8^1+3*8^0=7*64+5*8+3=448+40+3=4913.十六进制转十进制：十六进制数是基于16的数制系统，包含0到9的数字和A到F的字母。

转换十六进制数到十进制数也非常简单，只需要将每个十六进制数字乘以16的幂次方，然后将结果相加即可。

其中字母A到F分别表示10到15、例如，十六进制数"3AF"转换为十进制数的计算方法如下：3*16^2+10*16^1+15*16^0=3*256+10*16+15=768+160+15=9434.十进制转二进制：十进制数是我们日常生活中最常用的数制系统，包含数字0到9、转换十进制数到二进制数可以使用除2取余法。

具体步骤是：将十进制数除以2，直到商为0，然后将每次的余数倒序排列起来作为二进制数的结果。

例如，将十进制数10转换为二进制数的步骤如下：10/2=5余05/2=2余12/2=1余01/2=0余1倒序排列余数得到二进制数"1010"。

5.十进制转八进制：将十进制数转换为八进制数也可以使用除8取余法。

具体步骤与转换为二进制数相似，只需要将除数改为8即可。

例如，将十进制数25转换为八进制数的步骤如下：25/8=3余13/8=0余3倒序排列余数得到八进制数"31"。

各种进制之间的转换方法
首先，我们来讨论二进制和十进制之间的转换方法。

二进制是计算机中最常用的进制，而十进制则是我们日常生活中最常见的进制。

在二进制和十进制之间进行转换时，最简单的方法是将二进制数按权展开，然后相加即可得到其对应的十进制数。

例如，二进制数1011可以按权展开为12^3 + 02^2 + 12^1 + 12^0，计算后得到对应的十进制数为11。

接下来是八进制和十进制之间的转换方法。

八进制是以8为基数的进制，而十进制是以10为基数的进制。

在八进制和十进制之间进行转换时，我们可以将八进制数按权展开，然后相加得到其对应的十进制数，或者将十进制数除以8并取余数得到其对应的八进制数。

然后是十六进制和十进制之间的转换方法。

十六进制是以16为基数的进制，常用于表示颜色、内存地址等信息。

在十六进制和十进制之间进行转换时，我们可以将十六进制数按权展开，然后相加得到其对应的十进制数，或者将十进制数除以16并取余数得到其对应的十六进制数。

除了以上介绍的进制之间的转换方法，我们还可以通过进制之
间的转换来进行加减乘除运算。

例如，在二进制中进行加法运算时，我们可以按位相加，并注意进位的处理；在十六进制中进行乘法运
算时，我们可以将十六进制数转换为十进制数后进行乘法运算，再
将结果转换回十六进制数。

总之，掌握各种进制之间的转换方法对于理解计算机原理和进
行编程是非常重要的。

通过本文的介绍，希望读者能够更好地理解
和运用各种进制之间的转换方法，从而提高自己在计算机科学和数
学领域的能力。

进制间的相互转换1.十进制（1）、十进制转二进制十进制整数转换为二进制整数采用"除2取余，逆序排列"法。

例如：（2）、十进制转八进制和转为二进制一样，将十进制数除以八，按顺序记录每次得到的余数，直到商为0，然后将得到的各个余数从最后得到的那个开始向右排起就是一个八进制数了例如：（3）、十进制转十六进制跟上面差不多，就是变成了除以16例如：2.二进制（1）、二进制转十进制从二进制的右边第一个数开始，每一个乘以2的n次方，n从0开始，每次递增1。

然后得出来的每个数相加即是十进制数。

（2）、二进制转八进制取三合一法，即从二进制的小数点为分界点，向左(向右）每三位取成一位，接着将这三位二进制按权相加，得到的数就是一位八位二进制数，然后，按顺序进行排列，小数点的位置不变，得到的数字就是我们所求的八进制数。

如果向左（向右)取三位后，取到最高（最低)位时候，如果无法凑足三位，可以在小数点最左边（最右边)，即整数的最高位(最低位）添0，凑足三位。

例:1、将二进制数101110.101转换为八进制得到结果:将101110.101转换为八进制为56.52、将二进制数1101.1转换为八进制得到结果:将1101.1转换为八进制为15.4简易背过，也可以自己找规律。

（3）、二进制转十六进制二进制转换成十六进制的方法是，取四合一法，即从二进制的小数点为分界点，向左（或向右）每四位取成一位3.八进制(1)，八进制转二进制八进制转二进制，另一方面，方法是三分之一，即将一个八进制数除以三个二进制数，将三个二进制数加权相加，最后得到二进制，小数点还是可以的。

可以参考上表（2）、八进制转十进制跟二进制转换为十进制差不多（3）、八进制转化为十六进制八进制转换bai成十六进制算法通常有两种方法：1、先将八进制转换成二进制，再将二进制转换成十六进制2、先将八进制转换成十进制，再将十进制转换成十六进制4.十六进制（1）、十六进制转换为二进制将16进制转为二进制，反过来啦，方法就是一分四，即一个十六进制数分成四个二进制数，用四位二进制按权相加，最后得到二进制，小数点依旧就可以啦（2）、十六进制转换为十进制和上面的二进制转十进制和八进制转十进制差不多（3）、十六进制转八进制可以先转换成十进制，再转换成十六进制。

各种进制的相互转换在计算机科学中，常用的进制有二进制、八进制、十进制和十六进制。

进制相互转换的方法如下：1、二进制转八进制二进制数每三位一组，从小数点开始向左或向右加0补齐，再将每组转换为相应的八进制数即可。

例如：二进制数111101.1101，将小数点左边的111101和右边的1101分别转换为八进制数，即得到：175.54。

2、八进制转二进制将每个八进制数转换为相应的三位二进制数，再将结果拼接在一起即可。

例如：八进制数345.67，将3、4、5、6、7分别转换为三位二进制数，即011、100、101、110、111，连接起来即得到：011100101110.110。

3、二进制转十六进制二进制数每四位一组，从小数点开始向左或向右加0补齐，再将每组转换为相应的十六进制数即可。

例如：二进制数101110.0111，将小数点左边的101110和右边的0111分别转换为十六进制数，即得到：5E.7。

4、十六进制转二进制将每个十六进制数转换为相应的四位二进制数，再将结果拼接在一起即可。

例如：十六进制数3C.5D，将3、C、5、D分别转换为四位二进制数，即0011、1100、0101、1101，连接起来即得到：0011110001011101。

5、十进制转二进制将十进制数不断除以2，得到的余数即为二进制数的每一位，将余数从低位到高位排列即可。

例如：十进制数153，将其除以2得到商76、余数1，再将76除以2得到商38、余数0，依次计算下去得到二进制数10011001。

6、二进制转十进制将每一位上的数值乘上2的n次方（从右到左，n从0开始递增），再将结果相加即可。

例如：二进制数1011001，将其中每一位上的数值乘上2的n次方，然后相加，即得到：1×2^6+0×2^5+1×2^4+1×2^3+0×2^2+0×2^1+1×2^0=89。

以上是进制相互转换的一些基本方法，可以方便地将不同进制之间的数据互相转换。

进制转换原理进制转换是指将一个数值从一种进制表示方式转换为另一种进制表示方式的过程。

常见的进制包括十进制、二进制、八进制及十六进制。

在进行进制转换时，需要了解每种进制的权重计算方式。

以十进制为例，权重是按数字所在位数依次递增的，从右到左依次为1、10、100、1000，以此类推。

而在二进制中，权重是按2的幂次递增的，从右到左依次为1、2、4、8，以此类推。

进制转换的过程是通过对原数值依次进行除法和取余操作，将数值从原进制转换为目标进制。

具体步骤如下：1. 将原数值除以目标进制的基数，并记录商和余数。

2. 将记录的余数作为目标进制下对应位的数值。

3. 将商作为新的被除数，重复步骤1和步骤2，直至商为0为止。

4. 将所有记录的余数按相反顺序排列，得到目标进制下的数值。

举例来说，将十进制数值18转换为二进制数值的过程如下：1. 将18除以2，商为9，余数为0。

2. 用余数0作为二进制的个位数。

3. 将9除以2，商为4，余数为1。

4. 用余数1作为二进制的十位数。

5. 将4除以2，商为2，余数为0。

6. 用余数0作为二进制的百位数。

7. 将2除以2，商为1，余数为0。

8. 用余数0作为二进制的千位数。

9. 将1除以2，商为0，余数为1。

10. 用余数1作为二进制的万位数。

11. 将记录的余数按从高位到低位的顺序排列，得到二进制数值11010。

通过以上步骤，将十进制数值18成功转换为二进制数值11010。

同样的方法也适用于将其他进制转换为十进制，以及不同进制之间的相互转换。

在高速发展的现代社会，计算机浩浩荡荡地成为了人们生活中不可缺少的一部分，帮助人们解决通信，联络，互动等各方面的问题。

今天我就给大家讲讲与计算机甚至日常生活有密切相关的“进制转换”问题。

我们以（25.625）（十）为例讲解一下进制之间的转化问题。

1. 十-----> 二给你一个十进制，比如：6，如果将它转换成二进制数呢？10进制数转换成二进制数，这是一个连续除2的过程：把要转换的数，除以2，得到商和余数，将商继续除以2，直到商为0。

最后将所有余数倒序排列，得到数就是转换结果。

听起来有些糊涂？我们结合例子来说明。

比如要转换6为二进制数。

“把要转换的数，除以2，得到商和余数”。

那么：十转二示意图要转换的数是6， 6 ÷ 2，得到商是3，余数是0。

“将商继续除以2,直到商为0……”现在商是3，还不是0，所以继续除以2。

那就： 3 ÷ 2, 得到商是1,余数是1。

“将商继续除以2，直到商为0……”现在商是1，还不是0，所以继续除以2。

那就： 1 ÷ 2, 得到商是0，余数是1“将商继续除以2，直到商为0……最后将所有余数倒序排列”好极！现在商已经是0。

我们三次计算依次得到余数分别是：0、1、1，将所有余数倒序排列，那就是：110了！6转换成二进制，结果是110。

把上面的一段改成用表格来表示，则为：被除数计算过程商余数6 6/2 3 03 3/2 1 11 1/2 0 1（在计算机中，÷用 / 来表示）2. 二----> 十二进制数转换为十进制数二进制数第0位的权值是2的0次方，第1位的权值是2的1次方……所以，设有一个二进制数：0110 0100，转换为10进制为：下面是竖式：0110 0100 换算成十进制" ^ " 为次方第0位 0 * 2^0 = 0第1位 0 * 2^1 = 0第2位 1 * 2^2 = 4第3位 0 * 2^3 = 0第4位 0 * 2^4 = 0第5位 1 * 2^5 = 32第6位 1 * 2^6 = 64第7位 0 * 2^7 = 0 ＋---------------------------100用横式计算为：0 * 2 ^ 0 + 0 * 2 ^ 1 + 1 * 2 ^ 2 + 0 * 2 ^ 3 + 0 * 2 ^ 4 + 1 * 2 ^ 5 + 1 * 2 ^ 6 + 0 * 2 ^ 7 = 1000乘以多少都是0，所以我们也可以直接跳过值为0的位：1 *2 ^ 2 + 1 * 2 ^ 5 + 1 * 2 ^ 6 = 1003. 十----> 八10进制数转换成8进制的方法，和转换为2进制的方法类似，唯一变化：除数由2变成8。

各种进制转换方法进制转换是计算机科学中非常重要的概念，涉及到各种数字系统之间的转换。

常见的进制包括十进制、二进制、八进制和十六进制。

下面将详细介绍各种进制之间的转换方法。

1.十进制转二进制：十进制转换为二进制的方法是对整数部分进行不断除2取余操作，直到商为0为止。

然后将余数按顺序排列，最后得到的余数就是二进制数。

例如，将十进制数23转换为二进制数，步骤如下：23÷2=11余111÷2=5余15÷2=2余12÷2=1余01÷2=0余12.二进制转十进制：1*2^4+0*2^3+1*2^2+1*2^1+1*2^0=16+0+4+2+1=233.十进制转八进制：十进制转换为八进制的方法是对整数部分进行不断除8取余操作，直到商为0为止。

然后将余数按顺序排列，最后得到的余数就是八进制数。

例如，将十进制数23转换为八进制数，步骤如下：23÷8=2余72÷8=0余2将余数倒序排列，得到八进制数274.八进制转十进制：八进制转换为十进制的方法是将八进制数每一位与其对应的权值相乘，然后将乘积相加。

例如，将八进制数27转换为十进制数，步骤如下：2*8^1+7*8^0=16+7=235.十进制转十六进制：十进制转换为十六进制的方法是对整数部分进行不断除16取余操作，直到商为0为止。

然后将余数按顺序排列，最后得到的余数就是十六进制数。

需要注意的是，余数大于9时，要用字母A、B、C、D、E、F表示10、11、12、13、14、15、例如，将十进制数23转换为十六进制数，步骤如下：23÷16=1余71÷16=0余1将余数倒序排列，其中余数7表示为十六进制字母7，得到十六进制数176.十六进制转十进制：十六进制转换为十进制的方法是将十六进制数每一位与其对应的权值相乘，然后将乘积相加。

其中乘积中的十六进制字母要用其对应的十进制数值替换。

例如，将十六进制数17转换为十进制数，步骤如下：1*16^1+7*16^0=16+7=23以上是常见的进制转换方法。

二进制、八进制、十进制、十六进制之间转换一、十进制与二进制之间的转换（1）十进制转换为二进制，分为整数部分和小数部分①整数部分方法：除2取余法，即每次将整数部分除以2，余数为该位权上的数，而商继续除以2，余数又为上一个位权上的数，这个步骤一直持续下去，直到商为0为止，最后读数时候，从最后一个余数读起，一直到最前面的一个余数。

下面举例：例：将十进制的168转换为二进制得出结果将十进制的168转换为二进制，（10101000）2分析:第一步，将168除以2,商84,余数为0。

第二步，将商84除以2，商42余数为0。

第三步，将商42除以2，商21余数为0。

第四步，将商21除以2，商10余数为1。

第五步，将商10除以2，商5余数为0。

第六步，将商5除以2，商2余数为1。

第七步，将商2除以2，商1余数为0。

第八步，将商1除以2，商0余数为1。

第九步，读数，因为最后一位是经过多次除以2才得到的，因此它是最高位，读数字从最后的余数向前读，即10101000（2）小数部分方法：乘2取整法，即将小数部分乘以2，然后取整数部分，剩下的小数部分继续乘以2，然后取整数部分，剩下的小数部分又乘以2，一直取到小数部分为零为止。

如果永远不能为零，就同十进制数的四舍五入一样，按照要求保留多少位小数时，就根据后面一位是0还是1，取舍，如果是零，舍掉，如果是1，向入一位。

换句话说就是0舍1入。

读数要从前面的整数读到后面的整数，下面举例：例1：将0.125换算为二进制得出结果：将0.125换算为二进制（0.001）2分析：第一步，将0.125乘以2，得0.25,则整数部分为0,小数部分为0.25;第二步, 将小数部分0.25乘以2,得0.5,则整数部分为0,小数部分为0.5;第三步, 将小数部分0.5乘以2,得1.0,则整数部分为1,小数部分为0.0;第四步,读数,从第一位读起,读到最后一位,即为0.001。

例2,将0.45转换为二进制（保留到小数点第四位）大家从上面步骤可以看出，当第五次做乘法时候，得到的结果是0.4，那么小数部分继续乘以2，得0.8，0.8又乘以2的，到1.6这样一直乘下去，最后不可能得到小数部分为零，因此，这个时候只好学习十进制的方法进行四舍五入了，但是二进制只有0和1两个，于是就出现0舍1入。