当前位置：文档之家 › 数制及其转换

数制及其转换

  • 格式：ppt
  • 大小：240.50 KB
  • 文档页数：38

下载文档原格式

  / 38

合集下载

常用数制及其相互转换

常用数制及其相互转换

一、常用数制及其相互转换在我们的日常生活中计数采用了多种记数制，比如：十进制，六十进制（六十秒为一分，六十分为一小时，即基数为60，运算规则是逢六十进一），……。

在计算机中常用到十进制数、二进制数、八进制数、十六进制数等，下面就这几种在计算机中常用的数制来介绍一下。

1．十进制数我们平时数数采用的是十进制数，这种数据是由十个不同的数字0、1、2、3、4、5、6、7、8、9任意组合构成，其特点是逢十进一。

任何一个十进制数均可拆分成由各位数字与其对应的权的乘积的总和。

例如：???这里的10为基数，各位数对应的权是以10为基数的整数次幂。

为了和其它的数制区别开来，我们在十进制数的外面加括号，且在其右下方加注10。

2．二进制数在计算机中，由于其物理特性（只有两种状态：有电、无电）的原因，所以在计算机的物理设备中获取、存储、传递、加工信息时只能采用二进制数。

二进制数是由两个数字0、1任意组合构成的，其特点是逢二进一。

例如：1001，这里不读一千零一，而是读作：一零零一或幺零零幺。

为了与其它的数制的数区别开来，我们在二进制数的外面加括号，且在其右下方加注2，或者在其后标B。

任何一个二进制数亦可拆分成由各位数字与其对应的权的乘积的总和。

其整数部分的权由低向高依次是：1、2、4、8、16、32、64、128、……，其小数部分的权由高向低依次是：0.5、0.25、0.125、0.0625、……。

二进制数也有其运算规则：加法：0+0=0????0+1=1???1+0=1????1+1=10乘法：0×0=0????0×1=0????1×0=0????1×1=1二进制数与十进制数如何转换：（1）二进制数—→十进制数对于较小的二进制数：对于较大的二进制数：方法1：各位上的数乘权求和??例如：（101101）2=1×25+0×24+1×23+1×22+0×21+1×20=45（1100.1101）2=1×23+1×22+0×21+0×20+1×2-1+1×2-2+0×2-3+1×2-4=12.8125方法2：任何一个二进制数可转化成若干个100…0?的数相加的总和??例如：（101101）2=（100000）2+（1000）2+（100）2+（1）2而这种100…00形式的二进制数与十进制数有如下关联：1后有n个0，则这个二进数所对应的十进制数为2n。

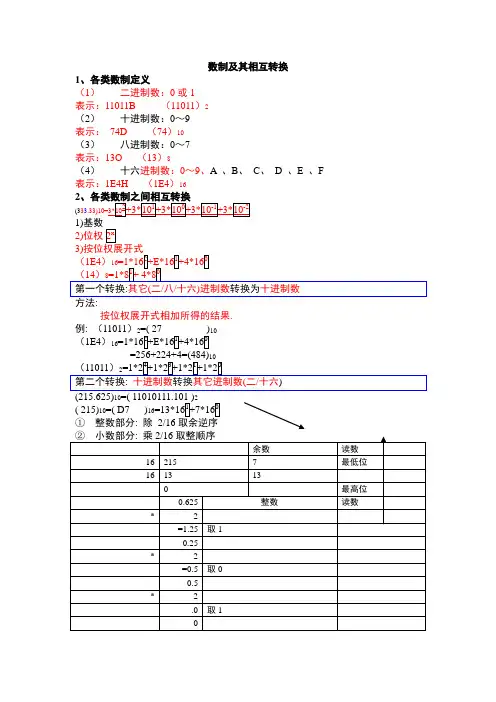
数制及其转换

数制及其转换

数制及其相互转换1、各类数制定义（1）二进制数：0或1表示：11011B （11011）2（2）十进制数：0～9表示：74D （74）10（3）八进制数：0～7表示：13O （13）8（4）十六进制数：0～9、A 、B、C、 D 、E 、F 表示：1E4H （1E4）162(3331)基数2)位权按位权展开式相加所得的结果.例: （11011）2（1E4）16102( 215)10=( D7 )16①整数部分: 除2/16方法:1位对3位0+0=0 0+1=1 1+0=1 1+1=10方法:3位对1位（以小数点为中心，不足3位左右对应补0）例如: ( 00 1 101 110 111. 110)2方法:4位对1位（类似二进制转换八进制，以小数点为中心，不足4位左右对应补0）例如: ( 00 11 0111 0111. 1100)2= (377. C)16数据单位1、位（bit）:0或12、字节（Byte）：1B= 8b4、字（W ord）字符编码1、ASCII码A）8 B）A C）a D）Z大写字母A 的ASCII码为（65）10（2）国标码例如：“啊”字的国标码为3021H求值：“啊”区位码为1601D，求“啊”的国标码①将区码、位码分别转换为十六进制16 1616 1 00 116D=10H01D=01H②将区码和位码十位进制数合在一起写 1001H③区位码H+2020H=国标码1001H+2020H=3021H（3）机内码机内码=国标码+8080H（4）汉字输入码（5）汉字的字形码16*16=256b/1B =8b/256/8占用32个字节24*24 32*32。

数的转换与转化

数的转换与转化

数的转换与转化数学是一门广泛应用于日常生活和各个学科领域的学科。

在实际应用中，我们常常需要进行数的转换和转化。

本文将探讨一些常见的数的转换和转化方法，并介绍一些数的转换和转化在实际生活中的应用。

一、数制的转换数制是用来表示数的一种方法。

常见的数制有十进制、二进制、八进制和十六进制等。

在不同的数制中，数的表示方式和基数不同，因此需要进行数制的转换。

1. 十进制转二进制十进制转二进制是将十进制数转换为二进制数的过程。

其方法是将十进制数不断除以2，并将余数倒排组成二进制数。

例如，将十进制数13转换为二进制数的过程如下：13÷2=6余16÷2=3余03÷2=1余11÷2=0余1将上述余数倒排，得到二进制数1101，即为十进制数13的二进制表示。

2. 二进制转十进制二进制转十进制是将二进制数转换为十进制数的过程。

其方法是将二进制数从最低位开始，逐位乘以2的幂，再求和。

例如，将二进制数1011转换为十进制数的过程如下：1×2^3 + 0×2^2 + 1×2^1 + 1×2^0 = 8 + 0 + 2 + 1 = 11将上述计算得到的和就是二进制数1011的十进制表示。

二、单位的转换单位的转换是将一种物理量表示方式转换为另一种物理量表示方式的过程。

在日常生活中，我们经常需要进行单位的转换，以满足不同情境下的需求。

1. 长度单位的转换长度单位常见的转换关系有米（m）、厘米（cm）和英寸（inch）。

其转换关系如下：1 m = 100 cm1 inch ≈ 2.54 cm例如，将10英寸转换为厘米的过程如下：10 inch × 2.54 cm/inch = 25.4 cm2. 温度单位的转换温度单位常见的转换关系有摄氏度（℃）和华氏度（℉）。

其转换关系如下：℉ = ℃ × 9/5 + 32℃ = (℉ - 32) × 5/9例如，将华氏度转换为摄氏度的过程如下：℉ = 100 ℃ × 9/5 + 32 = 212 ℉三、数的转化数的转化是指将某种数值转换为另一种数值的过程。

数制及其转换

数制及其转换

（9）1000 ∧ 1101 = （10）1111 ∨ 1011=
二、数制的转换 在数制的转换中，通常在数值后面加字母D、B、O、 H分别表示该数是10、2、8、16进制数，D、B、O、H 的含义分别是Decimal、Binary、Octal、Hexadecimal。 1、p进制转 进制 、 进制转 进制转10进制 ( kn kn–1…k1 k0 . k–1…k–m ) p= kn×p n + kn–1×p n–1 +… + k1×p + k0 + k–1×p –1 +…+ k–m×p –m 其中0≤k i < p，i = – m～n。p叫做p进制数的基数 基数， 基数 k i叫做该p进制数的第i位，p i叫做第i位的权。 位 权
例如: 12345=1*104+2*103+3*102+4*101+5*100
权
基数为10 也有用下标来表示进制
(10)10 (10)2 (10)8 (10)16
也可以用字母来表示 10D 10B 10O 10H
例如：101001.101 B = 2 5 + 2 3 + 1 + 2 –1 + 2 –3 = 32 + 8 + 1 + 0.5 + 0.125 = 41.625 D ABC.D H = A×16 2 + B×16 + C + D×16 –1 = 2560 + 176 + 12 + 13×0.0625 = 2748.8125 D
除法运算法则： 除法运算法则
例：求（1101. 1）2 ÷（110）2 ） ）
10.01） ＝ （？ ）2

大学计算机基础实验数制及其转换

大学计算机基础实验数制及其转换

§ 数制及其转换由于计算机采用二进制，而人们熟悉的是十进制，所以我们从分析数制入手，从而进一步了解、掌握计算机中所采用的各种数据的表示方法。

一．数制由十进制记数法抽象推理，可得到任意的R进制的表示规律：（1）R进制（基数R为大于1的任意正整数）：数码个数R个，分别为1、2、…R-1；（2）一个数据中相邻两数码的左边一个单位是右边一个单位的R 倍；（3）每个数位计满R 向高位进位（逢R 进位）；（4）R 进制表示的一个数的实际值为每一个位上的实际值的总和：其中R 为基数，i为位序号，Di 代表第i位上的一个数据符，可以是0到R-1符号中的任意一个，Ri 代表第i 位的位权，-K 和m-1分别是该数的最低位和在高位的位序号（N=k+m）。

（5）按权展开：二．计算机中常用的几种数制1．二进制（Binary） R=2，数符为0，1；逢二进一；二进制数的主要特点有：（1）实现简单：每个数位可用任意具有两个不同稳定状态的器件来表示。

如晶体管的导通与截止、电压的高与低、灯的亮与灭等均可存储、传送“0”和“1”。

（2）二进制的算术运算法则简单加法： 0+0=00+1=1+0=1 1+1=10 乘法： 0*0=0*1=1*0=0 1*1=1 例： 10101+111=100011101-110=111 1011*101=110111 101101÷110=111（余11）（3）可利用逻辑代数对二进制数进行逻辑运算逻辑与（AND）：0∧0=0∧1=1∧0=0 1∧1=1 逻辑或（OR）：0∨0=0 0∨1=1∨0=1∨1=1 逻辑非（NOT）：逻辑异或（XOR）：0⊕0=1⊕1=0 1⊕0=0⊕1=12．八进制（Octal）由于二进制数据的基R较小，所以二进制数据的书写和阅读不方便，为此，在小型机中引入了八进制。

八进制的基R=8=23，有数码0、1、2、3、4、5、6、7，并且每个数码正好对应三位二进制数，所以八进制能很好地反映二进制。

数制及其转换

数制及其转换

例：求（1101. 1）2 ÷（110）2
＝ （？10.01）2
10 .01
110 1101 .10
110 1 10 1 10 0
练习： （11111.01）2 × （11110.1）2 ＝
1 1 1 1 1. 0 1
×
1 1 1 1 0 .1
11111 0 1 1111101 1111101 1111101 1111101
例1 将12.3转换为二进制。 解：∵2×0.3 = 0.6 + 0 高
2×0.6 = 0.2 + 1 2×0.2 = 0.4 + 0 2×0.4 = 0.8 + 0 2×0.8 = 0.6 + 1 低 …………………… ∴ 0.3 0.01001 B , 12.3 1100.01001 B 。
＝ （？1100101.11）2
101 1011
＋） 1
1010.1
`
1
`
0
0
1`
0
1
.1
1 1
减法运算法则： 0－0＝0 1 －0 ＝1
例：求（10110.01）2 － （1100.10）2
＝ （？1001.11）2
1` 0 1 1` 0` . 0 1
－）
1100.1 0
1 0 0 1 .1 1
2i
，k
i
=
0或1，
i0
则( x ) 10 = ( kn kn–1…k1 k0 )2。
例如：23 D = 2 4 + 2 2 + 2 + 1 = 10111 B，
257 = 2 8 + 1 = 100000001 B。
注：上述结果也可由常用数制对照表中的2—10进

数制及其转换

数制及其转换
进位计数制
（1）进位计数制的特点
①表示数值大小的数码与它在数中所处的位置有关。
以十进制数132.54为例。
数码1处于百位，表示1×102=100，位权为102；
数码3处于十位，表示3×101=30，位权为101；
数码2处于个位，表示2×100=2，位权为100；
数码5处于十分位，表示5×10-1=0.5，位权为10-1；
——十进制数转换成二进制数
将十进制数转换成二进制数时，先将十进制数分成整数部分和小数部分，然后再利用各自的转换法则进行转换，最后在保持小数点位置不变的前提下将两部分结果写在一起。
整数部分：“除2取余法”
将十进制数除以2，记下余数，将商再除以2，记下余数，……直到商数为0，将所得余数反序排列，即得该数的二进制表示。
简便算法：将十进制数分解成若干个2的整数次幂之和，则2的整次幂所在位为1，其余位为0。
[207]10=128+64+8+4+2+1=27+26+23+22+21+20=[11001111]2
不同进制数之间的转换
——十进制数转换成八进制数或十六进制数
将十进制数转换成八进制或十六进制，方法与将十进制数转换成二进制数相同，只是整数部分的“除2取余法”变成了“除8取余法”或“除16取余法”，小数部分的“乘2取整法”变成了“乘8取整法”或“乘16取整法”。
0+0=0 0+1=1+0=1 1+1=10
不同进位计数制的特点
计算机中常用的数制有：十进制、二进制、八进制、十六进制。
①十进制：基数有0、1、2、3、4、5、6、7、8、9，进位方式是逢十进一，位权表示为100、101、102、103……，即权值是10的幂。任一个数都可按权展开。

数制及其转换

常用数制及其相互转换1．十进制数有十个不同数字0—9，并且“逢十进一”。

对于任意一个十进制数，都可以表示成按权展开的多项式。

如：1804=1╳103+8╳102+0╳101+4╳10048.25=4╳101+8╳100+2╳10-1+5╳10-2十进制中，个、十、百、千，┄┄各位的权，分别为100、101、102、103，┄┄。

10被称为基数。

2．二进制数有二个不同数字：0和1，并且“逢二进一”。

基数是2，各数位的权是基数的整数次幂。

整数部分各数位的权从最低位开始依次是20、21、22、23、24、┄┄，小数部分各数位的权从最高位开始依次是2-1、2-2、2-3、┄┄。

二进制数的表示：如（1101）2，将二进制数用小括号括起来，右下角加个2。

问：二进制数的按权展开形式如何表示？（1101）2=1╳23+1╳22+0╳21+1╳20二进制数运算规则：0+0=0 0+1=1 1+0=1 1+1=100╳0=0 0╳1=0 1╳0=0 1╳1=13、二进制数与十进制数的相互转换（1）二进制数转换成十进制数（按权展开求和）。

例1：把（1101.01）2转换成十进制数（1011.01）2＝（1×23＋0×22＋1×21＋1×20＋0×2－1＋1×2－2）10＝（8＋0＋2＋1＋0＋0.25）10＝（11.25）10二进制数转十进制数，是将二进制数按权展开求和。

（2）十进制数转换成二进制数（除以2反序取余）。

例2：把（89）10转换成二进制数（89）10＝（1011001）22 89 余数2 44 (1)2 22 02 11 02 5 (1)2 2 (1)2 1 00 (1)十进制数转二进制数，是将十进制数除以2，除完为止，然后反序取余数。

即最先得到的余数作为最低位。

4、八进制数基数为8，有八个数字0—7，运算规则是“逢八进一”。

（1）十进制数转八进制数：除以8反序取余例：（215）10=（？）88 215 余数8 26 (7)8 3 (2)0 (3)所以（215）10=（327）8（2）八进制数转十进制数：按权展开求和例：（327）8=（？）10（327）8=3╳82+2╳81+7╳80=（215）10（3）八进制数转二进制数方法一：将八进制数转十进制数，再将十进制数转二进制数。

数制及其转换


十六进制数：1位化4位
二进制转化成八(十六)进制
整数部分：从右向左按3(4)位进行分组 小数部分：从左向右按3(4)位进行分组, 不足补零
二进制、八进制、十六进制数间的关系
23=8 4 2 1
八 进制 对应 二进制 十六 进制
24=16
对应 二进制 十六 进制
8421对应 二进制0 1 2 3 4 5
使计算机的硬件结构大大简化。 （3）二进制的“1”和“0” 与逻辑命题 两个值“真”和“假”相对应，为 计算机实现逻辑运算提供了便利。
问题：
引入八进制和十六进制
用二进制表示有缺点？如何解决？
什么是数制和进位计数制？
数制也称计数制，是指用一组数码符号 和规则来表示数值的方法。 按进位的方法进行计数，称进位计数制， 三个要素：数码、基数和权 例如：十进制数678.34的位权展开式： 678.34 =6×102+7×101+8×100 +3×10-1+4×10-2
思考：
如何快速地将十进制数如456.78(D) 分别转换成二、八、十六进制？
思路:十 规则 八 1化3
8 456 8 57 8 7 0
二 4并1 十六
0 1 7
0.78 8 6. 24 8 1. 92
456.78(D) ≈ 7 1 0 . 6 2(O) =111 001 000.110 010(B) =1,11 00,1 000.110 0,1000 =1 C 8 . C 8(H)
1 0
2 2
0 0
1 1
0.345 2 0.690 2 1.380 2 0.760 2 1.520 2
1.04
十进制转化成r进制

数制及其转换

1
数制的基本概念
2
数制转换
进位计数制
使用有限个基本数码来表示数据，按进位的方法进行 计数，称为进位计数制，简称数制。
• 数码：用不同的数字符号来表示一种数制的数值。 • 基数：某种进位计数制所使用数码个数n，当大于n
时必须进位。 • 位权：一个数字符号处在某个位上所代表的数值是其
本身的数值乘以所数位的一个固定的常数，这个不同 位数的固定常数称为位权。
110101
不同进制数之间的转换
1. 十进制转换成二、八、十六进制
小数转换法 “乘基取整”：用转换机制的基数乘以小数部分，直至小数为0或达到转换精 度要求的位数，每乘一次取一次整数，从最高位排到最低位。
如：（0.625）10=（ 0.101 ）2=（ 0.5 ）8 = （ 0.A ）16
0.625
1.十进制D
• 数码：0~9 基数：10 位权：10i-1、10-i 规则：逢十进一
例： 123.456=1*102+2*101+3*100+4*10-1+5*10-2+6*10-3
2.二进制B
• 数码：0和1 基数：2 位权：2i-1、2-i 规则：逢二进一
例：（110.011）2=1*22+1*21+0*20+0*2-1+1*2-2+1*2-3
3.八进制O
• 数码：0~7 基数：8 位权：8i-1、8-i 规则：逢八进一
例：（123.456）8=1*82+2*81+3*80+4*8-1+5*8-2+6*8-3
4.十六进制H
• 数码：0~9、A~F 基数：16 位权：16i-1、16-i 规则：逢 十六进一
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

阶码的位数决定了表示数的范围； 尾数的位数决定了所表示数的精度；
３、机器数的表示
在计算机中对带符号数的表示方法有原码、补码和反码三种形式。 1）原码 规定符号位用数码0表示正号，用数码1表示负号， 数值部分按一般二进制形式表示数的绝对值。 ＋7: 00000111 ＋0: 00000000 零有两种表示方法
例 3：将 ( 237 . 625 ) 10 转化成二进制
整数： 除2取余 2 |2 3 7 2 |1 1 8 2 |5 9 2 |2 9 2 |1 4 2 |7 2 |3 2 |1 0
1 0 1 1 0 1 1 1
取 值 方 向
小数： 乘2取整 0. 6 2 5 × 2 1 1. 2 5 0 0. 2 5 × 2 0 0. 5 0 × 2 1 1. 0
M

k
Di N
i
i m 1
其中D i为数制采用的基本数符; Ni为权；N为基数
M

k
Di N
i
i m 1
例：十进制数，3058.72 可表示为： 3×103+0×102+5×101+8×100+ 7×10-1+2×10-2 例： 二进制数10111.01 可表示为： 1×24+0×23+1×22+1×21+1×20+0×2-1+1×2-2
－7: 10000111
－0:10000000
３、机器数的表示
在计算机中对带符号数的表示方法有原码、补码和反码三种形式。
２）反码
规定正数的反码和原码相同， 负数反码是对该数的原码除符号位外各位求反
＋7: 00000111 －7: 11111000
＋0: 00000000 零有两种表示方法 －0: 11111111
逻辑乘法 ×或∧（与运算）
例如： 0×0=0 0×1=0 1×0=0 1×1=1 或表示成 0 ∧ 0=0 0 ∧ 1=0 1 ∧ 0=0 1 ∧ 1=1
逻辑非运算 ˉ
对0取非，则为1；对1取非，则为0；
逻辑异或运算
若两个数相同，值为0；不同，则为1； 即 0 0=0；0 1=1；1 1=0。
一直乘到小数部分为零；若遇乘N后，小数部 分的积永不为零，则取有限位作为近似值；
计算机中十进制小数转换为N进制小数时，有时会带来误差。
注意：十进制小数乘2取整法，一般乘到积的小数 部分为0，但有时乘2取整后，小数部分的乘积永 不为0，此时可根据精度要求取有限位作为近似值， 因此计算机中十进制小数转换为二进制小数有时 会带来误差。
如一个32位 浮点数，阶 码用8位表 示，尾数用 24位规格化 补码表示
0
11
0
110011
0 0000011 0 11001100000000000000000
例：假设机器字长为16位，符号位为1位， 阶码4位，尾数12位 +101.1101=0.1011101×211， 其浮点数存放形式为 0 011 0 10111010000
二进制数的逻辑运算
例：若A=（1011）2 ，B=（1101）2 ， 求A∨B；A∧B；Ā；的值。
1011
∨
1011
∧
1101 1111
1101 1001
A∨B=（1111）2；A∧B=（1001）2；
四、二进制数在计算机中的表示
1、真值和机器数 1）、机器数 2）、真值数 3）、溢出 4）、数的范围 机器数表示的范围受到字长和数据类型的限定 用八位字长表示一个整 数，则最大正数为 01111111，即127。若 超出127，则溢出。
例如 (0.1)10=(0.000110011001100..)2 取有限位(0.1)10=(0.000110011)2
十进制数转换为二进制数
整数的转换可采用除2取余法，即把要转换 的十进制数的整数部分不断除以2，并记下 每次除所得余数，直到商为0为止，将所得 余数，从最后一次除得余数读起，就是这个 十进制整数所对应的二进制整数。小数部分 的转换采用乘2取整法，被转换的小数部分， 每次相乘后，所得乘积的整数部分就为对应 的十进制数，将所得小数从第一次乘得整数 读起，就是这个十进制小数所对应的二进制 小数。
数制及其转换
一、进位计数制
1、定义：在采用进位计数的数字系统中，如果只 用N个基本符号（如：0、1、2、…、N-1）表示数值， 则称为基N数制
N称为该数制的基数
举例：N=10 指常用的十进制，符号0、1、2、3、4、5、6、7、8、9 举例：N=2 基本的符号为0和1，为二进制
2、进位计数制有两个基本特点： 由0、1、2、…、N-1这N个数组成 逢N进一，基数为N 如：十进制数逢十进一。二进制数逢二进一 左移一位扩大N倍（相当于乘N），右移一 位缩小N倍（相当于除N） 采用位权表示法。 任意一位N进制数M可表示为：
3）补码
正数的补码与原码相同，负数补码则先对该数的原 码除符号外各位取反，然后末位加１． ＋7: 00000111 －7: 11111001 ＋0: 00000000 －0: 00000000
N2= 1000100 [N2]原=11000100 [N2]反=10111011 [N2]补=10111100
例1：
( 207 . 1) 8 2 8 0 8 7 8 1 8
2 1 0 1
(135 . 125 ) 10
例2：求（1100101.101）2 的等值十进制 （1100101.101）2 =1×26+1×25+0×24+0×23+1×22 +0×21+1×20+1×2-1 +0×2-2+1×2-3 =64+32+0+0+4+0+1+0.5+0.125 =（101.625）10 即 （1100101.101）2=（101.625）10
任何一种数制表示的数都可以写成按位 权展开的多项式之和。
3、几种常用的进位计数制
十进制
•0 •1 •2 •3 •4 •5 •6 •7 •8 •9 •10 •11 •12 •13 •14 •15 •16
二进制
0 1 10 11 100 101 110 111 1000 1001 1010 1011 1100 1101 1110 1111 10000
八进制
0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17 20
十六进制
0 1 2 3 4 5 6 7 8 9 A B C D E F 10
二、数制的相互转换
1、N进制转换为十进制
方法： 将N进制数按权展开运算后，可得到十进制数
M

k意：数位ｉ的确定不要弄错
3、非十进制数间的转换
注意：
在整数转换中，是从小数点开始，由右往 左确定二进制的三位（或四位），取后不够， 则在数码前补0，添足位数。 在小数转换中，是从小数点开始，由左往右 确定二进制的位数，取后不够，在末位补0，添 足位数。
数制之间的转换
例5 将（741.566）8转换成为二进制数 解 （741.566）8= （111100001.101110110）2 例6 将（1011010.10111）2转换为十六进制数 解 （1011010.10111）2 =（01011010.10111000）2 =（5A.B8）16 即 （1011010.10111）=（5A.B8）16
二进制数的逻辑运算
逻辑值只有两个“T”与“F”或“Y”与 “N”；我们知道，二进制数也只有两个 值 “1”与“0”，所以可用二进制数表示逻辑 值，并充分利用逻辑运算的特点，快速地 进行信息的处理。 注意：运算按位进行，没有进位和借位。
二进制数的逻辑运算
逻辑加法 +或∨（或运算）
例如： 0+0=0 0+1=1 1+0=1 1+1=1 或表示成 0∨0=0 0∨1=1 1∨0=1 1∨1=1
零有唯一编码
例： N1=+1000100，
则[N1]原=01000100 [N1]反=01000100 [N1]补=01000100
3、非十进制数间的转换
二进制、八进制与十六进制之间的互换 八进制 → 十六进制 (通过二进制转换) 1位八进制 = 3 位二进制 1位十六进制 = 4 位二进制 方法：通过扩展法，把八进制→二进制 再通过收缩法，把二进制→十六进制
如：162 ) 8 ( 001 ,110 , 010 ) 2 (1110010 ) 2 ( 如：1110010 ) 2 ( 0111 , 0010 ) 2 ( 72 ) 16 (
则 ( 237 . 625 ) 10 ( 355 . 5 ) 8
题目： 1、（25）10 =（ 11001 ）2 ？
2、（101A）16=（ 4122 ）10 ？
3、（0.3125）１０＝（
0.0101 ？
）２
3、非十进制数间的转换
方法：一般采用上述方法的结合。
N1进制 按 权 展 开 十进制 整：除N2取余 小：乘N2取整 N2进制
则 ( 237 . 625 ) 10 (11101101
. 101 ) 2
例 4：将 ( 237 . 625 ) 10 转化成八进制
进位计数制 0. 6 2 5 数制间转换 × 8 5 5. 0 0 0
整 数： 除8取余
8 |2 3 7 8 |2 9
余
5 5
数
低位 高位
8 |3 0
3
小 数：乘8取整
三、数制运算
各种数制都有算术运算规则(加、减、乘、 除)； 二进制数独有逻辑运算，又是计算机唯 一识别和处理的数，所以，我们选取二进制 数作为讲解的主要对象。