第三章 时域分析

eT
T
c(t )

1
t2
Tt
T 2 (1
t
eT
)
2
§3 二阶系统的时域分析
二阶系统的定义：用二阶微分方程描述的系统 微分方程的标准形式：
d 2 c(t ) dt 2

2 n
dc(t) dt

n 2 c(t )

n 2 r (t )
—阻尼比，n —无阻尼自振频率。
传递函数及方框图
d 1 2
cos d t p )
0
- n (cos d t p
1 2
sin d t )
d (-sin d t p
d 1 2
cos d t p )
0
sin d t p 0, d t p 0, ,2 ,3 .......
R(s) Ts 1
1 TS 1
一．单 位 阶 跃 响 应
r(t) 1(t) R(s) 1 s
C(s) (s)R(s) 1 1 1 T Ts 1 s s Ts 1
t
c(t) 1 e T
说明:
1.可以用时间常数去度量系统输出量的数值
t t

T时, c(t) 1 e1 0.632 3T时, c(t) 0.95 95%
好 等 于c(), 令N m , 得 2
n
N
1 2 t s arctg
1 2



2
将t s

1
n
ln
1 代入,并取整数得
1- 2
N N(
1- 2 2
ln
1

第3章时域分析法基本要求3－1 时域分析基础3－2 一、二阶系统分析与计算3－3 系统稳定性分析3－4 稳态误差分析计算返回主目录基本要求1熟练掌握一、二阶系统的数学模型和阶跃响应的特点。

熟练计算性能指标和结构参数，特别是一阶系统和典型欠阻尼二阶系统动态性能的计算方法。

2了解一阶系统的脉冲响应和斜坡响应的特点。

3正确理解系统稳定性的概念，能熟练运用稳定性判据判定系统的稳定性并进行有关的参数计算、分析。

4正确理解稳态误差的概念，明确终值定理的应用条件。

5熟练掌握计算稳态误差的方法。

6掌握系统的型次和静态误差系数的概念。

控制系统的数学模型是分析、研究和设计控制系统的基础，经典控制论中三种分析（时域，根轨迹，频域）、研究和设计控制系统的方法，都是建立在这个基础上的。

3－1 时域分析基础一、时域分析法的特点它根据系统微分方程，通过拉氏变换，直接求出系统的时间响应。

依据响应的表达式及时间响应曲线来分析系统控制性能，并找出系统结构、参数与这些性能之间的关系。

这是一种直接方法，而且比较准确，可以提供系统时间响应的全部信息。

二、典型初始状态，典型外作用1. 典型初始状态通常规定控制系统的初始状态为零状态。

即在外作用加于系统之前，被控量及其各阶导数相对于平衡工作点的增量为零，系统处于相对平衡状态。

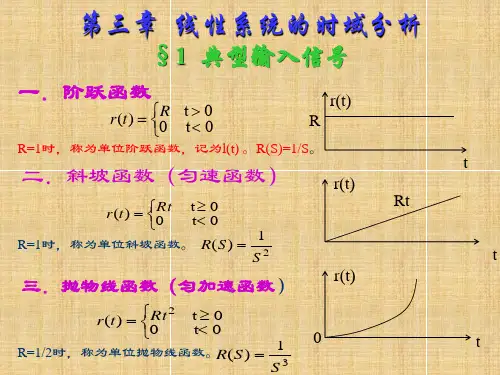
2. 典型外作用①单位阶跃函数1(t)tf(t)⎩⎨⎧<≥==0t 00t 1)t (1)t (f 其拉氏变换为：s 1dt e 1)s (F )]t (f [L 0st===⎰∞-其数学表达式为：t②单位斜坡函数0t 0t 0t)t (1t )t (f <≥⎩⎨⎧=.=其拉氏变换为：2sts 1dt e t )s (F )]t (f [L ===⎰∞-f(t)其数学表达式为：③单位脉冲函数000)()(=≠⎩⎨⎧∞==t t t t f d 其数学表达式为：其拉氏变换为：1)()]([==s F t f L ⎰+∞∞-=1)(dt t d 定义：图中1代表了脉冲强度。

解 ： h(k)满足h(k) – h(k –1) – 2h(k –2)=δ(k) –δ(k –2) 令只有δ(k)作用时，系统的单位序列响应h1(k) , 它满足 h1(k) – h1(k –1) – 2h1(k –2)=δ(k) 根据线性时不变性，
h(k) = h1(k) – h1(k – 2) =[(1/3)(– 1)k + (2/3)(2)k]ε(k) – [(1/3)(– 1)k –2 + (2/3)(2)k–2]ε(k – 2)
f (i)h(k i) ai (i)bki (k i)
i
i
当i < 0,ε(i) = 0；当i > k时，ε(k - i) = 0
1
a
k
1
yzs
(k
)
k i0
aibk
i
(k
)
bk
k i0
a b
i
(k
)
bk
bk
b 1 a
b (k 1)
注：ε(k)*ε(k) = (k+1)ε(k)
当ik时ki0???????????????iikiiikbiaikhif?????????????????????????????????????????????????bakbbabababkbabkbakykkkkiikkiikizs111100??注
《信号与系统》 第三章 离散系统的时域分析
λ n + an-1λn– 1 + … + a0 = 0 其根λi( i = 1，2，…，n)称为差分方程的特征根。 齐次解的形式取决于特征根。
参看教材第87页 表3-1。
2. 特解yp(k): 特解的函数形式与激励的函数形式有关

例3.1-2 描述一阶LTI系统的常系数微分方程如 式（3.1-3）所示
设 f (t) 2 a 2, b 1 则有
dy(t) 2 y(t) 2 dt
已知初始值 y(0) 4 求 t 0时系统的响应 y(t)
解：第一步，由方程可知系统的特征方程为 2 0
2 由此可得系统的齐次解为
2
处理教研室
第三章 连续信号与系统的时域分析
教学重点：
1、常微分方程的建立及其解的基本特点； 2、阶跃响应和冲激响应的概念； 3、卷积及其在系统分析中的应用。
2020/6/7
信号
3
处理教研室
应用实例：汽车点火系统
汽车点火系统主要由电源（蓄电池和发电机）、电阻、 点火开关、点火线圈、分压器等组成。
系数 a,b都是常量。系统的阶数就是其数学模型——
微分方程的阶数。
而 n 阶常系数线性微分方程的一般形式为
an
dn y(t) dt n
an1
dn1 y(t) dt n1
L
a1
dy(t) dt
a0
y (t )
bm
dm f (t) dt m
bm1
dm1 f (t) dt m1
L
b1
df (t) dt
b0
即yf’(0+) = yf’(0-) = 0，yf(0+) = yf(0-) = 0
对t>0时，有 yf”(t) + 3yf’(t) + 2yf(t) = 6
不难求得其齐次解为Cf1e-t + Cf2e-2t，其特解为常数3，
于是有
yf(t)=Cf1e-t + Cf2e-2t + 3
代入初始值求得

系统响应达到峰值所需要的时间。
调节时间
系统响应从峰值回到稳态值所需的时间。
振荡频率
系统阻尼振荡的频率，反映系统的动态性能。
系统的阶跃响应与脉冲响应
阶跃响应
系统对阶跃输入信号的响应，反映系 统的动态性能和稳态性能。
脉冲响应
系统对脉冲输入信号的响应，用于衡 量系统的冲激响应能力和动态性能。
03
一阶系统时域分析
01
单位阶跃响应是指系统在单位阶跃函数作为输入时的
输出响应。
计算方法
02 通过将单位阶跃函数作为输入，代入一阶系统的传递
函数中，求出系统的输出。
特点
03
一阶系统的单位阶跃响应是等值振荡的，其最大值为1，
达到最大值的时间为T，且在时间T后逐渐趋于0。
一阶系统的单位脉冲响应
定义
单位脉冲响应是指系统在单 位脉冲函数作为输入时的输
无法揭示系统结构特性
时域分析法主要关注系统的动态行为和响应，难以揭示系统的结构特 性和稳定性。
对初值条件敏感
时域分析法的结果对系统的初值条件较为敏感，初值条件的微小变化 可能导致计算结果的较大偏差。
感谢您的观看
THANKS
计算简便
时域分析法通常采用数值积分方法进 行计算，计算过程相对简单，易于实 现。
时域分析法的缺点
数值稳定性问题
对于某些系统，时域分析法可能存在数值稳定性问题，例如数值积分 方法的误差累积可能导致计算结果失真。
计算量大
对于高阶系统和复杂系统，时域分析法需要进行大量的数值积分计算， 计算量较大，效率较低。
自动控制原理-第3章-时域 分析法
目录
• 时域分析法概述 • 时域分析的基本概念 • 一阶系统时域分析 • 二阶系统时域分析 • 高阶系统时域分析 • 时域分析法的优缺点

SNRdB 6.02B 4.77 20log10 (
x
xmax
)
(3-11)
3.1 语音信号的短时处理方法 脉冲编码调制
若是xmax取为4倍方差(δx)
SNRdB 6.02B 7.27
取样之位数 8 16 24
(3-12)
数字信号的信噪比 41 dB 89 dB 137 dB
3.1 语音信号的短时处理方法 脉冲编码调制
一个数字信号取样之后，变成离散时间信号，接下来就是要用数字 方式来表示这个离散时间信号上的每个取样值。 一个电位波形会有固定的电压范围，一个取样值可以是在此电压范 围内的任何电位。如果只能用固定数目的位来表示这些取样值，那 么这些二进数字就只能代表固定的几个电位值，这个转换就是量化 (quantization)，而转换之后只允许存在的几个电位值就是量化阶 数(quantization level)。 执行量化转换的硬件电路，就是量化器（quantizer)。以二进数字 表示的信号就是数字信号(digital signal)，而这种将信号波形转 变成二进数字的方法，就叫脉冲编码调制(pulse code modulation, PCM)。
3.1 语音信号的短时处理方法
预处理 平滑滤波器：D/A后面的低通滤波器是平滑滤 波器，对重构的语音波形的高次谐波起平滑 作用，以去除高次谐波失真。 预加重：




现象:由于语音信号的平均功率谱受声门激励和口 鼻辐射的影响，高频端大约在800 Hz以上按6dB/ 倍频程跌落，为此要在预处理中进行预加重。 目的:提升高频部分，使信号的频谱变得平坦，以 便于进行频谱分析或声道参数分析。 位置:预加重可在A/D变换前的反混叠滤波之前进行， 这样不仅能够进行预加重，而且可以压缩信号的动 态范围，有效地提高信噪比。

响应曲线如图3-2所示。图中
为输出的稳态值。
第三章 线性系统的时域分析 法
图 3-2 动态性能指标
第三章 线性系统的时域分析 法
动态性能指标通常有以下几种:
延迟时间td: 指响应曲线第一次达到稳态值的一半所需的时间
上升时间tr: 若阶跃响应不超过稳态值, 上升时间指响应曲线从 稳态值的10%上升到90%所需的时间; 对于有振荡的系统, 上升时 间定义为响应从零第一次上升到稳态值所需的时间。上升时间越 短, 响应速度越快。
可由下式确定: (3.8)
振荡次数N: 在0≤t≤ts内, 阶跃响应曲线穿越稳态值c(∞)次 一半称为振荡次数。
上述动态性能指标中, 常用的指标有tr、ts和σp。上升时间tr 价系统的响应速度; σp评价系统的运行平稳性或阻尼程度; ts是同
时反映响应速度和阻尼程度的综合性指标。 应当指出, 除简单的一 、二阶系统外, 要精确给出这些指标的解析表达式是很困难的。
中可以看出, 随着阻尼比ζ的减小, 阶跃响应的振荡程度加剧。 ζ =0时是等幅振荡, ζ≥1时是无振荡的单调上升曲线, 其中临界阻尼 对应的过渡过程时间最短。 在欠阻尼的状态下, 当0.4＜ζ＜0.8时过
渡过程时间比临界阻尼时更短, 而且振荡也不严重。 因此在 控制工程中, 除了那些不允许产生超调和振荡的情况外, 通常都希
第三章 线性系统的时域分析法 4. 脉冲函数 脉冲函数(见图3-1(d))的时域表达式为
(3.4)
式中,h称为脉冲宽度, 脉冲的面积为1。若对脉冲的宽度取趋于 零的极限, 则有
(3.5) 及
(3.6)
称此函数为理想脉冲函数, 又称δ函数(见图3-1(e))。
第三章 线性系统的时域分析 法

对方程两边求拉氏变换：
若
Td Tm Td
s2n(s 0,
)则有Tm：n(s)
n(s)
U
d
(s)
/
Ce
n(s) 1/ Ce
U d (s) 1 Tms
（5）转角的转换环节
设 传动比为 ,电动机转角为m
m , c
c
1
m
又 n dm (t)
dt
n(s) sm (s) c(s) m / 1
1- 2
具体步骤如下：
求阶跃输入下的暂态响应
查表： F (s) s a0
(s a)2 2
则
f (t) L1[F (s)] 1
(a0 a)2 2
1
2 eat sin( t )
arctg
a0 a
由
s2
s 2n 2ns n2
s 2n (s n )2 (n
1 )2
2
1.8
1.6
1.4
1.2
1
0.8
0.6 0.4 0.2
0 0
246
nt
8 10 12
⒊ 当 1时，特征方程有一对相等的负实根，称为临界阻尼
系统，系统的阶跃响应为非振荡过程。
➢当 1 时，
阶跃响应曲线为：
xc
(s)
1 s
s2
n2 2n s
n2
n2 s(s n )2
1 1 n s s n (s n )2
1 )( s
T1
1 T2
)
式中
T1
1 a
n (
1
2
1)
T2
1 b
n (
1
2
1)

16:19
一般的控制系统多数为高阶系统，但是它们有可 能在一定的条件下用二阶系统去近似。因此，对 于二阶系统的分析具有重要的实际意义。在系统 的分析与设计中，通常将二阶系统的响应特性作 为一种基准。
16:19
二阶系统传递函数的标准形式
某随动系统方块图
如图所示随动系统的微分方程式：
TM
d
2c t
/ TM
s2
n2 2ns
n2
3.4.4
其中 n为无阻尼自然振荡角频率(固有频率)； 称为阻尼比；
均为二阶系统的特征参数，是系统本身的固有特性。
16:19
二阶系统的特征方程
s2
2
ns
2 n
0
3.4.5
由上式解得二阶系统的二个特征根(即闭环极点)为：
s1,2 n jn 1 2 3.4.6
当0 1时，特征根为一对实部为
16:19
当-1< <0 ，特征根是位于右半平面的共轭复根，呈发散振荡 状态。如图3 .6(e)所示。
当 < -1，呈单调发散状态。如图3 .6(f)所示 P53图3.7表明了极点分布与n、 的关系图。
16:19
二阶系统的单位阶跃响应 1. 欠阻尼状态
令r t 1t，则有Rs 1
s
二阶系统在单位阶跃函数作用下输出：
16:19
3.1 线性定常系统的时间响应及 暂态响应性能指标
一、时间响应
线性系统的动态方程
an y(n) (t) an1 y(n1) (t) L a1y&(t) a0 y(t) bm x(m) (t) bm1x(m1) (t) L b1x&(t) b0x(t)
经过拉氏变换得

1
1
ቤተ መጻሕፍቲ ባይዱ
s4 3s3 s2 3s 1 0 s3 3 3
试判别该系统的稳定性。 s2 0 1
当 0时,3 3 0,
s1 3 3 0
s0
1
有2个特征根在s平面第右3章边控. 制系系统统的是时域不分析稳定的
10 0 0
(2) 劳斯表中某一行的元素全为零。
——这时系统在s平面上存在一些大小相等符号相反的
61
s0 6
劳斯表中第一列元素大于零，所以该系统是稳定的。 这时，系统所有的特征根均处于s平面的左半平面。
第3章 控制系统的时域分析
课程回顾(1)
1、 稳态性能指标 2、 动态性能指标
ess
lim[r(t)
t
cr (t)]
(1)延迟时间td (2)上升时间tr
(3)峰值时间tp
(4)调整时间ts
负可化为全为正） （2）劳斯表中第一列所有元素均大于零。
第3章 控制系统的时域分析
例3-1 已知三阶系统特征方程为 a0s3 a1s2 a2s a3 0
试写出系统稳定的充要条件
解：列写劳斯表 s3
a0
a2
0
s2
a1
a3
0
s1 a1a2 a0a3 0
a1
s0
a3
0
故得出三阶系统稳定的充要条件为：
0
9
s0 5
s1 32
0
s0 5
所得结论不变
第3章 控制系统的时域分析
2、劳斯稳定判据的特殊情况
(1) 劳斯表中某一行的第一个元素（系数）为零，而该 行其它元不为零。
——计算下一行第一个元素时将出现无穷大，以至劳斯 表的计算无法进行。

位脉冲响应，由此可以求得系统的传递函数。
总结与分析：
一阶系统对典型试验信号的响应 输入信号x(t) 输出响应y(t)
1 2 3
t
1() δ(t)
t T Te t / T
1 et /T
1 T
et /T
l 线性定常系统对输入信号导数的响应，可以通过 把系统对输入信号的响应进行微分求得； l 系统对输入信号积分的响应，可以通过把系统对原 输入信号的响应进行积分求得，而积分常数则由初 始条件决定。
3.1.1 控制系统的输入信号
● 在分析和设计控制系统时，需要有一个对各种
系统性能进行比较的基础。
● 从实际应用中抽象出一些典型的输入信号，它
们具有广泛的代表性和实际意义。
● 通过比较各类系统对这些典型试验信号的响
应来分析它们的性能。
常用的典型试验信号：
r(t) A t (a) 阶跃信号
r(t)
1 E
实验方法求取一阶系统的传递函数：
63.2％ T
1 Ts 1
对一阶系统的单位阶跃响应曲线， 1、直接从达到稳态值的63.2%对应的时间求出一阶 系统的时间常数；
2、从t＝0处的切线斜率求得系统的时间常数。 思考题：
若系统增益K不等于1，系统的稳态值应是多少？如何用实
验方法从响应曲线中求取K值？
3.2.2单位斜坡响应
2、系统的稳态响应为y(∞)=t－T，是一个与输入斜 坡函数斜率相同但时间迟后T的斜坡函数。
3、输出总是小于输入，误差逐步从零增大到时间 常数T并保持不变，因此T也是稳态误差。系统 的时间常数T越愈小，系统跟踪输入信号的稳态 误差也越小。
3.2.3 单位脉冲响应
1 R( s) L[ ( t )] 1 Y ( s) G ( s) R( s) G (s ) Ts 1 系统输出量的拉氏变换式就是系统的传递函数

时，系统的输出状态。研究系统的稳态特性，以确定输出信 号对输入信号跟踪（伺服、复现）能力。稳态过程又称稳态 响应，其稳态性能用稳态误差描述。
稳定性指标（收敛、发散）
稳定是控制系统能够工作的首要条件，只有动态过程收 敛 (响应衰减)，研究动态性能与稳态性能才有意义。
收敛是指系统从一个状态运动到另一个状态，在其动态响应过 程中，振荡逐渐减弱并稳定在某一状态。反之则称为发散。
T
量衰减为零。在整个工作时间内，系统的响应都
不会超过其稳态值。由于该响应曲线具有非振荡
特征，故也称为非周期响应。
1 斜率 1
T 0.632
C(t) 0.95
T
3T
图中响应曲线的初始斜率（t=0时）为 1/T。如果系统保 持初始响应的变化速度不变，则当t=T时，输出量就能达 到稳态值。实际上，响应曲线的斜率是不断下降的，经
过T时间后，输出量c(t)从0上升到稳态值的63.2%。经过 3T-4T时， c(t)将分别达到稳态值的95%-98%。可见，时 间常数T反应了系统的响应速度，T越小，输出响应上升 越快，响应过程的快速性也越好。
c(t) 1 exp( t ) T
由上式可知，只有当t趋于无穷大时，响应的瞬 态过程才能结束，在实际应用中，常以输出量达到 稳态值的95%或98%的时间作为系统的响应时间 （即调节时间），这时输出量与稳态值之间的偏差 为5%或2%。
t
c(t)
c(t) 1 e T
ess
lim
t
e(t)
0
1
1 T
0.632
动态性能指标：
63.2% 86.5% 95% 98.2% 99.3%
td 0.69T tr 2.20T
t

第3章 控制系统时域分析电气信息学科世界著名学者诺伯特·维纳(Norbert Wiener，1894～1964)维纳是美国数学家，控制论的创始人.1948年维纳发表《控制论》，宣告了这门新兴学科的诞生. 这是他长期艰苦努力并与生理学家罗森勃吕特等人多方面合作的伟大科学成果. 维纳立即从声誉有限的数学家一跃成为一位国际知名人士．维纳是一个名符其实的神童．他三岁半开始读书，生物学和天文学的初级科学读物就成了他在科学方面的启蒙书籍，七岁时，开始深入物理学和生物学的领域，甚至超出了他父亲的知识范围．维纳于15岁时获得塔夫茨学院数学系学士学位，并于18岁获哈佛大学哲学博士学位．他先后留学于英国剑桥大学和德国哥丁根大学，在罗素、哈代、希尔伯特等著名数学家指导下研究逻辑和数学．1924年维纳升任助理教授，1929年升为副教授，由于在广义调和分析和关于陶伯定理方面的杰出成就，1932年晋升为正教授．维纳在其50年的科学生涯中，先后涉足哲学、数学、物理学和工程学，最后转向生物学，在各个领域中都取得了丰硕成果，称得上是恩格斯颂扬过的、本世纪多才多艺和学识渊博的科学巨人．他一生发表论文240多篇，著作14本．主要著作有《控制论》(1948)、《维纳选集》(1964)．维纳还有两本自传《昔日神童》和《我是一个数学家》．他的主要成果有如下八个方面：建立维纳测度；引进巴拿赫—维纳空间；阐述位势理论；发展调和分析；发现维纳—霍普夫方法；提出维纳滤波理论；开创维纳信息论；创立控制论． 1933年，维纳由于有关陶伯定理的工作与莫尔斯分享了美国数学会五年一次的博赫尔奖．同时，他当选为美国科学院院士．1934年，维纳应邀撰写了《复域上的傅立叶变换》．不久，他当选为美国数学会副会长．1959年，维纳从麻省理工学院退休。

1964年1月，他由于“在纯粹数学和应用数学方面并且勇于深入到工程和生物科学中去的多种令人惊异的贡献及在这些领域中具有深远意义的开创性工作”荣获美国总统授予的国家科学勋章．维纳是伽金汉基金会旅欧研究员，富布赖特研究员，英、德、法等国的数学会会员，但任过中国、印度、荷兰等国的访问教授．3.1 引言系统的时域分析指对控制系统的稳定性、暂态性以及稳态性能分析．稳定性是控制系统工作的前提，不稳定的系统没有任何工程价值．对于不同的系统，例如线性的、非线性的、定常的、时变的系统，稳定性的定义也不同，本章仅讨论线性定常单输入单输出系统的稳定性．从控制系统分析和设计的角度来说有绝对稳定性和相对稳定性，绝对稳定指系统是否稳定，一旦系统是稳定的，则人们更关心其稳定的程度，这就是相对稳定性，相对稳定性一般用稳定裕度衡量. 当系统受外加作用时引起的输出随时间的变化规律，称其为系统的时域响应，分为暂态响应和稳态响应．暂态响应是指系统输出量当时间趋于无穷时趋于零的那部分时间响应，工程上一般定义暂态响应为从初始状态到达某一规定值（例如偏离终值的误差值在终值的5%或2%以内）并且以后不再超过此值的这一部分时间响应过程，它反映控制系统的快速性和阻尼程度，由于系统物体的惯性都是无法避免的，因此人们常常可以观察到暂态现象．而稳态响应则是整个响应在暂态响应消失后余下的那部分响应，主要指系统输出量的最终位置，它反映控制系统的准确性或控制精度，控制系统是按照稳态误差和误差系数的计算来表示控制精度的．本章主要分析了一阶和二阶线性定常系统的典型输入信号激励下的时域响应以及对应的时域性能指标，详细介绍了单输入单输出线性定常系统的稳定性判断的劳斯－赫尔维茨判据，也对稳定的控制系统的稳态误差以及误差系数的分析计算做了详细的叙述，介绍了提高控制系统精度的一般工程方法．对高阶线性系统的分析在一定条件下可以用主导极点的模型降阶方法来近似．本章还介绍了如何利用MATLAB工具分析线性系统的性能．3.1.1 典型输入信号控制系统性能评价分为暂态性能指标和稳态性能指标两大类．对于同一系统，在不同的输入信号作用下会产生不同的输出响应， 因此为了求解系统的时间响应，必须了解输入信号的解析表达式. 然而，在一般情况下，控制系统的外加输入信号具有随机性而无法预先确定．因此，在分析和设计控制系统时，需要有一个对控制系统的性能进行比较的基准，这个基准就是系统对预先规定的具有典型意义的实验信号激励下的响应．为了评价控制系统的性能，需要选择若干个典型输入信号．另外，一个复杂的信号通常可看作是几个简单典型信号的合成.所谓典型输入信号，是指控制系统分析与设计中常常遇到的一些输入信号，也是在数学描述上加以理想化的一些基本输入函数．选取典型信号应满足如下条件，首先，输入信号的形式应反映系统响应的实际输入；其次，输入信号在形式上应尽可能的简单，应当是实验室或仿真可以获得以便于对系统响应进行分析的信号；另外，应选取能使系统工作在最不利情况下的激励信号作为输入信号．控制系统中常用的典型输入信号有：单位阶跃函数、单位斜坡（速度）函数、单位抛物线（加速度）函数、单位脉冲（冲激）函数和正弦函数等，如表3.1所示．表3.1 常用典型输入函数3.1.2 时域性能指标稳定是系统工作的前提，只有系统是稳定的，分析系统的暂态和稳态性能以及性能指标才有意义．控制系统时域性能指标（Time Response Specifications）分为暂态与稳态性能指标．1. 暂态性能指标一般认为阶跃输入对系统来说是最严峻的工作状态，如果系统在阶跃函数作用下的暂态 性能满足要求，那么系统在其它形式函数作用下其暂态性能也是令人满意的．为此，通常在阶跃函数作用下，测定或计算系统的暂态性能．描述稳定的系统在阶跃函数作用下暂态过程随时间t 的变化状况的指标，称为暂态性能指标．如图3.1所示为某一控制系统的阶跃响应，其暂态性能指标定义如下：1）调节时间 (settling time ) s t ：指阶跃响应到达并保持在终值的±5%（或±2%）的 误差带内所需时间．2）峰值时间 (peak time) p t ：响应超过其终值到达第一个峰值所需时间．3) 上升时间 (rise time) r t ：响应从终值的10%上升到终值的90%所需时间. 对振荡系 统, 工程上上升时间r t 定义为输出从零到第一次上升至终值所需时间.4）超调量 (peak overshoot) %σ：响应的最大峰值与终值的差与终值比的百分数，即： ()()%100%()p c t c c σ-∞=⨯∞ （3.1） 超调量常常用来衡量控制系统的相对稳定性或阻尼程度，一般不希望控制系统有很大的超调．在实际应用中，以上四个指标可以用来衡量控制系统的暂态特征，一般通过测量系统的阶跃响应，很容易得到这些指标．通常，用p t 或r t 评价响应速度；用%σ评价系统的相对稳定程度或阻尼程度；用s t 同时反映响应速度和阻尼程度的综合性指标．除简单的一、二阶(0.9(c c ∞∞0.1(c ∞图 3.1 时域性能指标系统外，要精确确定这些暂态性能指标的解析表达式是很困难的．2. 稳态性能指标稳态误差ss e 是衡量系统控制精度或抗扰动能力的一种度量．工程上指控制系统进入稳态后（t →∞）期望的输出与实际输出的差值，ss e 越小，控制精度越高．3.2 控制系统时域分析3.2.1 一阶系统的时域分析可以用一阶微分方程描述的系统，称为一阶系统．一阶系统在控制工程实践中十分常见，有些高阶系统的特性，常可用一阶系统的特性近似表征．考察如图3.2所示的RC 电路，()c t 是电容器C 的输出电压．该电路系统的数学模型为一阶常微分方程：()()()dc t T c t r t dt+= 其中，T RC =为时间常数，控制系统方框图如图3．3所示 ．其传递函数为： ()1()()1C s s R s TsΦ==+ (3.2) 1. 一阶系统的单位阶跃响应当输入信号为单位阶跃信号()1r t =()t , t ≥0时，系统的响应()c t 称为单位阶跃响应．将单位阶跃输入的像函数()1/R s s =代入式(3.2)，并对输出取拉普拉斯反变换得到该一阶系统的单位阶跃响应：()1t T c t e -=-， t ≥0 (3.3)图 3.3 RC 电路方框图))t r 图 3.2 RC 电路由式(3.3)绘出的系统单位阶跃响应为以指数规律上升到终值1的曲线，如图 3.4 所示．其中，()0.632c T =；(2)0.865c T =；(3)0.950c T =；(4)0.982c T =．显然按照5%或2%的误差带准则有调节时间(3s t =～4)T （5% ～2%误差带），而p t ，%σ不存在． 综上所述，时间常数T 反映系统响应过程的快慢，T 越小，系统响应越快；反之，系统响应越慢．2. 一阶系统的单位脉冲响应当输入信号为单位脉冲或单位冲激信号()()r t t δ=时，系统的响应称为单位脉冲或单位冲激响应．因为理想单位脉冲函数的拉普拉斯变换为1，所以单位脉冲响应的拉普拉斯变换与系统的闭环传递函数相同，即：()()1()()()1r t t C s s R s Tsδ==Φ=+ 两边进行拉普拉斯反变换，得： 1()t T c t e T-= (3.4) 由式（3.4）可知，一阶系统的单位脉冲响应是非周期的单调递减函数，当0t =时，响应取最大值1/T ；当t →∞时，响应的幅值衰减为零．根据给出的误差带宽度可以求出调节时间s t ，通常取 (3s t =～4)T ．一阶系统的单位脉冲响应如图 3.5 所示．图 3.4 一阶系统单位阶跃响应 t3. 一阶系统的单位斜坡响应当输入信号为单位斜坡或速度信号()r t t =，t ≥0时，系统的响应称作单位斜坡响应．因为单位斜坡输入的拉普拉斯变换像函数为2()1/R s s =，所以由拉普拉斯反变换得到该一阶系统的单位斜坡时域响应表达式为： ()()t T c t t T Te -=-+ (3.5)式(3.5)表明，一阶系统的单位斜坡响应可分为暂态分量和稳态分量两个部分，其中t T Te -为暂态分量，随时间的增加而逐渐衰减为零；t T -为稳态分量．一阶系统的单位斜坡响应如图 3.6所示．一阶系统单位斜坡响应的稳态误差lim(()())ss t e r t c t T →∞=-=，T 越小跟踪准确度越高．4. 一阶系统的单位抛物线响应当输入信号为单位抛物线或单位加速度信号2()/2r t t =，t ≥0时，因为单位抛物线输入信号拉普拉斯变换像函数为3()1/R s s =，所以由拉普拉斯反变换求得一阶系统的单位抛图 3.5 一阶系统单位脉冲响应t32 T 图 3.6 一阶系统单位斜坡响应物线的时域响应表达式为：221()(1)2t T c t t Tt T e -=-+- (3.6) 系统跟踪误差为：2()()()(1)t T e t r t c t Tt T e-=-=-- 因此lim ()t e t →∞=∞，即跟踪误差随时间增大而增大直至无穷大，故一阶系统不能实现对加速度输入函数的跟踪．3.2.2 典型二阶系统的时域分析如果动态系统的数学模型为二阶微分方程的系统，统称为二阶系统．在控制工程中，二阶系统应用广泛，而且许多高阶系统在一定条件下，可以近似用二阶系统的特性来表征．因此，二阶系统的性能分析，在自动控制理论中有着重要的地位．第2章分析的位置随动系统，其简化的数学模型为22c c m c r d d T K K dt dtθθθθ++= 闭环传递函数为2()()()c r m s K s s T s s KθθΦ==++ 将上式化为标准的典型二阶系统形式：222()()()2n n nC s s R s s s ωξωωΦ==++ (3.7) 其相应的方框图如图 3.7所示，其中，无阻尼振荡频率 （Undamping natural frequency）n ω= ，阻尼比（Damping factor）ξ=．典型二阶系统特征方程为：)s (R s 图 3.7 典型二阶系统2220n n s s ξωω++= (3.8)于是有特征根为：1,2n n d d s j j ξωωξωωσω=-±=-±=-± (3.9) 其中，特征根的实部为n σξω=，阻尼振荡频率（Damped natural frequency）d ωω=(1)ξ<．1. 典型二阶系统的单位阶跃响应典型二阶系统特征根的性质主要取决于ξ值的大小，ξ值的大小决定了系统阻尼程度．ξ在不同范围取值时，二阶系统的特征根在s 平面上的位置不同，典型二阶系统的时间响应对应着不同的运动规律．1）欠阻尼(01ξ<<)此时典型二阶系统在左半s 平面有一对共轭复根, 如图3.8 (a)所示．当输入为单位阶跃信号()1/R s s =时，由式(3.7)得到：222222211()2()()n n n n n n dn d s C s s s s s s s ωξωξωξωωξωωξωω+=⋅=--++++++两边分别取拉普拉斯反变换得：()1[cos ]n t d d c t e t t ξωωω-=-+1sin()n t d t ξωωβ-=+，0t > (3.10)其中, arctan β= 或 cos arc βξ=．式(3.10)表明，欠阻尼典型二阶系统的单位阶跃响应由两部分组成：稳态响应分量为1，表明典型二阶系统在单位阶跃函数作用下不存在稳态误差；暂态分量为阻尼正弦振荡项，其振荡频率为d ω．暂态分量衰减的快慢程度取决于包络线1n tξω-±对应的典型二阶系统欠阻尼情况下的单位阶跃响应如图3.8 (b)所示。

2时 5时
h(t)
其他动态性能指标：
td 0.69T
tr 2.20T
ts 3T (5%误差带）
16 t
3-2 一阶系统的时域分析
自控原理
3.一阶系统单位脉冲响应
当输入信号为理想单位脉冲函数δ (t)时，R(S)＝1，输出量的拉氏
变换与传递函数相同，即 C(s) 1 TS 1
t
eT
)
t0
2
S3
2
上述几种典型响应有如下关系：
积分
积分
积分
单位脉冲
单位阶跃
单位斜坡
函数响应
函数响应
函数响应
微分
微分
微分
单位抛物线 函数响应
20
3-2 一阶系统的时域分析
自控原理
例: 设某高阶系统可用下列一阶微分方程近似描述：


T ct ct rt rt
其中， 1 (T ) 0
结论：一阶系统无法跟踪加速度形式的输入信号
19
3-2 一阶系统的时域分析
自控原理
输入信号 输入信号
时域
频域
输出响应
传递函数
(t)
1
1
t
eT
T
(t 0)
1
1(t)
S
t
1e T t 0
1
t
1
t
TS 1
S2
t T Te T t 0
1 t2
1
1
t2
Tt

T
2 (1
2.能熟练运用劳斯稳定性判据判断系统的稳定性
3.正确理解对控制信号和干扰作用的稳态误差定义， 能熟练应用静态误差系数法计算稳态误差。

1 h()
0.9 h()
td
0.5 h()
td
0.1 h()
0 tr tp
ts
单位阶跃响应曲线
响延应迟曲时线间第t一d ：次
达到稳态值的一 半所需的时间。
0.02或 0.05上升时间 tr :
响应曲线从稳态值 的 10%上升到 9t 0%，所需的时间。
峰值时间 t p :响应曲
线达到超调量的第一个 峰值所需要的时间。
s2 = -n - n 2 -1 = -1/ T2
R(s)
22 nn
ss((ss 22nn))
C(s)
29
二阶系统的传递函数
开环传递函数：
G(s) =
n2
s(s 2n )
闭环传递函数：
C(s) R(s)
=
s2
n2 2ns
n2
30
二阶系统的特征方程为
s2 2ns n2 = 0
解方程求得特征根：
s1,2 = -ns n 2 -1
s1,s2完全取决于 ，n两个参数。
h(tp)于终值之差的 百分比，即
单位阶跃响应曲线
tr 或t p 评价系统的响应速度；
% = h(tp ) - h() 100%
h()
t s 同时反映响应速度和阻尼程度的综合性指标。
% 评价系统的阻尼程度或振荡最大峰值。
17
注意事项：
%, ts及ess三项指标是针对阶跃响应
而言的，对于非阶跃输入，则只有
=
t
- T(1-
-1t
eT
)
=
t
-
T
-1t
Te T
因为
-1t
e(t) = r(t) - c(t) = T (1- e T )

第三章时域分析刘健副教授liujian@课件下载地址：课件下载地址voicesp2013@/voicesp123456北京科技大学3.1 语音分析方法概述语音分析是语音合成及语音识别的基础。

短时分析技术——贯穿语音分析全过程语音分析的三种方法：（1）时域分析法——时域波形图。

（2）频域分析法——频谱图。

（2）频域分析法频谱图（3）语谱分析法——语谱图。

（1）时域分析法语音的时域分析采用时域波形图。

坐是，纵坐是。

横坐标是时间，纵坐标是幅值。

（2）频域分析法频域分析包含：语音信号的频谱、功率包含信的率谱、倒频谱、频谱包络、短时间谱等。

常用的频域分析方法有：a带通滤波器组法a.带通滤波器组法。

b.傅里叶变换法。

c.线性预测法等。

（3）语谱分析法语谱分析法是另种用于语音分析的有效方语谱分析法是另一种用于语音分析的有效方法。

语谱分析法始于20世纪40年代，当时研制成功语谱仪，能生成语谱图。

语谱图可以在二维（时间及频率）图上表示音强的关系，提供了有关不同时间不同频率的相对音强的有价值的信息。

对音强的有价值的信息3.2 语音的时域分析三种常用的时域分析方法：三种常用的时域分析方法（1）过零分析（2）幅度分析/能量分析（3）相关分析3.2 语音信号数字化－采样量化语音信号数字化采样量化采样：一个数字信号取样之后，变成离散时间信号，接下来就是要用数字方式来表示这个离散时间信号上的每个取样值的每个取样值。

量化：一个电位波形会有固定的电压范围，一个取样值可以是在此电压范围内的任何电位。

如果只能用固值可以是在此电压范围内的任何电位如果只能用固定数目的位来表示这些取样值，那么这些二进数字就只能代表固定的几个电位值，这个转换就是量化只能代表固定的几个电位值这个转换就是量化(quantization)，而转换之后只允许存在的几个电位值(quantization level)就是量化阶数(quantization level)。