5四边形变身术

五阶魔方还原教学教程五阶魔方是一种非常有挑战性的立体拼图，它有着很高的难度和复杂度。

在还原五阶魔方之前，我们需要明确一些基本概念和技巧。

在本篇教程中，我将详细介绍五阶魔方的还原方法。

1.基础认识五阶魔方是由五个边长为5的小正方体组成，每个小正方体有6个面。

这些小正方体通过中心轴连接在一起，并且可以沿着各个轴旋转。

2.记号法为了方便记忆和指导操作，我们使用下列记号法：F-前面B-后面U-顶面D-底面L-左面R-右面3.拼图步骤还原五阶魔方可以分为以下几个步骤：-第一步，还原中心块。

-第二步，还原边块。

-第三步，还原角块。

-第四步，还原顶角和顶层。

-第五步，精确还原角块和边块。

-第六步，最后的调整和形状调整。

4.还原中心块首先，我们需要确定每个中心块的正确位置，然后将其还原至正确的位置。

由于中心块的位置是固定的，所以只需要移动其他小方块即可。

这一步是相对简单的，可以通过观察和实践来完成，不需要特别的技巧。

5.还原边块还原边块的方法与还原三阶魔方类似，但比较复杂。

首先，我们需要找到一个边块的位置，并将其他边块置于正确的位置。

然后，按照特定的算法实施边块的交换。

这一步需要一些算法和技巧，需要仔细学习和练习。

6.还原角块还原角块的方法与还原三阶魔方类似，但更加复杂。

同样，我们需要找到一个角块的位置，并将其他角块置于正确的位置。

然后，按照特定的算法实施角块的交换。

这一步需要一些算法和技巧，需要仔细学习和练习。

7.还原顶角和顶层在这一步中，我们需要将上面两层的顶角归位，并将顶层还原至正确位置。

这一步需要一些特殊的算法和技巧，需要慢慢琢磨和掌握。

练习这一步可能需要花费一些时间和耐心。

8.精确还原角块和边块在这一步中，我们需要将剩下的角块和边块归位，以完成整个五阶魔方的还原。

这一步可能是整个还原过程中最困难的一步，需要非常熟练的技巧和算法。

9.最后的调整和形状调整当所有的块都归位时，我们需要进行最后的调整和形状调整，以确保五阶魔方恢复到完美的状态。

霍格维茨中级变形术指南《霍格维茨中级变形术指南》嘿，新手朋友！今天我来给你讲讲霍格维茨的中级变形术。

首先呢，基本注意事项咱得清楚。

变形术可不是闹着玩的，你得集中精力，这就好比你想把一团乱麻理顺，必须得全神贯注才行。

我一开始学的时候，就总是走神，觉得变形术就是挥挥魔杖的事儿，结果啥都变不成功。

记住了，集中精力是变形术的基础，这一点很关键！实用建议来啦。

在做变形之前，你得好好观察你要变形的对象或者想着你想要变成的模样。

就像是画画儿，你得心里先有个谱儿。

比如说你要把一只老鼠变成一个杯子，那你就得把老鼠的每个细节都记在脑袋里，耳朵、尾巴咋处理都得想好。

这里有个诀窍，你可以在脑海里先构建一个完整的画面。

容易忽视的点呢？很多人不重视自己的魔杖挥动轨迹，其实这也很重要。

乱画一通是不行的，每一种变形都有对应的大致魔杖轨迹，像把一根羽毛变成一把扇子，魔杖可能就是要轻轻向右上方挑起再画一道弧线这样。

你要是不按照规律来，很可能就把羽毛变成了一团糟。

特殊情况也有啊。

有时候环境因素会影响变形术。

我就遇到过一次，在一个充满魔力干扰的房间里，要把一个凳子变成马匹，费了好大劲儿。

所以如果可以，尽量选择一个相对稳定、魔力纯净的环境来练习。

对了，还有一点很重要，变形术也要遵循魔法生物保护法等相关魔法规则哦。

可不能随便把一个重要的魔法生物变成个家具玩儿。

那总结一下要点，集中精力、认真观察、掌握魔杖轨迹、关注环境以及遵守魔法规则。

中级变形术不容易，但只要你多多练习，多想多做，肯定能成功的。

比如说我后来经过不断努力，能轻松把各种简单物件相互变形，就是遵从了这些要点。

加油呀，朋友！。

百变魔方教程
百变魔方是一款经典的智力拼图游戏，由6个面组成，每个面由9个小方块组成。

玩家需要通过转动魔方的六个面，使得每个面都是同一种颜色或图案。

1. 先将魔方的每一个面都转成同一种颜色或图案，这样可以更容易判断和操作。

2. 观察魔方，找出一个面作为起始面。

可以选择任意一个面作为起始面。

3. 着重处理起始面的四个角落。

先将四个角块都找出来。

4. 选择一个角块作为参考点，将这个角块转到正确位置。

5. 接下来处理起始面的四个边块。

同样选择一个边块作为参考点，将这个边块转到正确位置。

6. 完成起始面后，处理其它面。

同样，先解决角块，然后是边块。

注意事项：
- 每个转动都要准确无误，以免错乱其他已经恢复正常的区域。

- 操作时要保持平稳的力度，避免太过用力导致整个魔方脱落
和损坏。

百变魔方的还原需要一定的时间和耐心，初学者可以先通过一
些简单的教程和指南练习，逐渐掌握技巧和思路。

熟练后，可以尝试解决更复杂的魔方问题，挑战自己的智力和反应能力。

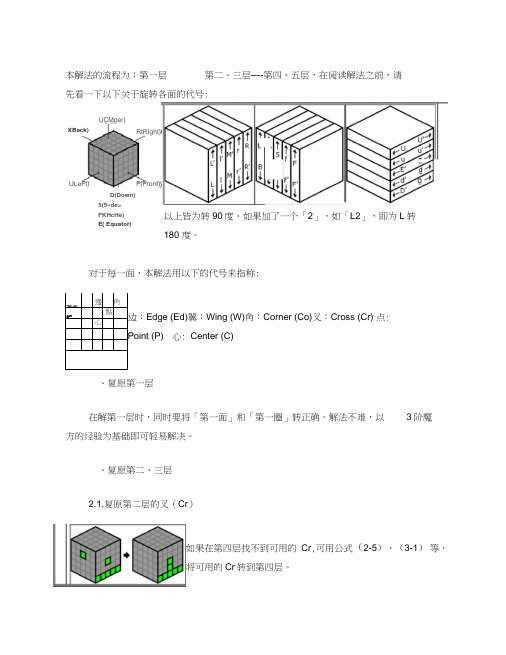
180 度。

对于每一面，本解法用以下的代号来指称: 边：Edge (Ed)翼：Wing (W)角：Corner (Co)叉：Cross (Cr) 点: Point (P) 心: Center (C) 、复原第一层在解第一层时，同时要将「第一面」和「第一圈」转正确。

解法不难，以3阶魔方的经验为基础即可轻易解决。

、复原第二、三层2.1.复原第二层的叉（Cr ）如果在第四层找不到可用的 Cr ,可用公式（2-5）、（3-1） 等，将可用的Cr 转到第四层。

本解法的流程为：第一层 第二、三层----第四、五层，在阅读解法之前，请 先看一下以下关于旋转各面的代号: XBack) ULeFt) F(Front) 以上皆为转90度。

如果加了一个「2」，如「L2」，即为L 转D(Down) 5(5»de> FKHcHe)E( Equator) UCMper) RtRIght) d D r 邊 角 r點心本步骤的目标为转成第五层5x5的十字。

这个步骤只需要一个公式，而可能会有下图中任一小图的情况。

公式与（3-1）类似，只是视之为3阶魔方I。

F' U F R公式3-2——R'U'33第五层的角（Co）的位置在本步骤中，先不要管第五层四个角的方向，以本文为例即不要管蓝色那面是否在顶面，只要管四个角所属的小方块是否在正确的位置即可。

公式3-3----L R' U' R U L' U' R' U R 公式3-4----R' L U L' U' R U L U' L'其它情况可用公式（3-3）和（3-4）的组合来解34第五层的角（C Q）的方向公式3-5----R' U' R U' R' U2 R U2 公式3-6----R U R' U R U2 R' U2其它情况可用公式（3-5）和（3-6）的组合来解3.5.第五层的边（Ed）的位置公式3-7----(3- 5) —U' —(3-6) —U 公式3-8----(3- 6) —(3-5) —U' 其它情况可用公式（3-7）和（3-8）的组合来解3.6.复原第四、五层的翼（W）优先将第五层的W转好，然后再转第四层的W（因为第五层有8个而第四层只有4个W。

神奇的形魔术通过形魔术表演展示形的奇妙变化形魔术是一种令人叹为观止的表演艺术，通过巧妙的手法和障眼法使物体的形态发生奇妙的变化。

无论是舞台上的大型表演还是身边的小道具，形魔术带给观众们无尽的惊叹与喜悦。

本文将介绍一些常见的形魔术表演以及其中的创意因素。

一、手绢变鸟手绢变鸟是最经典也最受欢迎的形魔术之一。

魔术师首先展示一块普通的手绢，然后在观众的注视下迅速将其放入手掌之中。

随后，魔术师突然打开手掌，手绢却变成了一只活蹦乱跳的小鸟！这种形魔术让观众们惊叹不已，他们难以理解手绢是如何变成鸟的。

在这个表演中，创意和技巧起着关键的作用。

魔术师利用手掌中的道具，通过巧妙的手法将手绢变成鸟。

观众们在关注魔术师的动作时，很难察觉到其中的秘密。

此外，魔术师还需要通过自信，流利的动作和幽默感来吸引观众的注意力，使他们更好地享受这一视觉盛宴。

二、变戏法的箱子变戏法的箱子是另一种经典的形魔术表演。

在这个魔术中，魔术师会进入一只普通的箱子，随后将箱子的门紧紧关闭。

观众们觉得魔术师已经被困在了箱子里，然而当箱子的门再度打开时，魔术师竟然变成了另一个人，或者完全消失了！这种表演往往让观众们目瞪口呆，他们纷纷议论着魔术师是如何做到的。

变戏法的箱子表演需要魔术师有极高的技巧和熟练的准备工作。

箱子内部配备了隐蔽的通道或者折叠的空间，魔术师通过这些特殊设计来实现自己的变化或者消失。

观众们在没有发现这些细节的情况下，很难解释箱子里发生的神奇变化。

同时，魔术师还需要把握好节奏，通过惊悚的氛围和扣人心弦的音乐来增强观众的感官体验。

三、扑克牌变换扑克牌变换是一种极具技巧性的形魔术表演。

魔术师通过快速的手势和变戏法的道具使扑克牌在观众的眼前发生奇妙的变化。

他们可以将一张扑克牌变成另一张，或者通过变换顺序和排列使观众难以分辨各张扑克牌的变化。

这种形魔术表演需要魔术师具备高超的手法和洞察力。

魔术师必须熟练掌握扑克牌的各种变化和手法，并能在短时间内完成连续的操作。

第1章走进数学世界•§1.1 从实际问题到方程•§1。

2让我们来做数学•单元测试•同步练习•本章综合第2章有理数• 2.1正数和负数•2。

2数轴•2。

3相反数• 2.4绝对值•2。

5有理数的大小比较•2。

6有理数的加法•2。

7有理数的减法• 2.8有理数加减混合运算•2。

9有理数的乘法•2．10 有理数的除法•2．11 有理数的乘方•2．12 科学记数法•2．13 有理数的混合运算•2．14 近似数和有效数字•2．15 用计算器进行数的简单运算•单元测试•同步练习•本章综合第3章整式的加减•3．1 列代数式•3．2 代数式的值•3．3 整式•3．4 整式的加减•单元测试•同步练习•本章综合第4章图形的初步认识•4．1生活中的立体图形•4．2 画立体图形•4．3立体图形的展开图•4．4平面图形•4．5最基本的图形—-点和线•4．6角•4．7相交线•4．8平行线•单元测试•同步练习•本章综合第5章数据的收集与表示•5。

1 数据的收集•5．2数据的表示•单元测试•同步练习•本章综合第6章一元一次方程• 6.1 从实际问题到方程• 6.2 解一元一次方程• 6.3 实践与探索•单元测试•同步练习•本章综合第7章二元一次方程组•7。

1 二元一次方程组和它的解•7.2 二元一次方程组和它的解法•7。

3 实践与探索•单元测试•同步练习•本章综合第8章一元一次不等式•8.1认识不等式•8。

2解一元一次不等式•8。

3一元一次不等式组•单元测试•同步练习•本章综合第9章多边形•8。

1 瓷砖的铺设•9.1 三角形•9.2 多边形的内角和和外角和•9。

3 用正多边形拼地板•单元测试•同步练习•本章综合第10章轴对称•10.1 生活中的轴对称•10.2 轴对称的认识•10。

3等腰三角形•单元测试•同步练习•本章综合第11章体验不确定现象•11。

1可能还是确定•11.2机会的均等与不等•11.3在反复实验中观察不确定现象•单元测试•同步练习•本章综合(老)第10章统计的初步认识•全章教案•10.1 统计的意义•10。

五魔方还原教程
魔方是一种训练智力和手眼协调能力的经典玩具，以下是五魔方的还原教程：
第一步：还原顶面十字
首先，选择一个颜色作为顶层的中心块，将其他颜色的中心块对准各自的面。

接下来，寻找与顶层中心块相邻的四个边块，使魔方出现一个十字形状。

调整边块的位置，直到得到正确的十字形状。

第二步：还原顶层角块
找到顶层角块，并确认每个角块应该归位的位置。

将角块移到正确的位置，并按照顺时针或逆时针的方式旋转角块，直到顶层角块归位。

第三步：还原中层边块
找到中间层的边块，并将它们移动到正确的位置。

可能需要通过临时移动和旋转顶层块来解决中层边块的位置问题。

第四步：还原底层角块
找出底层的角块，并将其放置到正确的位置。

可能会破坏之前还原的层，但不要担心，后续将重新调整。

第五步：还原底层边块
最后一步是还原底层的边块。

将边块移到正确的位置，并使用旋转的方法解决底层边块的排列问题。

完成以上五个步骤后，你将成功还原五魔方！记住，这需要一些时间和练习，但相信坚持下去，你一定可以轻松还原魔方。

五魔方复原方法（彩图版）只要学会三阶魔方复原，仔细琢磨一下，即可学会五魔方的复原。

（文中所讲某色片是以五角星中心颜色，和三阶魔方心块一样）一、第一层：１、五角星：像三阶的十字一样，同样它们所对应的另一色要与所在面的中心块颜色一致。

２、五个角：将五角星放在顶层，找到有顶层颜色的角块放在目标位置的下方，并使顶层颜色位于侧面，另一颜色与所在那一面的颜色一致，向下转动顶层颜色所在的那个面，再或左或右转动下边的面使目标块到达刚才的位置，再向上转回先前下来的面。

目标：白棕深粉块棕色片逆时一下深兰色片逆时一下棕色片顺时一下二、第二层是指第一层五个角块下边的五个棱块。

将目标块放在目标位置下边的位置，并要使在当前面的颜色一致，向上转动目标位置对面的面2下，转动顶层使刚才转上去的棱到达前面来，转动当前面使目标块到达目标位置，再将顶层转回去，再将那个侧面向下转2下转回去。

目标：绿粉块深绿片顺时两下白色片顺时一下绿色片顺时两下白色片逆时一下深绿片逆时两下三、第三层指第二层下边的五个角块。

使目标块的一个颜色与某侧面颜色一致，转动这个面若干次，即可。

目标：绿黄深绿块黄色片顺时两下四、第四层指第三层五个角块两侧的十个棱块。

使目标块到达底层目标位置所在面，为当前面。

１、如果棱块在当前面的颜色与当前面颜色一致，则向上转动目标位置对面那个侧面，再向上转动目标位置与对面侧面中间的那个侧面，然后转动当前面2下，使目标块到达目标位置，再向下转回目标位置与对面侧面中间的那个侧面，再向下转回目标位置对面那个侧面。

目标：红棕块浅棕色片顺时一下粉色片顺时一下红色片顺时两下粉色片逆时一下浅棕色片逆时一下２、如果棱块在当前面的颜色与当前面颜色不一致，则先转动底层将目标块移到目标位置对面的那个侧面，再向上转动这个侧面，再向上转动目标位置与对面侧面中间的那个侧面，然后转动当前面2下，使目标块到达目标位置，再向下转回目标位置与对面侧面中间的那个侧面，再向下转回目标位置对面那个侧面。

五阶魔方还原法—降阶法一、认识五阶魔方五阶魔方（Professor Cube）共有54个面中心块，36个棱块和8个角块，普通六色纯色五阶魔方变化总数为(8!*3^7*12!*2^10*24!*24!*24!)/((4!)^12)=282,870,942,277,741,856,536,180,333,107,150,328,293,127,731,985,672,134,721,536,000,000,000,000,000≈2.8*10^74种。

下图就是一个五阶魔方。

二、降阶法降阶法，顾名思义就是把魔方的阶数降下来。

大家见得最多的魔方就是三阶魔方，一般的降阶法也是指的将高阶魔方降成三阶魔方来解。

降阶法解高阶魔方的思路是：首先还原高阶魔方的面心，然后将各条棱对好，此时的魔方就基本变成了一个三阶魔方，然后再按照三阶魔方的解法复原即可。

之所以说“基本”，是因为对于偶数阶魔方，有可能还需要一些特殊的处理，而奇数阶的魔方就肯定能直接还原。

在最后按照三阶魔方还原的过程中，只能也只需要转动表面一层（偶数阶除外）。

三、指令公式系统介绍在下文中，我将使用如下的指令系统F——前面R——右面U——上面D——下面B——后面L左面字母表示对应的表面顺时针转动90度，在后面加'表示逆时针转动90度，加2表示转动180度。

在字母前面加T表示转动两层，加M表示转动第二层，加M1表示转动中间层。

如F R' U2 TB M1D' MF' TU2等。

MR＝TR R'对于五阶魔方来说，我们第一步来完成六面中心块的复原，第二步完成12个棱块的复原，第三步我们就完全可以用三阶的公式来完成复原了四、各面中心块的还原形成中心块，变成型如：在我们完成中心块的时候，前面我们完全可以不用公式，自己根据玩魔方的经验，完全可以完成4面中心块的复原，只是在完成最后两面中心块的过程中为了保持已经完成的四面的中心块不被破坏，处理用的步骤稍微复杂一点，下面介绍的就是两个这样的公式，其实也就是一点点小小的技巧，很多朋友估计不看公式也是这样来完成的，在此，我们仅仅是提供一种思路，其中的一些技巧，大家可活学活用。