水平地震作用的振型分解反应谱法

振型分解反应谱法振型分解反应谱法是用来计算多自由度体系地震作用的一种方法。

该法是利用单自由度体系的加速度设计反应谱和振型分解的原理，求解各阶振型对应的等效地震作用，然后按照一定的组合原则对各阶振型的地震作用效应进行组合，从而得到多自由度体系的地震作用效应。

振型分解反应谱法一般可考虑为计算两种类型的地震作用：不考虑扭转影响的水平地震作用和考虑平扭藕联效应的地震作用。

适用条件〔1〕高度不超过40米，以剪切变形为主且质量和刚度沿高度分布比较均匀的结构，以及近似于单质点体系的结构，可采用底部剪力法计算。

〔此为底部剪力法的适用范围〕〔2〕除上述结构以外的建筑结构，宜采用“振型分解反应谱法”。

〔3〕特别不规则的建筑、甲类建筑和标准规定的高层建筑，应采用时程分析法进行补充计算。

刚重比刚重比是指结构的侧向刚度和重力荷载设计值之比，是影响重力二阶效应的主要参数刚重比=Di*Hi/GiDi-第i楼层的弹性等效刚度，可取该层剪力与层间位移的比值Hi-第i楼层层高Gi-第i楼层重力荷载设计值刚重比与结构的侧移刚度成正比关系；周期比的调整将导致结构侧移刚度的变化，从而影响到刚重比。

因此调整周期比时应注意，当某主轴方向的刚重比小于或接近标准限值时，应采用加强刚度的方法；当某主轴方向刚重比大于标准限值较多时，可采用削弱刚度的方法。

同样，对刚重比的调整也可能影响周期比。

特别是当结构的周期比接近标准限值时，应采用加强结构外围刚度的方法标准上限主要用于确定重力荷载在水平作用位移效应引起的二阶效应是否可以忽略不计。

见高规5.4.1和5.4.2及相应的条文说明。

刚重比不满足标准上限要求，说明重力二阶效应的影响较大，应该予以考虑。

标准下限主要是控制重力荷载在水平作用位移效应引起的二阶效应不致过大，防止结构的失稳倒塌。

见高规5.4.4及相应的条文说明。

刚重比不满足标准下限要求，说明结构的刚度相对于重力荷载过小。

但刚重比过分大，则说明结构的经济技术指标较差，宜适当减少墙、柱等竖向构件的截面面积。

掌握地震动的基本特性，结构地震响应特性，反应谱，钢筋混凝土结构、钢结构、砌体结构和桥梁结构的抗震验算和构造措施，隔震减震的基本原理等。

掌握排架结构简化为单质点体系时，多遇地震水平地震作用标准值的计算（例题3.1）钢筋混凝土框架简化成多质点体系时，用振型分解反应谱法计算该框架在多遇地震下的层间地震剪力，以及内力图。

（例题3.3）多层钢筋混凝土框架结构，用底部剪力法计算其在多遇地震作用下各质点上的水平地震作用。

（例题3.7）一、填空题1、构造地震为由于地壳构造运动造成地下岩层断裂或错动引起的地面振动。

2、建筑的场地类别，可根据土层等效剪切波速和场地覆盖层厚度划分为四类。

3、《抗震规范》将50年内超越概率为 10% 的烈度值称为基本地震烈度，超越概率为 63.2% 的烈度值称为多遇地震烈度。

4、丙类建筑房屋应根据抗震设防烈度，结构类型和房屋高度采用不同的抗震等级。

5、柱的轴压比n定义为 n=N/fc Ac（柱组合后的轴压力设计值与柱的全截面面积和混凝土抗压强度设计值乘积之比）6、震源在地表的投影位置称为震中，震源到地面的垂直距离称为震源深度。

7、表征地震动特性的要素有三，分别为振幅、频谱和持时。

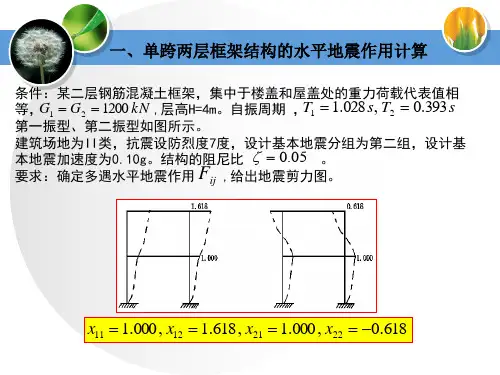
8、某二层钢筋混凝土框架结构，集中于楼盖和屋盖处的重力荷载代表值相等G 1=G2=1200kN,第一振型φ12/φ11=1.618/1;第二振型φ22/φ21=-0.618/1。

则第一振型的振型参与系数j= 0、724 。

9、多层砌体房屋楼层地震剪力在同一层各墙体间的分配主要取决于楼盖的水平刚度（楼盖类型）和各墙体的侧移刚度及负荷面积。

10、建筑平面形状复杂将加重建筑物震害的原因为扭转效应、应力集中。

11、在多层砌体房屋计算简图中，当基础埋置较深且无地下室时，结构底层层高一般取至 室外地面以下500mm 处 。

12、某一场地土的覆盖层厚度为80米，场地土的等效剪切波速为200m/s,则该场地的场地土类别为 Ⅲ类场地 （中软土） 。

简述振型分解反应谱法求地震作用的步骤振型分解反应谱法是一种常用的求解地震作用的方法。

其基本思想是将结构的振型分解成若干个单自由度系统，并在每个单自由度系统上进行分析，最后将分析结果合成得到整个结构的反应谱。

具体步骤如下：
1. 确定结构的振型
通过结构的模态分析，得到结构的振型及对应的振动周期和阻尼比。

2. 将振型分解为单自由度系统
根据振型的特点，将其分解为若干个单自由度系统，并确定每个单自由度系统的振动周期和阻尼比。

3. 计算单自由度系统的反应谱
在每个单自由度系统上，按照地震加速度谱和单自由度系统的特性进行计算，得到该单自由度系统的反应谱。

4. 合成结构的反应谱
将各个单自由度系统的反应谱按照一定的规则进行合成，得到整个结构在不同周期下的反应谱。

5. 分析反应谱
根据结构的设计要求和反应谱的分析结果，确定结构在地震作用下的最大位移、最大加速度等参数，以便进行结构的设计和验算。

总之，振型分解反应谱法是一种简单有效的求解地震作用的方法，但其结果的精度受到结构的振型分解精度等因素的影响，需要结合实
际情况进行综合分析。

简答题１、简述两阶段三水准抗震设计方法。

答：我国《建筑抗震设计规范》（GB50011-2001）规定：进行抗震设计的建筑，其抗震设防目标是：当遭受低于本地区抗震设防烈度的多遇地震影响时，一般不受损坏或不需修理可继续使用，当遭受相当于本地区抗震设防烈度的地震影响时，可能损坏，经一般修理或不需修理仍可继续使用，当遭受高于本地区抗震设防烈度预估的罕遇地震影响时，不致倒塌或发生危及生命的严重破坏。

具体为两阶段三水准抗震设计方法：第一阶段是在方案布置符合抗震设计原则的前提下，按与基本烈度相对应的众值烈度的地震动参数，用弹性反应谱求得结构在弹性状态下的地震作用效应，然后与其他荷载效应组合，并对结构构件进行承载力验算和变形验算，保证第一水准下必要的承载力可靠度，满足第二水准烈度的设防要求（损坏可修），通过概念设计和构造措施来满足第三水准的设防要求；对大多数结构，一般可只进行第一阶段的设计。

对于少数结构，如有特殊要求的建筑，还要进行第二阶段设计，即按与基本烈度相对应的罕遇烈度的地震动参数进行结构弹塑性层间变形验算，以保证其满足第三水准的设防要求。

2、简述确定水平地震作用的振型分解反应谱法的主要步骤。

（1）计算多自由度结构的自振周期及相应振型；（2）求出对应于每一振型的最大地震作用（同一振型中各质点地震作用将同时达到最大值）；（3）求出每一振型相应的地震作用效应；（4）将这些效应进行组合，以求得结构的地震作用效应。

3、简述抗震设防烈度如何取值。

答：一般情况下，抗震设防烈度可采用中国地震动参数区划图的地震基本烈度(或与本规范设计基本地震加速度值对应的烈度值)。

对已编制抗震设防区划的城市，可按批准的抗震设防烈度或设计地震动参数进行抗震设防。

4、简述框架节点抗震设计的基本原则。

节点的承载力不应低于其连接构件的承载力；多遇地震时节点应在弹性范围内工作；罕遇地震时节点承载力的降低不得危及竖向荷载的传递；梁柱纵筋在节点区内应有可靠的锚固；节点配筋不应使施工过分困难。

振型分解反应谱法振型分解反应谱法是用来计算多自由度体系地震作用的一种方法。

该法是利用单自由度体系的加速度设计反应谱和振型分解的原理，求解各阶振型对应的等效地震作用，然后按照一定的组合原则对各阶振型的地震作用效应进行组合，从而得到多自由度体系的地震作用效应。

振型分解反应谱法一般可考虑为计算两种类型的地震作用：不考虑扭转影响的水平地震作用和考虑平扭藕联效应的地震作用。

适用条件（1）高度不超过40米，以剪切变形为主且质量和刚度沿高度分布比较均匀的结构，以及近似于单质点体系的结构，可采用底部剪力法计算。

（此为底部剪力法的适用范围）（2）除上述结构以外的建筑结构，宜采用“振型分解反应谱法”。

（3）特别不规则的建筑、甲类建筑和规范规定的高层建筑，应采用时程分析法进行补充计算。

刚重比刚重比是指结构的侧向刚度和重力荷载设计值之比，是影响重力二阶效应的主要参数刚重比=Di*Hi/GiDi-第i楼层的弹性等效刚度，可取该层剪力与层间位移的比值Hi-第i楼层层高Gi-第i楼层重力荷载设计值刚重比与结构的侧移刚度成正比关系；周期比的调整将导致结构侧移刚度的变化，从而影响到刚重比。

因此调整周期比时应注意，当某主轴方向的刚重比小于或接近规范限值时，应采用加强刚度的方法；当某主轴方向刚重比大于规范限值较多时，可采用削弱刚度的方法。

同样，对刚重比的调整也可能影响周期比。

特别是当结构的周期比接近规范限值时，应采用加强结构外围刚度的方法规范上限主要用于确定重力荷载在水平作用位移效应引起的二阶效应是否可以忽略不计。

见高规5.4.1和5.4.2及相应的条文说明。

刚重比不满足规范上限要求，说明重力二阶效应的影响较大，应该予以考虑。

规范下限主要是控制重力荷载在水平作用位移效应引起的二阶效应不致过大，避免结构的失稳倒塌。

见高规5.4.4及相应的条文说明。

刚重比不满足规范下限要求，说明结构的刚度相对于重力荷载过小。

但刚重比过分大，则说明结构的经济技术指标较差，宜适当减少墙、柱等竖向构件的截面面积。

六、 计算题1、某两层钢筋混凝土框架，集中于楼盖和屋盖处的重力荷载代表值相等kN 120021==G G ，每层层高皆为4.0m ，各层的层间刚度相同m /kN 863021=∑=∑D D ；Ⅱ类场地，设防烈度为7度，设计基本地震加速度为0.10g ，设计分组为第二组，结构的阻尼比为05.0=ζ。

（1）求结构的自振频率和振型，并验证其主振型的正交性（2）试用振型分解反应谱法计算框架的楼层地震剪力解1）：（1）计算刚度矩阵m kN k k k /17260286302111=⨯=+=m kN k k k /863022112-=-==m kN k k /8630222==（2）求自振频率])(4)()[(21211222112121122211122212122,1k k k k m m k m k m k m k m m m --++= ω ])8630(863017260[(1201204)172601208630120()172601208630120[(1201202122--⨯⨯⨯-⨯+⨯⨯+⨯⨯⨯=28.188/47.27=s r a d /24.51=ω s rad /72.132=ω（3）求主振型当s r a d /24.51=ω 1618.186301726024.5120212112111112=--⨯=-=k k m X X ω 当s rad /72.132=ω1618.086301726072.13120212112212122-=--⨯=-=k k m X X ω （4）验证主振型的正交性质量矩阵的正交性0618.0000.112000120618.1000.1}]{[}{21=⎭⎬⎫⎩⎨⎧-⎥⎦⎤⎢⎣⎡⎭⎬⎫⎩⎨⎧=T T X m X 刚度矩阵的正交性 0618.0000.186308630863017260618.1000.1}]{[}{21=⎭⎬⎫⎩⎨⎧-⎥⎦⎤⎢⎣⎡--⎭⎬⎫⎩⎨⎧=T T X k X 解2）：由表3.2查得：Ⅱ类场地，第二组，T g =0.40s由表3.3查得：7度多遇地震08.0max=α 第一自振周期g g T T T T 5s,200.12111<<==ωπ 第二自振周期g g T T T T 5s,458.02122<<==ωπ （1）相应于第一振型自振周期1T 的地震影响系数：030.008.0200.140.09.0max 9.011=⨯⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=ααT T g第一振型参与系数 724.0618.11200000.11200618.11200000.11200222121111=⨯+⨯⨯+⨯==∑∑==i i i n i i i m m φφγ 于是：kN 06.261200000.1724.0030.01111111=⨯⨯⨯==G F φγαkN 17.421200618.1724.0030.02121112=⨯⨯⨯==G F φγα第一振型的层间剪力：kN 17.421212==F VkN 23.68121111=+=F F V（2）相应于第二振型自振周期2T 的地震影响系数： 071.008.0458.040.09.0max 9.022=⨯⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=ααT T g第二振型参与系数 276.0)618.0(1200000.11200)618.0(1200000.11200222122122=-⨯+⨯-⨯+⨯==∑∑==i i i n i i i m m φφγ 于是：kN 52.231200000.1276.0071.01212221=⨯⨯⨯==G F φγαkN 53.141200)618.0(276.0071.02222222-=⨯-⨯⨯==G F φγα第二振型的层间剪力：kN 53.142222-==F VkN 99.8222121=+=F F V（3）由SRSS 法，计算各楼层地震剪力： kN 60.44)53.14(17.422222222=-+==∑=j j V VkN 821.6899.823.682222211=+==∑=j j VV2、某两层钢筋混凝土框架，集中于楼盖和屋盖处的重力荷载代表值相等kN 120021==G G ，每层层高皆为4.0m ，框架的自振周期s 028.11=T ；各层的层间刚度相同m /kN 863021=∑=∑D D ；Ⅱ类场地，7度第二组（)08.0 s,40.0max ==αg T ，结构的阻尼比为05.0=ζ，试按底部剪力法计算框架的楼层地震剪力，并验算弹性层间位移是否满足要求（[]450/1=e θ）。

振型分解反应谱法适用条件振型分解反应谱法是结构抗震分析中常用的一种方法，适用于计算结构在地震作用下的响应。

其基本思想是将结构的振型与地震的加速度谱进行分解，并根据结构的特征频率和阻尼比，计算出结构在各个频率下的响应加速度谱。

本文将从振型分解反应谱法的原理、适用条件以及优点等方面进行阐述。

首先，需要明确振型分解反应谱法的基本原理。

振型分解反应谱法是基于结构的振型及地震的加速度谱进行分解，因此对于结构的振型特性要有充分的了解。

一般情况下，可以通过模态分析或实测得到结构的振型以及主要模态参数。

而地震的加速度谱可通过地震地点的加速度记录或根据地震地点的设计地震参数进行计算。

在得到结构的振型和地震的加速度谱后，可以对结构的动力特性进行分析，进而计算出结构在不同频率下的响应加速度谱。

振型分解反应谱法适用于计算结构在地震作用下的响应，其适用条件如下：1.结构线性静力弹性响应：振型分解反应谱法是基于线性弹性理论进行分析的，因此适用于线性静力弹性响应的结构。

对于非线性结构，需要进行合理的线性化处理才能应用该方法。

2.单自由度系统或多自由度系统：振型分解反应谱法适用于单自由度系统和多自由度系统。

对于单自由度系统，可以直接进行分析；对于多自由度系统，需要将结构的多个振型进行叠加计算，得到整个结构的响应。

3.结构模态参数已知：振型分解反应谱法需要结构的振型特性，包括特征频率和阻尼比。

因此需要事先通过模态分析或实测等方法获得结构的振型模态参数。

4.地震加速度谱已知：振型分解反应谱法需要地震的加速度谱，以描述地震动的频率特性。

可以通过地震地点的实测记录或根据设计地震参数进行计算。

5.结构的线性动力特性：振型分解反应谱法适用于具有线性动力特性的结构。

如果结构的振型特征存在非线性特性，需要进行合理的线性化处理才能使用该方法。

振型分解反应谱法具有以下优点：1.能够考虑结构的频率特性：振型分解反应谱法通过分解结构的振型以及地震的加速度谱，能够充分考虑结构的频率特性。

1、《抗震规范》给出的设计反应谱中，当结构自振周期在0.1s~Tg之间时，谱曲线为（A ）A．水平直线 B.斜直线 C.抛物线 D.指数曲线2、实际地震烈度与下列何种因素有关？（ B ）A.建筑物类型B.离震中的距离C.行政区划D.城市大小3、规范规定不考虑扭转影响时，用什么方法进行水平地震作用效应组合的计算？（ B ）A.完全二次项组合法（CQC法）B. 平方和开平方法（SRSS法）C.杜哈米积分D. 振型分解反应谱法4、基底剪力法计算水平地震作用可用于下列何种建筑? ( C )A.40米以上的高层建筑B.自振周期T1很长(T1>4s)的高层建筑C. 垂直方向质量、刚度分布均匀的多层建筑D. 平面上质量、刚度有较大偏心的多高层建筑5、地震系数k与下列何种因素有关？( A )A.地震基本烈度B.场地卓越周期C.场地土类别D.结构基本周期6、9度区的高层住宅竖向地震作用计算时，结构等效总重力荷载G eq为（C ）A. 0.85(1.2恒载标准值G K+1.4活载标准值Q K)B. 0.85(G K+Q k)C. 0.75(G K+0.5Q K)D. 0.85(G K+0.5Q K)7、框架结构考虑填充墙刚度时,T1与水平弹性地震作用F e有何变化?( A )A.T1↓,F e↑B.T1↑,F e↑C.T1↑,F e↓D.T1↓,F e↓8、抗震设防区框架结构布置时，梁中线与柱中线之间的偏心距不宜大于（ A ）A．柱宽的1/4 B．柱宽的1/8 C．梁宽的1/4 D．梁宽的1/89、土质条件对地震反应谱的影响很大，土质越松软，加速度谱曲线表现为（ A ）A．谱曲线峰值右移B．谱曲线峰值左移C．谱曲线峰值增大D．谱曲线峰值降低10、震中距对地震反应谱的影响很大，在烈度相同的条件下，震中距越远，加速度谱曲线表现为（ A ）A．谱曲线峰值右移 B．谱曲线峰值左移C．谱曲线峰值增大 D．谱曲线峰值降低11、为保证结构“大震不倒”，要求结构具有( C )A.较大的初始刚度B.较高的截面承载能力C.较好的延性D.较小的自振周期T112、楼层屈服强度系数 沿高度分布比较均匀的结构，薄弱层的位置为（D ）A.最顶层B.中间楼层C. 第二层D. 底层13、多层砖房抗侧力墙体的楼层水平地震剪力分配 ( B )A.与楼盖刚度无关B.与楼盖刚度有关C.仅与墙体刚度有关D.仅与墙体质量有关14、场地特征周期T g与下列何种因素有关?( C )A.地震烈度B.建筑物等级C.场地覆盖层厚度D.场地大小15、关于多层砌体房屋设置构造柱的作用，下列哪句话是错误的（D ）A．可增强房屋整体性，避免开裂墙体倒塌B．可提高砌体抗变形能力C．可提高砌体的抗剪强度D．可抵抗由于地基不均匀沉降造成的破坏16、考虑内力塑性重分布，可对框架结构的梁端负弯矩进行调幅（B）A．梁端塑性调幅应对水平地震作用产生的负弯矩进行B．梁端塑性调幅应对竖向荷载作用产生的负弯矩进行C．梁端塑性调幅应对内力组合后的负弯矩进行D．梁端塑性调幅应只对竖向恒荷载作用产生的负弯矩进行17、水平地震作用标准值F ek的大小除了与质量,地震烈度,结构自振周期有关外,还与下列何种因素有关? ( B )A.场地平面尺寸B.场地特征周期C.荷载分项系数D.抗震等级18、表征地震动特性的要素有三个，下列哪项不属于地震动要素（B ）A.加速度峰值B.地震烈度C.频谱特性D.地震持时19、震级大的远震与震级小的近震对某地区产生相同的宏观烈度，则对该地区产生的地震影响是（B ）A．震级大的远震对刚性结构产生的震害大B．震级大的远震对柔性结构产生的震害大C．震级小的近震对柔性结构产生的震害大D．震级大的远震对柔性结构产生的震害小20、地震烈度主要根据下列哪些指标来评定（ C ）A．地震震源释放出的能量的大小B．地震时地面运动速度和加速度的大小C．地震时大多数房屋的震害程度、人的感觉以及其他现象D．地震时震级大小、震源深度、震中距、该地区的土质条件和地形地貌21、一般情况下，工程场地覆盖层的厚度应按地面至剪切波速大于多少的土层顶面的距离确定（ D ）A．200m/s B．300m/s C．400m/s D．500m/s22、关于地基土的液化，下列哪句话是错误的（A）A．饱和的砂土比饱和的粉土更不容易液化B．地震持续时间长，即使烈度低，也可能出现液化C．土的相对密度越大，越不容易液化D．地下水位越深，越不容易液化23、某地区设防烈度为7度，乙类建筑抗震设计应按下列要求进行设计（D ）A．地震作用和抗震措施均按8度考虑B．地震作用和抗震措施均按7度考虑C．地震作用按8度确定，抗震措施按7度采用D．地震作用按7度确定，抗震措施按8度采用24、框架柱轴压比过高会使柱产生（B ）A．大偏心受压构件B．小偏心受压构件C．剪切破坏D．扭转破坏25、钢筋混凝土丙类建筑房屋的抗震等级应根据那些因素查表确定（B ）A．抗震设防烈度、结构类型和房屋层数B．抗震设防烈度、结构类型和房屋高度C．抗震设防烈度、场地类型和房屋层数D．抗震设防烈度、场地类型和房屋高度26、纵波、横波和面波（L波）之间的波速关系为（A ）A．V P > V S > V L B．V S > V P > V L C．V L > V P > V S D．V P > V L> V S27、位于软弱场地上,震害较重的建筑物是:（A ）A.木楼盖等柔性建筑B.单层框架结构C.单层厂房结构D.多层剪力墙结构28、强剪弱弯是指:（B ）A.抗剪承载力Vu大于抗弯承载力MuB.剪切破坏发生在弯曲破坏之后C.设计剪力大于设计弯矩D.柱剪切破坏发生在梁剪切破坏之后29、下列结构延性哪个延性在抗震设计时要求最高（D ）A.结构总体延性B.结构楼层的延性C.构件的延性D.关键杆件的延性30、强柱弱梁是指:（B ）A.柱线刚度大于梁线刚度B.柱抗弯承载力大于梁抗弯承载力C.柱抗剪承载力大于梁抗剪承载力 C.柱配筋大于梁配筋1、工程结构抗震设防的三个水准是什么？如何通过两阶段设计方法来实现？答：抗震设防的三个水准：第一水准：当遭受低于本地区抗震设防烈度的多遇地震影响时，一般不受损坏或不需修理仍可继续使用；第二水准：当遭受相当于本地区抗震设防烈度的地震影响时，可能损坏，经一般修理或不需修理仍可继续使用；第三水准：当遭受高于本地区抗震设防烈度的罕遇地震影响时，不致倒塌或发生危及生命的严重破坏。

常用的地震分析方法
国内常用的分析法都有底部剪力法，振型分解反应谱法和时程分析法。

1、底部剪力法
适用条件:对于重量和刚度沿高度分布比较均匀、高度不超过40m，并以剪切变形为主(房屋高宽比小于4时)的结构，振动时具有以下特点;(1)位移反应以基本振型为主;(2)基本振型接近直线。

基本原理:在振型分解反应谱法的基础上，针对某些建筑物的特定条件做进一步简化，而得到的一种近似计算水平地震作用的方法:将多自由度体系简化成单自由度体系，计算出结构总的地震作用(即结构底部剪力)，再将其按倒三角形原则分配到各个楼层，计算结构内力。

2、振型分解反应谱法
适用范围:除上述底部剪力法外的建筑结构。

基本原理:利用振型分解法的概念，把多自由度体系分解成若干个单自由度体系振动的组合，并利用单自由度体系的反应谱理论计算各个振型振动的地震作用，最后将各个振型计算出的地震效应按一定的规则组合起来，求出总的地震响应。

3、时程分析法
适用范围:《抗震规范》规定，重要的工程结构，例如:大跨
桥梁，特别不规则建筑、甲类建筑，高度超出规定范围的高层建筑应采用时程分析法进行补充计算。

基本原理:时程分析法是对结构物的运动微分方程直接进行逐步积分求解的一种动力分析方法。

由时程分析可得到各质点随时间变化的位移、速度和加速度动力反应，并进而可计算出构件内力的时程变化关系。

简述确定结构地震作用的振型分解反应谱法的基本原理结构地震作用是指当地震发生时，土地和建筑结构受到强烈震动的现象。

这种地震作用对建筑物的安全性、抗震等级和寿命有着重要的影响。

为了研究建筑结构的抗震性能，需要掌握结构地震作用的特点和规律。

振型分解反应谱法是一种最常用的结构地震反应计算方法之一，本文将对其基本原理进行简述。

振型分解反应谱法是一种建筑结构的动力分析方法，其原理是将结构的振动分解为一系列单自由度振动系统的组合。

这些单自由度结构可以看作是理想的固定质量、无阻尼、线性弹性振动系统，其特定振动模式称为振型。

建筑结构的复杂振动模式可以通过这些简单的振型组合表示出来，从而计算建筑结构的反应谱。

在振型分解反应谱法中，先要将建筑结构的振动模式分解为单自由度振动系统，然后对每个单自由度系统进行动力分析。

在单自由度振动系统中，结构包含一个质点及其连接着的刚性弹簧和阻尼器。

在地震激励下，质点会因惯性力而振动，其振动的形式由单自由度系统的振型所决定。

振型由结构的固有振动和阻尼比所决定。

通过计算每个单自由度系统的反应谱，可以获得结构在地震作用下的最大响应。

在振型分解反应谱计算中，每个振型被赋予一个动力增益因子。

该因子测定了该振型对于特定的频率范围内地震激励的放大效应。

动力增益因子的大小受到结构的频率和阻尼比的影响。

因此，结构频谱密度和激励频谱密度的乘积可以得到该振型的放大系数。

通过对不同振型的反应谱进行叠加，可以得到结构的总反应谱。

总反应谱代表结构的响应特性，包括其最大加速度、速度和位移。

同时，当知道入射地震波的激励谱时，可以通过反应谱计算出结构的最大位移、应力和感应力等参数。

总之，振型分解反应谱法是一种有效的结构地震反应计算方法，其基本原理是将结构振动分解为单自由度振动系统，通过计算每个单自由度系统的反应谱来获得结构的总反应谱。

利用振型分解反应谱法可以计算结构地震作用下的反应特性，为建筑结构的抗震设计和评估提供重要依据。

振型分解反应谱法公式推导过程一、振型分解反应谱法基本原理。

1. 多自由度体系的运动方程。

- 对于一个具有n个自由度的线性弹性结构体系，在地震作用下的运动方程为：M ẍ(t)+C ẋ(t)+Kx(t)= - M1ẍ_g(t)其中，M为质量矩阵（n× n阶），C为阻尼矩阵（n× n阶），K为刚度矩阵（n× n阶），ẍ(t)、ẋ(t)和x(t)分别为相对于地面的加速度、速度和位移向量（n维），ẍ_g(t)为地震地面加速度时程，1是元素全为1的列向量。

2. 振型分解。

- 假设多自由度体系的位移x(t)可以按照体系的振型φ_j（j = 1,2,·s,n）进行分解，即：x(t)=∑_j = 1^nφ_jq_j(t)其中，φ_j为第j阶振型向量（n维），q_j(t)为第j阶广义坐标（标量）。

- 将x(t)=∑_j = 1^nφ_jq_j(t)代入运动方程M ẍ(t)+C ẋ(t)+Kx(t)= - M1ẍ_g(t)，然后左乘φ_i^T（φ_i的转置向量），得到：φ_i^TM∑_j = 1^nφ̈_jq_j(t)+φ_i^TC∑_j = 1^nφ̇_jq_j(t)+φ_i^TK∑_j = 1^nφ_jq_j(t)=-φ_i^TM1ẍ_g(t)- 由于振型具有正交性，即φ_i^TMφ_j=0（i≠ j），φ_i^TKφ_j=0（i≠ j），并且对于比例阻尼C = α M+β K，也有φ_i^TCφ_j=0（i≠ j）。

- 当i = j时，定义广义质量M_j^*=φ_j^TMφ_j，广义刚度K_j^*=φ_j^TKφ_j，广义阻尼C_j^*=φ_j^TCφ_j，则对于第j阶振型，有：M_j^*q_j(t)+C_j^*q_j(t)+K_j^*q_j(t)=-φ_j^TM1ẍ_g(t)进一步化为标准形式：q_j(t)+2ξ_jω_j q_j(t)+ω_j^2q_j(t)=-frac{φ_j^TM1}{M_j^*}ẍ_g(t)其中，ω_j=√((K_j)^*)/(M_{j)^*}为第j阶圆频率，ξ_j=frac{C_j^*}{2M_j^*ω_j}为第j阶阻尼比。

1、 工程结构抗震设防的三个水准是什么如何通过两阶段设计方法来实现答：抗震设防的三个水准 ：第一水准：当遭受低于本地区抗震设防烈度的多遇地震影响时，一般不受损坏或不需修理仍可继续使用；第二水准：当遭受相当于本地区抗震设防烈度的地震影响时，可能损坏，经一般修理或不需修理仍可继续使用； 第三水准：当遭受高于本地区抗震设防烈度的罕遇地震影响时，不致倒塌或发生危及生命的严重破坏。

两阶段设计方法：第一阶段设计：对结构和构件进行多遇地震作用下的承载能力验算和弹性变形验算；第二阶段设计：对有明显薄弱层的不规则部位和有特殊要求的结构进行罕遇地震作用下的弹塑性变形验算并采取相应的构造措施。

什么是小震、中震和大震。

答：小震指该地区50年内超越概率约为%的地震烈度，即众值烈度，又称为多遇地震。

中震指该地区50年内超越概率约为10%的地震烈，又称为基本烈度或设防烈度。

大震指该地区50年内超越概率为2%～3%左右的地震烈度，又为称为罕遇地震。

2、 抗震设计中为什么要限制各类结构体系的最大高度和高宽比答：随着多层和高层房屋高度的增加，结构在地震作用以及其他荷载作用下产生的水平位移迅速增大，要求结构的抗侧移刚度必须随之增大。

不同类型的结构体系具有不同的抗侧移刚度，因此具有各自不同的合理使用高度。

房屋的高宽比是对结构刚度、整体稳定、承载能力和经济合理性的宏观控制。

震害表明，房屋高宽比大，地震作用产生的倾覆力矩会造成基础转动，引起上部结构产生较大侧移，影响结构整体稳定。

同时倾覆力矩会在混凝土框架结构两侧柱中引起较大轴力，使构件产生压曲破坏；会在多层砌体房屋墙体的水平截面产生较大的弯曲应力，使其易出现水平裂缝，发生明显的整体弯曲破坏。

3、 简述现行抗震规范计算地震作用所采用的三种计算方法及其适用范围。

答：现行抗震规范计算地震作用所采用的三种计算方法为：底部剪力法，振型分解反应谱法和时程分析法。

适用条件：（1） 高度不超过40米，以剪切变形为主且质量和刚度沿高度分布比较均匀的结构，以及近似于单质点体系的结构，可采用底部剪力法计算。