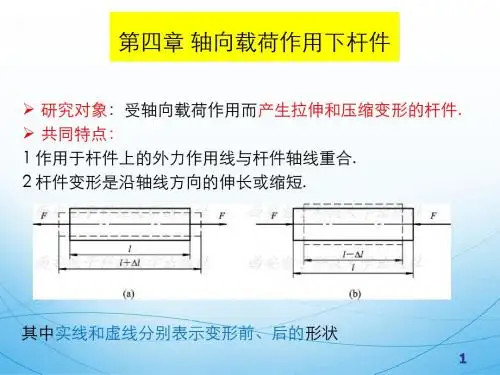
当前位置：文档之家 › 工程力学-第四章

工程力学-第四章

  • 格式：ppt
  • 大小：2.11 MB
  • 文档页数：51

下载文档原格式

  / 51

合集下载

工程力学 第四章 静力学

工程力学 第四章 静力学
§ 4 平面任意力系
各个力的作用线在同一平面内， 但不汇交于一点，也不都平行的力系称 为平面任意力系。
W
2
§4 平面任意力系
平面一般力系实例
3
§ 4-1 力的平移
力的平移定理： 作用于刚体上任意点的力可平移到刚体的任意一点，而不 改变对刚体的作用效应，但需要增加一附加力偶，此附加 力偶的力偶矩矢等于原力对新的作用点之矩矢。
Fx 0 F y 0
几何条件：
FR= 0 或 F =0 力系中各力矢构成的力 多边形自行封闭，或各 力矢的矢量和等于零。
力系中所有各力在两个 坐标轴中每一轴上的投 影的代数和等于零。
21
要注意的问题：
根据题意选择研究对象。 分析研究对象的受力情况，正确地画出其受力图。 研究对象与其他物体相互连接处的约束，按约束 的性质表示约束反力；
M 合力作用线距简化中心 O FR
FR 0 FR 0
MO 0 MO 0 MO 0 MO 0
与简化中心的位置无关 与简化中心的位置无关
16
其中
M d O FR
M o FR, d
FR FR FR
合力矩定理
M o ( FR ) M O M O ( Fi )
q
FC
A
FAx
FC
C
B
FAy
FB
27
2、物体系平衡
物系平衡时，组成该物系的每一个物体，以及 每一个子系统都将处于平衡状态。
整体平衡，局部必然平衡
求解物系平衡问题时要注意的问题：
1、研究对象的选取、受力图 2、外力和内力 3、研究对象的受力图上只画外力不画内力
28
刚体系平衡问题的基本步骤：

工程力学第四章 重心及截面的几何性质

工程力学第四章 重心及截面的几何性质


yC

Wi yi W

zC
Wi zi W

二、均质物体的重心公式 若单位体积的重量γ=常量。以ΔVi表示微小部分Mi的体积，
以V=∑ΔVi表示整个物体的体积，则有 Wi Vi 和W V ，
代入重心公式得：
xC

Vi xi
V

yC

Vi
V
xC

FN Bl W
第二节 截面的几何性质
一、静矩
Sx
ydA
A
,
Sy

xdA
A
静矩可正，可负，可为零，具有长度的三次方量纲。
设该平面图形的形心C的坐标为xC 、yC ，
xc
xdA
A

Sy
AA
,
yc
A ydA S x AA
S x yC A , S y xC A
20
解：（一）组合法 取Oxy坐标系如图所示。
1
单位:mm
2
100
A1 (120 20) 20 2000 mm 2
x1 10 mm
y1

20

120 2
20

70 mm
A2 100 20 2000mm2
x2 50mm y2 10mm
120 20
xC

Ai xi A
第四章
重心及平面图形的几何性质
第一节 第二节
物体重心坐标公式
平面图形的几何性质
本章重点：
计算均质物体的重心坐标。
第一节 重心
重心：物体重力合力的作用点。重心相对于刚体的位置固定不变。

《工程力学》第四章 杆件的应力与强度计算

《工程力学》第四章 杆件的应力与强度计算
3.内力的分布(The distribution of internal force)
正应力均匀分布 F
FN
4.应力的计算公式：
拉压杆横截面上各点处只产生正应力，且正应力在截面上均匀分布 。
F
FN
A
——轴向拉压杆横截面上正应力的计算公式。
FN
式中：
为横截面上的正应力； FN为横截面上的轴力； A为横截面面积。
解:作出砖柱的轴力图 AB段柱横截面上的正应力
BC段柱横截面上的正应力 最大工作应力为
二、轴向拉压杆斜截面上应力的计算
1.斜截面上应力确定
(1) 内力确定：
F
F
FNa= F
(2)应力确定：
F
①应力分布——均布 ②应力公式——
F
a
x
a
FNa
pa FNa
pa
FNa Aa
F A
F cosa cosa
b
问题：正应变是单位长度的线变形量？
三、应力与应变关系(胡克定律 )
一点的应力与该点的应变之间存在对应的关系。
1.单向受力试验表明：在正应力作用下，材料沿应
力作用方向发生正应变，若在弹性范围内加载，正
应力与正应变存在线性成正比：
E ——胡克定律
E 称为材料的弹性模量或杨氏模量。 钢的弹性模量： E 200 GPa 铜的弹性模量： E 120 GPa
直角的改变量。
切应变的特点：
1.切应变为无量纲量;
2.切应变单位为弧度（rad）。
K 3.单元体受力最基本、最简单的两种形式:
单向应力状态：单元体仅在一对互相平行的截面上承受正应力； 纯剪切应力状态：单元体仅承受切应力。
正应变与切应变：

工程力学第4章

工程力学第4章
（３） 列平衡方程，求解未知量。列力矩方程时，通常 选未知力较多的交点为矩心。
（４） 结果分析或校核。
第4章 平面任意力系
例4-2 摇臂吊车如图4-9（a）所示。横梁AB的A端为固定 铰链支座，B端用拉杆BC与立柱相连。已知梁的重力G1＝4kN, 载荷G2＝12 kN，横梁长l＝６ｍ，α＝30°，求当载荷距A端距 离x＝4 ｍ时， 拉杆BC的受力和铰支座A的约束反力。
第4章 平面任意力系
3. 平面力偶系是特殊的力系，根据力偶的性质，在基本方程 中的投影方程自然满足，所以只有一个方程，
MO (F) 0
第4章 平面任意力系
4.2.3
（１） 根据题意，选取适当的研究对象；对所选研究对 象进行受力分析并画受力图。
（２） 选取适当的直角坐标系。坐标轴应与较多的未知 反力平行或垂直。一般情况下，水平和垂直的坐标轴可以不画， 但其它特殊方向的坐标轴必须画出。
第4章 平面任意力系
（3） 该力系上述的三种简化结果，从形式上是不同的， 但都与原力系等效。所以，三种情况的简化结果是等效的。
第4章 平面任意力系
4.1.3 固定端约束
固定端约束是工程中一种常见的约束。如图4-6所示，夹紧 在卡盘上的工件（图(a)），固定在刀架上的车刀（图(b)）， 嵌入墙中的雨罩（图(c)）等都属于固定端约束。由约束的性质 可知， 固定端约束能限制物体沿任何方向的移动，也能限制物 体在约束处的转动。所以，固定端Ａ处的约束反力可用两个正
主矢FR′的大小和方向分别为：
FR' (FRx )2 (FRy )2 2002 1502 250N
tan FRy 150 0.75
FRx 200
第4章 平面任意力系

第四章工程力学

第四章工程力学
13
4.2 横截面上的正应力
1638年：材料力学的开端 《关于两种新科学的对话》
伽利略像
开创了用实验观察——假 设——形成科学理论的方 法
14
研究方法： 实验观察
4.2 横截面上的正应力
作出假设
理论分析
实验验证
1、实验观察
F
a a b b
c c
F
d d
变形前： ab // cd
变形后： ab / /cd
22
低碳钢的拉伸试验
4.3 常温静载下材料的力学性能
试验原理：将试件两端安装在试验机的夹具中，然后缓慢加
载，试件逐渐伸长，直至拉断为止。记下一系列载荷 F 的数
值和与它对应的工作段的伸长量ΔL值。
23
4.3 常温静载下材料的力学性能
低碳钢的拉伸试验
拉伸图（F—ΔL曲线）：以ΔL为横坐标、F为纵
坐标，万能试验机上附有自动绘图设备。
F—ΔL曲线不能反映材料的力学性能：F与ΔL的
对应关系与试件尺寸L有关。
σ—ε曲线（应力—应变曲线）：以F/A=σ作为 纵坐标、ΔL/L=ε作为横坐标。
σ—ε曲线与试件的尺寸无关，反映材料本身的
力学性能。
σ—ε曲线应与F—ΔL曲线相似：A及L均为常数。
– 3kN
9
例 1：图(a)所示杆件在A、C、D三处受力，B处为固定端约束。试求此杆各段的
轴力，并绘出轴力图。
解 ：分别计算AC、CD、DB段的轴力。
AC段：取左段为研究对象，设其上轴力为正 方向。AC段的轴力为 FN1 = F(拉力)
CD段：取左段为研究对象，设其上轴力为正方 向。CD 段的轴力为 FN2=－2F (压力)

工程力学第4章 力系的平衡

工程力学第4章 力系的平衡

2
即空间一般力系平衡的解析条件是力系中所有各力 在任一轴上投影的代数和为零，同时力系中各力对任一 轴力矩的代数和为零。式（4.2）称为空间一般力系的平 衡方程（equationsofequilibrium ofthreedimensionalforcesystem inspace）。 应当指出，由空间一般力系平衡的解析条件可知， 在实际应用平衡方程时，所选各投影轴不必一定正交， 且所选各力矩轴也不必一定与投影轴重合。此外，还可 用力矩方程取代投影方程，但独立平衡方程总数仍然是 6个。
30
4.3.1 有主次之分物体系统的平衡 有主次之分的物体系统，其荷载传递规律是：作用 在主要部分上的荷载，不传递给相应的次要部分，也不 传递给与它无关的其他主要部分；而作用在次要部分上 的荷载，一定要传递给与它相关的主要部分。
31
32
据此，先分析次要部分BD，其受力图如图4.11（b） 所示。建立图示参考系Oxy，列平衡方程并求解。由于 本题只要求出D处的约束反力，而不必要求出B处的约 束反力，故
12
13
建立参考系 Bxy，列平衡方程，求未知力。
14
15
例4.ቤተ መጻሕፍቲ ባይዱ 图4.5所示为一管道支架，其上搁有管道，设 每一支架所承受的管重G1=12kN，G2=7kN，且架重不计。 求支座A和C处的约束反力，尺寸如图所示。
16
17
解 取刚架AB为研究对象，其上所受力有：已知的 集中力F、集度为q的均布荷载，集中力偶；未知的3个 约束反力FAx，FAy，MA。刚架AB的受力图如图4.6（b） 所示。各力组成一平面一般力系。建立图示Oxy坐标系， 列平衡方程求解
9
2.平面一般力系平衡方程的其他形式 （1）二矩式平衡方程

工程力学-第4章

工程力学-第4章

关于材料的基本假定
各向同性假定
关于材料的基本假定
各向同性与各向异性
微观各向异性，宏观各向同性； 微观各向异性，宏观各向异性。
关于材料的基本假定
灰口铸铁的 显微组织
关于材料的基本假定
球墨铸铁的 显微组织
关于材料的基本假定
普通钢材的 显微组织
关于材料的基本假定
若取右段为研究对象，同样可以 确定截面m － m上的剪力与弯矩，所 得的剪力与弯矩数值大小是相同的， 但由于与左段截面m － m上的剪力、 弯矩互为作用与反作用，故方向相反。
FAy
FBy

弹性杆件的外力与内力
截面法
截面法步骤
确定杆件横截面上的内力分量的基本方法—截面法，一般包 含下列步骤： 首先应用工程静力学方法，确定作用在杆件上的所有未知 的外力。 在所要考察的横截面处，用假想截面将杆件截开，分为两 部分。 考察其中任意一部分的平衡，在截面形心处建立合适的直 角坐标系，由平衡方程计算出各个内力分量的大小与方向。 考察另一部分的平衡，以验证所得结果的正确性。

杆件横截面上的应力
正应力与剪应力定义
一般情形下的横截面上的附加分布内力，总可以 分解为两种：作用线垂直于截面的；作用线位于横截 面内的。 分布内力在一点的集度，称为应力(stresses)。 作用线垂直于截面的应力称为正应力(normal stress)， 用希腊字母 表示；作用线位于截面内的应力称为切 应力或剪应力(shrearing stress)，用希腊字母 表示。 应力的单位记号为Pa或MPa，工程上多用MPa。
FR
F3
M

弹性杆件的外力与内力
截面法
内力分量

工程力学第四章

工程力学第四章

代入平衡方程
PPT文档演模板
工程力学第四章
第四章 材料力学概述
PPT文档演模板
材料力学的分析方法
返回首页
工程力学第四章
材料力学的分析方法
分析构件受力后发生的变形，以及由于变 形而产生的内力，需要采用平衡的方法。但 是，采用平衡的方法，只能确定横截面上内 力的合力，并不能确定横截面上各点内力的 大小。研究构件的强度、刚度与稳定性，不 仅需要确定内力的合力，还需要知道内力的 分布。
PPT文档演模板
工程力学第四章
PPT文档演模板
“材料力学”的研究内 容
所谓强度是指构件受力后不发生破坏 或不产生不可恢复的变形的能力；
所谓刚度是指构件受力后不发生超过 工程允许的弹性变形的能力；
所谓稳定性是指构件在压缩载荷的作 用下，保持平衡形式不发生突然转变的能 力（例如细长直杆在轴向压力作用下，当 压力超过一定数值时，在外界扰动下，直 杆会突然从直线平衡形式转变为弯曲的平 衡形式）。
工程力学第四章
“材料力学”的研究内 容
PPT文档演模板
1940年11月，华盛顿州的Tacoma Narrows 桥，由于桥面刚度太差，在42 英里/小时风速 的作用下，产生“Galloping Gertie”(驰振）。
工程力学第四章
“材料力学”的研究内 容
1999年1月4日，我国重庆市綦江县彩虹 桥发生垮塌，造成：
变形前
变形不协调
PPT文档演模板
变形不协调
变形协调一致
工程力学第四章
弹性体受力与变形特征
例题1
图示直杆ACB在两端A、B处固定。关 于其两端的约束力有四种答案。试分析 哪一种答案最合理。
PPT文档演模板

工程力学第4章

工程力学第4章

M Fd M B ( F )
即力向一点平移时所附加力偶的力偶矩 等于原力对平移点之矩。
图4-1
力的平移定理是力系向一点简化的理论依据,它不仅给出了 平移作用于刚体上的一个力的等效条件,而且可直接用来分 析和解决工程实际中的力学问题。
例如,用丝螺纹攻螺纹时,必须两手同时用力,且等值反向。若仅在扳手的 一端作用力F(图4-2a),则这个力与作用在中心处的一个力F'和一个矩为M 的力偶等效(图4-2b),这个力偶使丝螺纹转动,而这个力F'却往往容易使丝 螺纹折断。又如图4-3所示转轴上的齿轮受有周向力F作用,将力F平移至 轴心点O,则力F'使轴弯曲,而矩为M的力偶将使轴产生扭转效应。
图4-2
图4-3
4.2
平面一般力系向作用面内一点简化
设刚体受一个平面力系(F1、F2、…、Fn)作用,现将该力系进行简化。为 简单起见,以三个力F1、F2、F3作用在刚体上(图4-4a)为例说明。在力系 作用平面内任选一点O,将该力系向点O简化,点O称为简化中心。应用 力的平移定理,将各力平移至点O,同时加上相应的附加力偶。这样,原 力系变为作用在点O的平面汇交力系(F' 1、F' 2、F' 3),以及力偶矩为 M1=MO(F1)、M2=MO(F2)、M3=MO(F3)的附加力偶系(图4-4b)。
图4-6
4.3
简化结果分析
平面一般力系向简化中心简化,其主矢F'R和对简化中心的主矩MO 可能有四种情况 1)F'R=0,MO=0 主矢和主矩都等于零。说明简化后的平面汇交力 系和平面力偶系都处于平衡状态,因而原平面一般力系是一个平 衡力系。 2)F'R=0,MO≠0 主矢等于零,主矩不等于零。说明原力系简化为一个 合力偶,其力偶矩等于原力系对简化中心的主矩。若将力系再向其 他简化中心简化,其主矩应等于此合力偶对新简化中心之矩,由力偶 理论知,两者是相同的。说明原力系与一个同平面内的力偶等效。 此时,力系的主矩与简化中心的选择无关。

工程力学第4章

工程力学第4章

外力、内力与截面法
一、外 力
1.外力的定义：外部物体对构件的作用力，称为外 力，包括载荷和约束力。 2.外力的分类：
表面力： 作用在构件表面的外力。
外力
按作用方式
体积力：作用在构件各质点上的外力。
自重、惯性力
集中力 表面力 分布力 集中力
当力作用面积很小，则可将其抽象为 一个点，这时作用力称为集中力。
轴力
弯矩
FN－轴力：产生轴向的伸长或缩短变形；
FQy 或 FQz －剪力：产生剪切变形； Mx－扭矩：产生扭转变形； My或Mz －弯矩:产生弯曲变形。
§ 5-3
外力、内力与截面法
平面一般问题内力分量有几个？ 答：3个。 轴力：FN； 剪力： FQ； 弯矩：M
30
用截面法确定的内力，是截面上分布内力系 的合成结果，它表明该分布力系的分布规律，为 了该研究构件的强度，只知道内力是不够的，比 如，两根不同粗细的杆件，若他们所受的外力相 同，那么横截面上的内力也是相同的。但是，当 外力增大时，细杆先破坏。这是因为横截面面积 小，内力分布的密集程度大的缘故。 应力—分布在内力一点处的集度
三、截面法
F1 F2 F3
F4
假想截面
为求出平衡构件 在外力作用下指定 截面的内力，可以 假想用一个截面将 弹性体在该处截开。
一分为二，每一 部分在截面处存 在一分布内力系。
根据平衡的要求， 每个截开平衡部 分也必须是平衡 的，所以，作用 在每个部分的外 力必须与截面上 分布的力系相平 衡。
F3
材料力学要研究的内力，指在外力的作用下，构 件各部分之间相互作用力因外力而引起的附加值 ，是一种附加内力。
F1 F3
F2
F4
三、截面法

工程力学第四章

工程力学第四章
O O
Z
C
Z
y
a yC
dA
ZC
y
2
ZC
截面对Z轴的惯性矩为：
I Z y dy ( yC a) dy
2 A A
y
yC
IZ
A
2 yC dA 2a
yC dA a A
2 A
截面对形心轴 ZC轴的惯性矩
由ZC轴通过截面 形心，其值为0
2
O
即：I Z I ZC a A
1400 16
50
（2）由平行移轴公式计算惯性矩
Iy
I I I yc 2
(0.24 0.211)m 0.029 m
4
4
0.86m 1.4m3 a A1 (0.7 0.51)2 1.204 m4 z 12 0.24 m 4 A B a b 3 II II 16 16 I yc I y 0 a 2 A2 0.828m 1.334 m yc 12 1.334 ( 0.05 0.51) 2 1.105m 4 c z d 2 y o 4 0.211m C D 430 860
b3
12 0.02m 0.14m3 (0.08 0.0467 )2 m2 2.8 103 m2 12 7.68 106 m4
z A1
2
20
0 100
II
yC
y
140
z
20
II II I yc I y 0 a 2 A2
C
z b 3 2 A2 z 0 12 100 3 (0.01m)(0.02m) 0.0467 mm2 2.0 103 mm2 12
100

工程力学第四章平面一般力系

工程力学第四章平面一般力系
详细描述
平面一般力系简化的目的是将复杂的力系简化为更简单的形式，以便分析刚体的平衡状 态。通过力的平移定理，我们可以将平面一般力系简化为一个合力和一个力矩，或者一 组力和力矩的代数和。这个合力或力和力矩的代数和代表了原力系对刚体的作用效果。
简化后的力系更易于理解和分析，有助于解决工程实际问题。
Part
平衡条件的推导
根据力的平移定理，将平面力系中的所有力平移到同一点， 然后根据合力矩为零和合力为零的条件，推导出平面力系的 平衡条件。
Part
04
平面力系的平衡方程
平衡方程的推导
01
02
03
力的合成与分解
根据力的平行四边形法则， 将力进行合成或分解为多 个分力。
力的投影
将力投影到坐标轴上，得 到力在x轴和y轴上的分量。
STEP 01
分析受力情况
解决静力学问题
利用平衡方程，求解平面 内物体的受力情况，解决 静力学问题。
STEP 03
验证结构稳定性
利用平衡方程，验证结构 的稳定性，确保结构在各 种工况下的安全可靠。
通过平衡方程，分析物体 在平面内的受力情况，判 断物体的运动状态。
Part
03
平面力系的平衡条件
平衡条件的概念
平衡条件是一个物理概念，描述的是物 体在力系作用下保持静止的状态，而平 衡方程是一个数学表达式，用于描述这
一状态。
平衡条件是定性描述，而平衡方程则是 定量描述。平衡方程通过数学符号和运 算，将平衡条件的定性描述转化为可求
解的定量关系。
平衡条件是解决平衡问题的前提，而平 衡方程则是解决问题的工具。通过建立 平衡方程，可以求解未知量，得出物体
平衡条件与平衡方程的联系

工程力学理论力学第4章

工程力学理论力学第4章


Fi xi F
平衡的充要条件为 主矢 R =0
主矩MO =0
所以 平面平行力系的平衡方程为：
Y 0
mO (Fi )0
一矩式
实质上是各力在x 轴上的投影 恒等于零，即 X 0 恒成立 ，所以只有两个 独立方程，只能求解两个独立 的未知数。
mA (Fi ) 0 二矩式
RB


qa 2

m a

2P


200.8 2

16 0.8
22012(
kN)
YA PqaRB 20200.81224(kN)
§4-4 物体系统的平衡、静定与超静定问题的概念
一、静定与超静定问题的概念
我们学过：
平面汇交力系 X 0 Y 0
两个独立方程，只能求两个独立 未知数。
例3. 塔式起重机翻转问题
如图所示塔式起重机的简图。已知机身重W，重 心在C处；最大的起吊重量为P。各部分的尺寸如图。 求能保证起重机不致翻转的平衡锤重Q大小。
b
Q
C e
W
a
P
A
B
dd
★ 物体系统的平衡问题
例5. 如图所示，水平梁由AB和BC两部分组成，它们
在B处用铰链相连。梁的A端固定在墙上，在C处受滚 动支座支持，该支座放在倾角为α =30°的光滑斜面 上。已知P=4KN，均布载荷q=2KN/m，尺寸如图。试求 A、B、C处约束反力。
解物系问题的一般方法：
由整体
局部（常用），由局部
整体（用较少）
[例1] 已知：OA=R, AB= l , 当OA水平时，冲压力为P 时，
求：①M=？②O点的约束反力？③AB杆内力？ ④冲头给导轨的侧压力？

工程力学4第四章弯曲内力

工程力学4第四章弯曲内力

M=±ΣM(Fi)左或右
例1： 已知 q=2 kN / m，求 1-1，2-2，3-3
截面上的内力。
y MA FA
1 1 2m 2 2
q
3
1m 31m
x
1-1 截面：FS = 2×2 = 4 kN，M = -2 ×2 ×3 = - 12 kN.m
2-2 截面：FS = 2×2 = 4 kN， M = -2 ×2 ×1 = - 4 kN.m 3-3 截面：FS = 2×1 = 2 kN， M = -2 ×1 ×0.5 = - 1 kN.m
第四章 弯曲内力
主讲:符春生
§4-1 概述
一、平面弯曲
外力特点:外力是垂直于杆轴线的 力,或作用在包含轴线在 内的平面内力偶。
变形特点:轴线弯成曲线。横截面 轴线
绕垂直于轴线的轴作相 对转动。
轴线
以弯曲为主要变形的杆——梁。
若外力或外力偶作用在纵向对称
面内，杆的轴线在此平面内弯成一平
面曲线——平面弯曲（对称弯曲）。
MA
q0
A
q(x)
B
( 2)
画剪力图和弯矩图
FA
x
l
q0 1 FS ( x) q( x)(l x) (l x)2 2 2l
q0l/2 Fs q0l2/6 +
1 1 q0 M ( x) q( x)(l x) (l x) (l x)3 2 3 6l
M
§4－4剪力、弯矩与荷载集度之间的关系
FS=－FB+F2 ＝ΣFi右
B
M
m
C
F2 FB
FS m
M=FB(l-x)－F2(l-x-b)
＝ΣM(Fi)右

工程力学课件 第四章 平面一般力系

工程力学课件 第四章 平面一般力系

第4章 平面一般力系
14
3. 力系平衡
0, MO 0 FR
FR′
O
MO
合力矩定理 平面一般力系如果有合力，则合力对该力系 作用面内任一点之矩等于力系中各分力对该点之 矩的代数和。
课程：工程力学
第4章 平面一般力系
15
证明： 如下图所示，显然有
M O ( FR ) FR d M O , M O M O ( F ), M O ( FR ) M O ( F )
课程：工程力学
第4章 平面一般力系
1
第4章 平面一般力系
前言 §4-1 力线平移定理 §4-2 平面一般力系向一点简化 §4-3 分布荷载 §4-4 平面一般力系的平衡条件
§4-5 平面平行力系的平衡条件 §4-6 物体系统的平衡问题 §4-7 滑动摩擦
课程：工程力学
第4章 平面一般力系
2
前言
平面一般力系是指位于同一平面内的诸力其作 用线既不汇交于一点，也不互相平行的力系。 工程计算中的很多实际问题都可以简化为平 面一般力系来处理。
FAx A D
B x
arctan
FA y FA x
E F
FAy
P
思考题 4-4 如果例题4-3中的荷载F可以沿AB梁移动，问： 荷载F在什么位置时杆BC所受的拉力（FT）最大？ 其值为多少？
课程：工程力学
第4章 平面一般力系
33
思考题 4-5 (1) 由右图所示的受力图，试按
M A (F ) 0 M B (F ) 0 F
22
(2) 非均布荷载：荷载集度不是常数。 如坝体所受的水压力等。
A qy y
B C
课程：工程力学

工程力学 第四章 杆件的基本变形

工程力学 第四章 杆件的基本变形

随外力产生或消失 随外力改变而改变 但有一定限度
截 面 法
根据空间任意力系的六个平衡方程
X 0 M
步骤： 1、切开 2、代替
x
Y 0 M
y
Z 0 M
z
0
0
0
求内力和取分离体求约束反力的方法本质 相同。这里取出的研究对象不是一个物体系统或一个完 整的物体，而是物体的一部分。
第四章 杆件的基本变形
杆件的外力与变形特点 内力及其截面法
杆件的外力与变形特点
一、杆件变形的定义 杆件在外力作用下，形状和尺寸的变化。 二、杆件变形的形式 1、基本变形 轴向拉伸与压缩 剪切变形 扭转变形 弯曲变形 2、组合变形 同时发生两种或两种以上的变形形式
轴向拉伸或压缩变形
受力特点：作用线与杆轴重合的外力引起的。
拉 伸
压 缩
变形特点：杆轴沿外力方向伸长或缩短， 主要变形是长度的改变
屋 架 结 构 中 的 拉 压 杆
塔 式 结 构 中 的 拉 压 杆
桥 梁 结 构 中 的 拉 杆
剪 切 变形
受力特点：由垂直于杆轴方向的一对大小相等、 方向相反、作用线很近的横向外力引起的。
变形特点：二力之间的横截面产生相对错动变形 主要变形是横截面沿外力作用方向发生相对错动。
螺 栓
连 接 键
销钉
螺 栓
扭 转 变 形
受力特点：由垂直于杆轴线平面内的力偶作用引起的
变形特点：相邻横截面绕杆轴产生相对旋转变形。
对称扳手拧紧镙帽
自 行 车 中 轴 受 扭
桥 体 发 生 扭 转 变 形
弯曲变形
受力特点：是由垂直于杆件轴线的横向力或作用 在杆件的纵向平面内的力偶引起的
变形特点：杆轴由直变弯，杆件的轴线变成曲线。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
15
杆件变形的基本形式
弯曲(bend)
当外加力偶M或外力作用于与杆件垂直的纵向平面内 时，杆件将发生弯曲变形，其轴线将变成曲线。
16
杆件变形的基本形式
组合受力(complex loads and deformation)
由基本受力形式中的两种或两种以上 共同形成的受力与变形形式即为组合受力 与变形。
b
45
应力、应变及其相互关系 应力与应变之间的物性关系
46
应力、应变及其相互关系
σx
x E x ,
x
x
E
O
εx
胡克定律
τ
G ,
O
γ
G
E为弹性模量（杨氏模量），G为切变模量 47
练习题1 • 微元在两种情形下受力后的变形分别如图
（a）和（b）中所示，请根据剪应变的定 义确定两种情形下微元的剪应变。
材料力学课程就是讲授完成这些工作所必 需的基础知识。
19
第四章 材料力学概述
关于材料的基本假定
各向同性与各向异性弹性体 各向同性弹性体的均匀连续性 小变形假定
返回首页
20
关于材料的基本假定
各向同性与各向异性弹性体 在所有方向上均具有相同的物理和力学性能 的材料称为各向同性；否则为各项异性。
材料力学与理论力学在分析方法上不 完全相同。材料力学的分析方法是在实验 基础上，对于问题做一些科学的假定，将 复杂的问题加以简化，从而得到便于工程 应用的理论成果与数学公式。
本章介绍材料力学的基础知识、研究方 法以及材料力学对于工程设计的重要意义。
3
第四章 材料力学概述
“材料力学”的研究内容 杆件的受力与变形形式 工程构件静力学设计的主要内容 关于材料的基本假定 弹性体受力与变形特征 材料力学的分析方法 应力、应变及其相互关系
F1
F3
F2
分布内力
Fn
23
弹性体受力与变形特征
F
F
F
FN=F
弹性体受力后发生的变形还与物性有关。 这表明，受力与变形之间存在确定的关系， 称为物性关系。
24
弹性体受力与变形特征
M0
M0
M0
M＝ M0
25
弹性体受力与变形特征
弹性体受力、变形的第二个特征: 必须满足协调一致的要求。
变形前
变形不协调
43
应力、应变及其相互关 系
正应变与切应变
线变形与剪切变形，这两种变形程 度的度量分别称为“正应变” ( Normal Strain ) 和 “剪应变”(Shearing Strain),
分别用 和 表示。
44
应力、应变及其相互关系
x
x x
x
x
du dx
dx
dx +du
a
a b
( 直角改变量 )
8
“材料力学”的研究内容
1940年11月，华盛顿州的Tacoma Narrows 桥，由于桥面刚度太差，在42 英里/小时风速 的作用下，产生“Galloping Gertie”(驰振）。
9
“材料力学”的研究内容
1999年1月4日，我国重庆市綦江县彩虹 桥发生垮塌，造成：
—— 40人死亡； —— 14人受伤； —— 直接经济损失631万元。
x A xdAz M y
A xdAy M z
FP2
z
41
应力、应变及其相互关系
FP1
y
τxy
剪应力与矩
FQy
τxz dA
FQz
Mx
x
A
xy dA
FQy
A
xz dA
FQz
FP2
z
A xydA z A xzdAy M x
42
应力、应变及其相互关系 应变 —— 各点变形程度的度量
小变形假定 外力作用下，变形与本身几何尺寸相比很小。
各向同性弹性体的均匀连续性 微观不连续 ，宏观连续 。
21
第四章 材料力学概述
弹性体受力与变形特征
返回首页
22
弹性体受力与变形特征
F1
F3
F2
Fn
假想截面
内力与外力平衡； 内力与内力平衡。
弹性体受力、变形 的第一个特征
作用在弹性体上 的外力相互平衡
32
材料力学的分析方法
内力是不可见的，而变形却是可见的，并 且各部分的变形相互协调，变形通过物性关系 与内力相联系。所以，确定内力的分布，除了 考虑平衡，还需要考虑变形协调与物性关系。
对于工程构件，所能观察到的变形，只是 构件外部表面的。内部的变形状况，必须根据 所观察到的表面变形作一些合理的推测，这种 推测通常也称为假定。对于杆状的构件，考察 相距很近的两个横截面之间微段的变形，这种 假定是不难作出的。
在平行于杆横 截面的两个相距很 近的平面内，方向 相对地作用着两个 横向力，当这两个 力相互错动并保持 二者之间的距离不 变时，杆件将产生 剪切变形 。
14
杆件变形的基本形式
扭转(torsion)
当作用在杆件上的力组成作用在垂直于 杆轴平面内的力偶Me时，杆件将产生扭转 变形，即杆件的横截面绕其轴相互转动 。
39
应力、应变及其相互关系
当外力已知时，可由平衡方程求得内 力分量—静定问题。
当内力分量已知时，只能确定应力与 相关内力分量之间的关系，却无法求得各 点应力— 静不定问题。
40
应力、应变及其相互关系
一般情形下，应力与相应内力分量关
系如下：
FP1
y
正应力与矩
My dA
σx
FN x
A
x dA
FNx
FP
ΔlAB ΔlAC 0
B
FP ΔlAB ΔlCB 0
B
B FP /2 ΔlAC ΔlCB
在这三种情形下，AB杆的总变形量都不等于零，
即不满足变形协调的要求，所以是不正确的。
29
弹性体受力与变形特征
第三，力与变形之间的物性关系的概念
l
2l
C
FA
A
F
FP
B
B
ΔlAC ΔlCB
பைடு நூலகம்根据胡克定律，杆的变形与作用在杆上的
力以及杆的长度成正比，即
ΔlAC FNAClAC , ΔlCB FNCBlCB
lCB 2lAC
FNAC 2FNCB
FA 2FB
代入平衡方程
FA FB FP
FA
2 3
FP
,
FB
1 3
FP
30
第四章 材料力学概述
材料力学的分析方法
返回首页
31
材料力学的分析方法
分析构件受力后发生的变形，以及由于变 形而产生的内力，需要采用平衡的方法。但 是，采用平衡的方法，只能确定横截面上内 力的合力，并不能确定横截面上各点内力的 大小。研究构件的强度、刚度与稳定性，不 仅需要确定内力的合力，还需要知道内力的 分布。
4
第四章 材料力学概述
“材料力学”的研究内容
返回首页
5
“材料力学”的研究内 容
材料力学（strength of materials）的研 究内容分属于两个学科。
第一个学科是固体力学(solid mechanics)， 即研究物体在外力作用下的应力、变形和能量， 统称为应力分析（stress analysis）。但是，材 料力学所研究的仅限于杆、轴、梁等物体，其 几何特征是纵向尺寸（长度）远大于横向（横 截面）尺寸，这类物体统称为杆或杆件（bars 或rods）。大多数工程结构的构件或机器的零 部件都可以简化为杆件。
作用线垂直于截面的应力称为正应力
(normal stress)，用希腊字母 表示；作用线
位于截面内的应力称为剪应力或剪应力
(shrearing stress)，用希腊字母表示。应力
的单位记号为Pa或MPa，工程上多用MPa。
36
应力、应变及其相互关系
应力—分布内力在一点的集度
F1 F2
F3
应力就是单位面积上的内力 ?
6
“材料力学”的研究内 容
第二个学科是材料科学中的材料的力学行 为即研究材料在外力和温度作用下所表现出的 力学性能和失效行为。但是，材料力学所研究 的仅限于材料的宏观力学行为，不涉及材料的 微观机理。
以上两方面的结合使材料力学成为工程设计 的重要组成部分，即设计出杆状构件或零部件 的合理形状和尺寸，以保证它们具有足够的强 度、刚度和稳定性。
48
练习题2
➢ 由金属丝弯成的弹性圆
环，直径为d（图中的
实线），受力变形后变
成直径为d+Δd的圆
（图中的虚线）。如果
d 和Δd 都是已知的，
请应用正应变的定义确 定： （1） 圆环直径的相对改 变量； （2） 圆环沿圆周方向的 正应变。
49
练习题3
➢ 微元受力前形状如图中实
线ABCD所示，其中∠ABC 为直角，dx = dy。受力变
7
“材料力学”的研究内容
所谓强度是指构件受力后不发生破坏 或不产生不可恢复的变形的能力；
所谓刚度是指构件受力后不发生超过 工程允许的弹性变形的能力；
所谓稳定性是指构件在压缩载荷的作 用下，保持平衡形式不发生突然转变的能 力（例如细长直杆在轴向压力作用下，当 压力超过一定数值时，在外界扰动下，直 杆会突然从直线平衡形式转变为弯曲的平 衡形式）。
17
第四章 材料力学概述
工程构件静力学设计的主要内容
返回首页
18
工程构件静力学设计的主要内容
为了完成常规的工程设计任务，需要进行 以下几方面的工作：
分析并确定构件所受各种外力的大小和方 向。 研究在外力作用下构件的内部受力、变形和 失效的规律。