当前位置：文档之家 › 科氏加速度.ppt

科氏加速度.ppt

  • 格式：ppt
  • 大小：785.51 KB
  • 文档页数：21

下载文档原格式

  / 21

合集下载

向心加速度及科氏加速度小认识

向心加速度及科氏加速度小认识

向心加速度与科氏加速度小认识向心加速度及与速度方向垂直的速度不改变速度大小只改变方向。

在时间很短的情况下。

向心方向产生一个速度与切向速度合成。

那么久而久之速度就会越来越大啊？答：与速度垂直的加速度，必然是由一个与速度垂直的力产生的，而瞬时位移始终是瞬时速度方向相同的，所以产生垂直加速度（向心加速度）的力始终和瞬时位移垂直。

因此这个力对物体不做功，物体的动能不增加，所以物体的速度不增加。

我觉得只有这样算是比较好理解的，如果一定要用加速度的效果来计算，我猜想可能需要用到求极限或者是求导数的方法，还是向量求极限或求导数，计算会更麻烦的。

科氏加速度认识历史旋转体系中质点的直线运动科里奥利力是以牛顿力学为基础的。

1835年，和提出，为了描述旋转体系的运动，需要在中引入一个假想的，这就是科里奥利力。

引入科里奥利力之后，人们可以像处理中的运动方程一样简单地处理旋转体系中的运动方程，大大简化了旋转体系的处理方式。

由于人类生活的本身就是一个巨大的旋转体系，因而科里奥利力很快在流体运动领域取得了成功的应用。

物理学中的科里奥利力科里奥利力来自于物体运动所具有的，在旋转体系中进行直线运动的，由于惯性的作用，有沿着原有运动方向继续运动的趋势，但是由于体系本身是旋转的，在经历了一段时间的运动之后，体系中质点的位置会有所变化，而它原有的运动趋势的方向，如果以旋转体系的视角去观察，就会发生一定程度的偏离。

如右图所示，当一个质点相对于惯性系做直线运动时，相对于旋转体系，其轨迹是一条曲线。

立足于旋转体系，我们认为有一个力驱使质点运动轨迹形成曲线，这个力就是科里奥利力。

根据的理论，以旋转体系为，这种质点的直线运动偏离原有方向的倾向被归结为一个外加力的作用，这就是科里奥利力。

从的角度考虑，科里奥利力与一样，都不是真实存在的力，而是惯性作用在内的体现。

科里奥利力的计算公式如下:式中为科里奥利力；m为质点的质量；为质点的运动速度；为旋转体系的角速度；表示两个的符号。

科氏加速度PPT课件

科氏加速度PPT课件

垂直于一个平面,这个平面是由V和ω的方向所组成的 平面.所以fc垂直于V, 使V发生偏转.
（２） 傅科摆摆球振幅直径（弧长）公式：
R l g
R是傅科摆摆球振幅直径（摆球重力沿圆弧切线方向在振幅相等的 时间走过的空间弧长在地面的投影长度），l 是指傅科摆吊索的长 度，g是指重力加速度，
圆周的周长公式： L 2R
Fc=2m V × ω。
傅科摆是科里奥利力的一个重要应用。
傅科摆
（１）用科里奥利力解析傅科摆
Hale Waihona Puke 下面用科里奥利力向大家详细介绍一下有关傅科摆的问题。
上面已经说明，在一般情况下，科里奥利力的公式为：
fc=2mv×ω
w : 转动系的角速度矢量，w的方向与转轴重合，指向按右手螺旋法则
规定。
傅科摆受科里奥利力解释对于北半球Ａ点的傅科摆来讲，当摆在一
在转动参考系内 作匀速运动的质 点，除受惯性离 心力个，还受另 一种虚拟力——
科里奥利力。
科里奥利 1792---1843
引例
我们先从一个简单的例子说起。如图： 设在以角速度ω沿逆时针方向转动的水 平圆盘上，有A，B两点，O为圆盘中心， 且有OA>OB，在A点以相对于圆盘的速度 V沿半径方向向B点抛出一球。如果圆盘 是静止的，则经过一段时间
柏而定律图示
2.大气环流：大气运动的能量来源于太阳辐射， 气压梯度力是大气运动的源动力。全球共有赤道 低压带，南、北半球纬度30°附近的副热带高压 带，南、北半球纬度60°附近的副极地低压带， 南、北半球的极地高压带等七个气压带。气压带 之间在气压梯度力和地转偏向力的作用下形成了 低纬环流圈、中纬环流圈和高纬环流圈。由于受 地转偏向力的作用，南北向的气流却发生了东西 向的偏转。北半球地面附近自北向南的气流，有 朝西的偏向。在气压带之间形成了六个风带，即 南、北半球的低纬信风带，南、北半球的中纬西 风带，南、北半球的极地东风带。
柯氏加速度

柯氏加速度


v r '−v r 2 = 2 sin
⋅ vr '
方向与 vr 垂直，并与 ω
vr '−vr 2
一致
∆t → 0, − → 2 2 2 转向一致。
π ∆ϕ
π
(2) lim ∆t →0
v e '−v e ∆t
v e '−v e = (v e '− v M 1 ) + (v M 1 − v e )
ve '−ve ve '−vM1 vM1 −ve lim = lim +lim ∆t→ 0 ∆t→ 0 ∆t ∆t ∆t→0 ∆t
v r '−v r a r = lim ∆t →0 ∆t
?
v e '−v e ae = lim ∆t →0 ∆t
?
(1) lim ∆t →0
v r '−v r ∆t
v r '− v r = (v r '− v r 2 ) + (v r 2 − v r )
v '−v v '−v v −v lim r r = lim r r2 +lim r2 r ∆t→ 0 ∆t ∆t→0 ∆t ∆t→0 ∆t
其中
a e = lim ∆t → 0
v M1 − v e ∆t
第一项 大小：
ve ' = ω ' ⋅ AM ' , vM 1 = ω ' ⋅ AM 1
ve − ve
'
ve
'
vM 1 − ve
ve − vM 1
'
ve
vM 1
AM '− AM 1 v e '−v M 1 = ω ⋅ lim = v rω lim ∆t → 0 ∆t → 0 ∆t ∆t
科氏加速度

科氏加速度

运动员起跑
田径比赛，比如中长跑项目中。运动员都是沿着逆时针方向 跑动的。这样 做的奥秘就在于地球自转所引起的科氏效应。地球做自西向东的自转，角速 度 方向指向北方。按科氏理论．在北半球的田径场上。运动员的 科氏加速 度的水平分量指向左侧，科氏力水平分量指向右侧。根 据作用力与反作用 力规律，地面将给运动员一个方向向左的作用 力，所以运动员向左转弯比 较省力。
ห้องสมุดไป่ตู้
逆螺旋
留心生活的人不难发现打开放水塞．水池里的水流漩涡总是 逆时 针的，在天气预报节目中卫星云图中的气旋也是逆时针的。 这也 是科氏效应的一种。在地里学中，科氏力通常被称为地转偏 向力。 在北半球，科里奥利力使风向右偏离其原始的路线；在南半 球， 这种力使风向左偏离。风速越大，产生的偏离越大。于是，在 北 半球，当空气向低压中心辐合时会向右弯曲，形成了一个逆时 针 方向的旋转气流。从高压中心辐散出来的空气，则因为向右弯 曲 而形成了顺时针方向的旋风。我们把逆时针旋转的叫做气旋， 把 顺时针旋转的叫做反气旋。在南半球。上述的情形则正好相反。 我 们可以推测出科里奥利效应在极地最显著，向赤道方向逐渐减 弱 直到消失在赤道处。这就是为什么龙卷风可以通过赤道，但很 难 在赤道附近引发龙卷风。
对科氏力与科氏加速度的理解(WLEI)

对科氏力与科氏加速度的理解(WLEI)

对科氏力与科氏加速度的理解从字面意思来看，一般人很容易认为科氏力是导致科氏加速度的原因，然而这却是一个十分错误的理解。

实际上科氏力与科氏加速度本质上是没有联系的，如果硬说有联系，也无非是二者的方向恰好相反而已。

下面我将对这两个概念进行具体阐述。

科氏力：科氏力是一种本质上不存在的力，就像离心力一样，没有施力物体。

它的提出主要是为了说明一种运动现象，以便于对该运动进行分析和计算。

那么科氏力要说明的一种运动现象是什么样的呢？假设一个旋转的圆盘在做定轴转动，圆盘上的一个小球在惯性空间中作直线运动，那么小球的运动相对于圆盘坐标系就是在做曲线运动，则在圆盘坐标系里为了解释这种曲线运动是如何产生的，于是便引入了科氏力的概念。

设小球的质量为m ，惯性空间速度为V ，圆盘转速为ω，则科氏力可表示为 =2()F m V ω⋅⨯科括号内表示V 与ω的矢量积，方向按右手坐标系判定。

科氏加速度：科氏加速度是由于作直线运动的物体同时又做牵连的旋转运动而产生的。

科氏加速度本质上也没有施力物体，引入科氏加速度主要是为了解释在惯性空间坐标系里的物体运动方向和大小发生改变的现象。

设物体相对于旋转体运动速度为r V ，牵连转速为ω，那么科氏加速度可表示为=2r a V ω⨯科，方向按右手坐标系判定。

科氏力与科氏加速度的区别：（1） 二者适用的坐标系不同：科氏力适用于旋转体坐标系，而科氏加速度适用于惯性空间坐标系。

（2） 二者所用变量不同：科氏力公式中的线速度V ，是相对于惯性空间坐标系的；而科氏加速度公式中的r V ，是相对于旋转体坐标系的。

（3） 二者的公式中矢量积的两个变量的位置是相反的，故导致了方向的相反。

相关物理现象分析：1）、北半球河流的右岸比左岸侵蚀的严重：由于地球本身自转，故其就类似于一个旋转体，河流中河水类似于旋转体上小球。

在旋转坐标系中，采取科氏力的概念，由于地球是两极略扁的球体，故在北半球可近似认为旋转角速度方向指向天空，根据右手定则，科氏力的方向总在河流流向的右侧，即在科氏力的作用下，河水对右岸的冲击力比左岸的大，所以北半球河流右岸侵蚀严重。

机构速度和加速度分析的一般图解法

机构速度和加速度分析的一般图解法

选已知参数较多的点一般为铰链点为此有时应将构件扩大至所选取的重合点1列矢量方程并分析各矢量2选取适当比例尺按方程作速度多边形及加速度多边形图3根据作图求解4科氏加速度存在的条件32用图解法作机构的运动分析用图解法作机构的运动分析23232323科氏加速度存在的条件科氏加速度存在的条件当两构件构成移动副若移动方向无转动分量即只作平动时无科氏加速度
§3-2 用图解法作机构的运动分析
1.矢量方程图解法
（1）矢量方程图解法的基本原理 理论力学中的运动合成原理 （2）矢量方程图解法的作法 在对机构进行速度和加速度分析时，首先根据运动合成原理 列出机构运动的矢量方程，然后再按方程作图求解 两构件以转动副相连时，在转动副中心处具有相同的速度和
加速度，两构件以移动副相连时，两构件具有相同的角速度和角
加速度
§3-2 用图解法作机构的运动分析
（3）矢量图的画法
D A B C
大小：？ √ √ 方向：？ √ √ √ √
D A B C
大小：√ 方向：√ ？ ？ √ √ √ √
B A
D
B
C
A
D
C
§3-2 用图解法作机构的运动分析
D A B C
加速度存在的条件
当两构件构成移动副，若移动方向无转动分量即只作平动时， 无科氏加速度； 当两构件构成移动副，若移动方向含有转动分量时，存在断
科氏加速度 3
2 2 3 2
2 3
3
大小：√ ？√√
方向：√ √ ？
？
方向：√ √ ？ √
B
B
A D
C
A D
C
§3-2 用图解法作机构的运动分析
2.利用同一构件上两点间的速度和加速度矢量方程作图求解
科氏加速度与科氏惯性力实验

科氏加速度与科氏惯性力实验

科氏加速度与科氏惯性力实验在一般情况下，牛顿定律只能应用于惯性坐标系，因此，在工程实际中都假定地球是静止不动的。

而实际上，即使不考虑地球每年绕太阳一周的公转运动，地球也还有每昼夜自转一周的自转运动，这就使得当考虑地球自转的影响时，运动的物体除受到重力的作用外，还将受到另一种力的作用，即科氏惯性力的作用。

本实验就是为了验证科氏惯性力的存在而设计的。

一、实验目的观察科氏惯性力的存在现象，了解产生科氏加速度的原因。

实验对象圆盘皮带轮上的皮带二、实验仪器及工作原理1. 实验仪器 科氏惯性力演示仪2. 工作原理科氏惯性力主要是由坐标系的转动与物体在动坐标系中的相对运动引起的，具体表达式为()r e c g v m a m F ⨯-=⋅-=ω2，式中g F 表示科氏惯性力，m 表示运动物体的质量，c a 表示科氏加速度，e ω表示坐标系转动的牵连角速度，r v 表示物体相对于动坐标系的相对运动速度。

科氏惯性力演示仪就是利用上述原理设计的。

首先在固定支架上建立了一个可转动的圆盘，此圆盘转速定，但可以改变转动方向。

圆盘上装有两个小电机，并由皮带相连接，通过按动不同的按钮，电机可改变转速和转动的方向。

设动坐标系与圆盘相固连，e ω就是圆盘的转动角速度，皮带在小电机的带动下所作的运动为相对运动，r v 就是皮带的相对运动速度。

（1）当圆盘转动而皮带不动时，虽然有动坐标系的转动而没有相对运动，此时没有科氏惯性力产生。

（2）当圆盘不转动而皮带作直线运动时，因只有相对运动而没有动坐标系的转动，此时也没有科氏惯性力产生。

（3）当圆盘转动，同时皮带也作直线运动时，由于动坐标系的转动和动点在动坐标系上的相对运动，即产生了科氏惯性力，它促使皮带向中间靠拢或分开 (它决定于e ω、r ω的方向)。

（4）改变相对运动速度的大小和方向，可以改变皮带向中间靠拢或分开的大小。

四、实验步骤1．仔细检查仪器的设置状态，皮带在圆盘上的位置，打开电源总开关。

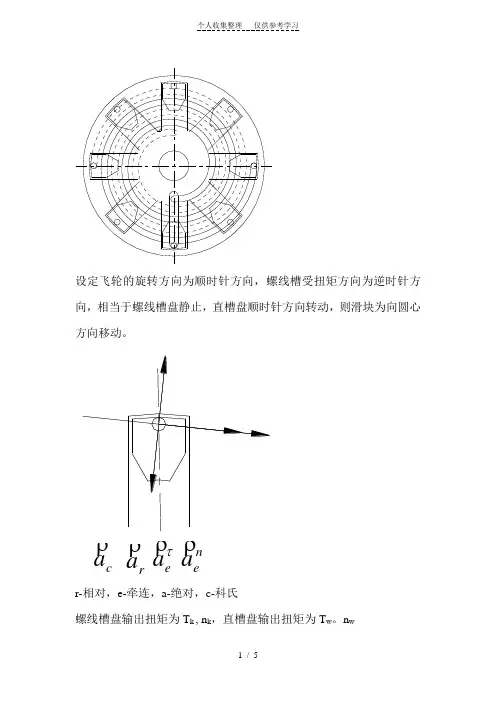
力学分析内容_科氏加速度

力学分析内容_科氏加速度

设定飞轮的旋转方向为顺时针方向，螺线槽受扭矩方向为逆时针方向，相当于螺线槽盘静止，直槽盘顺时针方向转动，则滑块为向圆心方向移动。

c a r a e a n e ar-相对，e-牵连，a-绝对，c-科氏 螺线槽盘输出扭矩为T k , n k ，直槽盘输出扭矩为T w 。

n w动点：滑块上的轴圆心动系：螺线槽圆盘绝对运动：曲线运动相对运动：螺线槽切向运动牵连运动：定轴转动c n e e r a a a a a a 1111 +++=τr a 1 ，相对运动为动点相对于螺线槽切向的角速度，不考虑径向的加速度，其大小和直槽盘该点的角加速和螺线槽盘改点的角加速度差值与半径的乘积在切线上的投影，即和β角有关，所以)tan cos()(cos )(1θααβααa r r a slot spiral slot spiral r ⋅-⋅=⋅-⋅= 方向为切线方向τe a 1 即为螺线槽盘的角加速度与半径的乘积，s p ie r a ατ⋅=1 n e a 1 即为向心加速度，21spiral n e r a ω⋅=c a 1 为)tan cos()(22θωωωωa r v slot spiral spiral r e ⋅-⋅⋅⋅=⋅⋅ 方向即为图示方向动点：滑块上的轴圆心动系：直槽圆盘绝对运动：曲线运动相对运动：径向直线运动牵连运动：定轴转动c n e e r a a a a a a +++=τr a 和半径的缩小速度有关有关，半径的公式为θa r =，所以r a 的大小和r 有关，即和θ a 有关，而θ 即为螺线盘的角减速度和直槽盘角减速度的差值，用slot spiral αα-表示，即)(slot spiral r a a αα-⋅= ，方向如图所示，指向圆心。

τe a 为牵连切向加速度，显然为直槽盘的角加速度和半径的乘积，即为slot r α⋅，方向为切向 τe a 为牵连径向加速度，公式为2slot r ω，方向指向圆心 c a 为科氏加速度，大小为)(222slot spiral slot spiral slot slot r e a a v ωωωθωω-⋅⋅⋅=⋅⋅⋅=⋅⋅- 方向为切向。

科式加速度

科式加速度

相对加速度取决于相对运动轨迹的形状，
如果是曲线，那就分法向和切向；
如果是直线，那就只有切向
牵连加速度取决于牵连运动的形式，转动还是平动
科氏加速度的方向一般可将相对速度沿角速度W
的方向旋转九十度得到。

对于相对、牵连加速度中，法相加速度不可随便画！
而未知的切向加速度可以随便画
科氏加速度方向判断:右手螺旋定则，
首先伸出右手四指弯曲的方向与角速度w相同，
大拇指所指的方向为角速度w的矢量方向，
然后用右手伸直的四指指向角速度的的方向与速度差乘，此时大拇指指向即为科氏加速度方向.。

科氏效应与科氏加速度

科氏效应与科氏加速度

科氏效应和科氏加速度科氏效应最初由法国的气象学家科里奥利在1835年在论文上进行理论描述，并提出科氏力的概念。

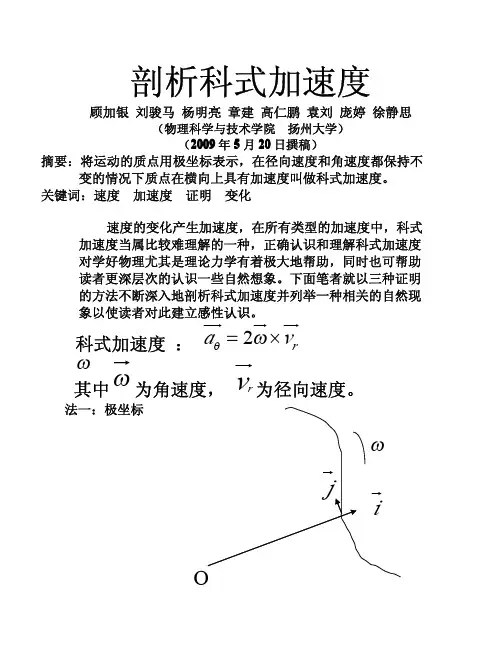
一下通过建立双坐标系向量空间来阐述科氏力和科氏加速度的推导。

如图所示，O’X’Y’Z’为旋转坐标系，它绕惯性坐标系OXYZ的Z轴进行转动，令旋转坐标系瞬时角速度为ω，瞬时角加速度为ε，并假设动点M在旋转坐标系中作相对运动。

根据动点运动的向量合成定理，动点M的绝对速度为：v a=v r+ v e（2-1）其中v a为动点M的绝对速度，v r为动点M相对于旋转坐标系的相对速度，v e为动点M的牵连速度。

对式（2-1）进行一阶求导，可得动点M的绝对加速度为：a a=dv rdt + dv edt（2-2）其中a a为动点M的绝对加速度。

此外动点M的牵连速度和牵连加速度由以下两式可分别进行表征：v e=ω×r(2-3)a e=ε×r+ ω×v e(2-4) 其中r为动坐标系相对于惯性坐标系的径向速度，a e为M的牵连加速度。

对动点M 的牵连速度进行求导，可以得到一个牵连加速度的合成式，如下式所示：dv e dt =dωdt×drdt=ε×r+ ω×v e+ ω×v r=a e+ ω×v r另外，当对M的相对速度求导可得以下合成结果：dv r=a r+ ω×v r其中a r为M点的相对加速度。

将式（2-5）和（2-7）代入式（2-2）得到完整的M点绝对加速度公式：a a=dv rdt + dv edt=a r+ a e+2ω×v r(2-7)令：a k=2ω×v r则式（2-7）可以写成：a a=a r+ a e+ a k其中a k被称为后人根据克里奥立名字命名的科氏加速度，当其作用在质量上便形成了所谓的科氏力。

通过前面的论述可知，当物体的牵连运动为转动时，物体的牵连运动必要与物体的相对运动的互相作用，使物体本身具有除了绝对加速度和相对加速度这两个分量外的另一个分量——科氏加速度分量。

剖析科氏加速度

剖析科氏加速度


�� � vr
�、�两个加速度大小相等，方向 相同。 所以科式加速度（横向方向上的加速度）为：
�� � �� �� � aθ = 2ω × vr
通过以上分析我们可以得知，科式加速度是由两部分组 分，即径向速度方向变化和横向速度大小变化。初学者往往 只能分析其一，而不能综合考虑，所以不知道系数“2”是怎 么回事。 其实方法一和方法三是统一的，只不过方法一侧重于数 学上的逻辑推理，而方法三侧重物理上的发散思维分析。
= 2ω vr
（ aθ 即为科式加速度）
法三：分析法 若能求出质点在径向速度和角速度都保持不变的情况下 运动的横向加速度，那么求出的这个加速度即为科式加速 度。
要想求出质点横向方向上的加速度，就先得通过分析知 道在这个方向上速度的变化量，在用速度变化量对时间求微 商，求出来的即为科式加速度。 质点的速度可以分解为径向速度和横向速度，下面将分 别分析这两个速度在横向方向上的变化量。（此时我们很自 然地知道，对横向速度分析大小变化，而对径向速度分析方 向变化。） 对横向速度（大小）进行分析
�� � �� �� � 科式加速度 ： aθ = 2ω × vr ω
其中
法一：极坐标
ω 为角速度， vr 为径向速度。
� j
ω
� i
O
� � � d ρ i dρ � � dr � di d ρ � v= = = i+ρ = i + ρω j dt dt dt dt dt
� � r = ρi
( )
� � � dv d 2 ρ � d ρ � d ρω j a= = 2 i+ ω j+ dt dt dt dt � 2 � � � � d ρ dρ dρ dω dj = 2 i+ ωj+ ωj+ρ j + ρω dt dt dt dt dt � � d 2ρ � d ρ � d ρ � = 2 i+ ωj+ ω j + ρβ j − ρω 2 i dt dt dt � � d 2ρ � d ρ � 2 = 2 i+2 ω j + ρβ j − ρω i dt dt

科氏加速度

加速度合成定理
1
加速度合成定理
i y j z k va x
' i ' y ' j ' z ' k ' vr x
aa ae ar
z
？
i j k aa x y z
' i ' ' j ' ar x y z' k '
B
解：动点： 杆上A点 动系： 滑块 运动分析 绝对运动： 直线运动
相对运动： 圆周运动
vr
va

u
ve
r
牵连运动： 直线平移
速度分析： va
ve vr
a
A
va ve tan u tan ve u vr cos cos
12
加速度分析： a B
a
ae ar aC
ro'
◎
' i ' y ' j ' z ' k ' ) d vr d( x dt dt x ' i ' y ' j ' z ' k ' x ' i ' y ' j ' z ' k '


o x
d r' dt
r y'
y
ωe r ' vr
x ' i ' y ' j ' z ' k ' e x ' i ' y ' j ' z ' k '
ar

对科氏加速度的认识

对科⽒加速度的认识对科⽒加速度的认识内容摘要：本⽂先简介了科⾥奥利其⼈，交代了科⽒加速度的发现过程，⼜从不同⽅⾯解释了科⽒加速度。

通过⼀些常见的⽣活常识及⽣产应⽤的举例，说明了科⾥奥利加速度的普遍性和意义。

⼀．科学家的发现科⾥奥利，法国物理学家。

1792年5⽉21⽇⽣于巴黎；1843年9⽉19⽇卒于巴黎。

科⾥奥利是巴黎⼯艺学院的教师，长期健康状况不佳，这限制了他创造能⼒的发挥。

即便如此，他的名字在物理学中仍是不可磨灭的。

1835年，他着⼿从数学上和实验上研究⾃旋表⾯上的运动问题。

地球每24⼩时⾃转⼀周。

⾚道⾯上的⼀点，在此时间内必须运⾏25，000英⾥，因此每⼩时⼤约向东运⾏1，000英⾥。

在纽约纬度地⾯上的⼀点，⼀天只需⾏进19，000英⾥，向东运⾏的速度仅约为每⼩时800英⾥。

由⾚道向北流动的空⽓，保持其较快的速度，因此相对于它下⾯运动较慢的地⾯⽽⾔会向东⾏。

⽔流的情况也是⼀样。

因此，空⽓和⽔在背向⾚道流动时好像被推向东运动，反之会向西运动,这样会形成⼀个圆!推动它们运动的⼒就称为科⾥奥利⼒。

这种⼒不是真实存在的!只是"惯性"这种性质的表现⽽已.正是这种"⼒"造成了飓风和龙卷风的旋转运动。

研究⼤炮射击、卫星发射等技术问题时，必须考虑到这种⼒。

⼆．科⽒加速度的定义科⽒加速度----是动点的转动与动点相对运动相互耦合引起的加速度。

科⽒加速度的⽅向垂直于⾓速度⽮量和相对速度⽮量。

A.理论解读物理上，“有⼒就产⽣加速度，相反有加速度就会有产⽣它的⼒”这句话，是在“惯性参照系”当中来说的。

⽽科⽒⼒（或科⽒加速度）是在⾮惯性系当中的概念。

所以它的本质上还是⼀种惯性⼒，是参照系本⾝施加给它的。

B.形象理解⽤2维的⽅式⽐较容易理解些。

设想，你坐在⼀个圆盘上，但并不知道它在转动。

这时有个球从圆⼼开始向外移动，并且圆盘和球之间⽆摩擦，这时从外⾯的参照系看球应该⾛直线，但是你坐在圆盘上看，球就在不断往⼀个⽅向弯了。

科氏加速度与科氏惯性力实验

科氏加速度与科氏惯性力实验在一般情况下，牛顿定律只能应用于惯性坐标系，因此，在工程实际中都假定地球是静止不动的。

而实际上，即使不考虑地球每年绕太阳一周的公转运动，地球也还有每昼夜自转一周的自转运动，这就使得当考虑地球自转的影响时，运动的物体除受到重力的作用外，还将受到另一种力的作用，即科氏惯性力的作用。

本实验就是为了验证科氏惯性力的存在而设计的。

一、实验目的观察科氏惯性力的存在现象，了解产生科氏加速度的原因。

实验对象圆盘皮带轮上的皮带二、实验仪器及工作原理1. 实验仪器科氏惯性力演示仪2. 工作原理科氏惯性力主要是由坐标系的转动与物体在动坐标系中的相对运动引起的，具体表达式为，，F,,m,a,,m2,，v，式中F表示科氏惯性力， gcergm表示运动物体的质量，a表示科氏加速度，,表示ec坐标系转动的牵连角速度，表示物体相对于动坐标vr系的相对运动速度。

科氏惯性力演示仪就是利用上述原理设计的。

首先在固定支架上建立了一个可转动的圆盘，此圆盘转速定，但可以改变转动方向。

圆盘上装有两个小电机，并由皮带相连接，通过按动不同的按钮，电机可改变转速和转动的方向。

设动坐,标系与圆盘相固连，就是圆盘的转动角速度，皮带在小电机的带动下所作的e v运动为相对运动，就是皮带的相对运动速度。

r(1)当圆盘转动而皮带不动时，虽然有动坐标系的转动而没有相对运动，此时没有科氏惯性力产生。

(2)当圆盘不转动而皮带作直线运动时，因只有相对运动而没有动坐标系的转动，此时也没有科氏惯性力产生。

(3)当圆盘转动，同时皮带也作直线运动时，由于动坐标系的转动和动点在动坐标系上的相对运动，即产生了科氏惯性力，它促使皮带向中间靠拢或分开 (它决定于、的方向)。

,,er(4)改变相对运动速度的大小和方向，可以改变皮带向中间靠拢或分开的大小。

四、实验步骤1(仔细检查仪器的设置状态，皮带在圆盘上的位置，打开电源总开关。

2(设置只有动坐标系的转动而没有相对运动的状况，观察皮带中点的位置。

科氏加速度(by self)


回顾科氏加速度
在瞬时t 在瞬时t’
va vr ve v a ' v r ' v e '
经过 t
v a v a 'v a (v r 'v r ) (v e 'v e )
aa
v a v e 'v e v r 'v r lim lim lim t 0 t t 0 t 0 t t
v r 'v r 2 2 sin
大小： v r ' v r 2
vr '
方向：与 v r 'v r 2 一致 t 0, 2 2 2 方向与 v r 垂直，并与 转向一致。
( 2) lim0 t
v e 'v e t
v e 'v e (v e 'v M 1 ) (v M 1 v e )
va ve vr
M2
B
va ve
M
B
vr
M
M1
A
A
即：动点在某一瞬时的绝对速度等于它在该 瞬时的牵连速度与相对速度的矢量和。这就 是点的速度合成定理。
牵连运动为平动时 点的加速度合成定理
aa ae ar
基本形式
即：当牵连运动为平动时，动点在某瞬时的绝对加速 度等于该瞬时它的牵连加速度与相对加速度的矢量和。 这就是牵连运动为平动时点的加速度合成定理。
ve 've ve 'v M 1 v M 1 ve lim0 lim0 lim0 t t t t t t
其中
a e lim0 t
v M1 v e t
第一项 大小：

科氏加速度公式

科氏加速度公式科氏加速度公式是一种测量系统的加速度的方法，是一种重要的物理原理。

该公式可以用于表达物体加速过程中的加速度。

它定义了一个物体从一个速度到另一个速度所需要时间的公式。

可以用简单的数学公式来描述它：加速度（a）= 化速度（v）/化时间（t）加速度（a）是物体速度每秒的变化量，代表的是物体的变速率。

比如一辆汽车从静止开始加速，加速度是描述汽车每秒速度增加的量，即6米每秒/秒，即6米每秒的变化量就是6米的加速度。

变化速度（v）是物体在一段时间内变化的速度，也就是物体从一点到另一点所经过的时间。

比如前面的汽车，如果从0开始加速，到达60米每秒，那么这段时间内，汽车的变化速度就是60米每秒。

变化时间（t）是描述物体加速过程中所经过时间的一个参数，比如汽车加速到60米每秒，那么这段加速过程所用时间就是变化时间。

科氏加速度公式主要用于测量物体加速过程的物理学原理，它是一种简单的物理学原理，它只需要时间和速度的变化量就可以表达物理原理。

然而，科氏加速度公式不仅仅可以用来测量物体的加速度，它还可以用来测量物体的减速度。

减速度是指物体每秒速度减少的量，也就是物体每秒减速的量。

比如一辆车从某个速度减速到静止，减速度就是这种每秒速度减少的量，即6米每秒/秒就是6米的减速度。

所以，科氏加速度公式也可以用来测量物体减速的物理原理。

科氏加速度公式的应用非常广泛，它可以用来分析物体在加速或减速过程中的物理原理，也可以用来验证一些受力相关的物理模型。

比如在航空航天、航天科学以及地震学中，科氏加速度公式都得到了广泛的应用，在科学研究中可以用来表达物体受力和加速度、减速度的变化关系。

此外，科氏加速度公式在实际生活中也有着重要的用途。

比如，在制造工业中，它可以用来测量机械设备加速、减速过程中的加速度和减速度的变化量，为设备的高效运行提供有力的保证。

此外，它还可以用来测量在许多汽车安全设备中，汽车在加速或减速过程中的安全性，以确保汽车的安全。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

利用此例可导出科里奥利力的定量公式。 以转动系为参考系，球从A到 达B’的时间是
△t’=（OA－OB）/V’
在△t’时间内球偏离AB的距离
BB’=（V1－V2）△t’
=ω（OA－OB）△t’
= V’ω t'2
在△t’很小的情况下，可以认为沿BB’的运动是匀加速运动而初速为0，以
a’表示以加速度应用BB’=1/2 a’ t'2，与上一结果比较可得：a’=2V’ω。
（２） 傅科摆摆球振幅直径（弧长）公式：
R l g
R是傅科摆摆球振幅直径（摆球重力沿圆弧切线方向在振幅相等的 时间走过的空间弧长在地面的投影长度），l 是指傅科摆吊索的长 度，g是指重力加速度，
圆周的周长公式： L 2R
综合以上公式可以得出: L 2R 2 l g
平均每周角的周长公式：
在此转动参考C=ma’=2m V’ω
在此例中，圆盘沿逆时针方向转动，科里奥利力方向指向质点运动的右 方。同理，如果圆盘沿顺时针方向转动，则科里奥利力的方向指向质点 运动的左方。
一般地可以证明，当质量为m的质点相对 于转动参考系（角速度矢量为ω ）的速 度为V时，则在转动参考系内观察到的科 里奥利力为
B B‘ O
A
对于以圆盘为参考系的B，他只看到A以初速度向他 抛来一球，但球并未沿直线到达他，而是向球球运 动的前方的右侧偏去了，这一结果的分析发现，地 球在具有径向初速度V’的同时，还具有了垂直于这 一方向而向右的加速度a’，应用牛顿第二定律对于加 速度的解释，既然球出手后在水平方向上没有受到 “真实力”的作用，那么球一定受到了一个垂直于 速度V’而向右的惯性力Fc。这种在转动参考系中观 察到的运动物体（由于转动参考系中各点的线速度 不同而产生）的加速现象中科里奥利效应，产生此 效应的虚拟的惯性力叫科里奥利力。
则小球受到的科里奥利力为：
fc = fc r + fΦ (3)
并且该力肯定会在这样的一个平面上, 这个平面是由V 和ω的方向所组成的平面,并且与速度V垂直.
如果对V整体来分析,因为V不与Z轴平行,所以必 受科里奥利力的作用.其所受科里奥利力fc 的方向垂 直于一个平面,这个平面是由V和ω的方向所组成的平 面.所以fc垂直于V, 使V发生偏转.
1.柏而定律：该定律是自然地理中一条著名的、从 实际观察总结出来的规律，即北半球河流右岸比较陡 削，南半球则左岸比较陡削。这可以由地转偏向力得 到说明，北半球河水在地转偏向力作用下，对右央求 冲刷甚于左岸，长期积累的结果，右岸比较陡峭。
地球自转引起水流的科氏惯性力，水流的科氏惯性力冲刷河流 右岸（北半球）．
柏而定律图示
2.大气环流：大气运动的能量来源于太阳辐射， 气压梯度力是大气运动的源动力。全球共有赤道 低压带，南、北半球纬度30°附近的副热带高压 带，南、北半球纬度60°附近的副极地低压带， 南、北半球的极地高压带等七个气压带。气压带 之间在气压梯度力和地转偏向力的作用下形成了 低纬环流圈、中纬环流圈和高纬环流圈。由于受 地转偏向力的作用，南北向的气流却发生了东西 向的偏转。北半球地面附近自北向南的气流，有 朝西的偏向。在气压带之间形成了六个风带，即 南、北半球的低纬信风带，南、北半球的中纬西 风带，南、北半球的极地东风带。
？科里奥利力在地球上有哪些表现？
下面介绍一些现实生活中受科里奥利力影响形成 的现象：
我国地处北半球，物体在地面上运动，受地转偏 向力作用而自行向右偏转，这种现象在日常生活中还 从来没有观察到。人在走路时，也从来不会不自觉地 偏到右边去。这完全是因为地转偏向力很小，其效应 被其他作用力的效应所掩盖。地转偏向力的效应只有 在长时间累积的条件下，才容易察觉。
Fc=2m V × ω。
傅科摆是科里奥利力的一个重要应用。
傅科摆 （１）用科里奥利力解析傅科摆 下面用科里奥利力向大家详细介绍一下有关傅科摆的问题。
上面已经说明，在一般情况下，科里奥利力的公式为： fc=2mv×ω
w : 转动系的角速度矢量，w的方向与转轴重合，指向按右手螺旋法则 规定。
傅科摆受科里奥利力解释对于北半球Ａ点的傅科摆来讲，当摆在一 Ａ点有任意速度Ｖ时，其速度均可分为三个分量，径向分量Ｖr ，角向 分量ＶΦ ，轴向分量V//。 对于Ｖr ：根据公式，可知其受到的科里奥利力为：fc r = 2mvr ×ω, 其大小为2mvrω , 方向为沿y 轴正方向． 对于ＶΦ ：则根据分式有，fΦ ＝２mvΦ×ω , 其大小为2mvΦω ,方向 为沿x轴的正方向． 对于V// ：因为V// 与ω的方向夹角为0，所以其不受科里奥利力的作用。
△t=（OA－OB）/V
后，球会到达B，但结果是球到达了B 转动的前方一点B’，对这个现象可如下 分析，由于圆盘在转动，故球离开A的 时，除了具有径向速度V’外，还具有切 向速度V1，而B的切向速度为V2，由于 B的位置靠近圆心，所以V1＞V2，在垂 直于AB的方向上，球运动得比B远些。
这是在盘外不转动的惯性系观察到 的情形。
L°
L 360°
2 l g 360°
L是指傅科摆摆球振幅圈的总周长，是指傅科摆摆球振幅圈总周长
的平均周角度的平均周长．
傅科摆的圆周角是360°角，一天的时间是24小时，那么傅科摆每
小时的振幅圆周角是15°角。每小时有60分钟，那么每分钟的振幅
圆周角是0.25°角。
地球是一个转动参考系，在地球 上运动的物 体也受科里奥利力作用．
关于科里奥利力
PB04203141 朱坤战
在转动参考系内 作匀速运动的质 点，除受惯性离 心力个，还受另 一种虚拟力——
科里奥利力。
科里奥利 1792---1843
引例
我们先从一个简单的例子说起。如图： 设在以角速度ω沿逆时针方向转动的水 平圆盘上，有A，B两点，O为圆盘中心， 且有OA>OB，在A点以相对于圆盘的速 度V沿半径方向向B点抛出一球。如果 圆盘是静止的，则经过一段时间
大气环流
3.气旋和反气旋：气旋与反气旋是大气中最常见 的运动形式，也是影响天气变化的重要天气系统。在 气压梯度力和地转偏向力的共同作用下，大气并不是 径直对准低气压中心流动，也不是沿辐射方向从高气 压中心流出。低气压的气流在北半球向右偏转成按逆 时针方向流动的大旋涡，在南半球向左转成按顺时针 方向流动的大旋涡，大气的这种流动很象江河海流中 水的旋涡，所以又叫气旋。夏秋季节，在我国东南沿 海经常出现的台风，就是热带气旋强烈发展的一种形 式。高气压的气流在北半球按顺时针方向旋转流出， 在南北半球按逆时针方向旋转流出，高气压的这种环 流系统叫反气旋。